Hom-Hopf代數上的L-R smash積
鄭乃峰, 孔翔
(1.寧波大學理學院,浙江 寧波 315211;2.寧波工程學院理學院,浙江 寧波 315211)
Hom-Hopf代數上的L-R smash積
鄭乃峰1, 孔翔2
(1.寧波大學理學院,浙江 寧波 315211;2.寧波工程學院理學院,浙江 寧波 315211)
在Hom-Hopf代數上,定義了L-R smash積概念并討論了它的相關性質,給出了L-R smash積是Hom-Hopf代數的充要條件.
Hom-Hopf代數;L-R smash積;Hom-雙模代數
1 引言
Hom-代數的概念是由Makhlouf和Silvestrov于 2006年在研究擬李代數時引入的[1]. Hom-代數推廣了結合代數,把結合代數中的結合性法則作了形變,將其變成了線性變換α結合性條件,即α(a)(bc)=(ab)α(c).隨著Hom-代數研究的深入,一些學者在文獻[2-4]中又陸續引入了Hom-余結合余代數、Hom-雙代數和Hom-Hopf代數等,給出了一些重要的結論.
Smash積是Hopf代數理論中的重要概念之一,近年來,人們對其做了各種形式的推廣.如文獻[5]給出了一種新的Smash積,使Smash積和交叉積均是它的特例;而文獻[6-7]分別給出了Hopf代數和擬Hopf代數的L-R smash積的概念.本文利用Hom-雙模代數,構造了Hom-Hopf代數上的L-R smash積,并給出了L-R smash積是Hom-Hopf代數的充要條件.
本文的所有工作都是在域k上進行的.所討論的模、張量積和線性映射均指域k上的.文中將使用Sweedler關于余代數余乘法的記號
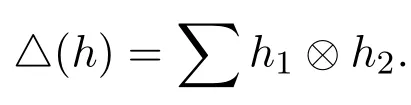
S(或SH)表示Hom-Hopf代數H的對極映射.
2 L-R smash積
關于Hom-代數、Hom-余代數及Hom-Hopf代數的概念和性質,可參閱文獻[1-4,8-9].本節先介紹Hom-模代數和Hom-雙模代數的概念,后構造Hom-Hopf代數上的L-R smash積,并給出L-R smash積是Hom-Hopf代數的充要條件.
設(H,β)是Hom-雙代數,(A,α)是Hom-代數.如果有一個線性映射
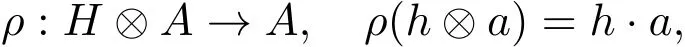
使下面條件成立:
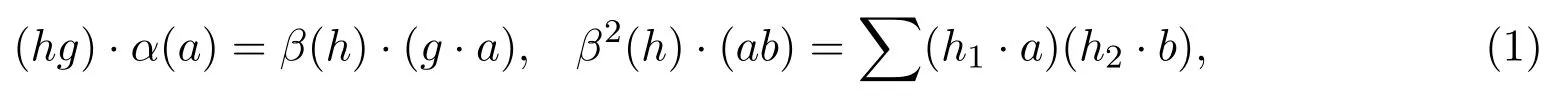
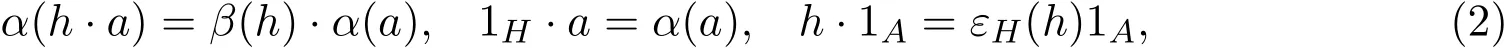
則稱(A,α)是左H-模Hom-代數.同理可定義右H-模Hom-代數.若(A,α)既是左H-模Hom-代數又是右H-模Hom-代數,且滿足下式:

則稱(A,α)是H-雙模Hom-代數.
定義2.1設(H,β)是Hom-雙代數,(A,α)是H-雙模Hom-代數.令線性映射
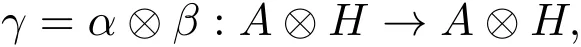
在張量空間A?H上有一個代數結構,稱為L-R smash積,記作(A?H,γ),對任意a,b∈A, h,g∈H,其乘法運算規定如下:
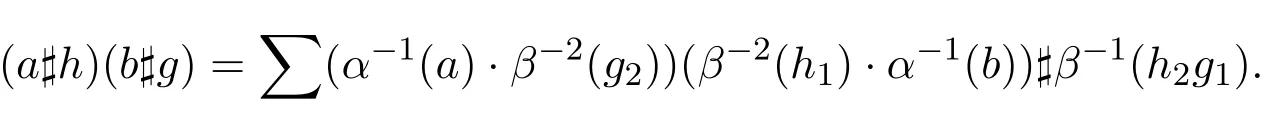
則有如下結論.
定理2.1設L-R smash積(A?H,γ)的定義如上,則(A?H,γ)是以1A?1H為單位元的Hom-代數.
證明對任意a,b,c∈A和h,g,k∈H,直接計算,有
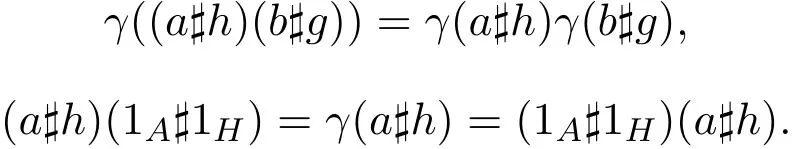
下面證明(A?H,γ)滿足Hom-結合律.
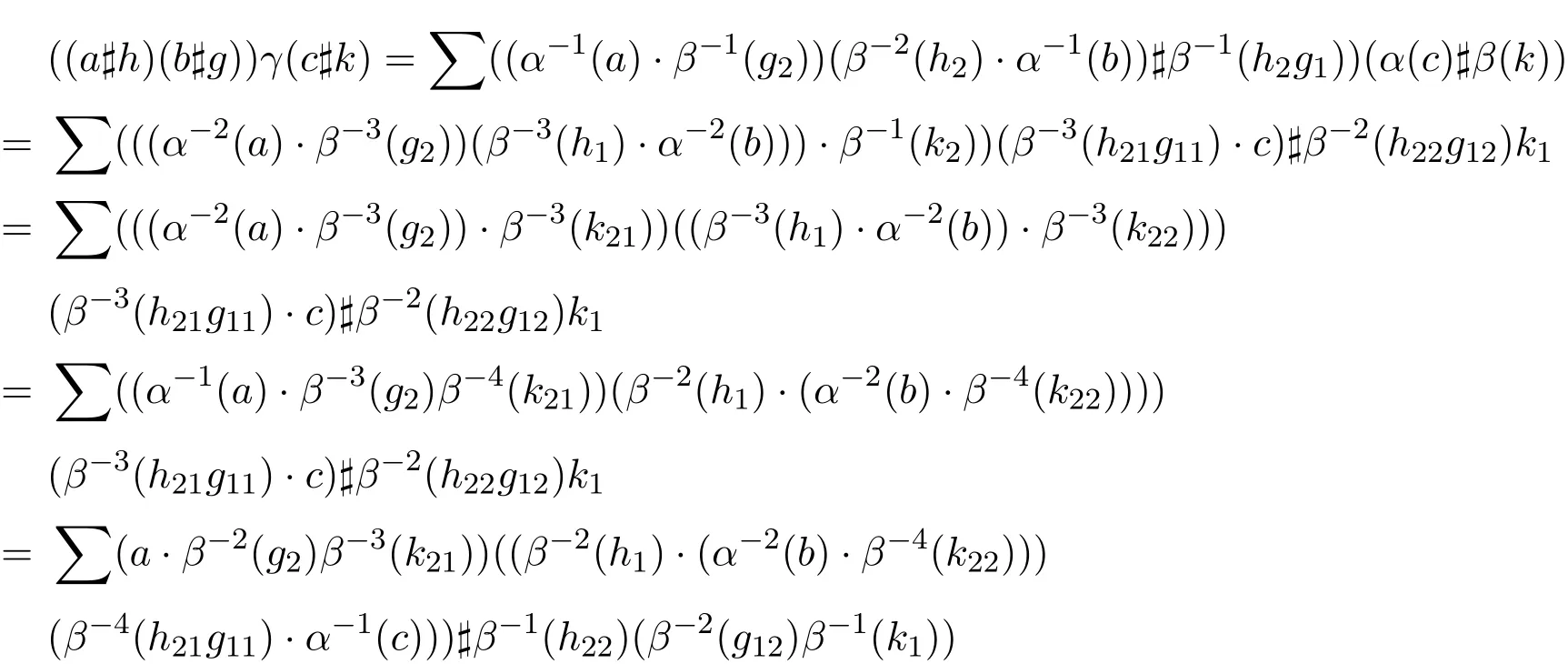
即L-R smash積(A?H,γ)是一個Hom-代數.
注2.1如果α和β是恒等映射,即對任意的a∈A和h∈H,有則L-R smash積(A?H,γ)是文獻[6-7]中的L-R smash積.如果Hom-代數(A,α)的右H-模作用是平凡的,則L-R smash積(A?H,γ)是Hom-代數上的smash積.
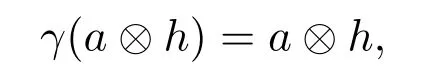
引理2.1設(A?H,γ)為L-R smash積,則對任意a,b∈A和h,g∈H,下面關系式成立:

證明直接驗證可得.
下面給出L-R smash積(A?H,γ)是Hom-雙代數的充要條件.
定理2.2設A,H是Hom-雙代數,則L-R smash積(A?H,γ)是Hom-雙代數,當且僅當對任意的h∈H,a∈A,下列條件成立:

其中(A?H,γ)的余代數結構是Hom-張量積余代數,其余乘和余單位定義為:
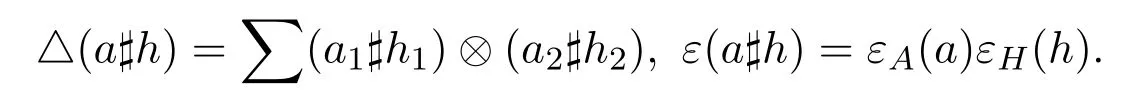
進一步地,如果(A,α)和(H,β)是Hom-Hopf代數,其對極映射分別為SA和SH,則(A?H,γ)也是Hom-Hopf代數,其對極映射S為:
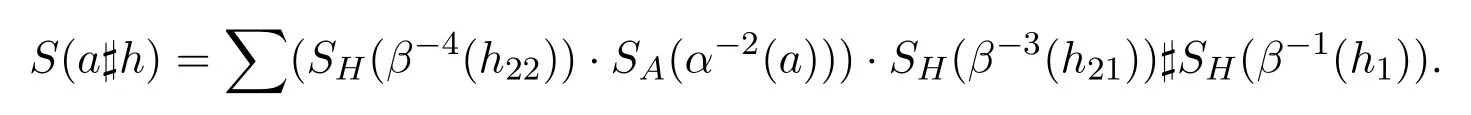
證明ε是Hom-代數同態當且僅當(4)式成立,直接驗證即可.下面證明△是Hom-代數同態當且僅當(5)-(7)式成立.設a,b∈A和h,g∈H,有
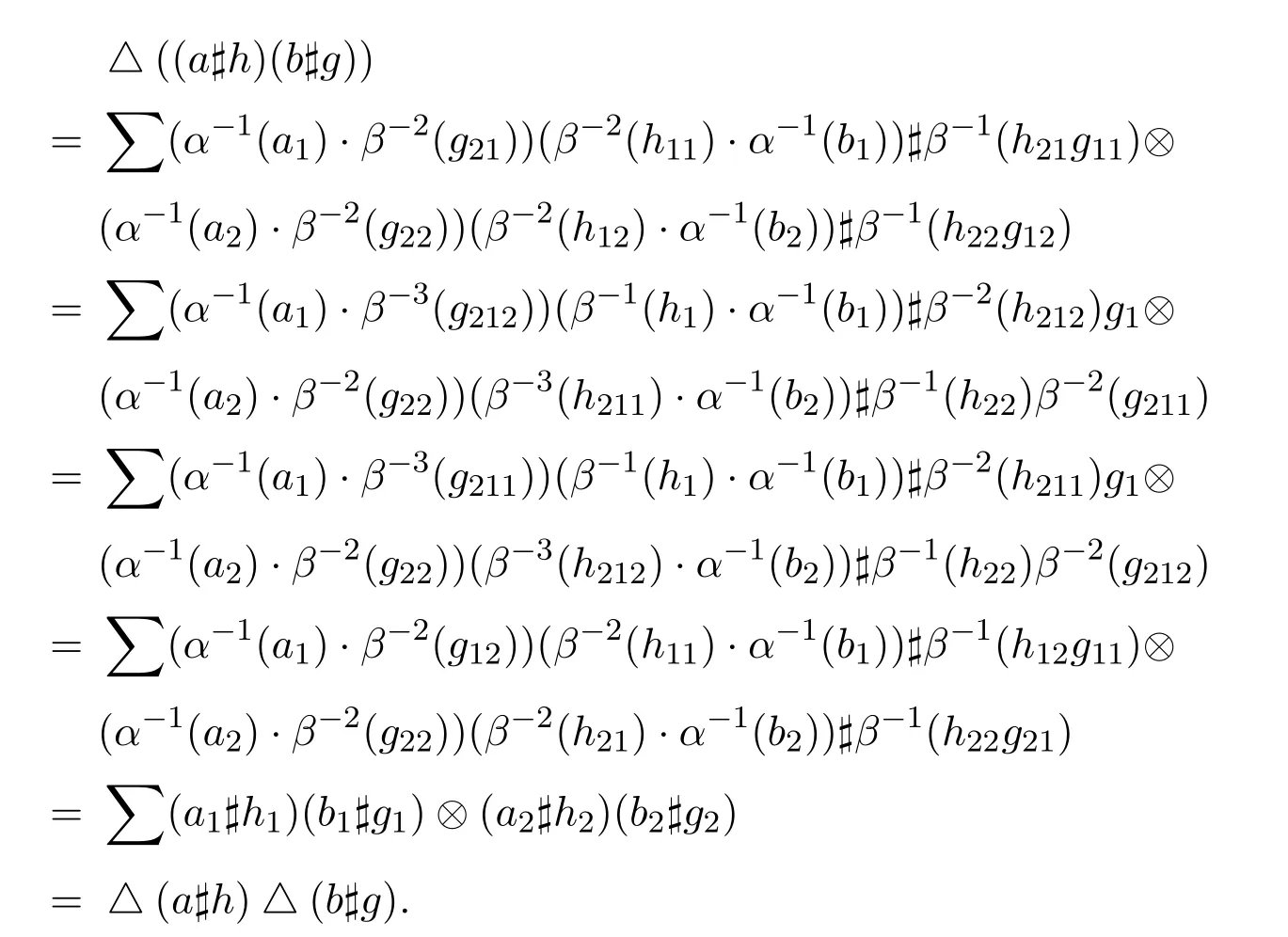
反之,如果△是Hom-代數同態,則由等式
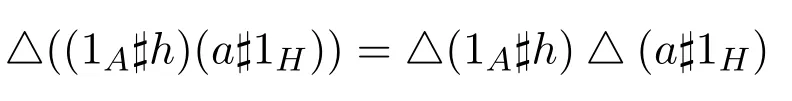
展開可得:
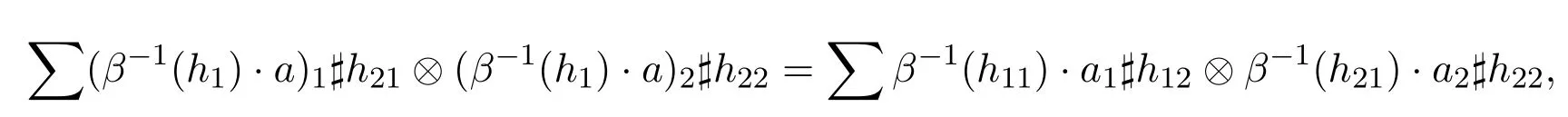
把IA?εH?IA?εH作用于上式兩端,可得條件(5)的前一式成立.把εA?IH?IA?εH作用于上式兩端,可得條件(6)成立.
由等式
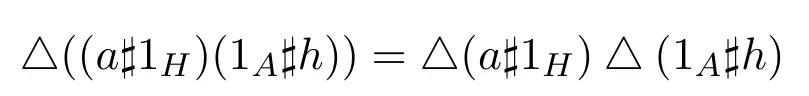
展開可得:
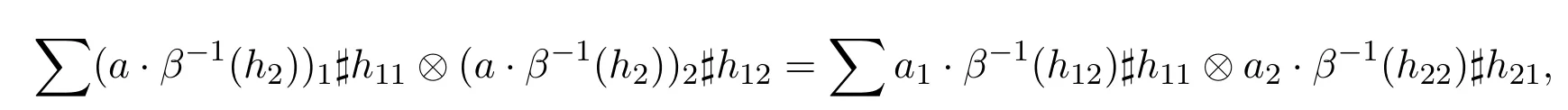
把IA?εH?IA?εH作用于上式兩端,可得條件(5)的后一式成立.把IA?εH?εA?IH作用于上式兩端,可得條件(7)成立.
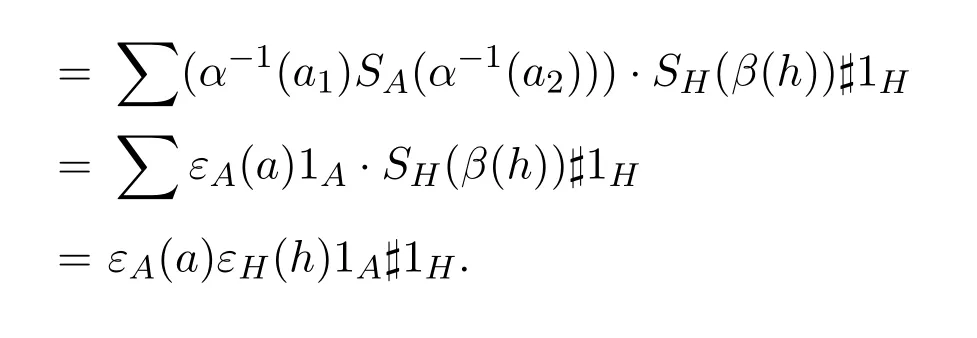
同理可證
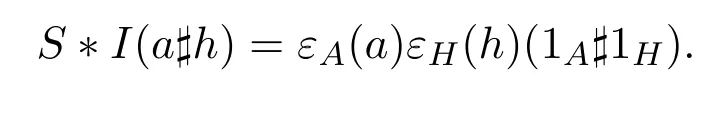
因此,(A?H,γ)是Hom-Hopf代數.
[1] Makhlouf A,Silvestrov S.Hom-algebras structures[J].J.Gen.Lie Theory Appl.,2008,2:51-64.
[2] Makhlouf A,Silvestrov S.Hom-algebras and Hom-coalgebras[J].J.Alg.Appl.,2010,9:553-589.
[3] Caenepeel S,Goyvaerts I.Monoidal Hom-Hopf algebras[J].Comm.Alg.,2011,39:2216-2240.
[4] Yau D.Hom-bialgebras and comodule Hom-algebras[J].Inter.Elect.J.Alg.,2010,8:45-64.
[5] 鄭乃峰.(ω,σ)-Smash積和(υ,α)-Smash余積[J].純粹數學與應用數學,2012,28(2):167-175.
[6] Zhang L Y.L-R smash products for bimodule algebras[J].Prog.Natu.Scie.,2006,166:580-587.
[7] Panaite F,Oystaeyen F V.L-R smash product for(quasi)Hopf algebras[J].J.Algebra,2007,309(1):168-189.
[8] Yau D.Hom-quantum groups I:quasi-triangular Hom-bialgebras[J].arXiv:0912.4128.
[9] Zheng N F.The quasi-triangular structures of Hom-ω-smash product Hopf algebra[J].Chinese Annals of Mathematics,2013,34A(6):689-708.
L-R smash product for Hom-Hopf algebras
Zheng Naifeng1,Kong Xiang2
(1.Faculty of Science,Ningbo University,Ningbo 315211,China;
2.Faculty of Science,Ningbo University of technology,Ningbo 315211,China)
In this paper,we give the concept of L-R smash product over Hom-Hopf algebras and investigate their properties.In addition,the necessary and sufficient conditions for(A?H,γ)to be Hom-Hopf algebra are given.
Hom-Hopf algebra,L-R smash product,Hom-bimodule algebra
O153.3
A
1008-5513(2014)04-0354-06
10.3969/j.issn.1008-5513.2014.04.004
2014-03-23.
鄭乃峰(1968-),副教授,研究方向:Hopf代數及量子群.
2010 MSC:16W30

