改進的二維最小卡方散度圖像分割方法

王晨，樊養余，熊磊

1.西北工業大學電子信息學院，西安 710072

2.空軍工程大學航空航天工程學院，西安 710038

改進的二維最小卡方散度圖像分割方法

王晨1，2，樊養余1，熊磊2

1.西北工業大學電子信息學院，西安 710072

2.空軍工程大學航空航天工程學院，西安 710038

1 引言

圖像分割作為圖像分析和圖像理解的基礎，其性能關系到圖像處理任務的成敗，因此是圖像處理領域研究的重要內容之一[1-3]。然而由于自然界的復雜性，目前還沒有一種較為通用的圖像分割技術。針對不同應用背景，相關研究人員先后提出了種類繁多的圖像分割方法。在這些方法中，基于圖像直方圖信息的閾值化方法由于它的簡潔有效性得到了眾多研究人員的青睞[4]。在圖像閾值化方法中，最為經典的方法如Otsu提出的最大類間方差法[5]、最小誤差閾值化[6]、基于圖像熵的方法[7-9]等。由于熵方法有著堅實的物理學背景，因此在圖像處理領域得到了成功的關注。在熵方法中有一類稱為交叉熵的方法是該類方法的一個強力分支，在圖像閾值化分割中得到了成功的應用[10-12]。

但是，交叉熵閾值法因存在對數運算，導致其計算量較大，不便于許多實時場合的廣泛應用。本文引入卡方散度來度量兩個概率分布的差異程度，提出了新的基于卡方散度的圖像閾值化分割準則。實驗結果表明，基于卡方散度的圖像閾值化分割準則是可行的，且計算所需時間量比交叉熵值法有了明顯的減少。因此，在實時性要求較高的場合比較適宜。另外，基于卡方散度的閾值化分割方法在處理受到噪聲干擾的圖像時，可以比交叉熵法獲得更好的分割結果。

2 基于卡方散度的分割方法

交叉熵[10]，又稱為相對熵或有向散度，用來度量兩概率向量之間差異性。卡方散度[13]也可以用來度量兩個概率分布的差異性程度。因此，本文將卡方散度用于圖像閾值化問題。

2.1 卡方散度

在交叉熵的求取過程中含有對數運算，其計算量大，不利于實時性要求高的場合。本文利用卡方散度來度量兩個概率分布間的差異程度[12-13]：

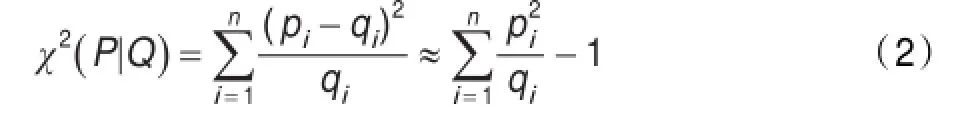
文獻[12]說明了簡單的基于卡方散度的圖像分割會出現較多錯分部分，丟失一部分圖像原有的有用信息。因此本文提出一種基于改進的卡方散度的圖像分割方法。

2.2 基于對稱卡方散度的閾值化原理

設I是大小為M×N，灰度級為L的數字圖像，I={f(x，y)|x∈{1，2，…，M}，y∈{1，2，…，N}，f(x，y)表示圖像坐標(x，y)處的像素值。圖像的歸一化直方圖可表示為H={h0，h1，….，hL-1}，且0≤hi≤1。

圖像進行閾值分割時，假設t是分割閾值，t把圖像分割為兩部分，其中灰度級{0，1，…，t}的像素值表示背景，{t+1，t+2，…，L-1}表示目標。

對于卡方散度而言，一般χ2(P|Q)不具有對稱性，因此定義它的對稱版本為：

在式（3）的基礎上，本文構造了一種更為有效的圖像閾值化方法。為了敘述方便，首先令：

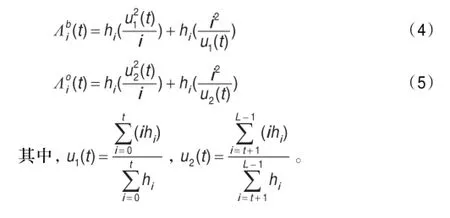
把式（4）、（5）代入式（3），可以得到關于圖像閾值化前后背景與目標的散度，即

定義閾值化前后圖像總的散度為：

要獲得最佳閾值，可對式（7）求極小值，即

其中t*表示最佳閾值。求出t*后，可用下式對原圖像進行閾值化：

其中，f(x，y)、f′(x，y)分別表示原始圖像、閾值圖像坐標(x，y)處的像素值。

2.3 計算復雜性分析

假設計算機每次執行加法（減法）運算一次所需時間（單位：s）為t1，執行一次乘法或除法運算所需時間（單位：s）為t2，且t1＜t2。文獻[14]中詳細分析了原始卡方散度與交叉熵的計算復雜性。因此，本文計算其對稱卡方散度J(P|Q)所用的時間（單位：s）為4nt2+2(n-1)t1+t1。

所以，交叉熵比對稱卡方散度的計算多花費時間（單位：s）為：(4kn+2n-1)t1+(k2n+4kn)t2。

3 改進的二維卡方散度分割方法

3.1 二維直方圖的構建

假設一幅圖像大小為M×N，灰度級為L，用f(x，y)表示原始圖像，g(x，y)表示原始圖像的均值濾波結果。設l(i，j)表示f(x，y)中灰度級為i且g(x，y)中灰度級為j的像素對個數，那么定義二元組(i，j)在圖像和其鄰域濾波圖像中出現的聯合概率：

其中，i=0，1，…，L-1;j=0，1，…，L-1。以上就是在二維直方圖構建中出現最多的一種構建方法，即均值二維直方圖[15]，它是一個L×L的矩陣，如圖1（a）所示。其中區域1和2代表目標和背景，區域3和4表示邊緣點及噪聲。

由于圖像的均值濾波屬于一種平滑處理，即低通濾波方式，一般被用來處理高斯噪聲。均值濾波在平滑圖像得到鄰域平均灰度的同時，使圖像變得模糊，而且濾波效果不佳，尤其對椒鹽噪聲濾波效果不如中值濾波。中值濾波法[1]則是一種非線性平滑技術，它是通過從圖像中的某個采樣窗口取出n個數據進行排序，然后用排序后的中值取代要處理的數據來實現抑制圖像噪聲的目的。這種方法在濾除噪聲點的同時能夠較好地保存圖像的細節和邊緣。

中值濾波和均值濾波通常被分別用來處理脈沖噪聲和高斯噪聲，當圖像同時存在高斯噪聲和脈沖噪聲時，單獨用哪種濾波方法都不會達到好的去噪效果。因此，本文選擇文獻[16]中采用的改進中值濾波方法對圖像進行濾波，然后再利用濾波圖像和原始圖像構建新的二維直方圖。

令w(x，y)表示新的原始圖像濾波結果，又令g(x，y)= |f(x，y)-w(x，y)|，本文構建了如圖1（b）所示的新的中值二維直方圖。這種構建方法不僅使區域1，區域2盡可能地包含了所有目標點和背景點，同時也避免了常用的均值二維直方圖及其區域劃分方法中區域1和區域2可能存在邊緣點和噪聲點導致分割結果不準確的問題。

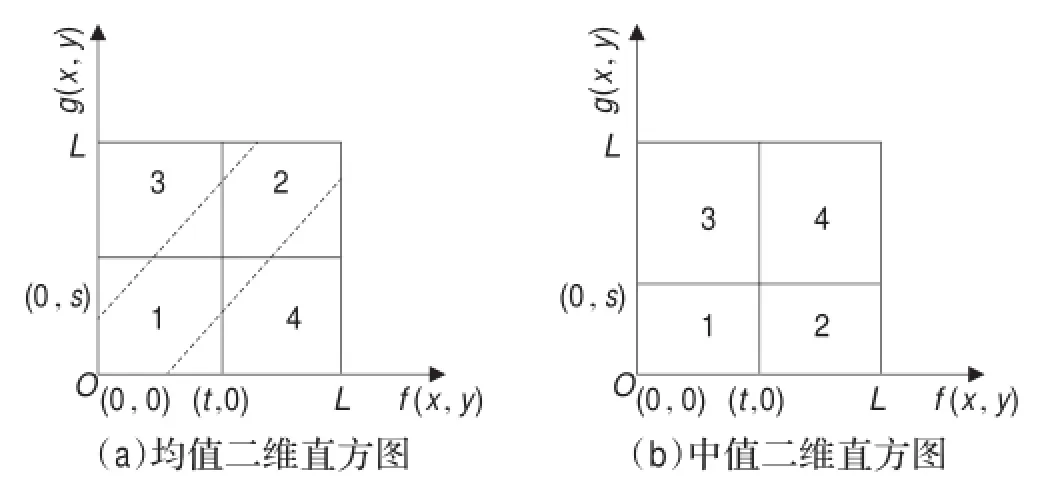
圖1 二維直方圖的構建方式

從圖1（b）可看出，對于中值二維直方圖，由于圖像中目標和背景內像素點的鄰域灰度絕對差較小，所占比例很大，因此，概率分布高峰主要集中在區域1和區域2。而位于區域3和區域4的邊緣點和噪聲點的灰度絕對差較大，在圖像中所占比例較小。

3.2 閾值選擇

利用新的二維直立圖和對稱卡方散度設計改進的二維最小卡方散度閾值選擇方法。

令原始圖像F離散概率分布為：

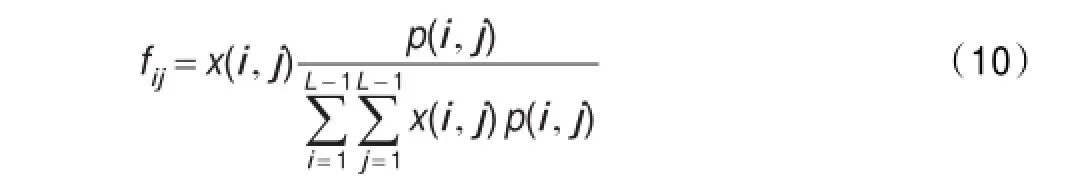
分割后圖像G的離散概率分布為：

為了提高抗噪性效果，本文采用了關鍵閾值分割，即在進行分割時閾值向量中起決定作用的那個分量，依據式（20），就是閾值向量的差。然后用此閾值對鄰域圖像，即濾波后的圖像進行分割：

4 仿真實驗與分析

實驗選取文獻[5]中的Otsu法和文獻[10]中Li和Lee提出的最小交叉熵法結合傳統均值二維直方圖，構成二維的Otsu和二維最小交叉熵方法，并用這兩種方法與本文的方法進行對比實驗。實驗用計算機是Pentium?CPU2.66 GHz，2 GB內存，編程工具是Matlab7.0。

形象生動的比喻手法能將事物寫得更具體，給人留下深刻的印象。如《臺灣的蝴蝶谷》中“有的山谷里有幾種蝴蝶，上下翻飛，五彩繽紛，就像誰在空中撒了一把把五顏六色的花瓣，隨風飄來，又隨風飄去。”“一把把五顏六色的花瓣”指的是山谷里“上下翻飛，五彩繽紛”的幾種蝴蝶，寫出了蝴蝶飄飄悠悠的柔美姿態，加上多種多樣的絢麗色彩，這美麗的畫面就像電影一樣呈現在學生的眼前。

4.1 性能評估

對于圖像分割方法性能的評估，目前沒有一種絕對有效的客觀標準。為了對各方法分割性能作定量分析，本文選用文獻[10]中使用的誤分類誤差（Misclassification Error，ME）作為客觀評價標準。定義如下：

其中，Bo、Fo分別表示圖像的真實背景及前景，BT、FT分別表示分割圖像的背景及前景，|·|表示集合·的勢。

為了測試各方法性能，首先在一幅合成圖像上對各方法進行對比。圖2（a）列出的是該合成圖像的原始圖像，該圖像前景由漢字“國”字構成，其像素灰度級為60，背景灰度級為200，圖像大小為170×170。圖2（b）為原始圖像的真實分割圖。圖2（c）～（e）列出了原始圖像分別疊加了密度為0.1的椒鹽噪聲和均值為0，方差為0.01的高斯噪聲以及同時含有以上兩種噪聲的噪聲圖像。圖2（f）～（h）為幾種二維分割方法對圖2（c）處理的結果。圖2（i）～（k）是對圖2（d）處理的結果，圖2（l）～（n）是對圖2（e）處理的結果。

圖2 合成噪聲圖像的二維直方圖法閾值結果

從圖2的實驗結果可以看出，用本文方法得到的結果清晰地把目標“國”字分離出來了，且殘留的噪聲點也較少。可見本文方法分割結果是幾種二維方法中最好的。

表1列出的是圖2中不同分割方法對幾種噪聲圖像進行分割時獲得的最佳閾值、誤分類誤差及運行時間。

表1 噪聲圖像二維分割結果

由式（24）可知，ME值越小，算法的分割性能應該越好。從圖2和表1的結果可看出，不管對于單一噪聲還是混合噪聲，本文的方法都可以獲得比其他方法明顯更小的分割誤差。又由于卡方散度本身計算過程相對簡單，因此本文方法也是以上各組實驗中用時最少的一種。

圖3 混合噪聲圖像分割的ME與時間

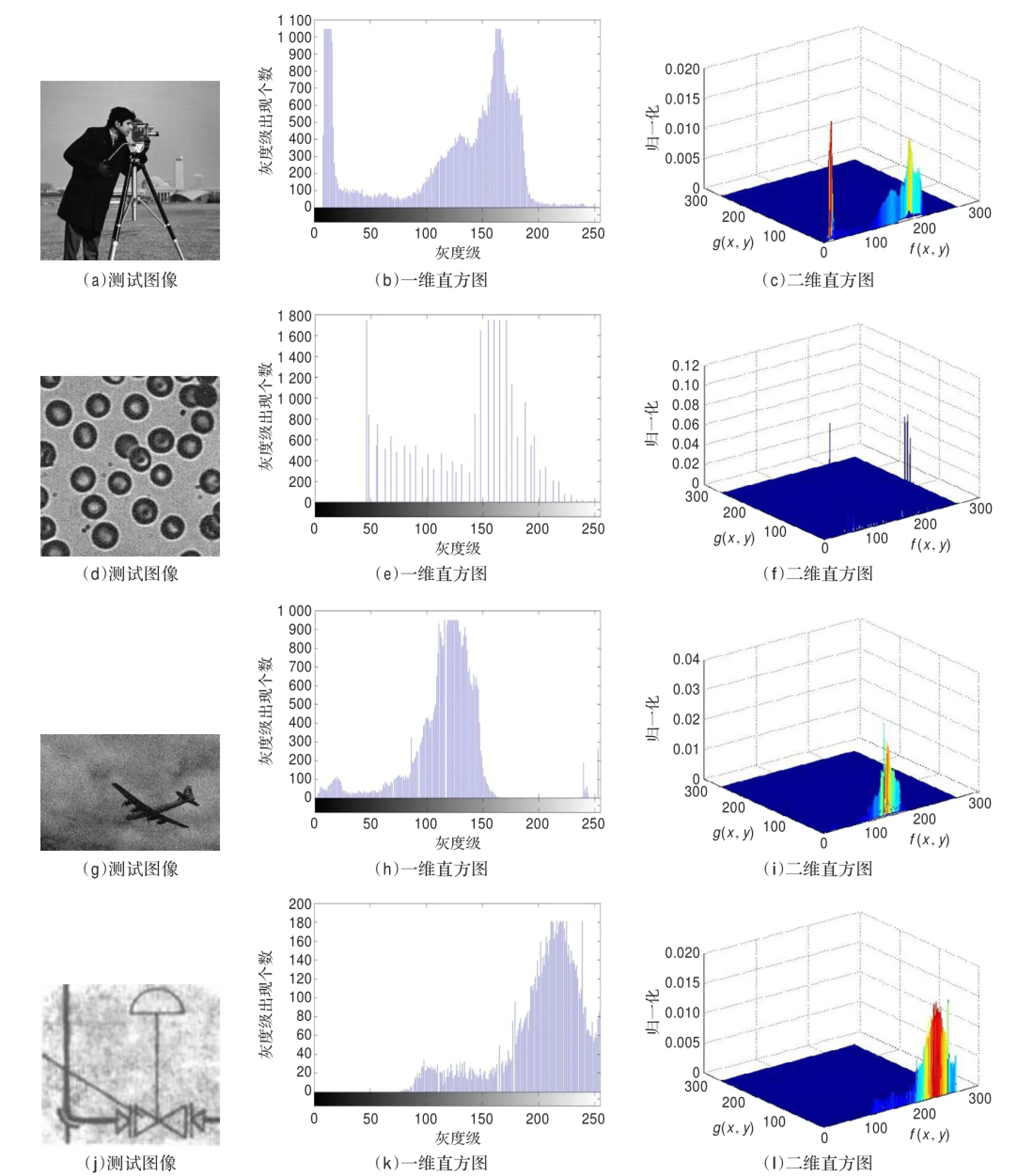
圖4 測試圖像與其直方圖

由圖3可知，在處理混合噪聲圖像時，本文的方法不管在誤分類誤差還是運行時間上都明顯優于二維Otsu法和交叉熵法。

4.2 真實圖像上的實驗

為了驗證本文方法在真實圖像上的有效性，在大量對比實驗的基礎上，本文選取四幅具有不同直方圖特點的圖像。圖4列出了這些原始測試圖像及其相應的一維直方圖和二維直方圖。不同二維方法的圖像分割結果如圖5所示。

表2和表3列出了幾種方法對這四幅不同類型測試圖像進行分割時的運行時間和獲得的分類誤差。

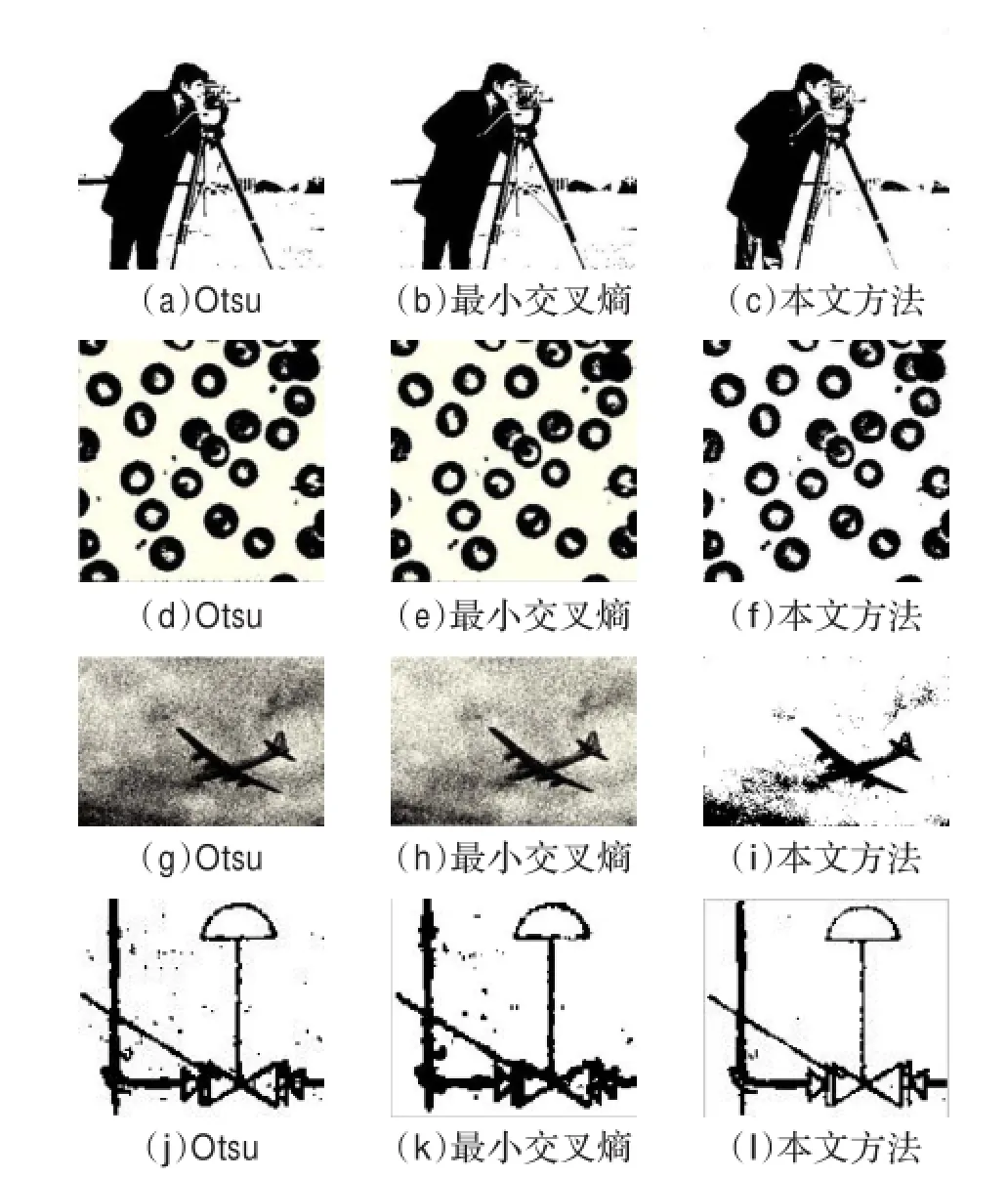
圖5 不同二維方法的圖像分割結果

表2 測試圖像分割算法的處理時間s

表3 測試圖像分割結果的誤分類誤差（ME）

由以上結果來看，對不同直方圖特點的測試圖像，基于改進卡方散度在運行時間和分割誤差方面都比Otsu和交叉熵閾值法都有所改善。

5 結束語

本文提出了一種改進的卡方散度圖像閾值化分割方法。在該方法中，通過對稱卡方散度公式并利用新的二維直方圖設計了一種適合圖像閾值化問題的準則函數，最后用關鍵閾值對濾波圖像進行閾值分割。與現有的閾值化方法相比，在合成圖像的仿真實驗中，得到的誤分類誤差指標說明了提出方法的優越性，本文方法能夠得到更好的分割結果。在真實圖像上的實驗也表明方法對紛繁復雜的圖像進行閾值化時具有更好的適應性。值得提出的是，本文方法還大大提高了算法的處理所需時間。然而作為交叉熵的外延處理方法，并沒有研究它在處理圖像系統時的非廣延性。因此，對算法的進一步優化也是下一步需要做的工作。

[1]Gonzalez R C，Woods R E.數字圖像處理[M].阮秋琦，阮宇智，譯.2版.北京：電子工業出版社，2003.

[2]Weszka J S.A survey of threshold selection techniques[J]. Computer Graphics and Image Processing，1978，7（2）：259-265.

[3]Sahoo P K，Soltani S，Wong A K C，et al.A survey of thresholding techniques[J].Computer Vision，Graphics，and Image Processing，1988，41（2）：233-260.

[4]Sezgin M，Sanakur B.Survey over image thresholding techniques and quantitative performance evaluation[J].Journal of Electronic Imaging，2004，13（1）：146-165.

[5]Otsu N.A threshold seclection method from gray-level histograms[J].IEEE Transactions on Systems，Man and Cybernetics，1979，9（1）：62-66.

[6]Kittler J，Illingworth J.Minimum error thresholding[J].Pattern Recognition，1986，19（1）：41-47.

[7]Pun T.A new method for grey-level picture thresholding using the entropy of the histogram[J].Signal Processing，1980，2（3）：223-237.

[8]Kapur J N，Sahoo P K，Wong A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision，Graphics and Image Processing，1985，29（3）：273-285.

[9]Wong A K C，Sahoo P K.A gray-level threshold selection method based on maximum entropy principle[J].IEEE Transactions on Systems，Man，and Cybernetics，1989，19（4）：866-871.

[10]Li C H，Lee C K.Minimum cross entropy thresholding[J]. Pattern Recognition，1993，26（4）：617-625.

[11]Li C H，Tam P K S.An iterative algorithm for minimum cross entropy thresholding[J].Pattern Recognition Letters，1998，19（8）：771-776.

[12]Brink A D，Pendock N E.Minimum cross-entropy threshold selection[J].Pattern Recognition，1996，29（1）：179-188.

[13]Pearson K.On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling[J].Phil Mag，1900，50：157-172.

[14]喬韡韡，吳成茂.基于卡方散度閾值方法的圖像分割研究與實現[J].計算機應用與軟件，2008，25（10）：78-81.

[15]唐英干，邸秋艷，趙立興，等.基于二維最小Tsallis交叉熵的圖像閾值分割方法[J].物理學報，2009，58（1）：10-14.

[16]張恒，雷志輝，丁曉華.一種改進的中值濾波算法[J].中國圖象圖形學報，2004，9（4）：409-411.

WANG Chen1，2,FAN Yangyu1,XIONG Lei2

1.School of Electronics&Information,Northwestern Polytechnical University,Xi’an 710072,China
2.School of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China

Traditional cross-entropy thresholding method is sensitive to noise and with much longer computation time.In order to improve the performance of this algorithm,a novel image thresholding segmentation criteria based on 2-D minimum chi-square divergence is proposed.A novel 2-D histogram based on improved median filter is structured.The difference between the segmented image and the original one is measured by the symmetric chi-square divergence.The neighborhood image is segmented with the key threshold to obtain better segmentation effects.Experimental results demonstrate that the proposed method’s computing time is much less,and its segmentation effect and anti-noise are better than 2-D minimum cross entropy and 2-D Otsu.

image segmentation;thresholding method;cross entropy;chi-square divergence;key threshold

傳統的交叉熵閾值法具有抗噪性能差，計算時間長等問題。為了改進算法的性能，提出了一種二維最小卡方散度圖像閾值化分割新準則，構建了基于改進中值濾波的新型二維直方圖。利用對稱卡方散度描述分割前后圖像之間的差異程度。使用關鍵閾值對濾波圖像進行分割，達到最佳的分割效果。實驗結果表明，與二維Otsu和二維最小交叉熵法相比，提出的方法不僅大大縮短了分割時間，而且分割性能與抗噪性能更強。

圖像分割；閾值法；交叉熵；卡方散度；關鍵閾值

A

TP391

10.3778/j.issn.1002-8331.1310-0221

WANG Chen,FAN Yangyu,XIONG Lei.Improved image segmentation based on 2-D minimum chi-square-divergence.Computer Engineering and Applications,2014,50（18）：8-13.

國家自然科學基金（No.61379104）。

王晨（1977—），女，博士研究生，講師，主要研究領域：圖像分割、特征檢測；樊養余（1960—），男，博士（后），教授，博導，主要研究領域：數字圖像處理、信號處理、虛擬現實技術；熊磊（1976—），男，博士，副教授，主要研究領域：數字圖像處理、模式識別。E-mail：wwangchen77@163.com

2013-10-21

2014-03-10

1002-8331（2014）18-0008-06

CNKI網絡優先出版：2014-04-01，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0221.html