基于優勢關系全序化的球隊攻守能力評價研究

林偉華，李進金

漳州師范學院數學與信息科學系，福建漳州 363000

基于優勢關系全序化的球隊攻守能力評價研究

林偉華，李進金

漳州師范學院數學與信息科學系，福建漳州 363000

1 引言

足球比賽是一項勝負難料的體育運動，比賽中“以弱勝強”、“爆冷門”的現象時有發生，使得球王貝利被喻為“烏鴉嘴”，業內人士無奈地解釋為“足球是圓的”。因而球隊的競技能力與比賽成績呈現出一種不對等性。這種不對等性帶給足球比賽撲朔迷離的懸念和猜想，注入足球運動強大的生命力和觀賞魅力，造就了“足球世界第一運動”的譽稱。以往，對一支球隊攻守能力的強弱優差評價，通常憑借個人的主觀感覺來判斷。如何客觀評價一支球隊的攻守能力，這是當今足球界亟待解決的一個問題。

解決足球隊攻守能力評價的難題，涉及的不確定因素較多，簡單的數學工具顯得無能為力。粗糙集理論[1]作為一種刻畫不完備和不確定信息系統的數學工具，最早是由波蘭科學家Z.Pawlak于1982年提出。它無需借助先驗知識，能通過對數據的有效分析和推理，發現當中的隱含信息，揭示其潛在規律。經過國內外學者二十余年的研究，粗糙集已取得了一定的發展。目前，它已被廣泛應用于機器學習、神經網絡、模式識別、數據挖掘和設備故障等[2-6]領域。本文利用優勢關系粗糙集方法，參照足球比賽技術統計的詳實數據，對參賽球隊的攻守能力進行量化分析，綜合評價。分別從進攻能力、防守能力、攻守綜合能力三個方面對參賽球隊進行優勢評價，從而得到球隊攻守能力的合理排序關系。

2 預備知識

為了便于理解，首先介紹粗糙集理論的有關基本概念。

定義1.1[7]U上的關系R稱為等價關系，若滿足以下性質：

則[xi]≤B表示在屬性集B條件下，優于對象xi的所有對象集合，稱為xi的優勢類。

經典粗糙集模型是建立在等價關系上的，而優勢粗糙集模型是處理屬性偏好有序的問題。偏序關系全序化的粗糙集方法是在偏序關系上建立優勢關系，把連續值信息系統轉化為優勢關系模型，再通過關系模型得到對象間的排序。

3 基于粗糙集方法的球隊進攻、防守、攻守能力的綜合評價

3.1 評價指標確定和比賽數據的獲取

通過查閱相關文獻資料，從中收集反映比賽攻守能力的統計指標，初步建立本文研究的統計指標草案。在通過當面訪談和電子郵件方式對統計指標的合理性進行專家問卷調查，最終確立統計指標。具體情況如下：球隊進攻能力的評價屬性A確定為進球a1、射門a2、傳威脅球a3、傳球a4、角球a5、控球率a6；球隊防守能力的評價屬性B確定為失球b1、被射門b2、搶斷b3；球隊攻守能力的評價屬性記為C。

本文主要選取了2012年歐洲杯官網16支參賽球隊的比賽場均數據，將數據四舍五入保留小數點后兩位得到如表1[8]所示。這16支球隊分別為：西班牙x1，意大利x2，德國x3，葡萄牙x4，英格蘭x5，捷克x6，希臘x7，法國x8，俄羅斯x9，克羅地亞x10，瑞典x11，丹麥x12，烏克蘭x13，波蘭x14，荷蘭x15，愛爾蘭x16。

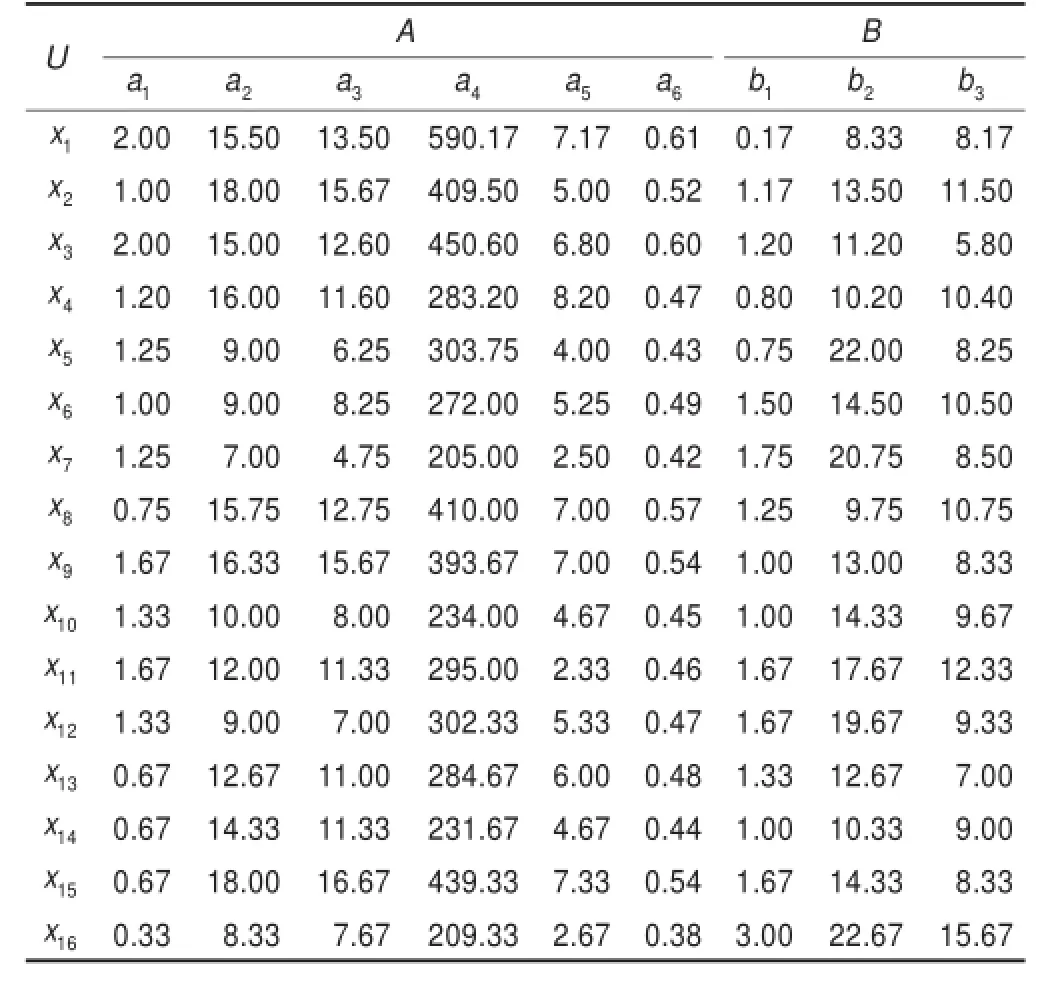
表1 2012年歐洲足球錦標賽場均數據表次

3.2 評價步驟及計算結果

為了方便處理，在計算過程中，將表1中與防守能力呈負相關的統計指標“場均失球數”和“被射門場均數”設為負值。

步驟1由式（1）計算可得，

（1）各球隊進攻能力的優勢類分別為：

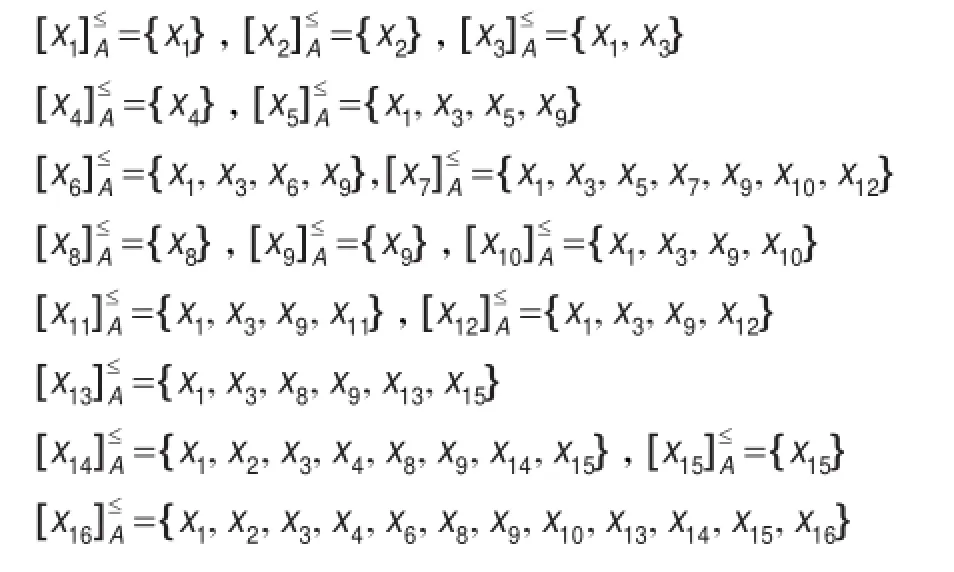
（2）各球隊防守能力的優勢類分別為：

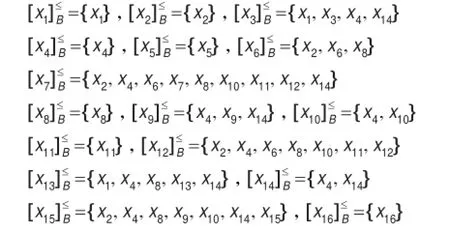
步驟2由式（2）可得到球隊之間的進攻和防守優勢矩陣如表2和表3所示。

步驟3由式（3）可得球隊的進攻綜合優勢度RA(xi)和防守綜合優勢度RB(xi)分別為：

（1）球隊的進攻綜合優勢度RA(xi)為：

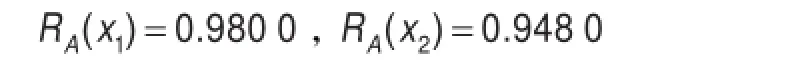
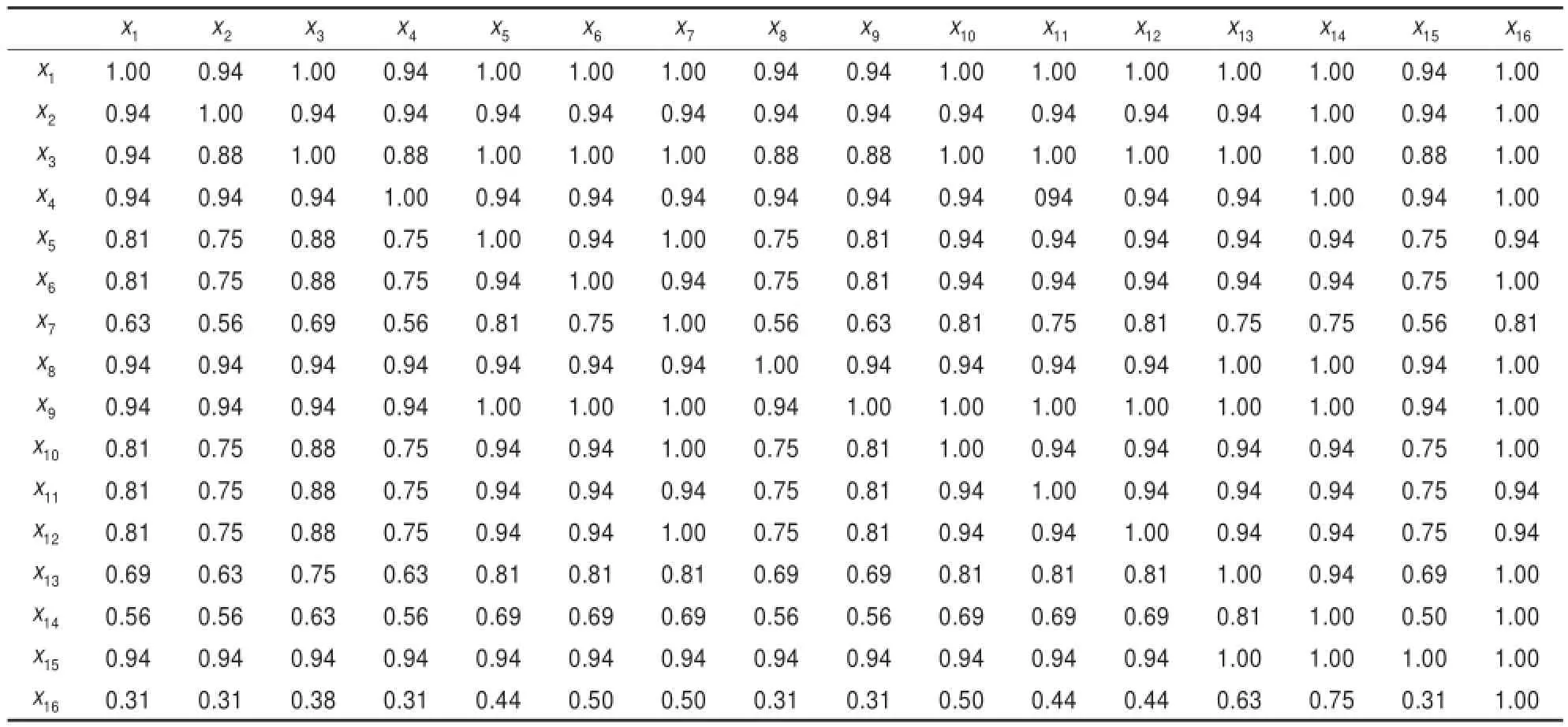
表2 球隊之間的進攻優勢矩陣

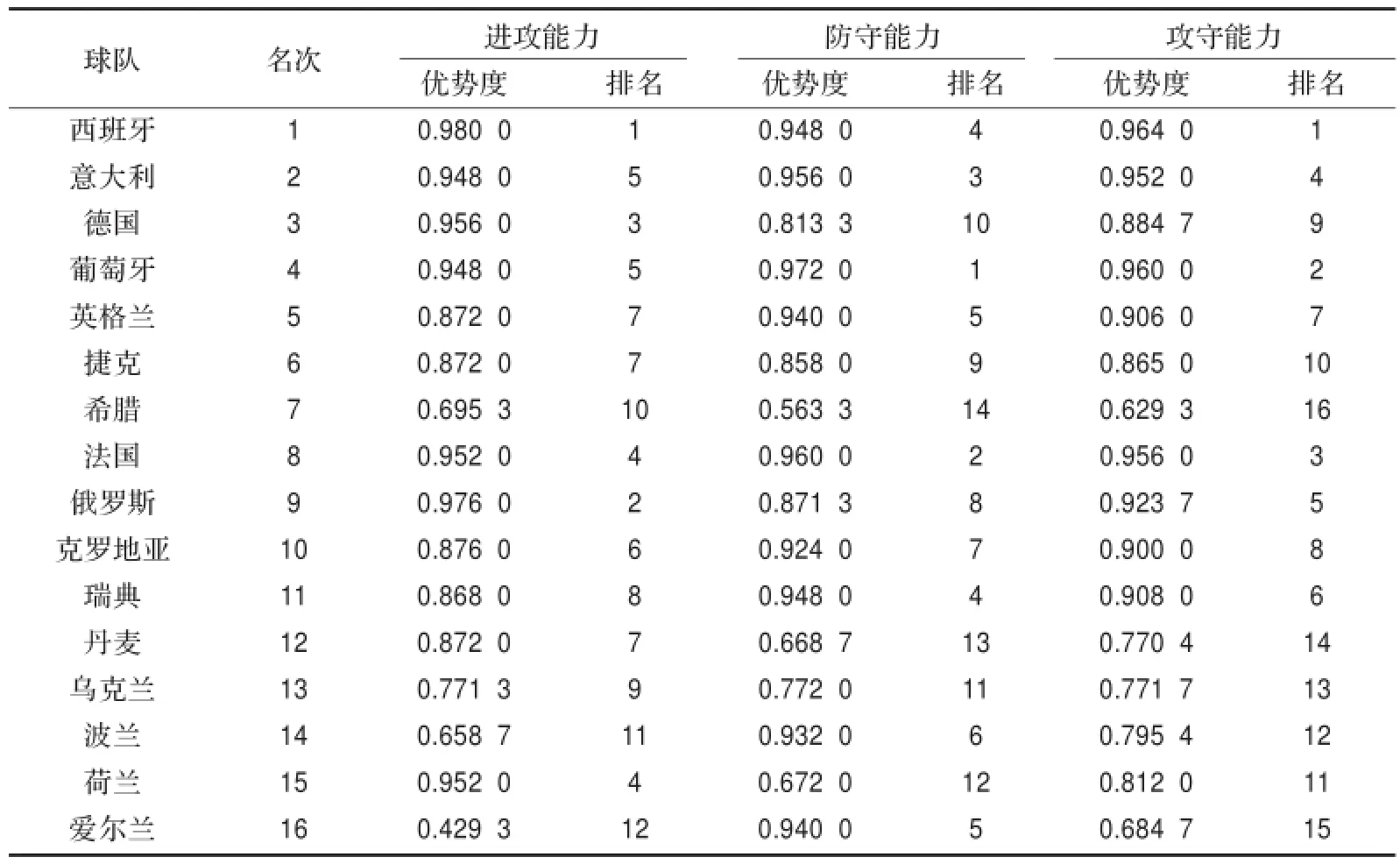
表4 2012年歐洲杯足球賽球隊三個能力優勢度對比一覽表

查t值表，n′=16-2=14，t(14)0.05=2.145。算得t= 3.283 8＞t(14)0.05=2.145，P＜0.05。說明各球隊比賽成績名次與攻守能力排名之間具有顯著性意義。優勢度排名較客觀真實地反映了比賽成績，證明選用的進球、射門等九個指標能夠有效地反映出球隊攻守技戰術能力。因此，優勢關系粗糙集方法在足球比賽中具有實際應用意義。

優勢度評價結果分析：

攻強守弱的典型代表球隊（如俄羅斯和荷蘭隊）最終獲取第九名和第十五名成績；同時，守強攻弱的球隊（如愛爾蘭和瑞典隊）最終成績為第十六名和十一名；攻守平衡的球隊（如西班牙、意大利和葡萄牙隊）均獲取了進入四強的佳績。從優勢度排序分析得知，足球比賽中球隊不僅要具備強大的進攻能力，也應具備堅固的防守能力，只有達到攻守兼備和攻守平衡，才能取得好的成績。

4 結論

本文通過基于優勢關系的粗糙集方法，實現了對2012年歐洲足球錦標賽決賽的16支球隊的進攻能力、防守能力和攻守綜合能力的評價。而后又采用等級相關分析法檢驗顯示，優勢度評價結果較客觀真實地反映了比賽成績。優勢關系粗糙集方法在足球比賽中具有實際運用意義，為足球比賽的技戰術研究探索出了一種合理有效的數學研究方法。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science，1982，11：341-356.

[2]楊常清.基于粗糙集的屬性約簡算法[J].西北大學學報：自然科學版，2012，42（2）：223-225.

[3]楊冬風，楊冬秀.粗糙神經智能疑似乳癌圖像分類方法研究[J].計算機工程與應用，2010，46（12）：188-191.

[4]高建來，運士偉，張永勝.融合粗糙集與球形支持向量機的多分類識別[J].河南科技大學學報：自然科學版，2011，32（5）：77-80.

[5]葉明全，伍長榮，胡學鋼.基于粗糙集的醫療數據挖掘研究與應用[J].計算機工程與應用，2010，46（21）：232-234.

[6]涂繼亮，潘洪亮，董德存，等.融合粗糙集和證據理論的車地無線通信設備故障診斷[J].同濟大學學報：自然科學版，2011，39（6）：870-873.

[7]張文修，仇國芳.基于粗糙集的不確定決策[M].北京：清華大學出版社，2005：113-116.

[8]2012年歐洲足球錦標賽場均數據表[EB/OL].（2012-06-18）[2012-07-01].http：//goal.euro2012.163.com/stat/teamrank/avg/ goals.html.

[9]戎家增，戎淼鋒，林瓏.現場體育統計方法[M].北京：人民體育出版社，1998.

LIN Weihua,LI Jinjin

Department of Mathematic and Information Science,Zhangzhou Normal University,Zhangzhou,Fujian 363000,China

By consulting documentations and questionnaires survey from exports,this paper sets up nine indexes of reflecting offensive and defensive ability about football teams,and collects these indexes’quantitative data from thirty-one matches between sixteen teams in the 2012 European Football Championships.Then it uses the theory of dominance relation rough set approach and grade correlation analysis to process and test it.The conclusion shows:it is more reliable to make quantitative evaluation of the indexes by adopting the theory of dominance relation rough set approach,which reflects objectively offensive and defensive ability of football teams.It reveals the tendency of football development,and explores a kind of suitable and available method for the ability of football teams in the meantime.

dominance relation;rough set approach;grade correlation analysis;offensive ability;defensive ability;offensive and defensive ability

通過查閱文獻和專家問卷調查，選取了反映球隊技戰術能力的九項主要指標，對2012年歐洲杯足球賽決賽階段的16支球隊31場比賽進行統計，并運用優勢關系粗糙集方法和等級相關分析法對所得數據進行處理和檢驗。結果表明：運用優勢關系粗糙集方法對球隊的技戰術指標進行綜合評價具有較高的可靠性，能夠客觀地反映各隊技戰術能力。在揭示足球技戰術發展趨勢的同時，探索出合理有效的量化評價球隊技戰術能力的方法。

優勢關系；粗糙集方法；等級相關分析法；進攻能力；防守能力；攻守能力

A

TP18

10.3778/j.issn.1002-8331.1210-0062

LIN Weihua,LI Jinjin.Team offensive and defensive ability evaluation research based on dominance relation linearization method.Computer Engineering and Applications,2014,50（18）：246-250.

國家自然科學基金（No.10971185，No.10971186，No.71140004）；福建省資助省屬高校科研專項（No.JK2011031）。

林偉華（1982—），女，在讀碩士研究生，研究方向：粗糙集理論及其應用；李進金（1960—），男，教授，研究方向：拓撲學、粗糙集理論及其應用。E-mail：740816193@qq.com

2012-10-09

2012-12-17

1002-8331（2014）18-0246-05

CNKI網絡優先出版：2013-01-11，http://www.cnki.net/kcms/detail/11.2127.TP.20130111.0951.006.html