模的Gorenstein cotorsion包絡

張豫岡

(蘭州工業學院基礎學科部,甘肅 蘭州 730050)

模的Gorenstein cotorsion包絡

張豫岡

(蘭州工業學院基礎學科部,甘肅 蘭州 730050)

通過與模的內射包絡相比較,討論了模的基本擴張與Gorenstein cotorsion包絡及單模的Gorenstein cotorsion包絡,給出了模的Gorenstein cotorsion包絡具有類似性質的一些充分條件.

Gorenstein cotorsion模;(預)包絡;基本擴張

1 引言

Gorenstein同調代數受到了國內外許多學者的廣泛關注[13].作為平坦模的推廣, Enochs等引入了 Gorenstein平坦模的概念.稱模 M 是 Gorenstein平坦的[4],如果存在平坦模的正合序列

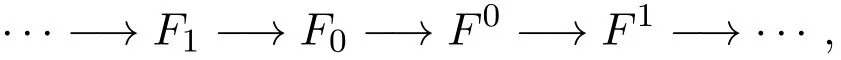
假設X,Y是R-模類.稱(X,Y)是余撓理論,如果X=⊥Y且Y=X⊥.其中,

⊥Y={M|Ext(M,Y)=0,?Y∈Y},X⊥={N|Ext(X,N)=0,?X∈X},

分別稱為Y的左正交類和X的右正交類.

假設X是R-模類且關于同構、直和因子及有限直和封閉,M 是R-模,X∈X.稱同態f:M →X是M 的X-預包絡,如果對任意同態g:M →Y,其中Y∈X,存在同態h:X→Y,使得h?f=g.這也等價于對于任意Y∈X,是正合序列.進而,若有同態 h:X → X,使得當 h?f=f時 h是 X 的自同構,則稱f:M→X是模M的X-包絡.

若R是使得所有Gorenstein平坦模的類GF關于擴張封閉的環,則稱其為GF-封閉環[5].由文獻[6]可知:若R是GF-封閉環,則(GF,GC)是余撓理論,并且任意模都有Gorenstein平坦覆蓋和Gorenstein cotorsion包絡.

顯然,所有內射模是Gorenstein cotorsion模.自然考慮:模的Gorenstein cotorsion包絡是否具有與模的內射包絡類似的性質？討論了模的基本擴張與Gorenstein cotorsion包絡及單模的Gorenstein cotorsion包絡,給出了模的Gorenstein cotorsion包絡具有與其內射包絡類似性質的一些充分條件.

2 模的基本擴張與Gorenstein cotorsion包絡

貫穿全文,R是GF-封閉環,模都是左R-模.記σM:M→G(M)為模M的Gorenstein cotorsion包絡.N≤M表示N是M的子模,N≤eM表示在同構意義下N是M的基本子模(或稱M是N的基本擴張),N=M表示M,N在同構意義下是相等的.

根據文獻[7]的定理3.29,可知內射模沒有真的基本擴張.對于 Gorenstein cotorsion模,有下述結論.

命題 2.1設N是Gorenstein cotorsion模,N≤eM.若M/N∈GF,則M=N.

證明考慮正合序列0→N→M→M/N→0.由于

該正合序列是可裂的,故M=N⊕M/N.同時,N≤eM.從而M/N=0,即M=N.

由文獻[8]命題8.12知:若 N≤eM,則 E(N)=E(M),其中E(N),E(M)分別表示N,M的內射包絡.

定理 2.1設N≤eM≤eG(M).以下等價:

(1)M/N∈GF;

(2)G(M)/N∈GF;

(3)G(M)=G(N).

證明(1)?(3) 令i:N→M 為包含同態.由M/N∈GF可知σN:N→G(N)可以通過i分解,即存在態射j:M →G(N)使得σN=ji.由于i是基本的,故j是單同態.同時,j可以通過Gorenstein cotorsion包絡σM:N→G(M)分解,即存在h:G(M)→G(N)使得j=hσM.同理,由σM是基本的可知h是單同態.對于

有態射g:G(N)→G(M)滿足gσN=σMi.故從而hg:G(N)→G(N)是自同構,h是滿的.進而,h:G(M)→G(N)是同構.

(3)?(2)由Wakamatsu引理可知G(N)/N∈GF,故結論成立.

(2)?(1)存在正合序列0→M/N→G(M)/N→G(M)/M→0,其中G(M)/M∈GF, G(M)/N∈GF.從而M/N∈GF.

若N≤M≤E(N),則E(M)=E(N).對于模的Gorenstein cotorsion包絡,有:

命題 2.2設N≤M≤G(N).若M≤eG(M),則G(M)=G(N).

證明令i:N→M,j:M →G(N)表示包含同態.j可以通過Gorenstein cotorsion包絡σM:M→G(M)分解,即存在f:G(M)→G(N)使得j=fσM.由σM是基本的可知f是單同態.同理,對于σMi:N→G(M),存在g:G(N)→G(M)使得σMi=gσN.從而由

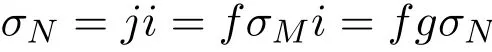
可知fg是同構.進而f是滿的,結論成立.

對于模M,稱f:M → G是特殊的Gorenstein cotorsion預包絡,如果 G∈GC,f是單的且滿足Coker(f)∈GF.由Wakamatsu引理可知任意Gorenstein cotorsion包絡是特殊的Gorenstein cotorsion預包絡.

定理 2.2假設 GF關于單同態的余核封閉.若 i:N → M 是基本單同態,且滿足Coker(i)∈GF,則M 有特殊的Gorenstein cotorsion預包絡j:M→G(N).

證明由于L=Coker(i)∈GF,故有正合序列

對于σN,有j:M→G(N),使得σN=ji,且易知j是單同態.

考慮j:M→G(N)和自然投射p:M→L的推出圖:

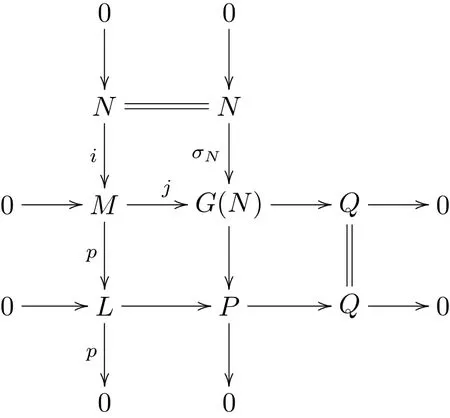
由于GF關于單同態的余核封閉,且在正合序列0→L→P→Q→0中L,P∈GF,從而Q∈GF.故結論成立.

3 單模的Gorenstein cotorsion包絡

眾所周知,單模的內射包絡是不可分解的.在一定條件下,證明了單模的 Gorenstein cotorsion包絡也具有類似的性質.

首先,需要證明如下結論.

引理 3.1設σM:M→G(M)是M 的Gorenstein cotorsion包絡.則

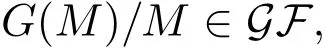
且不存在非零子模N≤G(M),使得

證明由Wakamatsu引理易知G(M)/M∈GF.

從而M=(M+N)/N.考慮正合序列

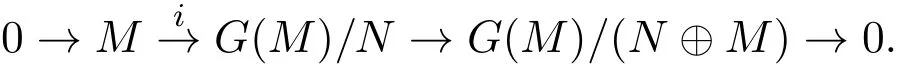
對于σM,存在

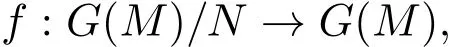
使得σM=fi.注意到i=πσM,其中π:G(M)→G(M)/N為標準投射.從而σM=fπσM, fπ是自同構,進而π是單的.即

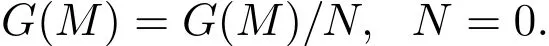
R是SF環,是指任意單R-模是平坦的.稱R是SGF環,如果任意單R-模是Gorenstein平坦的.顯然,任意SF環是SGF環.特別地,任意von Neumann正則環是SGF環.

定理 3.1假設R是SGF環,且使得Gorenstein平坦R-模的類GF關于單同態的余核封閉.則任意單模的Gorenstein cotorsion包絡是不可分解的.

證明反設存在單R-模M,滿足G(M)=M1⊕M2,Mi0,i=1,2.由于M是單的,故

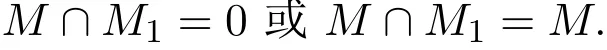
假設M∩M1=0.考慮正合序列

其中G(M)/M∈GF,且由R是SGF環得M∈GF.從而G(M)∈GF.進而M1∈GF.

在正合序列

中,M1,G(M)/M∈GF,從而由條件GF關于單同態的余核封閉,可得

根據引理3.1,M1=0,與M10矛盾.從而

同理,可證M?M2.故M?M1∩M2=0.矛盾.

[1]Enochs E E,Jenda O M G.Relative Homological Algebra[M].Berlin:Springer-Verlag,2000.

[2]Holm H.Gorenstein homological dimensions[J].J.Pure Appl.Algebra,2004,189:167-193.

[3]Mao L X,Ding N Q.Gorenstein FP-injective and Gorenstein f l at modules[J].Journal of Algebra and Its Applications,2008,7(4):491-506.

[4]Enochs E E,Jenda O M G,Torrecillas B.Gorenstein f l at modules[J].南京大學學報:數學半年刊,1993,10:1-9.

[5]Bennis D.Rings over which the class of Gorenstein f l at modules is closed under extensions[J].Comm. Algebra,2009,37(3):181-190.

[6]Yang G,Liu Z K.Gorenstein f l at cover over GF-closed rings[J].Comm.Algebra,2012,40(5):1632-1640.

[7]Rotman J.An introduction to Homological Algebra[M].New york:Academic Press,1979.

[8]Anderson F W,Fuller K R.Rings and Categories of Modules[M].2nd ed.New York:Springer,1992.

Gorenstein cotorsion envelope of modules

Zhang Yugang
(Department of Basic Sciences,Lanzhou Institute Technology,Lanzhou 730050,China)

Comparing with injective envelope of modules,we discuss the essential extension of modules and Gorenstein cotorsion envelope as well as Gorenstein cotorsion envelope of simple modules.Some sufficient conditions under which the properties of Gorenstein cotorsion envelope analogous to those of injective envelope are given.

Gorenstein cotorsion modules,(pre)envelope,essential extension

O154.2

A

1008-5513(2014)02-0173-05

10.3969/j.issn.1008-5513.2014.02.008

2013-11-12.

國家自然科學基金(11101197).

張豫岡(1978-),碩士,講師,研究方向:環模理論.

2010 MSC:16D80