二層隨機規(guī)劃逼近最優(yōu)解集的上半收斂性

周婉娜, 霍永亮, 吳凡

(1.重慶師范大學數(shù)學學院,重慶 401331;2.重慶文理學院數(shù)學與財經(jīng)學院數(shù)學研究所,重慶 402160; 3.重慶文理學院數(shù)學黨群部,重慶 402160)

二層隨機規(guī)劃逼近最優(yōu)解集的上半收斂性

周婉娜1, 霍永亮2, 吳凡3

(1.重慶師范大學數(shù)學學院,重慶 401331;2.重慶文理學院數(shù)學與財經(jīng)學院數(shù)學研究所,重慶 402160; 3.重慶文理學院數(shù)學黨群部,重慶 402160)

下層隨機規(guī)劃以上層決策變量作為參數(shù),而上層隨機規(guī)劃是以下層隨機規(guī)劃的唯一最優(yōu)解作為響應的一類二層隨機規(guī)劃問題,首先在下層隨機規(guī)劃的原問題有唯一最優(yōu)解的假設下,討論了下層隨機規(guī)劃的任意一個逼近最優(yōu)解序列都收斂于原問題的唯一最優(yōu)解,然后將下層隨機規(guī)劃的唯一最優(yōu)解反饋到上層,得到了上層隨機規(guī)劃逼近最優(yōu)解集序列的上半收斂性.

二層隨機規(guī)劃,最優(yōu)解集,上半收斂

1 引言

近幾十年來,國內(nèi)外許多學者對隨機規(guī)劃的逼近理論有了較深入的研究,隨機規(guī)劃穩(wěn)定性理論的內(nèi)容也得到了極大的豐富.文獻[1]分別對隨機規(guī)劃的期望模型、機會約束模型以及二階段固定補償模型作了全面的探討,得到了一些好的結果.文獻[2]研究了當離散化隨機變量序列依分布收斂時,隨機規(guī)劃逼近解的收斂性.文獻[3]將隨機函數(shù)引入隨機規(guī)劃問題中,研究了最優(yōu)函數(shù)逼近問題的收斂性.文獻[4-5]討論了在Fourtet-Mourier度量上隨機規(guī)劃問題的穩(wěn)定性.文獻[6]研究了逼近隨機規(guī)劃可行集序列的收斂性條件,得到了隨機規(guī)劃逼近最優(yōu)解集的上半收斂性.文獻[7]利用Kuratowski收斂,研究了二層規(guī)劃問題的逼近法的有關上圖收斂性問題.文獻[8]研究了以下層最優(yōu)值作為響應反饋到上層的一類二層規(guī)劃的逼近問題的收斂性.目前對二層隨機規(guī)劃穩(wěn)定性的研究相對較少,作者利用上圖收斂性,分別研究了下層隨機規(guī)劃最優(yōu)解集序列的收斂性和假設原下層隨機規(guī)劃有唯一最優(yōu)解時,上層隨機規(guī)劃最優(yōu)解集序列的收斂性.本文研究的內(nèi)容與文獻[7-8]的區(qū)別在于:

(1)研究了二層隨機規(guī)劃最優(yōu)解集的上半收斂性,而文獻[7-8]只研究了一般二層規(guī)劃目標函數(shù)的上圖收斂性;

(2)研究的是以下層隨機規(guī)劃的唯一最優(yōu)解作為響應反饋到上層的一類二層隨機規(guī)劃,而文獻[7-8]研究的是以下層規(guī)劃的最優(yōu)值作為響應反饋到上層的一類二層規(guī)劃.

本文考慮如下的二層隨機規(guī)劃問題:

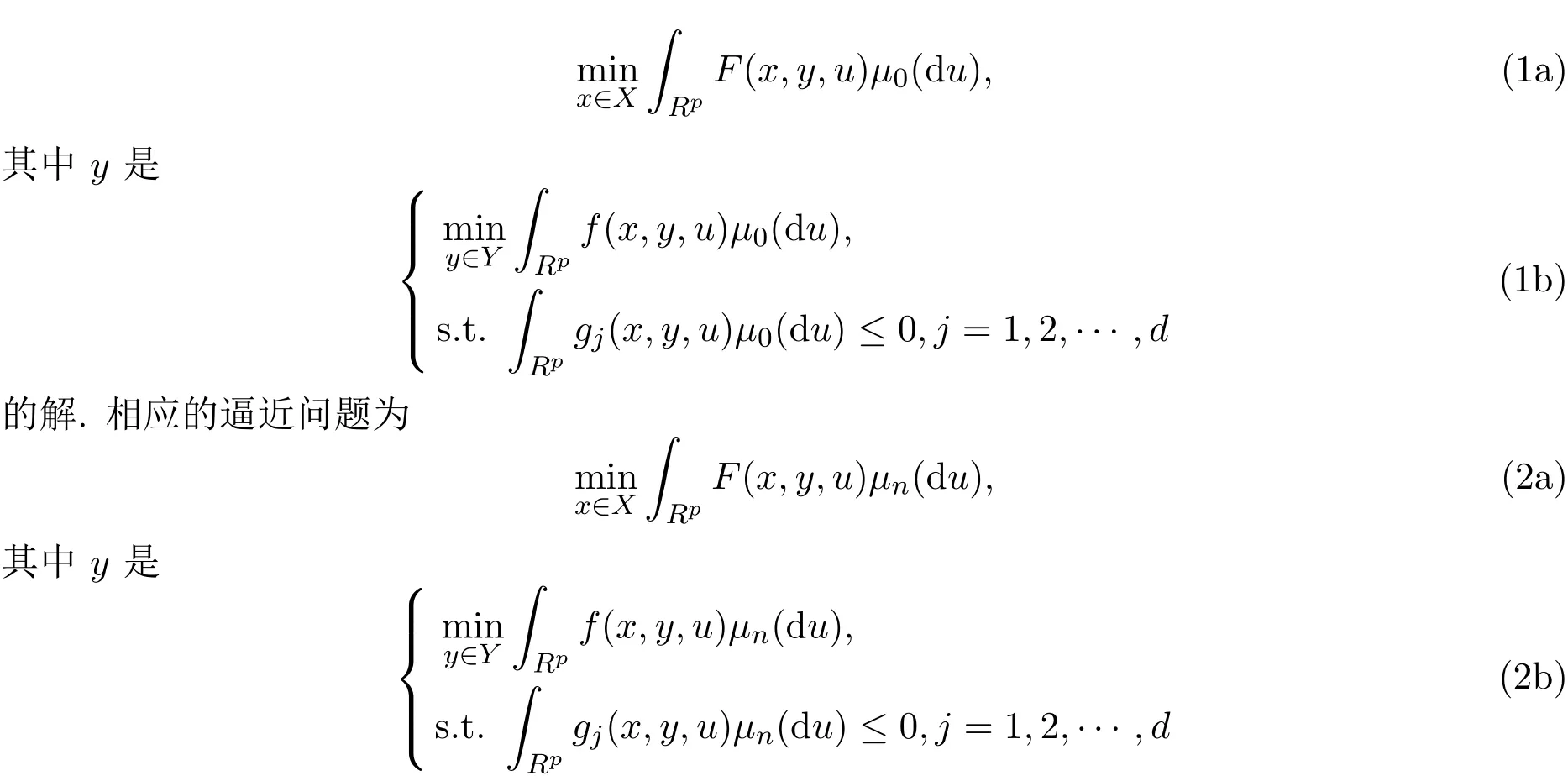
的解.其中,本文始終假設X和Y分別是Rn和Rm上的緊集,F,f,g是定義在Rn×Rm×Rp上的函數(shù),μ0=P?ξ?1,μn=,ξ為定義在概率空間(?,F,P)上的m維隨機向量,ξn為ξ的離散化逼近隨機變量序列.

2 下層隨機規(guī)劃最優(yōu)解的收斂性

為討論上層隨機規(guī)劃問題最優(yōu)解集的收斂性,首先討論下層隨機規(guī)劃問題最優(yōu)解的收斂性.當x0∈Rn固定時,下層隨機規(guī)劃問題的原問題變?yōu)?/p>

問題(3)和問題(4)的可行集分別記為S0(x0)和Sn(xn),即

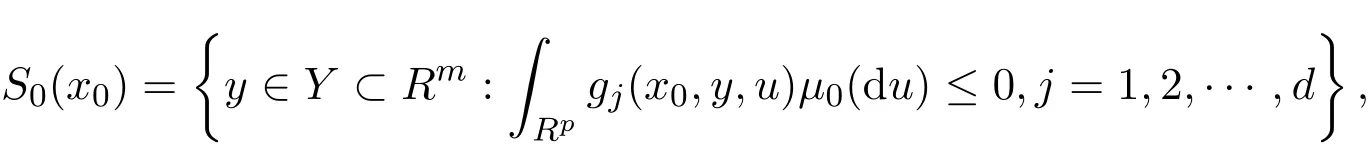
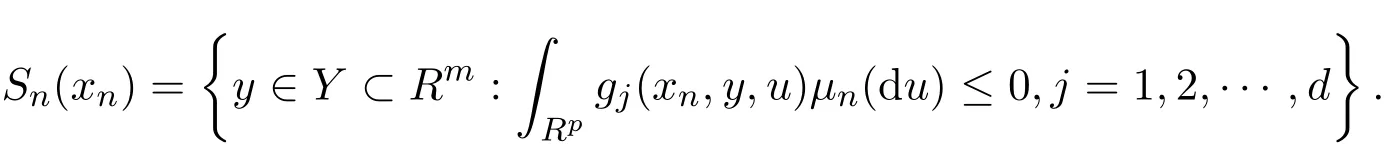
下層隨機規(guī)劃問題(3)和問題(4)又可轉化為與其等價的無約束規(guī)劃問題(5)和問題(6):

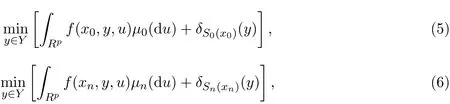
其中

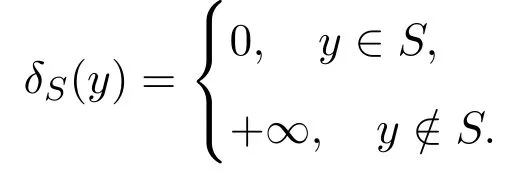
問題(5)和問題(6)的最優(yōu)解集分別記為M0(x0)和Mn(xn).

引理 2.1(1)若xn→x0且f(x,y,u)在 X×Y×Rp上連續(xù)有界,μnw→μ0,則對任意的y0∈Rm,且yn→y0,有

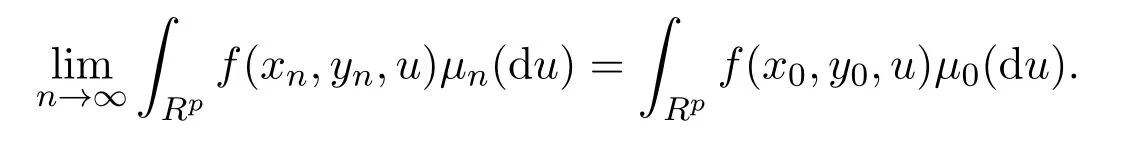
(2)若xn→x0且f(x,y,u)在 X×Y×Rp上連續(xù)有界,則對每個固定的n0,

均在Rm上連續(xù).

證明(1)設 xn→ x0,且 yn→ y0,令 gn(u)=f(xn,yn,u),g0(u)=f(x0,y0,u),由于f(x,y,u)在 X×Y×Rp上連續(xù),所以gn(u)和g0(u)在Rp上連續(xù),且gn(u)連續(xù)收斂于g0(u),由于f(x,y,u)有界,則函數(shù)族{g0;gn,n∈N}等度有界,由于μnμ0,則有

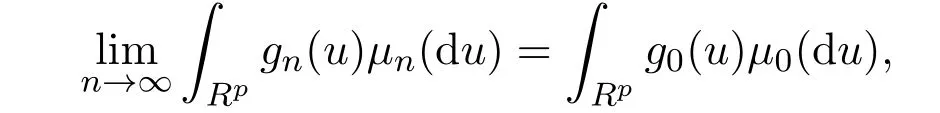
即

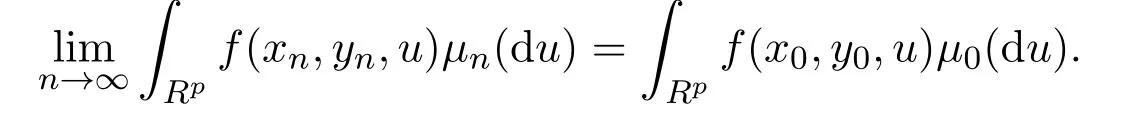
(2)在(1)中分別令

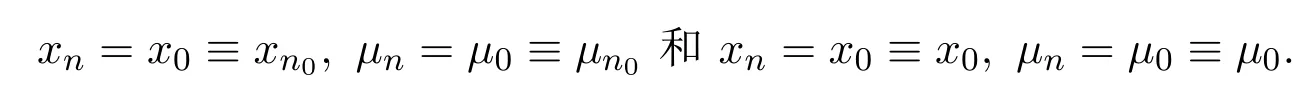
引理 2.2若xn→x0,令

那么:

(1)若gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下半連續(xù)且下有界,μn→wμ0,則(y)下半收斂于(y).

(2)若gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下半連續(xù)且下有界,對每個固定的n0,則(y)和(y)在Rm上下半連續(xù).

(3)若gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下半連續(xù)且下有界,對每個固定的y, gj(x,y,u)關于(x,u)上半連續(xù),且,則

證明設xn→x0,且yn→y0,令tn(u)=gj(xn,yn,u),t0(u)=gj(x0,y0,u),由gj(x,y,u)

在 X×Y×Rp上下半連續(xù),則對任意 u0∈Rp,且 un→ u0,有而gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下有界,則函數(shù)族{t0;tn,n∈N}等度下有界,而且則

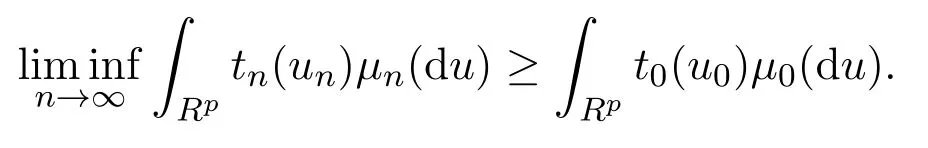
(2)類似于(1)的證明,分別令

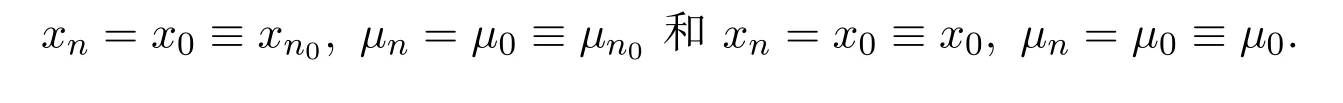
(3)在引理2.1中令f(x,y,u)=gj(x,y0,u),j=1,2,···,d.

定義 2.1[6]稱可行集 S0(x0)是正則的,即滿足 S0(x0)=clS0(x0)°,并且 S0(x0)°?,其中{∫}

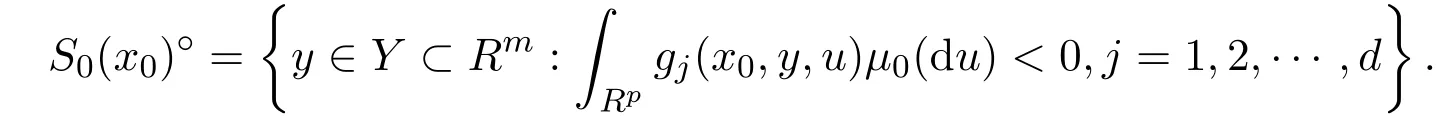
定義 2.2[7]如果xn→x0,集合序列滿足:

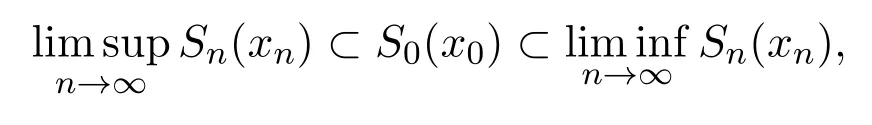
則稱集合序列{Sn(xn)}收斂于S0(x0),記為,意即

(1)如果對任意yn→y0,且yn∈Sn(xn),則y0∈S0(x0);

(2)對任意y0∈S0(x0),則存在yn→y0,那么對充分大的n,有yn∈Sn(xn).

引理 2.3若xn→x0,設gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下半連續(xù)且下有界,對每個固定的y,gj(x,y,u)關于(x,u)上半連續(xù),可行集S0(x0)正則,且則

(1)存在n0,當n≥n0時,Sn(xn)為非空緊集;(2)

證明(1)由于S0(x0)正則,則S0(x0)°/?,設y0∈S0(x0)°,即

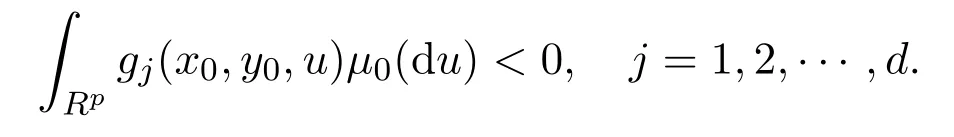
并且,y0∈Y,令

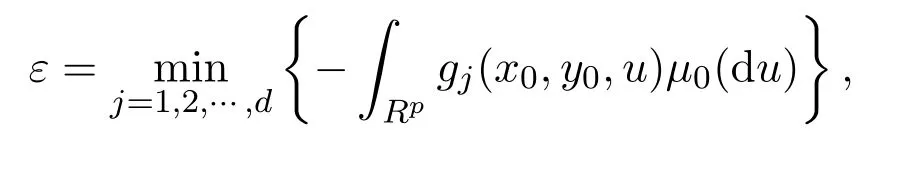
則ε>0,由引理2.2的(3)可知,對每個固定的y0,存在nj,當n≥nj,有

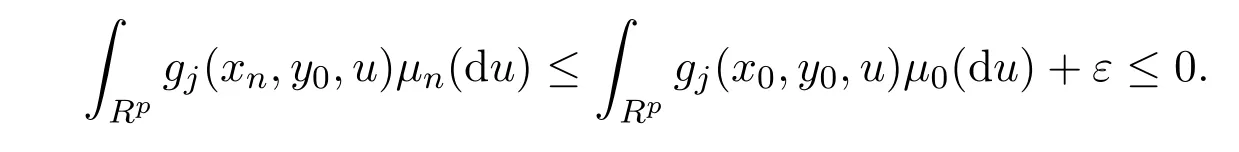
令n0=,當n≥n0,有

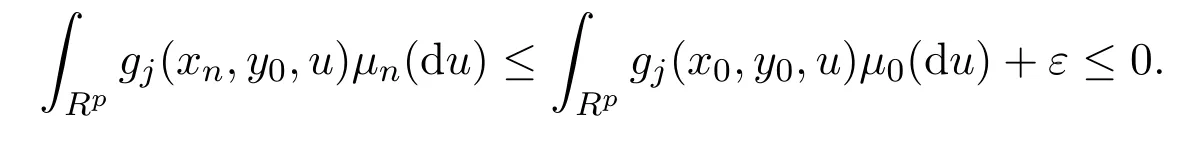
因此,當 n≥n0時,有 y0∈Sn(xn),即 Sn(xn)/?,由引理 2.2的 (2)知,Sn(xn)為閉集,而Sn(xn)?Y及Y的緊致性,所以Sn(xn)為非空緊集.

yn→y0,由引理2.2的(1)可得,對每個j,均有

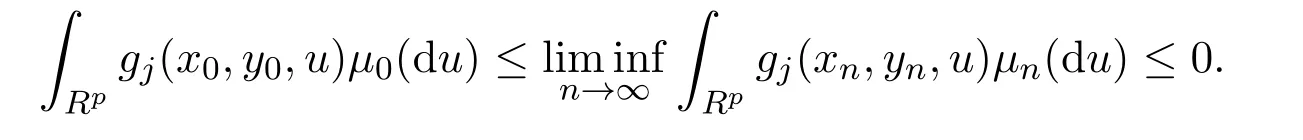
而yn∈Y及由Y的緊致性,則y0∈Y,于是

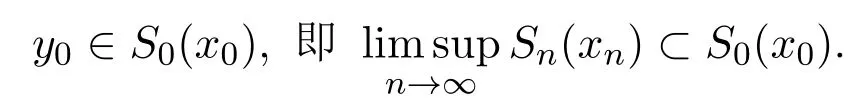
再證明S0(x0)?設y0∈S0(x0),由于S0(x0)正則,則S0(x0)=clS0(x0)°,即存在{zn}?S0(x0)°,使得zn→y0.由(1)的證明可知,對每個zn,存在Nn,當n≥Nn時有zn∈Sn(xn),構造下列序列yn,

由yn的構造可知,對所有n>N1,有yn∈Sn(xn),另一方面,由zn→y0,則有yn→y0,所以綜上,

定義 2.3如果,稱上圖收斂于記為,是指

(1)對任意yn→y0,有

(2)存在某個yn→y0,使得

引理 2.4若xn→x0,且f(x,y,u)在X×Y×Rp上連續(xù)有界,gj(x,y,u),j=1,2,···,d,在 X×Y×Rp上下半連續(xù)且有界,對每個固定的 y,gj(x,y,u)關于(x,u)上半連續(xù),可行集S0(x0)正則,且則有

證明首先,證明對任意y0∈Rm,且yn→y0,(7)式成立.

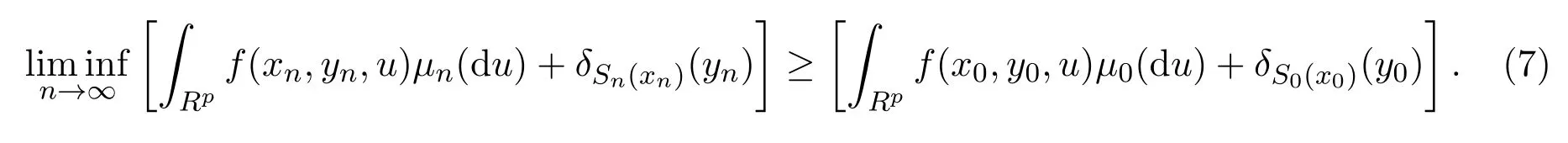
對y0∈Rm分兩種情況討論.

(i)如果y0∈S0(x0),且yn→y0,由引理2.1的(1),有

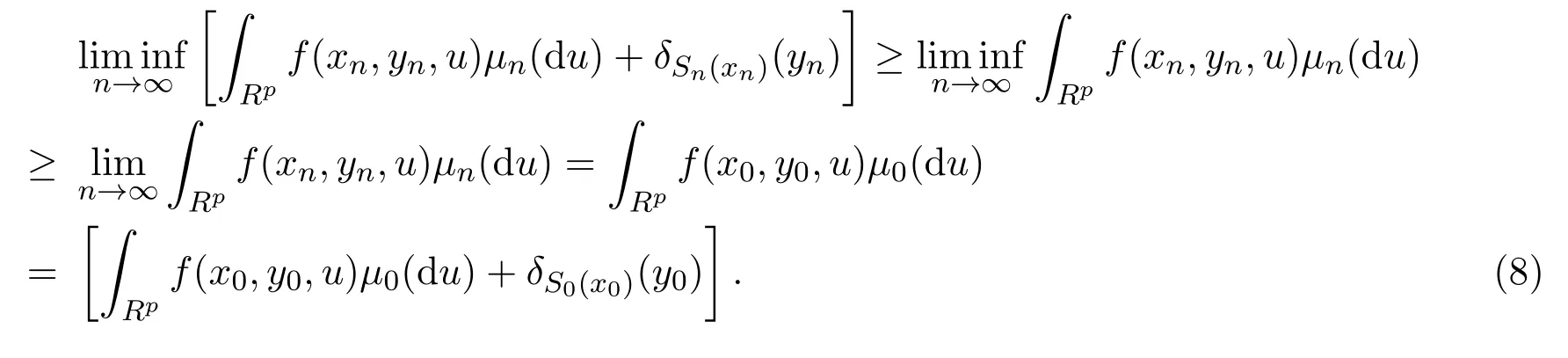
(ii)如果 y0S0(x0),且 yn→ y0,則存在 n0,當 n≥n0時,有 yn/∈Sn(xn),否則存在 {ynk}使得 ynk∈Snk(xnk),又由于 {yn}為收斂序列,則 ynk→ y0,又由引理 2.3的 (2)有,所以y0∈S0(x0),矛盾.于是有

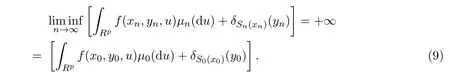
由(8)式和(9)式知(7)式成立.

其次,證明對任意y0∈Rm,存在某個yn→y0,使得(10)式成立.

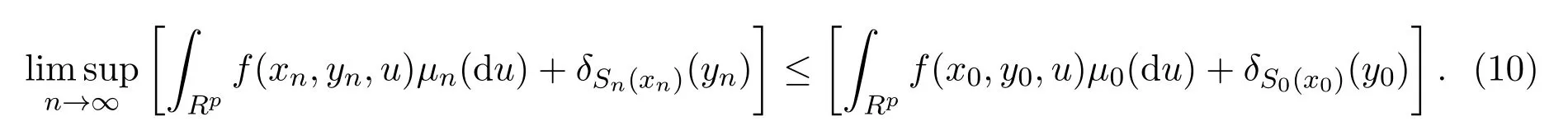
對y0∈Rm分兩種情況討論.

(i)如果 y0∈S0(x0),由引理 2.3的 (2),有則存在某 yn→ y0,使yn∈Sn(xn).由引理2.1的(1),有

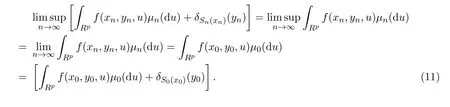
(ii)如果y0/∈S0(x0),對任意yn→y0,有

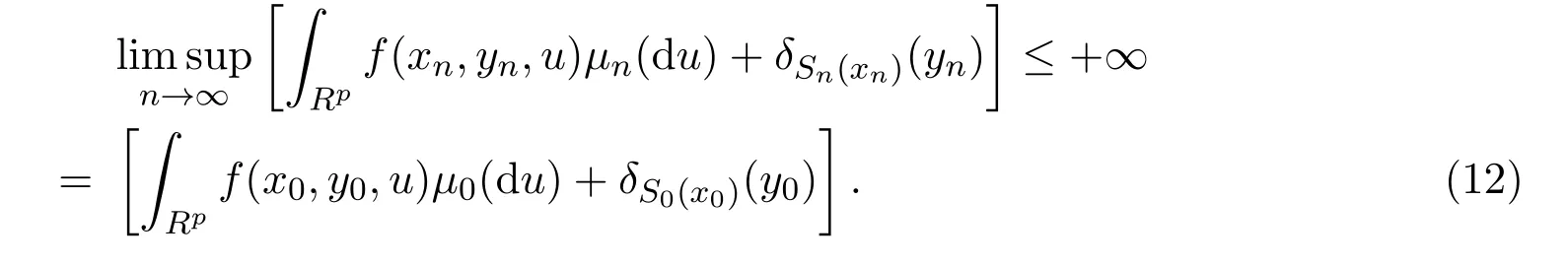
由(11)式和(12)式知(10)式成立.綜上可知結論成立.

集合A?Rn到集合B?Rn的上半距離定義為其中

定義 2.4[9]若xn→x0,稱集合序列{Mn(xn)}上半收斂于M0(x0),是指

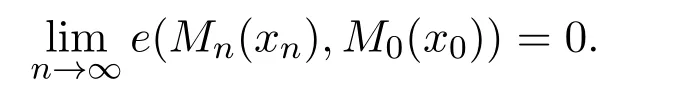
定理 2.1若xn→x0,且f(x,y,u)在X×Y×Rp上連續(xù)有界,gj(x,y,u),j=1,2,···,d,在 X×Y×Rp上下半連續(xù)且有界,對每個固定的 y,gj(x,y,u)關于 (x,u)上半連續(xù),可行集S0(x0)正則,且則問題(6)的最優(yōu)解集序列Mn(xn)上半收斂于問題(5)的最優(yōu)解集M0(x0).

證明由于S0(x0)正則,由引理2.1的(2)和引理2.3的(1)知,存在n0,當n≥n0時,

Mn(xn)?且M0(x0)/?.為了證明,即需證明:?ε>0,?N0,當n≥N0時,有e(Mn(xn),M0(x0))<ε,也即需證明:?ε>0,?N0,當n≥N0時,有

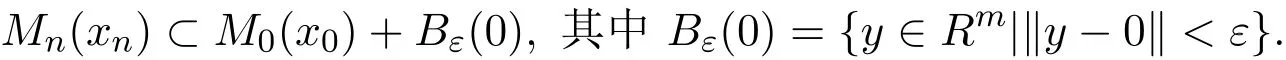
現(xiàn)證對任意包含M0(x0)的開集V,存在n0,當n≥n0時,有Mn(xn)?V.假設不成立,即存在nk,使得ynk∈Mnk(xnk)但ynk/∈V,而由于Mnk(xnk)?Y及Y的緊致性,則{ynk}必存在聚點y0,而V為開集,則y0/∈V.而另一方面,由引理2.4可得,y0∈M0(x0),即y0/∈V與M0(x0)?V矛盾,特別取V=M0(x0)+Bε(0),從而有

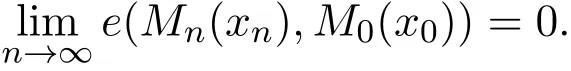
推論 2.1若xn→x0,且f(x,y,u)在X×Y×Rp上連續(xù)有界,gj(x,y,u),j=1,2,···,d,在 X×Y×Rp上下半連續(xù)且有界,對每個固定的 y,gj(x,y,u)關于 (x,u)上半連續(xù),可行集S0(x0)正則,且如果下層隨機規(guī)劃問題(5)有唯一最優(yōu)解,則問題(6)的任意一個最優(yōu)解yn(xn)∈Mn(xn)連續(xù)收斂于問題(5)的唯一最優(yōu)解y0(x0).

證明由定理2.1可知,問題(6)的最優(yōu)解集序列{Mn(xn)}上半收斂于問題(5)的最優(yōu)解集M0(x0).即?ε>0,?N0,當n≥N0時,有

其中 Bε(0)={y∈Rm|∥y?0∥<ε}.由于下層隨機規(guī)劃問題 (5)有唯一最優(yōu)解 y0(x0),即 M0(x0)={y0(x0)},且對任意的 yn(xn)∈Mn(xn),則由 (13)式可得,?ε>0,?N0,當n≥N0時,有

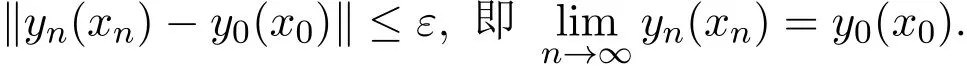
3 上層隨機規(guī)劃最優(yōu)解集的收斂性

設y0(x)是下層隨機規(guī)劃原問題(1b)的唯一最優(yōu)解,yn(x)是下層隨機規(guī)劃逼近問題(2b)最優(yōu)解集中的任意一個最優(yōu)解.則上層隨機規(guī)劃的原問題改寫為:

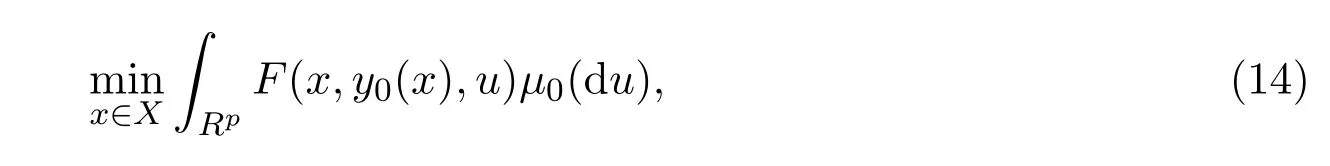
相應的逼近問題改寫為:

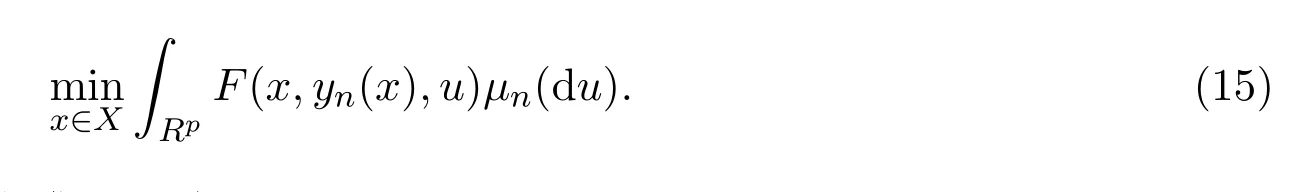
問題(14)和問題(15)的最優(yōu)解集分別為M0和Mn.

定理 3.1若xn→x0,且 F(x,y,u),f(x,y,u)在X×Y×Rp上連續(xù)有界,gj(x,y,u), j=1,2,···,d,在X×Y×Rp上下半連續(xù)且有界,對每個固定的y,gj(x,y,u)關于(x,u)上半連續(xù),可行集S0(x0)正則,且如果下層隨機規(guī)劃原問題(1b)有唯一最優(yōu)解,則

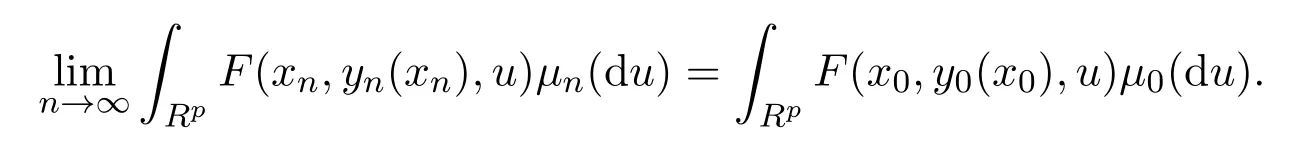
證明由推論2.1可知,當xn→x0時,yn(xn)連續(xù)收斂于y0(x0).此外,由于F(x,y,u)在X×Y×Rp上連續(xù)有界,所以對每個固定的u,有

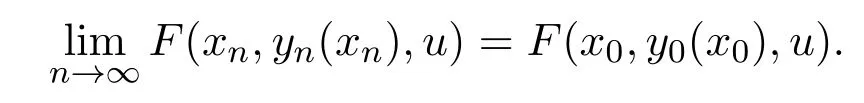
故由文獻[9]的定理5.1,有

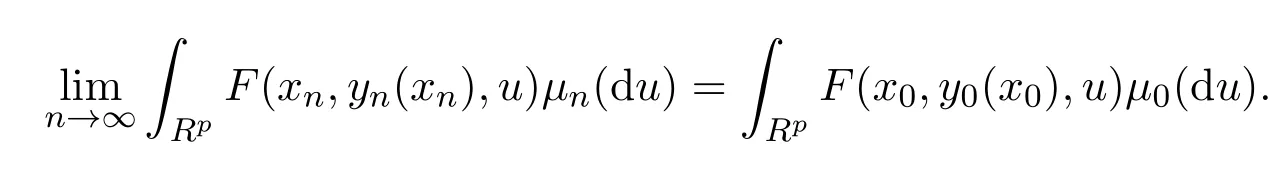
定理 3.2若F(x,y,u),f(x,y,u)在X×Y×Rp上連續(xù)有界,gj(x,y,u),j=1,2,···,d,在X×Y×Rp上下半連續(xù)且有界,對每個固定的y,gj(x,y,u)關于(x,u)上半連續(xù),對任意的x0∈Rn,可行集S0(x0)正則及X為緊集,且如果下層隨機規(guī)劃原問題(1b)有唯一最優(yōu)解,則問題(15)的最優(yōu)解集序列Mn上半收斂于問題(14)的最優(yōu)解集M0.

證明令Hn(x)=F(x,yn(x),u)μn(du).H0(x)=F(x,y0(x),u)μ0(du),應用定理3.1可知,當xn→x0時,有

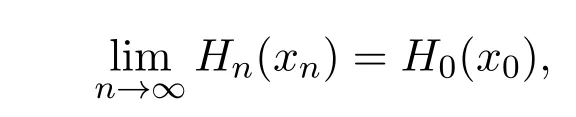
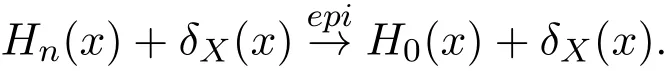
其余類似于文獻[9]的定理5.4證明.

[1]Wets R J B.Stochastic Programming[A].Handbook of Operations Research and Management Science[C]. Amsterdam:Elsevier Science Publisher,1989.

[2]駱建文,魯世杰.隨機規(guī)劃逼近解的收斂性[J].浙江大學學報,2000,27(5):493-497.

[3]Luo Jianwen.Stability analysis for stochastic optimization problems[J].Journal of Shanghai Jiaotong University,2007,12(5):684-687.

[4]Romish W,Schultz R.Stability analysis for stochastic programs[J].Annals of Operations Research, 1991,30(1):241-266.

[5]Dupatcova J,Growe-Kuska N,Romish W.Scenario reduction in stochastic programming:An approach using probability metric[J].Mathematical Programming,2003,95(3):493-511.

[6]霍永亮,劉三陽.隨機規(guī)劃逼近最優(yōu)解集的上半收斂性[J].西安電子科技大學學報,2005,32(6):953-957.

[7]萬仲平,吳國民,陳開周.一類二層規(guī)劃的上圖收斂性[J].運籌學學報,1998,2(24):48-53.

[8]萬仲平.關于二層規(guī)劃的逼近問題[J].系統(tǒng)科學與數(shù)學,2000,20(3):289-294.

[9]霍永亮.隨機規(guī)劃穩(wěn)定性理論[M].成都:西南交通大學出版社,2010.

The upper semi-convergence of the optimal solution set of approximation for bi-level stochastic programming

Zhou Wanna1,Huo Yongliang2,Wu Fan3
(1.College of Mathematics,Chongqing Normal University,Chongqing 401331,China; 2.College of Mathematics and Finance,Institute of Mathematics,Chongqing University of Arts and Sciences, Chongqing 402160,China; 3.Party Member and Concourse Department,Chongqing University of Arts and Sciences, Chongqing 402160,China)

A bi-level stochastic programming problem where the upper level stochastic programming is an optimization problem including a parametric unique optimal solution of the lower level stochastic programming, and the lower level stochastic programming is a parametric nonlinear programming including the decision variables of the upper level stochastic programming as parameters.This paper f i rst discusses the assumption that the lower level stochastic programming has unique optimal solution of the original problem,any approximation optimal solution sequence of the lower level stochastic programming converges to the unique optimal solution of the original problem.And then feedbacks the unique optimal solution of lower level stochastic programming to the upper level,obtains the upper semi-convergence of the upper level stochastic programming approximation optimal solution sequence.

Bi-level stochastic programming,optimal solution set,upper semi-convergence

O221.5

A

1008-5513(2014)02-0207-09

10.3969/j.issn.1008-5513.2014.02.013

2013-07-01.

重慶市教委科研基金(KJ091211);重慶高校創(chuàng)新團隊建設計劃項目(KJ301321).

周婉娜(1987-),碩士生,研究方向:隨機規(guī)劃穩(wěn)定性理論.

霍永亮(1965-),教授,研究方向:隨機規(guī)劃穩(wěn)定性理論.

2010 MSC:90C30