數控機床定位誤差全溫度綜合建模及實時補償*

朱小龍，楊建國，代貴松

(上海交通大學 機械與動力工程學院，上海 200240)

數控機床定位誤差全溫度綜合建模及實時補償*

朱小龍，楊建國，代貴松

(上海交通大學 機械與動力工程學院，上海 200240)

提出一種數控機床定位誤差的全溫度綜合建模方法。通過測量獲得加工中心定位誤差，采用多項式擬合和縱向建模法建立了加工中心在不同溫度狀態下定位誤差的綜合預測模型。利用FANUC數控系統的外部原點偏移功能，對一臺加工中心進行實時誤差補償實驗驗證。實驗結果表明，應用此誤差建模方法及補償功能，在常溫和溫升狀態下，加工中心在三個方向的定位誤差與補償前相比都下降90%左右，大幅提高了加工中心在變溫狀態下的定位精度。

加工中心；定位誤差；誤差建模與補償

0 引言

高精密加工在當今工業應用中占有舉足輕重的作用，已經成為國際競爭力的重要標志。在機械加工過程中，機床的誤差將會直接影響工件的加工精度。定位誤差是影響機床精度的重要因素之一[1]。考慮到機床溫度場對定位精度影響較大[2]，因此對機床不同溫度狀態下的定位誤差進行研究是極其有意義的。

機床溫度和定位誤差檢測的目的是為了獲取機床溫度場和變形位移場的信息，建立定位誤差預測模型并對定位誤差實時補償提供理論依據。通常誤差補償是在某一溫度下建立的誤差預測模型基礎上進行的，而沒有考慮到由于機床溫度的變化引起的機床定位誤差變化，這也就是為什么一般補償的效果不明顯[3]。因此需要對機床各種溫度條件下的定位誤差建模問題作進一步的研究。

本文使用激光干涉儀對一臺加工中心從常溫到熱平衡狀態的全溫度條件下的定位誤差進行了測量，并運用線性擬合及縱向建模綜合建模方法對一臺加工中心的定位誤差進行建模，從而建立了對加工中心定位誤差的高精度綜合預測模型。最后在加工中心上，基于FANUC數控系統的外部原點偏移功能，對加工中心常溫及溫升狀態下的定位誤差進行實時誤差補償實驗。在加工中心上的誤差實時補償實驗表明，文中采用的誤差建模方法及實時補償功能能夠大幅提高加工中心的定位精度。

1 誤差測量

加工中心移動軸定位誤差的測量采用激光干涉儀，如圖1所示。為了減少測量過程中的隨機誤差，對每個軸的定位誤差分別重復測量三次，并取測量的平均值作為最終定位誤差的測量結果[4]。加工中心主軸最大轉速8000rpm，快速進給速度33m/min，X/Y/Z軸行程分別為850/560/650mm。

圖1 定位誤差的測量

本文以加工中心X軸定位誤差的測量、建模為例進行說明。考慮到數控加工中心在不同溫度下的定位誤差是不同的[5-6]，因此必須測量加工中心在不同溫度下的定位誤差及溫度。在采用激光干涉儀對加工中心的定位誤差進行測量時，同時測量加工中心關鍵點的溫度，使得每一組關鍵點的溫度對應一組定位誤差。在實驗測量過程中加工中心空運行，主軸轉速40000rpm，X/Y/Z軸進給速度為f=0.2mm/r。為了測量關鍵點溫度，將2個PT100溫度傳感器加工中心上，其中T1測量X軸絲杠螺母溫度，T2測量X軸導軌溫度[7]。圖2為溫度傳感器(白色圓圈)實際布置圖。

圖2 X軸溫度傳感器的布置

實驗中測量數控加工中心從冷態(即剛開機，常溫狀態下)到熱平衡過程中的定位誤差及關鍵點溫度，實驗一共采集到七組數據。實驗測得的加工中心在不同檢測時間下的加工中心關鍵點溫度以及定位誤差如圖3所示。

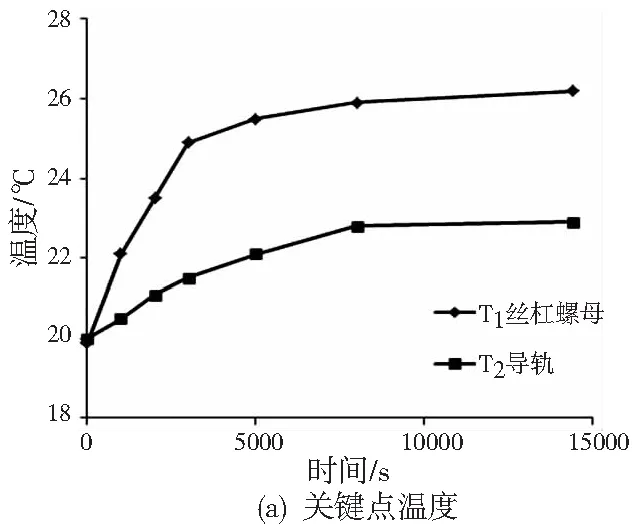
圖3 加工中心X方向關鍵點溫度和定位誤差

2 誤差建模

由圖3可見，在不同的溫度狀態下，加工中心的定位誤差分布有很大的變化，且加工中心到達熱平衡時間大概在8000s左右。圖3可以看出，加工中心在不同的溫度下，X方向的定位誤差是不同的，有明顯的變化，這也就是為什么實際切削過程中一般誤差補償效果不太明顯的原因。因為其補償主要是常溫下的定位誤差，而在實際切削加工過程中，定位誤差是隨機床溫度場變化而變化的。如圖3所示，加工中心定位誤差隨著關鍵點溫度和坐標位置的變化而變化，是一種與機床坐標和機床溫度有關的誤差。考慮到不同時刻，定位誤差是與溫度相關的，將機床定位誤差被分為兩類：與位置有關的定位誤差，與位置無關的定位誤差[8-9]。與位置無關的定位誤差，是由于機床溫度場的作用，而與位置有關的定位誤差則是溫度和位置的綜合作用。考慮到這些原因，需要建立不同的模型來預測機床定位誤差。與位置無關的定位誤差可以按公式(1)表示：

(1)

式中E1(t)代表與位置無關的定位誤差，t代表時間，βi為系數，i代表溫度傳感器編號，Ti(t)表示t時刻下編號為i的溫度傳感器的溫度，N代表溫度傳感器的數目。

與位置有關的誤差可以表示為公式(2)：

(2)

式中E2(t)代表與位置有關的定位誤差，x為對應相應定位誤差的位置。

如果僅僅考慮定位誤差與溫度的關系，則公式(1)和(2)中E1和E2與溫度變量成線性關系，所以可以將公式(1)和(2)合并為：

E=TB

(3)

式中T=[T1(t),T2(t),...,TN(t)]為溫度變量矩陣，即在不同時刻下采集的溫度數據組，B為相關系數矩陣，可以通過最小二乘法獲得。

以X方向為例，采用縱向建模法，即在某一確定的位置x處，對此處隨機床溫度變化引起的定位誤差進行建模。由于在相同位置處，位置對定位誤差的影響是相同的，從而按此方法建模時，就可以先不考慮位置對定位誤差的影響。故可對某一位置在不同溫度下的定位誤差按公式(1)進行建模。以X方向的測量中間點x=400mm和最遠端x=800mm處的定位誤差為例，進行誤差建模，可以得到如下定位誤差模型：

E400=2.4258T1-2.1313T2

(4)

E800=4.7416T1-3.9864T2

(5)

位置x=400mm和x=800mm處定位誤差擬合曲線如圖4所示。由x方向x=400mm和x=800mm處定位誤差擬合曲線可以看出，上述縱向建模法建立的模型可以很好的對定位誤差進行擬合建模，且曲線擬合殘差都在很小的范圍之內，滿足建模的精度要求。

圖4 曲線擬合

同樣在X方向的其它位置，分別對定位誤差進行縱向建模，可以得到X方向的建模系數如下表1所示。

表1 X方向定位誤差建模系數

由表1可以看出，誤差擬合曲線中的系數α1、α2，在機床沿x方向運動時，呈線性變化，其中α1隨x變大而變大，α2隨x變大而變小。因而建模系數α1、α2可以分別對x進行一次擬合，擬合結果分別為：

α1=0.00585x+0.0202

(6)

α2=-0.00479x-0.0476

(7)

擬合曲線如圖5所示。可以看出，對誤差擬合曲線中的系數α1、α2進行線性擬合是合適的，一次擬合的模型能夠滿足建模的要求。

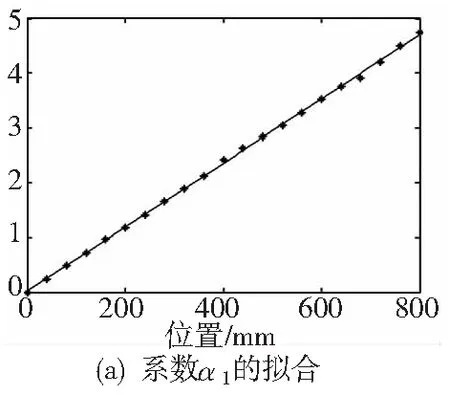
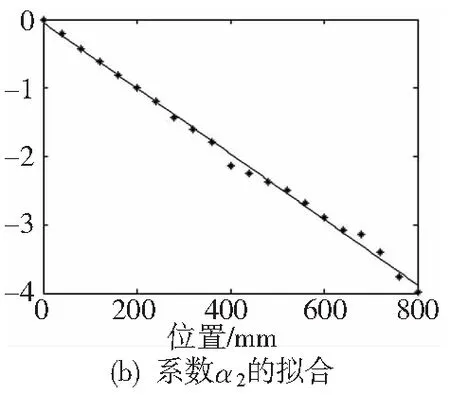
圖5 X方向系數的擬合

綜合考慮機床溫度和位置的影響，根據公式(3)可以得到加工中心X方向在任意位置處，不同溫度下的定位誤差可以表示為：

Ex=(0.00585x+0.0202)T1+(-0.00479x-0.0476)T2

=[0.0202T1-0.0476T2]+[0.00585xT1-0.00479xT2]

(9)

將從常溫狀態開始測量定位誤差的7次實驗的次數作為坐標軸的x軸坐標，移動軸的位置作為y軸坐標，不同溫度狀態下的定位誤差作為z軸坐標，繪制如圖6所示示意圖，則采用的誤差模型的擬合效果如圖6a所示。實驗有7條誤差曲線，共有21×7=147個誤差數值，匯總這些誤差，其中前21個點為常溫下模型擬合殘差點，后面以此類推[10]。則X方向定位誤差殘差示意圖如圖6b所示，可以看出采用模型的建模精度在[-1.72μm，2.16μm]范圍內。

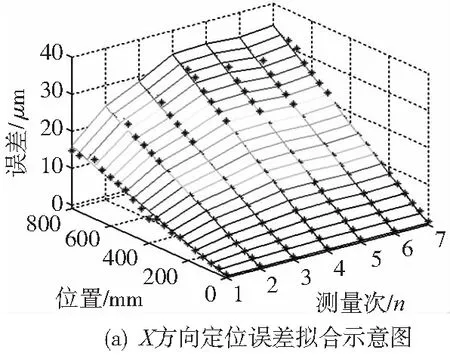
圖6 X方向定位誤差建模

3 實驗

3.1 補償原理

為了驗證模型的有效性，在一臺加工中心上進行了誤差補償實驗，補償實驗基于FANUC 數控系統的外部坐標原點偏移功能。實驗中將不同溫度狀態下定位誤差預測模型計算得到的誤差值，通過機床數控系統外部坐標偏移功能加到系統控制信號中，從而實現機床誤差的實時補償[11]。數控系統的外部坐標偏移功能無需修改機床的數控指令，只要在系統PLC中添加部分程序即可，且不會影響原系統。圖7為補償原理框圖。

圖7 補償原理圖

3.2 補償實驗

將上述方法應用于一臺加工中心上，采用激光干涉儀測量加工中心常溫狀態以及溫升狀態下補償前后的定位誤差，并對補償前后效果進行比較。實驗結果如圖8所示。圖8可以看出，上文所提誤差建模方法可以準確的預測數控機床在不同溫度及不同位置下的定位誤差，也就是建立了加工中心從常溫狀態到熱平衡狀態下的定位誤差預測模型。以X方向為例，補償后，加工中心常溫下最大定位誤差由38.3μm下降至4.5μm，誤差降低了88.2%左右；溫升后最大定位誤差由28.6μm下降至3.0μm，誤差下降89.4%左右。總的來說，加工中心在常溫及溫升狀態下，誤差補償后與補償前相比，三個方向的定位誤差都下降90%左右，大幅提高了機床的精度。

圖8 常溫及溫升補償前后對比

4 結論

(1)加工中心定位誤差建模中使用的多項式擬合及縱向建模法，對加工中心從常溫到熱平衡的全溫度下的定位誤差進行建模，獲得了高精度的定位誤差綜合預測模型。采用這種建模方法，可以準確的預測機床處于任意溫度狀態及任意位置處的定位誤差，且具有良好的魯棒性。

(2)在加工中心上基于FANUC數控系統外部原點偏移功能的實時誤差補償實驗表明，此方法具有較好的補償效果，能夠在機床溫度變化狀態下大幅提高機床精度。

[1] 王福吉，賈振元，陽江源，等. 基于動態模糊神經網絡的機床時變定位誤差補償[J].機械工程學報，2011,47(13):175-179.

[2] Wei Wang，Yi Zhang，Jianguo Yang，et al. Geometric and thermal error compensation for CNC milling machines based on Newton interpolation method[J]. Journal of Mechanical Engineering Science，2012,0(0):1-9.

[3] ABDUL W K，CHEN Wuyi. Systematic geometric error modeling for workspace volumetric calibration of a five-axis turbine blade grinding machine[J]. Chinese Journal of Aeronautics，2010,23:604-615.

[4] DU Zhengchun，ZHANG Shujie，Hong Maisheng. Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder[J]. International Journal of Machine Tools & Manufacture, 2010, 50: 270-280.

[5] Sina Eskandari，Behrooz Arezoo，Amir Abdullah. Positional,geometrical,and thermal errors compensation by tool path modification using three methods of regression,neural networks,and fuzzy logic[J]. International Journal of Advanced Manufacturing Technology. 2013,65:1635-1649.

[6] 崔崗衛，高棟，姚英學. 重型數控機床熱誤差的分離與建模[J]. 哈爾濱工業大學學報，2012，44(9):51-56.

[7] Kaiguo Fan，Jianguo Yang，Liyan Yang. Orthogonal Polynomials-based thermally induced spindle and geometric error modeling and compensation[J]. International Journal of Advanced Manufacturing Technology,2013,65:1791-1800.

[8] Jie Zhu，Jun Ni，Albert J. Shih. Robust Machine Tool Thermal Error Modeling Through Thermal Model Concept[J].Journal of Manufacturing Science and Engineering, 2008,130:061006.

[9] J. S. Chen，J. X. Yuan，J. Ni，et al. Real-time Compensation for Time-variant Volumetric Errors on a Machining Center[J].Journal of Manufacturing Science and Engineering，1993,115 (4):472-479.

[10]王維，楊建國，姚曉棟，等.數控機床幾何誤差與熱誤差綜合建模及實時補償[J]. 上海交通大學學報,2012,48(7):165-179.

[11]沈金華，李永祥，魯志政，等. 數控車床幾何與熱誤差綜合實時補償方法應用[J].四川大學學報，2008,40(1):163-166.

(編輯 李秀敏)

Synthesis Modeling and Real-time Compensation of Position Errors at Full Temperature for Machine Tools

ZHU Xiao-long，YANG Jian-guo，DAI Gui-song

(School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240,China)

A synthesis model of positioning error under full temperature for machine tools is presented. Through measuring the positioning error of machining center, a synthesis prediction model for positioning error at different temperatures is proposed based on polynomial fitting and longitudinal modeling. Real-time error compensation is carried out on a machining center by applying the external coordinate offset function of FANUC computer numerical control(CNC) system. The real-time compensation carried out on the machining center shows that application of this compensation method compensates positioning errors in three directions by almost 90% compared with no compensation. The accuracy of the machining center is improved effectively.

machining center；positioning error；error modeling and compensation

1001-2265(2014)05-0083-04

10.13462/j.cnki.mmtamt.2014.05.021

2013-09-06

國家自然科學基金(51275305);高等學校博士學科點專項科研基金(20110073110041)

朱小龍(1988—)，男，江蘇東臺人，上海交通大學碩士研究生，研究方向為數控機床精密加工與測試，(E-mail)wolloy0504@126.com。

TH164;TG659

A