滾珠絲杠副載荷分布情況研究

張陳靈，范元勛

(南京理工大學 機械工程學院，江蘇 南京 210094)

滾珠絲杠副載荷分布情況研究

張陳靈，范元勛

(南京理工大學 機械工程學院，江蘇 南京 210094)

滾珠絲杠副受外載荷作用時滾珠的受力是比較復雜的，但目前在研究滾珠絲杠副滾珠受力時都是簡單地按照均載來分析，這與實際的載荷分布情況有較大的偏差。建立一個變形協調條件下的滾珠絲杠副載荷分布的模型，并分析了幾何誤差對滾珠受載的影響。

滾珠絲杠副；載荷分布；幾何誤差

0 引言

滾珠絲杠副作為一種新型的螺旋傳動元件，由于其高精度、高效率、優越的耐磨損性和高速特性以及運動可逆性等良好的機械性能，它在國內外工程技術界已經獲得了廣泛的應用，尤其是近年來其在航空工業的各個部門更是獲得了高度的重視。而研究滾珠絲杠副的載荷分布情況是研究其一系列機械性能的基礎。但是，目前在研究滾珠絲杠副載荷分布時都是簡單地按照滾珠均勻受載來分析，這與實際的載荷分布情況有較大的偏差。因此，建立一個求解滾珠絲杠副載荷分布的模型顯得十分必要。

1 數學模型的建立

1.1 滾珠絲杠副滾珠等效受力模型的研究

首先對單螺母滾珠絲杠副在絲杠受拉和螺母受壓狀態下(以下簡稱T-C狀態)的受力進行分析，如圖1所示。圖中Fa0為滾珠絲杠副的軸向外載荷；Ds為絲杠的外徑；Dn為螺母的外徑；Fsi，Fni為絲杠和螺母對第i個球的軸向力。

為了有效地分析滾珠與滾道接觸時的受力情況，將某個滾珠和滾道接觸時的狀態放大，如圖2所示。圖中βj為第j個滾珠和滾道間的接觸角(j=1,2,3,…)；Pj為第j個滾珠所受的法向載荷db為滾珠的直徑；t為曲率比。

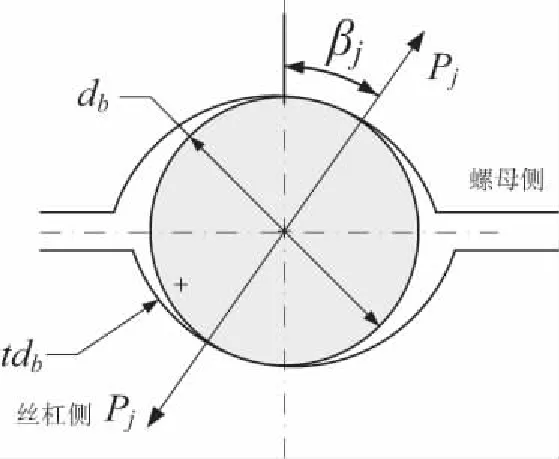
圖2 滾珠在滾道中的接觸狀態圖

為了方便分析，結合圖1和圖2建立一個如圖3所示滾珠絲杠副滾珠等效受力的模型圖，它清楚地顯示了滾珠和滾道的接觸狀態。

圖3 滾珠絲杠等效受力分析圖

根據平衡受力情況和赫茲理論，絲杠和螺母對第i個球的軸向力，Fsi和Fni，可以由式(1)得來：

(1)

式中：Fa0——所受的軸向載荷；

Pj——第j個滾珠所受的接觸力；

λ——滾珠絲杠的螺旋角。

由滾珠軸向外載荷和滾珠間的作用力關系可得：

(2)

式中：Z——滾珠的個數；

Pjsinβjcosλ——第j個球和滾道間接觸力的軸向投影。

式(2)就是得到的軸向外載荷與每個滾珠法向載荷之間的關系。

1.2 考慮誤差情況下變形協調關系的建立

在分析了滾珠絲杠副滾珠受力狀態之后，來考慮滾珠受力時的變形情況。如圖4所示，為了簡化分析，把第i個滾珠，i-1個滾珠，螺母和絲杠軸的延螺旋角方向的接觸狀態放大出來。

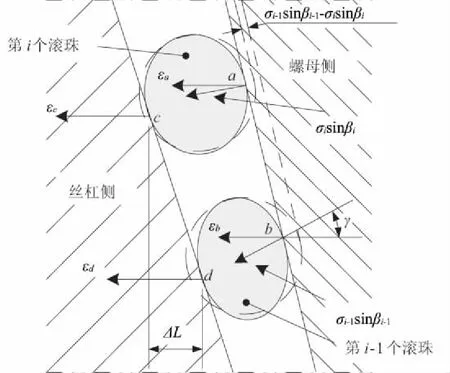
圖4 第i個滾珠和第i-1個滾珠在螺旋角方向的接觸狀態圖

接下來研究滾珠受力時的變形協調關系。首先，給絲杠提供一個軸向力，這個軸向力使所有的滾珠都保持T-C狀態。實際受載后，滾珠及滾道的幾何誤差(主要是滾珠的直徑誤差、絲杠副的導程誤差)會導致的滾珠接觸位置有所偏移。假設由于幾何誤差導致的所有接觸位置誤差不會改變初始的接觸角。如圖4所示，空間變形量在螺旋角的平面內。在接觸點a和b，幾何誤差分別為σisinβi，σi-1sinβi-1。

圖5顯示的是絲杠單元的受力變形分析。ΔL表示第i個滾珠和i-1個滾珠間的距離。第i個球和滾道的接觸點a和c的變形量εa和εc，它們會隨著滾珠絲杠的軸向變形而改變。同樣的，還有第i-1個球和滾道的接觸點b和d的變形量εb和εd。

圖5 絲杠單元變形受力分析圖

在T-C狀態下，絲杠c點和d點之間的軸向位移變化量是εsi，螺母a點和b點之間的軸向位移變化量是εni。他們可以由式(3)和式(4)得到：

εsi=εc-εd

(3)

εni=εb-εa

(4)

結合上述兩式，可以得到滾珠的變形協調關系，即：

εsi=(εc-εa)-(εd-εb)-εni

(5)

這里(εc-εa)和(εd-εb)分別是第i個球和i-1個球的軸向變形。當第i個滾珠及i-1個滾珠和滾道接觸時，相應軸向變形將抵消絲杠的幾何誤差σisinβicosλ，σi-1sinβi-1cosλ和滾珠接觸變形的軸向投影δisinβicosλ和δi-1sinβi-1cosλ，這就是所要研究的位移協調理論。將他們代入式(5)，就可以得到考慮誤差情況下的變形協調條件：

εsi=[δi-1sinβi-1-δisinβi-

(σi-1sinβi-1-σisinβi)]cosλ-εni

(6)

式(6)就是滾珠在考慮誤差情況下變形協調關系。

1.3 滾珠受載模型的建立

本小節根據誤差情況下的變形協調條件，建立滾珠受載分布的模型，假設滾珠絲杠副每個滾珠的接觸角在每一時刻都相等。根據式(6)可得：

(7)

式(7)中，δi、δi-1是第i個滾珠及i-1個滾珠和滾道接觸時，相應接觸變形變形量，(σi-1-σi)為誤差項。對于間距ΔL內的絲杠軸和螺母在T-C狀態下得變形量εni和εsi可以由式(8)和式(9)得到：

(8)

(9)

這里En，Es分別為絲杠和螺母的彈性模量。An，As分別為絲杠和螺母的有效截面區。假設絲杠的導程為L，每個導程內的滾珠數為M，則兩個滾珠間的軸向平均距離ΔL為：

(10)

由于主要的接觸曲率隨著方向變化，而且接觸區是一個橢圓，所以形變量δ可以由赫茲彈性接觸理論得到：

(11)

這里K為常數，它是由接觸點的主曲率半徑，材料的彈性系數等決定。

將式(1)、式(8)、式(9)和式(11)代入式(6)中得：

(12)

假設每個滾珠的接觸角都相等，則式(12)化為：

(13)

式(13)反映了第i個滾珠及第i-1個滾珠法向接觸載荷Pi與Pi-1的關系，其中(σi-1-σi)為誤差項，接觸角β與螺旋升角λ都是已知的，而其他參數K，εsi，εni都是可以通過上述相應的計算式得出的。

因此，式(2)與式(13)組成了滾珠絲杠副變形協調條件及幾何誤差下的載荷分布模型，即：

(14)

這個滾珠受載模型可以運用牛頓迭代法計算得到，通過計算出每個滾珠的受載情況，就可以分析出整個滾珠絲杠滾珠的受載分布情況。

此外，上述模型是滾珠絲杠副在絲杠受拉和螺母受壓狀態時(即T-C狀態)的建立分析的。當然，其他外部載荷條件(如假設單螺母和絲杠都承受張力)的非線性方程也可以根據上述的方法構造建立。

2 滾珠受載實例計算與誤差分析

2.1 無誤差時滾珠受載分析

現就滾珠絲杠副滾珠載荷分布問題，進行了載荷分布的理論計算與推導，舉例對某型號滾珠絲杠副的滾珠受載進行計算。各項參數如下：絲杠公稱直徑d0=16mm，螺母外徑Ds=30mm,滾珠直徑db=3.175mm，導程L=4mm，滾道曲率半徑和滾珠半徑之比t=1.04，滾珠圈數n=4，每個滾珠的接觸角β0=45°，螺旋升角λ=4.55°，工作滾珠總數Z=52，軸承鋼的彈性模量E=2.07×105MPa，泊松比μ=0.29，且給螺母施加30kN的軸向外載荷。

由式(10)得兩個滾珠間的軸向平均距離ΔL為：

絲杠和螺母有效截面積為：

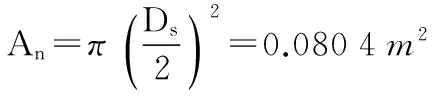
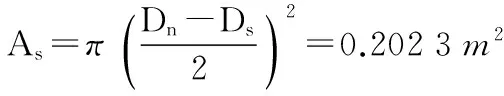
計算K，由查文獻[1]可知:

(15)

計算滾珠與滾道面出的曲率和∑ρ

由Kn的值得則式(12)中Kp的值：

當滾珠直徑無誤差時，式(15)迭代方程中σi-1-σi=0，式(14)模型可變為：

(16)

運用牛頓迭代法計算出每個滾珠的受載情況，求得最大法向接觸載荷P1= 0.928kN，最小法向接觸載荷P52=0.711kN。以滾珠數為橫坐標，第i個滾珠法向載荷Pi與最小載荷P52之比為縱坐標，得到滾珠絲杠副的載荷分布情況。

為了驗算本模型計算結果的準確性，以滾珠數i為橫坐標，第i個滾珠接觸載荷與最小接觸載荷之比Pi/Pmin，將本模型在無誤差情況的計算結果和半螺距模型[2]進行比較，初始的接觸角β0=45°。

在T-C狀態的情況下，半導程模型和本文模型的比較結果如圖6所示。由圖可知，第i個滾珠的接觸載荷隨著i的增大而呈減小的趨勢。而且，本模型滾珠的負載分布曲線介于半螺距模型曲線之中，這表明本模型計算結果與半導程模型結果是吻合的。

圖6 無誤差情況下本模型和半螺距模型滾珠載荷分布情況圖

2.2 滾珠幾何誤差對載荷分布的影響

2.2.1 滾珠幾何誤差的計算分析

圖4所示的，滾珠幾何誤差可以轉化成本模型所計算的誤差。在本文建立的模型中，滾珠幾何誤差對載荷分布的影響是可以分析計算的。

絲杠滾珠的直徑誤差實際上是一種隨機誤差，很難分析，但是在一定的統計范圍內誤差對滾珠受載的影響是可以分析的。假設給定一組滾珠的直徑誤差，如圖7所示，該組平均幾何誤差為-2μm。對于滾珠直徑誤差的分析，Masaomi Tsutsumi等[6]結合數值實驗的結果分析指出，對于一組隨機誤差的滾珠直徑，當誤差的平方差Sd≤5μm時，滾珠所受的法向載荷變化量ΔP≤1N(不到1%的變化量)。因此當給定一組誤差的平方差Sd≤5μm時，，由于誤差隨機性引起的載荷變化量可以忽略，可以直接用平均幾何誤差來代替計算。

圖7 負誤差情況下滾珠載荷分布情況圖

當滾珠平均幾何誤差為-2μm時，式(15)迭代方程可以轉化為：

(17)

這樣聯立式(17)迭代方程和式(2)即可以求出所有滾珠的接觸載荷。

同理可以分析求出滾珠平均幾何誤差分別為+1μm，+2μm，-4μm時的滾珠受載情況。

2.2.2 誤差對滾珠受載的影響分析

現研究誤差對滾珠載荷分布的影響。首先，假設位于絲杠中間的第i個滾珠的直徑誤差是負誤差，對于不同的負誤差，計算出每個滾珠的接觸載荷。我們來研究當誤差σi-1-σi=-2um和σi-1-σi=-4um兩種負誤差情況下的滾珠接觸載荷分布情況。首先計算出每個載荷Pi與最小載荷P52之比，然后再畫出載荷分布圖，載荷分布圖如圖7所示。由圖可知，第i個滾珠的接觸載荷呈減小的趨勢，減少的量與誤差的比例有關。從圖中還可以得出結論，滾珠絲杠副工作滾珠中的載荷會隨著負誤差的增加而增加。

接下來，再研究誤差σi-1-σi=+1um和σi-1-σi=+2um兩種正誤差情況下的滾珠接觸載荷分布情況。同樣地計算出每個載荷Pi與最小載荷P52之比，畫出載荷分布圖，載荷分布圖如圖8所示。從圖中可以得出結論，滾珠絲杠副工作滾珠的載荷隨著正誤差的增加而減少。

圖8 正誤差情況下滾珠載荷分布情況圖

3 結論

根據以上絲杠幾何誤差對滾珠絲杠載荷分布影響的分析，可以得出以下結論：

1) 本文提出的滾珠絲杠機構載荷分布計算模型可以用來計算滾珠幾何誤差在一定分布規律內的滾珠載荷。

2) 接觸位置的負誤差會導致滾珠在該位置的赫茲接觸載荷的減小，正誤差會導致載荷的增加，增加量和減小量與絲杠其他滾珠共同分擔。

3) 上述中一些運用于單螺母結構的結論也適用于雙螺母結構。

[1] T.A.Harris，滾動軸承分析[M](1、2卷),北京：機械工業出版社，1967.

[2] M. Izawa， H. Shimoda， Study on the load distribution in the ball screw，Japan Journal of Precision Machine 42 (11) (1976) 1021-1028.

[3] 程光仁,施祖康,張超鵬.滾珠螺旋傳動基礎[M].北京:機械工業出版社,1987.

[4] 萬長森.滾動軸承的分析方法[M]. 北京:機械工業出版社,1987.

[5] 饒振綱,王勇衛.滾珠絲桿副及自鎖裝置[M].北京:國防工業出版社,1990.

[6] Masaomi Tsutsumi, Xuesong Mei, Study on the load distribution of ball screws with errors, Mechanism and Machine Th- -eory 38 (2003) 1257-1269.

Research on Load Distribution of Ball Screw

ZHANG Chen-ling，FAN Yuan-xun

(College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

The stress of the ball is complicated when the ball screw is loaded by external force.However, the ball load is analyzed simply according to the average load distribution when its load distribution is researched on. This is large different from the actual load distribution. A model is developed to analyze its load distribution and geometry errors which have influence on its load disfribution.

ball screw; load distribution; geometry errors

張陳靈(1988-)，男，江蘇南通人，碩士研究生，研究方向為機械電子工程。

TH133.2

A

1671-5276(2014)02-0006-04

2013-01-17