基于頻率響應法的后視鏡振動光學穩定性優化

趙婷婷 汪霞 王昌富

（泛亞汽車技術中心有限公司）

基于頻率響應法的后視鏡振動光學穩定性優化

趙婷婷 汪霞 王昌富

（泛亞汽車技術中心有限公司）

為了解決某項目后視鏡光學穩定性試驗中出現的失效問題，采用基于頻率響應法的CAE方法模擬了光學穩定性試驗。建立了頻率響應分析流程，通過試驗和仿真結果對比可知，采用頻率響應分析得出的共振頻率與位移響應差異較小，準確再現了失效問題，并提出了相應的改進方案。通過試驗驗證了分析方法的準確性和改進方案的有效性。

1 前言

在車輛行駛過程中，路面激勵、發動機和傳動系統的振動激勵都會引起車身振動，進而造成后視鏡產生一定程度的振動，嚴重的振動會造成后方視野模糊不清，導致駕駛員因判斷失誤而引發事故[1]。

后視鏡振動光學穩定性一般由臺架振動試驗評估，目前沒有成熟的CAE仿真方法模擬該試驗。本文結合某一項目后視鏡試驗失效案例，對該性能進行了CAE方法研究和對標，通過試驗對后視鏡優化效果進行了驗證。

2 后視鏡振動光學穩定性試驗

光學穩定性試驗常用的設計要求是垂直加速度0.5 g時，后視鏡偏移角小于0.13°。

2.1 失效案例

在后視鏡光學穩定性試驗中，將后視鏡安裝在模擬實車安裝狀態的夾具上，對其施加一個垂直加速度為0.5 g的激勵，頻率在20～250Hz之間，同時向鏡面發射激光束，光線經后視鏡反射后到達目標靶。激光束由振動改變而產生的偏移角用距離1720 mm的目標靶上測得位移值來表現。

在某后視鏡研發過程中，后視鏡振動光學穩定性試驗失效。12個樣本平均共振頻率為66 Hz，光斑平均位移值為11 mm，即平均振動角度為0.18°，超出設計目標值。

2.2 試驗原理和仿真分析技術路線

后視鏡抖動主要包括后視鏡自身運動副造成的抖動和后視鏡本身剛度不足引發的抖動，且后視鏡自身運動副通常是后視鏡抖動的主要原因。因此，首先檢查了運動副的設計狀態，加強運動副剛度后再次進行試驗，發現試驗結果基本無變化。因此，本文主要關注后視鏡本身的剛度。

該后視鏡鏡面曲率半徑r=1 200 mm左右，遠大于鏡面尺寸，本文將球面鏡簡化為平面鏡。根據光的反射原因，可將光斑大小轉換為后視鏡自身的抖動幅值，如圖1所示，其中，反射光線的夾角等于法線夾角的2倍。

圖1中，O為后視鏡的固定約束點，根據幾何關系可以得出以下公式:

式中，θ1為鏡面繞固定點轉動角度，即后視鏡鏡面法向夾角；θ2為后視鏡鏡片中心的偏移角，即反射光線夾角；d為后視鏡鏡面振動位移；d為目標靶上的振動位移；L1為后視鏡鏡片中心到固定約束點的距離；L2為后視鏡鏡面中心到目標靶的距離。

本文采用頻率響應分析方法來再現試驗。由于后視鏡結構比較復雜，內部存在運動副，而且其材料多為各向異性的塑料，因而后視鏡有限元模型需要和試驗不斷對標調整。圖2詳細描述了本文的技術路線。

3 仿真分析和試驗對標

3.1 后視鏡有限元模型的建立

后視鏡由10余個零件組裝而成，主要結構及材料如圖3所示。在Hypermesh的OptiStruct模塊下建立后視鏡的有限元模型，其中，護罩、鏡殼、鏡框、裝飾罩和鏡托板及鏡片等厚度均勻的零件采用殼單元建模，單元基本尺寸為3mm；支座、基板和密封圈等采用體單元建模，為了更好的表達加強筋、倒角和卡扣等處的結構特征，本文采用了四面體單元，單元基本尺寸為1 mm。RBE2單元用來模擬各個卡扣和螺栓連接。全部模型有759826個單元，有限元模型如圖4所示。

后視鏡在承受車身縱向載荷時可以繞銷軸轉動，銷軸局部結構如圖5所示。銷軸內部有螺旋彈簧，通過銷軸連接支座和基板。由于后視鏡在垂向激勵情況下銷軸不發生轉動，本文中的有限元模型將銷軸的轉動副固接，以簡化模型。

表1給出了后視鏡結構材料的主要性能參數。

表1 材料性能參數表

3.2 有限元模型的模態驗證

為了驗證模型的準確性，在后視鏡與車身連接處約束全部自由度進行模態分析，前3階頻率值與振型如圖6所示，與試驗對比結果如表2所列。

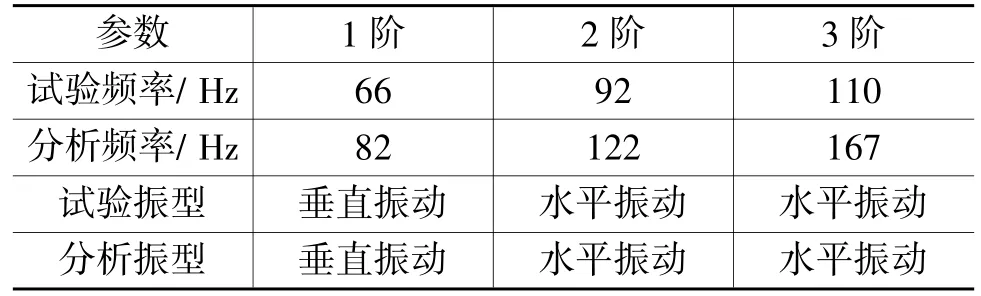
表2 模態仿真與試驗對比結果

根據表2可知，后視鏡仿真振型與試驗振型基本一致，但仿真頻率值明顯大于試驗值，即后視鏡仿真模型比實際結構剛度偏大。

3.3 模態分析模型的影響因素研究

根據模態基礎理論可知，系統質量越大，模態頻率越小；系統剛度越大，模態頻率越小[3]。在模型質量與實際零件質量一致的前提下，模型剛度偏大的可能原因如下:邊界約束方式剛度偏大；單元剛度偏大，包括連接單元和實體單元；材料剛度偏大。

邊界約束方式:后視鏡采用3個螺栓螺接在工裝上，目前采用RBE2單元模擬螺栓連接，并約束安裝點所有自由度。本文排除該約束方式對后視鏡整體模態的影響。

單元類型:模型中銷軸內部的彈簧單元在原始分析中簡化為剛性連接，為研究其影響，改為彈簧單元，賦予實際剛度。如圖7所示，改動后后視鏡第1階模態頻率值下降2.3 Hz。原始分析中，實體采用四面體1階單元模擬。四面體1階單元只有4個積分點，單元剛度偏大，但計算時間短，效率較高。四面體2階單元有10個積分點，能更好的模擬實際結構，但自由度增多，計算效率明顯下降。從圖7還可以看出，采用2階單元后，第1階模態頻率值下降10.2 Hz，由此可見，該單元積分類型影響很大。經過上述兩點修改，第1階模態頻率下降至69.1 Hz。

材料屬性:后視鏡中的基板材料為尼龍66含50%玻璃纖維（PA66+GF50），屬于各項異性材料。各項異性材料的特性是力-位移曲線與加載方向密切相關，加載力方向沿玻璃纖維長度方向時，剛度較高，加載力方向垂直于玻璃纖維長度方向時，剛度較低，如圖8所示。為了簡化各項異性材料屬性的建模，根據經驗，采用各項同性的材料建模方式來模擬各項異性材料，因此其彈性模量需要調整。目前得到的PA66+ GF50的彈性模量為12 000 MPa，圖9中為各種不同彈性模量對應的模態頻率值。根據圖9可知，PA66+ GF50彈性模量縮減30%與試驗結果一致。

根據以上對系統模態頻率影響因子的研究，調整了單元類型和各項異性材料的彈性模量，最終分析模態第1階頻率值與試驗值一致。對前3階模態頻率進一步對比如表3所示。

表3 調整后模態仿真與試驗對比

由表3可知，調整后模型前3階頻率值與試驗值的差異滿足要求，該模型可以用于后視鏡頻率響應分析。

3.4 后視鏡頻率響應分析

在后視鏡與車身連接處約束全部自由度，在連接處施加0.5 g振動激勵，振動頻率范圍為20～250 Hz。采用頻率響應分析對臺架振動光學穩定性試驗進行模擬。頻率響應分析方法有直接頻率響應與模態頻率響應2種方法，其中，模態頻率響應利用結構的模態振型來對耦合的運動方程進行縮減和解耦，求解效率高。本文由于模型計算量較大，采用高效的模態頻率響應方法。模態阻尼系數g設定直接影響系統振幅，圖10為不同模態阻尼系數下后視鏡鏡面中心振動響應幅值曲線。

根據圖10可取得不同阻尼下的共振峰值，根據公式（1）～公式（3），后視鏡固定點到測量點距離L1=216 mm，計算出不同阻尼下的后視鏡振動旋轉角和目標靶上振動位移如表4所列。由表4可得，模態阻尼系數設定為0.04時，分析結果與試驗結果最接近。因此，本文認為針對后視鏡系統，模態阻尼系數設定為0.04時比較合理，可以在此模型基礎上進行優化分析。

表4 不同阻尼下的頻響分析結果

4 后視鏡結構優化及驗證

4.1 后視鏡優化方案

首先通過查看應力云圖來尋找設計薄弱區。原設計的后視鏡基座和基板在共振情況下應力云圖如圖11所示。加強應力集中位置的剛度有利于提高共振頻率，進而減小測量點的共振位移。

根據分析結果可知，應力集中處于部分加強筋根部。綜合考慮修模成本和時間，最終確定的改進方案一是增強已有加強筋高度和厚度，二是在可以加強的位置增加加強筋，具體方案見圖12和圖13。

4.2 后視鏡優化方案驗證

表5為優化前、后的CAE仿真結果對比。根據該優化方案，對后視鏡進行了樣件試驗，表6給出了優化方案CAE仿真分析結果與試驗結果之間的差異。從表5和表6可見，CAE分析的準確度很高，改進方案效果很好。

表5 優化前、后CAE仿真分析結果對比

表6 CAE仿真分析結果與試驗結果對比

5 結束語

采用頻率響應分析方法有效解決了某項目中后視鏡光學振動穩定性失效問題。介紹了光學振動試驗原理，通過CAE方法再現了該試驗。通過試驗和仿真結果對比可知，采用頻率響應分析得出的共振頻率與位移響應差異較小，能較準確的再現問題。此外，該分析流程應用在后視鏡開發項目中，可以在設計前期掌控后視鏡光學穩定性這一重要性能，避免設計后期進行模具修改。

1唐乾.后視鏡的使用學問.汽車運用，2007，5:7～8.

2蘭靛靛.基于實驗模態分析的后視鏡結構動態修改.噪聲與振動控制.2008，10:120～121.

3傅志方，華宏星.模態分析理論與應用.上海:上海交通大學出版社，2000.

（責任編輯簾青）

修改稿收到日期為2014年11月1日。

Optical vibration Stability Optimization of Rearview Mirror Base on the Frequency Response Method

Zhao Tingting，Wang Xia，Wang Changfu
（Pan Asia Technical Automotive Center Co.，Ltd）

In order to find the cause of optical stability failure of rearview mirror of a vehicle in the validation test，we use frequency response-based CAE method to simulate the optical stability test and establish the analysis process of the frequency response.It is known from comparison between test and simulation results that the resonance frequency obtained from frequency response analysis differs slightly from displacement response，which accurately reproduces the failure，from which we put forward a corresponding solution.Finally，we use test to verify the accuracy of the analysis method and the effectiveness of the solution.

Rearview mirror，Vibration frequency response，Optical stability

后視鏡振動頻率響應光學穩定性

U463.85+6

A

1000-3703（2014）12-0009-04