對磁場中逆向思維的探討

周孝明

（江蘇省懷仁中學 江蘇 無錫 214196）

通電導線在磁場中受力運動和帶電粒子在勻強磁場中的勻速圓周運動問題可以很好地考察學生物理過程分析、空間想象和應用數學知識解決物理問題的能力，因此一直受到高考命題專家的青睞，成為歷年的熱門考題.特別是幾種邊界磁場的極值問題，如何根據題設條件確定粒子運動的臨界條件，準確確定粒子在臨界情況下的運動軌跡是解決極值問題的關鍵.對于通電導線在磁場中的運動和帶電粒子在有界勻強磁場中的勻速圓周運動，嘗試用逆向思維的方式加以分析處理并與常規方法加以比較，探究總結處理此類問題的最有效方法.

1 通電導線在磁場中的受力運動

1.1 通電直導線在磁場中的受力運動

【例1】如圖1（a）所示，把一通電直導線放在蹄形磁鐵磁極的正上方，導線可以自由移動.當導線中通過如圖所示方向的電流I時，試判斷導線的運動情況.

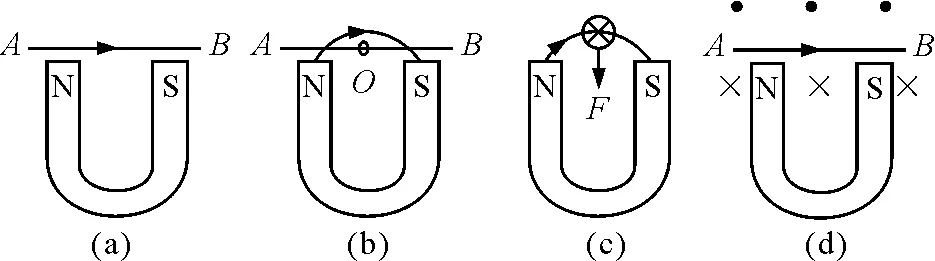
圖1

常規解法：

（1）根據圖1（b）所示的導線所處的特殊位置判斷其運動情況.將導線AB從N，S極的中間O分成兩段，由左手定則可得AO段所受安培力的方向垂直于紙面向外，BO段所受安培力的方向垂直于紙面向里，可見從上向下看，導線AB將繞O點逆時針轉動.

（2）根據導線轉過90°時的特殊位置判斷其上下運動情況.如圖1（c）所示，導線AB此時所受安培力方向豎直向下，導線將向下運動.

（3）由上述兩個特殊位置的判斷可知，當導線不在上述的特殊位置時，所受安培力使AB逆時針轉動的同時還要向下運動.

逆向思維法：

根據圖1（d）所示的導線所處的特殊位置判斷其運動情況.將通電直導線固定，判斷蹄形磁鐵的轉動.由右手螺旋定則判斷出磁鐵所在平面的磁場方向，磁鐵N極所受磁場力垂直紙面向里，S極所受磁場力垂直于紙面向外，可見從上向下看，磁鐵相對于導線將順時針轉動.則當磁鐵固定時，導線將繞O點逆時針轉動.余下求解同上.

1.2 環形導線在磁場中的受力運動

【例2】如圖2所示，把輕質導線圈用絕緣細線懸掛在磁鐵N極附近，磁鐵的軸線穿過線圈的圓心，且垂直于線圈平面，當線圈中通入如圖方向的電流后，判斷線圈如何運動？

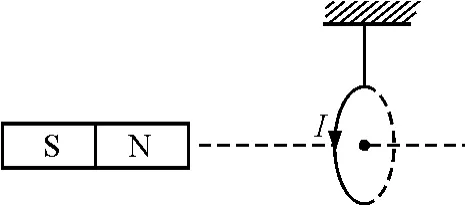
圖2

常規解法：

方法一：微元法.

首先將圓形線圈分成很多小段，每小段可看作一直線電流，取其中上、下兩小段分析，其截面圖和受安培力情況如圖3（a）所示.根據對稱性可知，線圈所受安培力的合力水平向左，故線圈向左運動.

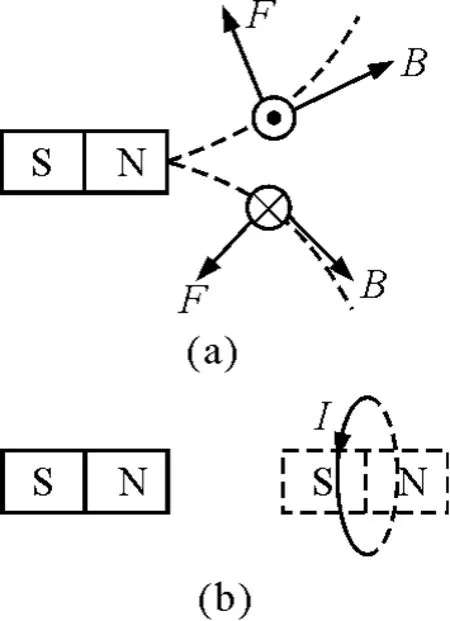
圖3

方法二：等效法.

將環形電流等效成一條形磁鐵，如圖3（b）所示，據異名磁極相吸可知，線圈將向左運動.同時，也可將左側條形磁鐵等效成一環形電流，根據結論“同向電流相吸引，異向電流相排斥”，又可得到相同的答案.

逆向思維法：

根據線圈中的電流方向結合右手螺旋定則知，通過線圈軸線的磁場方向由左端指向右端且離導線越遠磁感應強度越小，因此條形磁鐵N極受到水平向右的磁場力大于S極受到水平向左的磁場力，合力水平向右.根據力作用的相互性，線圈受到的磁場力水平向左，故線圈向左運動.

綜合以上比較可知，微元法適用的范圍較廣但學生要掌握難度較大，需要較強的綜合能力；等效法只適用環形電流與磁鐵間的相互作用有局限性.逆向思維法可以明顯降低難度，學生更易掌握.

2 帶點粒子在有界磁場中的受力運動

2.1 已知有界磁場

【例3】如圖4所示，一足夠長的矩形區域abcd內充滿方向垂直紙面向外的、磁感應強度為B的勻強磁場，在ab邊中點方向垂直磁場射入一速度方向跟ab邊夾角30°，大小為v的帶正電粒子，已知粒子質量為m，電荷量為q，ad邊足夠長，ab邊長為L，粒子的重力不計.求：粒子能從bc邊上射出磁場的v大小范圍.

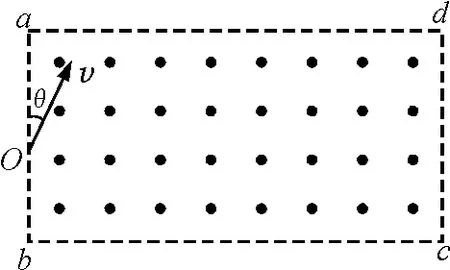
圖4

常規法（動態圓法）：

帶電粒子進入磁場時速度的方向確定，故帶電粒子在磁場中做圓周運動的軌跡圓的圓心一定在入射點O所受洛倫茲力的射線上.隨著速度的逐漸增大，整個運動軌跡圓的半徑也逐漸增大，相當于把軌跡圓逐漸放大，如圖5所示，在軌跡圓縮放的過程中就可以找到解決問題的“臨界”.經分析可得，與bc邊相切的軌跡圓的半徑是粒子能從bc邊射出磁場時的最小半徑，與ad邊相切的軌跡圓的半徑是粒子能從bc邊射出磁場區域的最大半徑.

圖5

設最小半徑為r1，最大半徑為r2，根據圖5中的幾何關系，可得

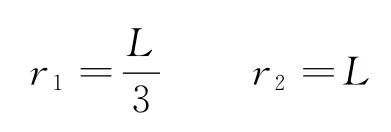
故粒子從ab邊射出的條件為

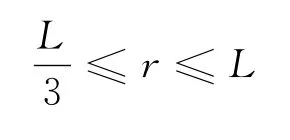
根據洛倫茲力提供向心力由公式

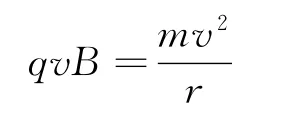
可得結果

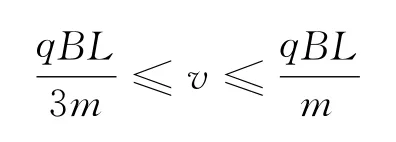
逆向思維法（動態線）：

帶電粒子進入磁場時速度的方向確定，故帶電粒子在磁場中做圓周運動的軌跡圓的圓心一定在入射點O所受洛倫茲力的射線上.在洛倫茲力的射線上任意取一個點做為圓心，畫出圓，如圖6所示.

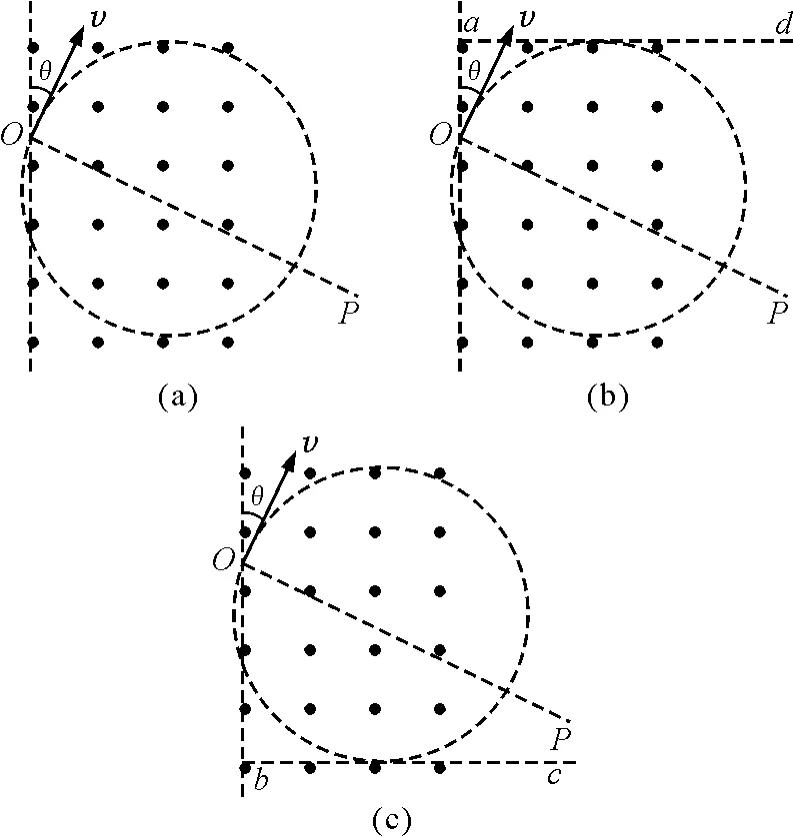
圖6

粒子要從bc邊射出，首先不能穿出ad邊，故平移ad邊至于圓相切，根據幾何關系得最大半徑r2＝L，其次恰好能從bc邊傳出，平移bc邊至與圓相切，根據幾何關系得最小半徑故粒子從bc邊射出的條件為，根據洛倫茲力提供向心力有公式可得結果

2.2 未知有界磁場

【例4】一勻強磁場，磁場方向垂直于xy平面，在xy平面上，磁場分布在以O為中心的一個圓形區域內.一個質量為m，電荷量為q的帶電粒子，由原點O開始運動，初速為v，方向沿x正方向.后來，粒子經過y軸上的P點，此時速度方向與y軸的夾角為30°，P到O的距離為L，如圖7所示.不計重力的影響.求磁場的磁感強度B的大小和xy平面上磁場區域的半徑R.

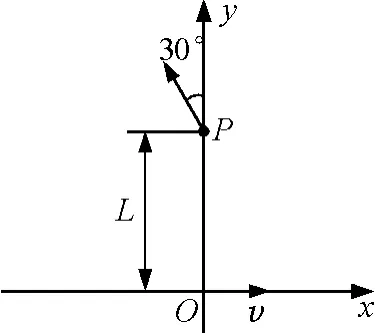
圖7

常規法（動態圓）：

帶電粒子進入磁場時速度的方向確定，故帶電粒子在磁場中做圓周運動的軌跡圓的圓心一定在y軸上，同時帶電粒子出磁場時一定沿著與y軸正方向成30°的方向，延長速度方向得PA直線.隨著速度的逐漸增大，整個運動軌跡圓的半徑也逐漸增大，相當于把軌跡圓逐漸放大，如圖8所示，在軌跡圓放大的過程中就可以找到解決問題的臨界圓.根據圖8中的幾何關系，可得根據洛倫茲力提供向心力有可得結果.根據圖可得

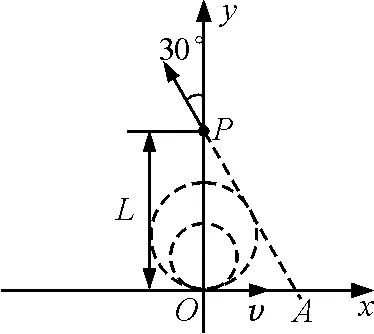
圖8

逆向思維法（動態線）：

帶電粒子進入磁場時速度的方向確定，故帶電粒子在磁場中做圓周運動的軌跡圓的圓心一定在y軸上.在y軸上任意取一點做為圓心，畫出圓，如圖9（a）所示.因帶電粒子出磁場時一定沿著與y軸正方向成30°角的方向，故平移與y軸正方向成30°的一條直線，直至與所畫圓相切.標出P點位置，OP長度.余下求解同上.

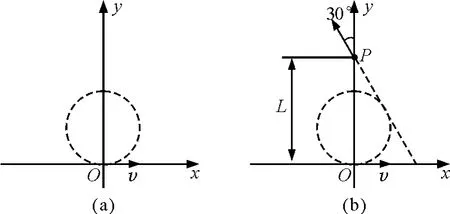
圖9

帶電粒子在磁場中做勻速圓周運動最大的難點是根據題意能畫出軌跡圓，尤其是臨界點的圓.動態圓是最常用的方法，但是對于學生的能力要求也較高，很多學生無法掌握；而動態線法顯然優于動態圓法，學生較易掌握.物理教學追求的是將復雜的問題簡單化，使之更適合學生認知的就近發展區，讓更多的學生能得到發展.