基于制造商資金約束的供應鏈博弈研究
王傳濤,紀 超,陳寶江
(北京建筑大學 機電與車輛工程學院,北京 100044)
0 引言
供應鏈是由直接或間接滿足顧客需求的各企業組成的網絡,供應鏈是動態的,它總是伴隨著物流、信息流和資金流的持續流動,供應鏈管理實際上就是對這“三流”的協調管理,在過去的供應鏈管理研究文獻中,大都集中在供應鏈中的信息流與物流的管理。對供應鏈資金流的管理,是近幾年才出現的一個研究方向,盡管研究時間較短,但供應鏈資金流的管理已成為現在學術界和實業界共同關注的熱點問題。
陳祥鋒和朱道立對資金約束供應鏈中物流提供商的價值進行了研究,主要分析了三種結構(傳統結構、代理結構與控制結構)下,供應鏈中企業的金融與運營博弈問題[1]。陳祥鋒、朱道立和應雯珺對資金約束與供應鏈中的融資和運營綜合決策問題進行了研究,主要分析了零售商存在資金約束時,供應鏈通過融資服務來緩解資金不足時的供應鏈博弈問題[2]。周建亨研究了零售商存在資金約束的供應鏈中,同時存在融資和回購的供應鏈決策問題[3]。袁牧和萬國華研究了零售商在面臨資金約束的條件下,零售商的最優訂貨策略和營銷策略[4]。剛號、唐小我和慕銀平考慮了損失厭惡的零售商在資金約束的情形下通過考慮延遲支付來分析供應鏈的運作與協調問題,他們研究發現通過引入回購合同可以使供應鏈達到協調,同時回購合同在一定程度上可以緩解零售商資金不足的狀況[5]。張義剛和唐小我則對零售商資金約束下的制造商最優策略問題進行了研究[6]。綜合現有的文獻,基本上都是對基于零售商資金約束的供應鏈博弈和協調管理問題的研究,很少探討制造商面臨資金約束下的供應鏈決策管理問題。本文將對制造商面臨資金約束下的供應鏈博弈問題進行研究。
1 基本模型
考慮由一個制造商與一個零售商組成的二級供應鏈,假設制造商能準確預測市場需求,并根據市場需求生產產品,然后將產品銷售給零售商,零售商根據制造商提供的批發價,選擇向制造商購買一定數量的產品,制造商將零售商訂購的產品送到零售商處,零售商將相關的款項支付給制造商,最后零售商將產品銷售給消費者。我們假設供應鏈中的所有信息都是對稱的,即供應鏈中的所有信息在制造商和零售商都是共享的,假定制造商和零售商都是風險中性的,并且都是追求利益最大化的決策者。該決策模型可以看作一個Stackelberg博弈,其中制造商是決策中的領導者,零售商是決策中的跟隨者。
假定制造商的單位生產成本為c,產品的市場需求是d=D-kp,其中D代表市場的最大需求量,P代表零售商的零售價格,0>k是價格敏感系數,d代表市場的需求。并且p>c總是成立的。c,D,k是外生的,為常數。
假設制造商提供給零售商的單位產品批發價用w表示,則制造商、零售商、供應鏈的利潤分別為:fm=(w-c)Q ,fr=( p-w)Q和fsc=( p-c) Q。由于制造商和零售商是一個Stackelberg博弈,經過簡單計算可知,制造商和零售商博弈的結果是,制造商確定的單位產品批發價商向制造商的采購數量位產品零售價
2 制造商資金約束下的供應鏈博弈
在上節中,我們討論了無資金約束下供應鏈的博弈情況,但在實際的生產運營中,制造商經常會遇見資金短缺的情況,這時,制造商在產品生產的過程中就會面臨生產中斷或是無法滿足零售商訂貨的損失。本節將探討制造商在面臨資金約束下的供應鏈的博弈問題。
2.1 制造商資金不足時供應鏈的博弈
假設制造商的自有資金為A,通過第二節的討論我們知道,當A<,即制造商的自有資金不能生產出滿足零售商需求數量的產品,即當造商憑自有資金A,無法生產出滿足零售商需求的數商在生產產品時不會有資金不足的情況發生。因們來看制造商和零售商的博弈。本小節我們還假定制造商資金不足時,不采取其它措施來增加資金。
制造商的決策問題為:

由于信息是對稱的,所以零售商也知道制造商的資金不足,所以零售商的決策問題為:
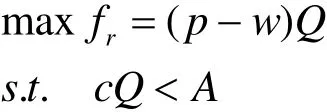
在不考慮資金約束的情況下, fm在約束時,有>A,所以當制造商在設置批發價為w,零售商會訂購Q數量的產品,但由于制造商的資金限制無法生產出Q數量的產品,也就無法滿足零售商的需求,零售商訂貨時就不會訂購Q數量的產品,這時制造商就會根據零售商的決策重新制定批發價。顯然 fm是關于w的凹函數,當所以,我們有下面的定理1:
通過定理1,我們知道,制造商的批發價格和零售商的零售價都隨著制造商自有資金A的增大而降低,零售商的訂貨量隨著制造商自有資金A的增大而增大。主要原因在于當制造商的自有資金增大時,制造商為了賺取更多的利潤,它會降低產品的批發價來刺激零售商訂更多數量的產品;而對零售商來說,當制造商降低批發價后,它為了獲得更多的利潤,肯定會訂購更多數量的產品,同時,為了銷售更多數量的產品,它也會相應的降低產品的零售價格來吸引消費者。實際上,對于零售商而言,單位產品的凈收益為制造商的自有資金增大時,零售商單位產品凈收益會隨之增大,因此,零售商只要訂購的產品能銷售出去,總會訂購更多數量的產品來獲取更多利潤。
2.2 制造商資金不足但能提前收款時供應鏈的博弈
假定制造商為了鼓勵零售商提前付款,會給零售商一定的折扣,設折扣率為a(0≤a≤1),假定零售商的提前付款資金會產生機會成本,即零售商若不提前付款,可以把這部分資金投入其它的投資活動來賺取利潤,假定資金的機會成本率為g( g ≥ 0 ),g也可以理解為資本市場的平均投資回報率。不是一般性,假定g<a,即資金的機會成本率總小于制造商的折扣率,否則零售商就不會提前付款。同樣的制造商提前收到零售商的款項后,剩余的資金也會產生相應的收益,收益率為g。
這時,制造商的利潤函數為:

零售商的利潤為:

我們有下面的定理2:
定理2 當制造商資金不足,且制造商能要求零售商提前付款時,制造商和零售商博弈后,制造商的批發價為:

零售商的訂貨量為:

產品的零售價為:

證明:由于制造商和零售商的博弈仍然是Stackelberg博弈,所以先對 fr求導并令其為0,可得:
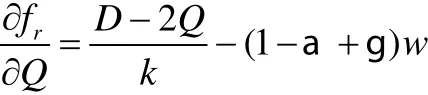

當w給定時,(6)式是(2)式的最優解。
將(6)式代入(1),同理可知 fm是關于w的凹函數,對 fm關于w求一階導數,并令其為證。
根據定理2,可以得下面的推論:
推論:1) 制造商的批發價隨著產品折扣率的上升而上升,隨著資金機會成本的上升而降低;2)零售商的訂貨量隨著產品折扣率和資金機會成本的上升而降低;3) 零售商的產品零售價隨著產品折扣率的上升而降低,隨著資金機會成本的上升而降低;4) 制造商和零售商的利潤同時隨著產品折扣率和資金機會成本的上升而降低。
特別的,當 g = 0 時,即資金的機會成本為零(這在企業的實際生產中也是存在的,比如當產品的銷售周期很短時,制造商和零售商的資金在該期間的機會成本就可以忽略不計)。根據定理2,可知此時制造商的產品批發價售商的產品零售應商和零售商的利潤分別為供應鏈沒有資金約束時的博弈結果相比,零售商的訂貨量和產品零售價是完全相等的,供應商和零售商的利潤也完全相等。由于0≤a≤1,所以批發價比原來時要高。這就意味著,當資金的機會成本不存在時,若制造商可以要求零售商提前付款并提供折扣,制造商可以通過提高目標批發價,但打完折扣之后的批發價與沒有資金約束時的相等,這樣零售商就會訂購與沒有資金約束時一樣的產品數量,制定與沒有資金約束時相同的產品零售商,從而獲得與沒有資金約束時相同的利潤。因此,當資金的機會成本為零時,制造商可以通過要求提前支付并給予折扣的方式完全消除資金短缺的影響。
3 結論
資金約束在供應鏈的決策中是一種很常見的情況,現有文獻大都考慮零售商的資金不足時供應鏈的博弈問題,本文則對制造型供應鏈中制造商生產產品時自有資金不足時供應鏈的博弈問題進行了研究。分別探討了制造商在面臨資金約束時不通過相關措施解決資金問題與通過要求零售商提前支付來解決自有資金的不足,當制造商不采取措施時,研究發現,資金約束會給供應鏈的博弈帶來影響,制造商和零售商的利潤隨著制造商自有資金的增多而增大。當制造商通過要求零售商提前支付訂貨款并給予零售商一定的折扣時,研究發現制造商和零售商的利潤同時隨著產品折扣率和資金機會成本的上升而降低。但當資金機會成本為零時,制造商能通過要求零售商提前付款并給予折扣的方式完全消除資金短缺的影響。
[1] 陳祥鋒,朱道立.資金約束供應鏈中物流提供商的系統價值研究[J].系統工程學報,2008,23(6):666-673.
[2] 陳祥鋒,朱道立,應雯珺.資金約束與供應鏈中的融資和運營綜合決策研究[J].管理科學學報,2008,11(3):70-78.
[3] 周建亨.供應鏈中融資與回購決策分析[J].工業工程,2010,13(3):25-28.
[4] 袁牧,萬國華.資金約束零售商的訂購與營銷聯合決策研究[J].西南民族學院學報(自然科學版),2013,39(5):806-812.
[5] 剛號,唐小我,慕銀平.延遲支付下損失厭惡型零售商參與的供應鏈運作及協調[J].控制與決策,2013,28(7):1023-1027.
[6] 張義剛,唐小我.供應鏈融資中的制造商最優策略[J].系統工程理論與實踐,2013,33(6):1434-1440.

