廣義代數幾何碼探究
王 貞
(池州學院 數學與計算機科學系,安徽 池州247000)
廣義代數幾何碼探究
王 貞
(池州學院 數學與計算機科學系,安徽 池州247000)
廣義代數幾何碼是通過有限域上的代數函數域中一些次數較低的位而得到的一種碼。在此基礎上,通過構造函數域碼和廣義代數幾何碼的子域子碼,從而得到參數更好的線性碼。
位;代數幾何碼;函數域碼;子域子碼
1 引言
20世紀70年代,Goppa[1]首先利用有限域上的代數曲線來構造碼。20世紀80年代初,Tsfasman[2]等人將Goppa思想與代數幾何相結合,構造出一系列糾錯碼,使其信息率超過Gilbert-Varshamov界。代數幾何碼主要利用有限域上代數曲線的有理點構造線性碼。對于有限域,當較小時,建立在其上的代數曲線的有理點很難構造出好的代數幾何碼。由于這樣的局限性,人們嘗試用次數高于1的位去構造線性碼,并取得了好的漸近系數[3-4]。
Xing[5]通過高次數級聯碼構造廣義代數幾何碼,將代數幾何碼進行推廣,并且得到非常好的線性碼。本文在此基礎上,通過構造其子域子碼,得到參數更好的線性碼。
2 預備知識
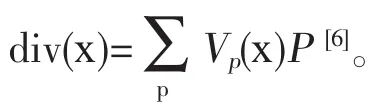
對于任意一個Fr(x)中除子G,向量空間

是一個有限維線性空間,由Riemann-Roch定理[6],
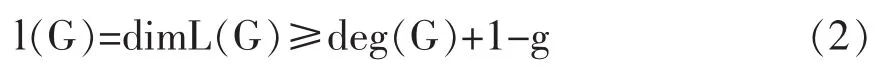
其中g為x的虧格。當deg(G)≥2g-1時,(2)式取等號。
令P1,P2, …,Ps為x上s個互不相同的位,deg(Pi)=ki,1≤i≤s,且滿足supp(G)∩{P1,P2,…,Ps}=.
定義1[7]函數域碼是Fr(x)一個非零有限維的Fr線性子空間V滿足:
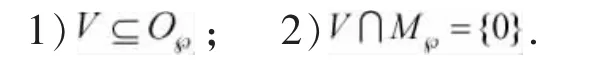
Ci表示r元線性碼[ni,ki=deg(Pi),di],1≤i≤s。 πi表示Fr上Frki到Ci的單同態。令

定義2[5]上述映射α的象稱為廣義代數幾何碼,記為C(P1,P2,…Ps;G;C1,…Cs).
當Pi為有理位時,有ni=ki=di=1,1≤i≤s,C(P1,P2,…Ps;G;C1,…Cs)為Goppa代數幾何碼。
3 主要結論


令C是Fr上線性碼[N0,K0,D0],為Fq上線性碼[N0,K0,D0],C|Fq稱為C的子域子碼,k0≥sK0-(s-1)N0,d0≥D[8]。 從而得到:
定理3 設C(P1,P2,…Ps;G;C1,…Cs)為來自函數域碼V(G)的廣義代數幾何碼[N,K,D],C(P1,P2,…Ps;G;C1,…Cs)|Fq為其子域子碼[N,K,d],則,k≥sK-(s-1)N,d≥D.
通過有限域Fr上函數域碼V(G)來構造廣義幾何碼C(P1,P2,…Ps;G;C1,…Cs),該廣義幾何碼具有非常的參數。在此基礎上,進一步構造廣義幾何碼的子域子碼,由定理3可以看出,其子域子碼有更好的參數。
[1]V D Goppa,Codes associated with divisors[J].Probl.Inform.Transm.1977,13:22-26.
[2]M A Tsfasman.S.G.Vlǎdut,and T.Zink.Modular curves,Shimura curves and Goppa codes,better than Varshamov-Gilbert bound.Math[J].Nachriechten,1982,109:21-28.
[3]H Niederreiter,C P Xing,and K Y Lam,A new construction of algebraic-geometry codes[J].Applicable Algebra Engineering.Comm.Comput,1999(9)373-381.
[4]Wanbao Hu,Zhen Wang,Improvements on the distance of onepoint codes using places of higher degree[J].Procedia Engineering,2011(15):1711-1715.
[5]Chaoping Xing,Harald Niederriter,and Kwok Yan Lam,A Generalization of Algebraic Geometry Codes[J].IEEE transations on information theory,1999(7):1123-1127.
[6]H.Stichtenoth.Algebraic Function Fields and Codes[M].Berlin:Springer-Verlag,1993.
[7]Hachenberger D,Niederreiter H,Chaoping Xing Functionfield codes[J].Applicable Algebra in Engineering,Communication and Computing,2008,19(3):201-211.
[8]Chaoping Xing,San Ling,A class linear codes good parameters from algebraic curves[J].IEEE Inform Theory,2000,46(4):1527-1532.
[責任編輯:桂傳友]
O175
A
1674-1102(2014)06-0039-02
10.13420/j.cnki.jczu.2014.06.010
2014-07-23
池州學院研究生引進啟動項目(2011RC035)。
王貞(1987-),男,安徽東至人,池州學院數學與計算機科學系助教,碩士,研究方向為代數編碼。

