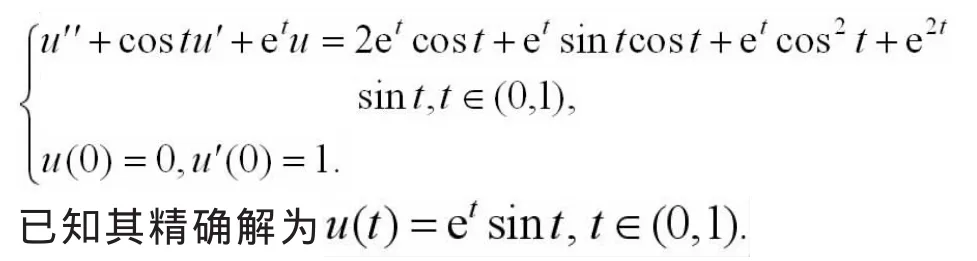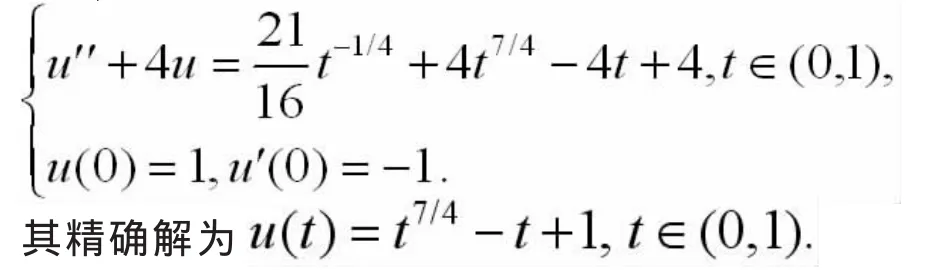時間C0-連續一次有限元法的先驗誤差分析
賴軍將
(閩江學院 數學系,福建 福州350108)
時間C0-連續一次有限元法的先驗誤差分析
賴軍將
(閩江學院 數學系,福建 福州350108)
對于變系數二階常微分方程的初值問題,應用時間C0-連續一次有限元方法數值求解。在對網格剖分的適當限制下,獲得了數值方法的穩定性結果。賦以有限元空間相應的范數,證明了在該范數意義下方法的先驗誤差估計。數值實驗結果驗證了該方法的收斂率。
連續一次有限元;誤差分析;穩定性;收斂性
引言
時間連續有限元方法是數值求解微分方程的一種有效算法[1-3].對于二階常微分方程初值問題,文獻[4]給出了相應的時間C0-連續有限元法計算格式,并且得到了時間C0-連續m(m≥2)次有限元方法的先驗誤差估計.文獻[5]對于一類二階常系數齊次線性常微分方程,采用直接計算的方法獲得了時間C0-連續一次有限元法的先驗誤差估計.文獻[3]采用時間連續有限元法數值求解二階發展問題,進行了后驗誤差分析并提出了一個自適應算法.
本文對于一般情形的變系數二階常微分方程的初值問題,在文獻[5-7]的基礎上,利用回收技巧[1]和離散Gronwall引理[8],獲得了時間C0-連續一次有限元法對初值的穩定性.并且對有限元空間賦以相應的范數,證明了在此范數意義下的先驗誤差估計結果.
本文使用Sobolev空間的標準符號[9].對于ν(t)∈H2(0,T),定義
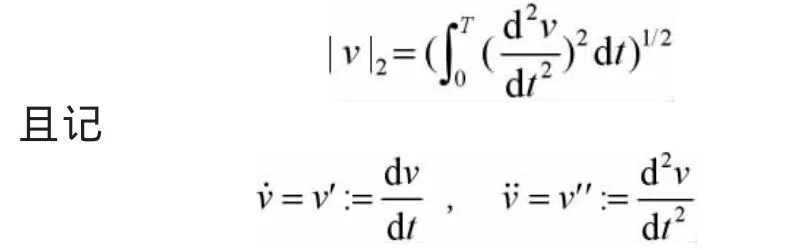
將“≤C…”簡記為“^…”,其中正常數C在不同地方可取不同的值,它與方程右端項,真解函數以及網格剖分尺寸無關.
1 求解格式與相容性
討論二階常微分方程的初值問題[7]:
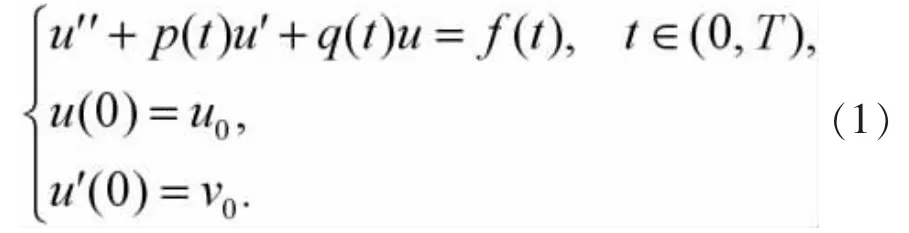
初值u0與ν0事先給定,已知函數p,q,f適當光滑,并設
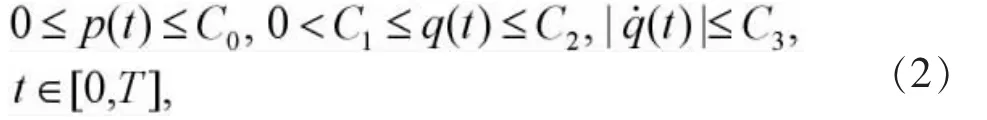
其中C0,C1,C2,及C3都為正常數.
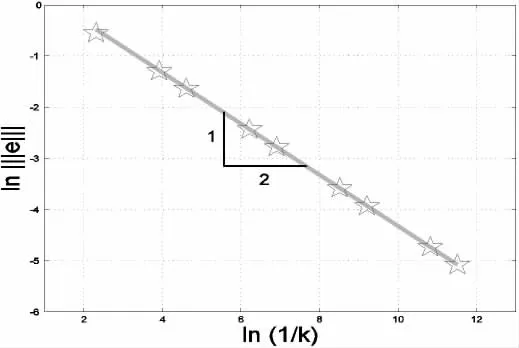
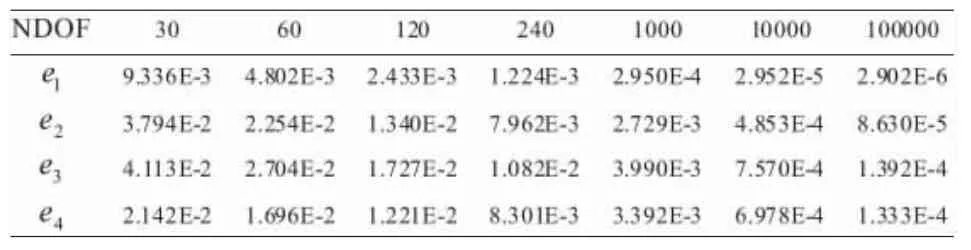
對求解區間I=(0,T)進行擬一致剖分:t0=0 這里,空間P1(In)由In上所有次數不超過1的多項式組成.于是數值求解問題(1)的時間C0-連續一次有限元法為[4-5]:求U(t)∈Sk使得從這里開始,分別用u和U表示方程(1)及(3)的解,并假設有正則性u∈H2(I).于是下式恒成立, 在式(3)中,對n從1到N求和得到 從而由式(4)-(5)可知 即時間C0-連續一次有限元法具有相容性. 賦以有限元空間Sk以下范數, 引理1對w∈Sk以下等式成立, 綜合式(6)和式(9)-(11)得證引理. 引理2對w∈Sk以下不等式成立, 證明 由于w∈Sk,在任一區間In上w可線性表示成 由直接積分,且應用算術幾何平均值不等式可獲得證明. 利用引理1,(5)式和式(7),若f(t)=0,則有 由T的任意性,得到了下述穩定性定理. 定理1 設U∈Sk為方程(3)的解,f=0且條件(2)滿足.則當k 記u在Sk中的分段線性插值函數為πu,即有 考慮二階常微分方程初值問題 采用時間C0-連續一次有限元法求解以上問題并取均勻剖分計算.表1列出了取不同步長時的誤差,表明都小于某一有界常數,而且在||·||||意義下此方法具有階的收斂速度[11]. 表1 取不同步長的誤差 由表1中的誤差結果,可獲得圖1所示的雙對數誤差圖,從圖1可知,經取對數后的誤差結果落在斜率為-的一條線段上,即驗證了在意義下此方法收斂階為階,與定理2的結論相吻合. 圖1 取不同步長的雙對數誤差 以下采用時間C0-連續一次有限元法(18)(簡稱CG1)及幾類典型的時間離散化格式[12]求解初值問題 分別采用CG1方法,三層格式 (θ=0)[12],兩層格式(θ1=1,θ2=1/2)[12]及兩層格式(θ1=θ2=1)[12]進行數值計算,記以上方法在T=1處數值解的誤差絕對值分別為e1,e2,e3和e4, 自由度數 (未知量數)為NDOF,表2給出了不同方法的誤差結果,表明在自由度數相同的情況下求解以上問題,CG1方法獲得的數值解在時間節點處較其它方法準確.圖2給出了相同自由度數時由不同方法獲得的解曲線,從此圖可知,用CG1方法求解以上問題獲得的數值解較其它方法更逼近精確解. 表2 不同方法的節點誤差 圖2 不同方法獲得的解曲線,NDOF=60 [1]Thomée V.Galerkin finite element methods for parabolic problems[M].2nd.ed.Berlin:Springer-Verlag,2006. [2]Lai J, Huang J, Chen C. Vibration analysis of plane elasticity problems by the continuous time stepping finite element method[J].Applied Numerical Mathematics,2009,59(5):905-919. [3]Huang J,Lai J,Tang T.An adaptive time stepping method with efficient error control for second-order evolution problems[J].Science China Mathematics,2013,56:2753-2771. [4]陳傳淼,謝資清.非線性微分方程多解計算的搜索延拓法[M].北京:科學出版社,2005. [5]賴軍將,王強,黃建國.二階雙曲型方程的CO-連續一次有限元法[J].上海交通大學學報,2008,42:2065-2069. [6]HulbertG.Time finite elementmethodsforstructural dynamics [J].InternationalJournalforNumericalMethods in Engineering,1992,33:307-331. [7]賴軍將.二階常微初值的時間間斷最小二乘有限元法[J].應用數學與計算數學學報,2012,26:35-44. [8]Quarteroni A,Valli A.Numerical approximation of partial differential equations[M].Berlin:Springer-Verlag,1994. [9]Adams R A,Fournier J.Sobolev spaces[M].2nd.ed.New York:Academic Press,2003. [10]Brenner S C,Scott L R.The mathematical theory of finite element methods[M].3rd.ed.Berlin:Springer-Verlag,2008. [11]Adjerid S,Temimi H.A discontinuous Galerkin method for the wave equation[J].Computer Methods in Applied Mechanics and Engineering,2011,200:837-849. [12]黃明游.發展方程數值計算方法[M].北京:科學出版社,2004. [責任編輯:桂傳友] O241 A 1674-1102(2014)06-0025-04 10.13420/j.cnki.jczu.2014.06.006 2014-07-06 國家自然科學基金資助項目(11101199);福建省高等學校新世紀優秀人才支持計劃資助(JA12260)。 賴軍將(1977-),男,湖南攸縣人,閩江學院數學系副教授,博士,主要從事科學計算研究。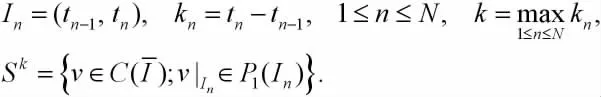
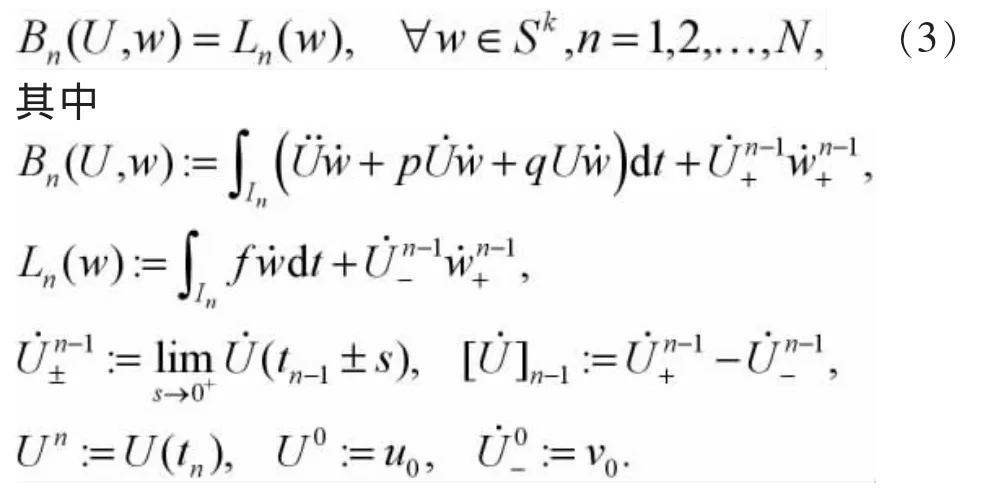

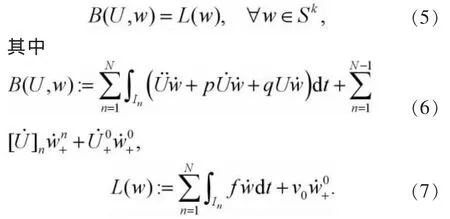

2 穩定性分析
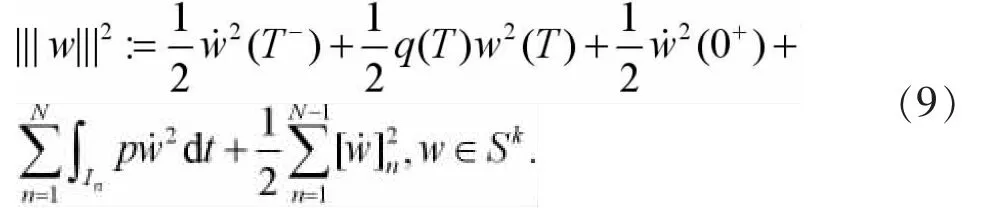

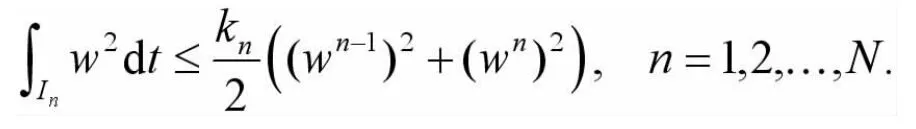
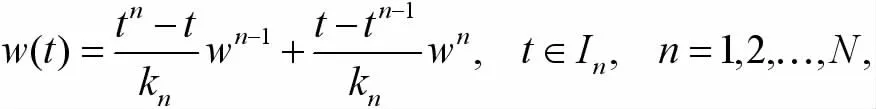

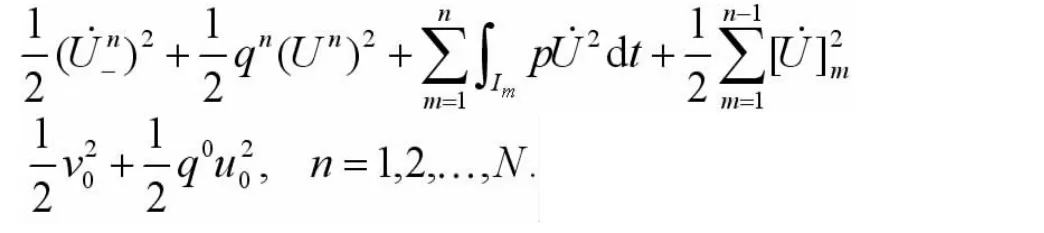
3 誤差估計
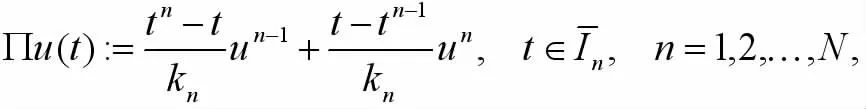


4 數值實驗