熱防護系統(tǒng)耦合分析方法與應用

桂業(yè)偉，劉磊，杜雁霞

(中國空氣動力研究與發(fā)展中心 空氣動力學國家重點實驗室，四川 綿陽 621000)

0 引言

熱防護技術(shù)是保證航天飛行器在上升/再入段受氣動加熱環(huán)境下不至發(fā)生結(jié)構(gòu)過熱甚至燒毀的一項關(guān)鍵技術(shù)，也是保證導彈在氣動加熱環(huán)境下正常工作的一項關(guān)鍵技術(shù)。隨著導彈技術(shù)的發(fā)展，特別是高超聲速巡航彈的出現(xiàn)，長時間飛行導致氣動力、熱與結(jié)構(gòu)間的多物理場耦合效應更加顯著，對導彈的熱防護系統(tǒng)進行耦合分析已勢在必行。在長時間高馬赫數(shù)飛行條件下，彈體結(jié)構(gòu)可能在氣動力載荷與結(jié)構(gòu)熱/力作用的綜合影響下產(chǎn)生結(jié)構(gòu)變形。變形又會影響氣動加熱及結(jié)構(gòu)的熱/力響應特性，這就形成了復雜的多場耦合關(guān)系，如圖1所示。開展一體化熱防護系統(tǒng)耦合分析方法研究，對深刻把握熱防護系統(tǒng)多場耦合規(guī)律及其效應，準確評估熱防護結(jié)構(gòu)安全性，提高防熱結(jié)構(gòu)設(shè)計水平，從而提高導彈性能有著極為重要的意義。

圖1 氣動力/熱與結(jié)構(gòu)間的相互影響關(guān)系Fig.1 Relationship between aerodynamic force/ thermal and structure

針對防熱結(jié)構(gòu)內(nèi)部力、熱與結(jié)構(gòu)高度耦合的現(xiàn)象，國外較早開展了熱防護一體化分析方法的研究。Thornton E. A.和Dechaumphai P.在1988年就提出了多場耦合的問題[1]，并發(fā)表了關(guān)于多場耦合分析研究方面的成果。Chen[2]將耦合計算方法應用到航天領(lǐng)域，對再入火星大氣層的探測器進行了流場和結(jié)構(gòu)傳熱的松耦合計算，并對松耦合迭代計算中迭代次數(shù)和計算精度的關(guān)系問題進行了研究。德國科學家[3]通過未來空間運載系統(tǒng)技術(shù)(technology for future space transportation systems,TETRA)和未來空間運載系統(tǒng)應用技術(shù)(selected system and technologies for future space transportation systems applications,ASTRA)的支持，較為深入地開展了氣動力/熱與結(jié)構(gòu)耦合問題研究，并采用如圖2所示的縫隙模型驗證了相關(guān)的耦合方法。

圖2 耦合試驗模型Fig.2 Coupling test model

國內(nèi)學者在20世紀90年代初曾進行過彈頭沿彈道燒蝕耦合計算方面的研究工作，以邊界層理論或者其他近似計算方法沿彈道給出冷壁條件下的氣動熱環(huán)境，經(jīng)熱壁修正后用于結(jié)構(gòu)燒蝕及熱響應計算。這類方法屬于工程方式的耦合計算，有一定的實際應用價值。20世紀90年代末至本世紀初，國內(nèi)學者[4-5]率先在國內(nèi)開展了氣動熱和熱響應的耦合研究。隨后研究人員[6-7]又針對飛行器防熱結(jié)構(gòu)，開展了氣動熱/熱響應/熱應力多場耦合一體化預測方法研究，逐步發(fā)展形成了初具雛形的熱防護綜合分析方法及軟件系統(tǒng)。本文較為系統(tǒng)的歸納了多種熱防護系統(tǒng)耦合分析策略與方法，并列舉了耦合分析方法的實際工程應用。

1 多場耦合分析思路與策略

在計算中使用合理的耦合策略與分析方案，是多場解決問題的有效途經(jīng)。本文根據(jù)氣動力/熱與結(jié)構(gòu)多物理場間的耦合關(guān)系，提出了如下4種具有較高工程實用價值的耦合策略。通過這幾種耦合分析方案的實際運用，能較好地解決目前工程中實際面臨的大部分熱防護系統(tǒng)耦合分析問題。

1.1 氣動熱與熱響應的耦合(雙向面耦合)

氣動熱與結(jié)構(gòu)熱響應之間通過飛行器表面的熱量傳遞緊密耦合在一起，屬于典型的雙向面耦合。研究表明，氣動熱與結(jié)構(gòu)熱響應之間的雙向面耦合可通過3種解耦方式實現(xiàn)：

(1) 熱壁修正法

根據(jù)沿彈道冷壁熱流，實時修正結(jié)構(gòu)熱響應計算時進入防熱結(jié)構(gòu)的熱流值。

(2) 錨點迭代法

根據(jù)當前錨點壁溫求解熱壁熱流，在通過熱壁熱流計算下一錨點的結(jié)構(gòu)壁溫。如此迭代推進。

(3) 整體耦合迭代法

沿彈道計算飛行器表面的冷壁熱環(huán)境；以熱環(huán)境為輸入條件計算沿彈道的防熱結(jié)構(gòu)熱響應情況；再根據(jù)獲得的表面溫度沿彈道變化結(jié)果，計算得到壁溫變化情況下的熱流分布情況。重復以上過程直到熱環(huán)境和熱響應計算結(jié)果收斂。

1.2 熱響應與熱應力/熱變形的耦合(雙向體耦合)

結(jié)構(gòu)溫度的非均勻上升、溫度梯度的形成會使結(jié)構(gòu)產(chǎn)生熱應力，同時還會給結(jié)構(gòu)帶來熱變形。應力/應變會對一些材料特性(接觸熱阻、導熱率等)造成一定影響，如在氣動力等共同外部因素下結(jié)構(gòu)發(fā)生大變形，則會進一步影響到熱響應規(guī)律。對于長時間加熱的新型高超聲速飛行器來說，結(jié)構(gòu)熱響應與熱應力/熱變形的耦合通常是無法忽略的。

對于結(jié)構(gòu)熱響應和熱應力/熱應變的耦合問題，計算的結(jié)構(gòu)模型一致，但結(jié)構(gòu)應力彈性波的傳播和熱量傳遞的時間特征尺度相差甚遠。在結(jié)構(gòu)發(fā)生溫度改變后，熱應力產(chǎn)生變化的時間對傳熱來說可忽略不計。因此，在計算分析時，熱響應計算得到的溫度信息與熱應力計算需要的溫度信息直接點點對接即可。變形場和溫度場也可采用同一套計算網(wǎng)格，以減少三維差值誤差。計算時間上，通過分析材料特性和溫度梯度的大小，在典型時刻點(或等間距的時刻點)計算應力/應變場信息，并將計算結(jié)果(網(wǎng)格變形量、材料變化量)反饋給熱響應計算模塊進行迭代耦合求解。

1.3 氣動力/熱與結(jié)構(gòu)的多場耦合(雙向面體耦合)

結(jié)構(gòu)變形量的大小受熱壁熱流、飛行器外形、結(jié)構(gòu)溫度與材料參數(shù)的影響，同時，飛行器氣動力/熱的變化量也直接受到結(jié)構(gòu)變形量的大小影響。結(jié)構(gòu)變形造成的飛行器外形變化對氣動力/熱特性造成變化屬于面耦合，氣動熱特性的變化對熱響應規(guī)律造成變化也屬于面耦合，熱響應規(guī)律的變化，造成結(jié)構(gòu)熱應力和熱變形屬于體耦合，因此考慮結(jié)構(gòu)形變的氣動力/熱/結(jié)構(gòu)多場耦合最為復雜。

由于涉及的物理場較多，計算量極大，耦合策略有較大難度。變形場/應力場的計算頻率、氣動力/氣動熱的更新頻率將直接影響耦合效率和計算精度。研究表明，考慮飛行彈道和計算過程中結(jié)構(gòu)內(nèi)溫度梯度的特點，計算典型狀態(tài)下(或等間距的時刻點)結(jié)構(gòu)變形場，并根據(jù)變形信息及時修正氣動力/熱信息是較好的耦合計算策略。

1.4 艙內(nèi)外耦合熱分析(雙向面體耦合)

由于高能密度儀器設(shè)備的采用，艙內(nèi)儀器設(shè)備發(fā)熱對艙段結(jié)構(gòu)傳熱的影響已不容忽視，當考慮艙內(nèi)熱環(huán)境對結(jié)構(gòu)熱響應的影響時，需建立結(jié)構(gòu)熱響應與艙內(nèi)熱環(huán)境的耦合分析方法。對于艙內(nèi)多部件復雜系統(tǒng)，通常基于集總參數(shù)法，采用熱網(wǎng)絡節(jié)點法建立相應的溫度場預測方法。結(jié)構(gòu)熱響應部分一般采用基于有限體積或有限元的數(shù)值計算方法。由于結(jié)構(gòu)傳熱與艙內(nèi)溫度場的時間尺度通常在同一量級，因此，耦合的重點在于空間物理場的數(shù)據(jù)傳遞。采用高效、高精度的數(shù)據(jù)插值方法，實現(xiàn)熱網(wǎng)絡節(jié)點與網(wǎng)格點之間的數(shù)據(jù)交互，進而實現(xiàn)結(jié)構(gòu)熱響應與艙內(nèi)熱環(huán)境耦合分析的有效途徑之一。

2 各物理場數(shù)值計算方法

2.1 氣動熱計算方法

(1) 氣動熱工程計算方法

對于有攻角飛行器氣動加熱，工程上通常采用跟蹤流線法來計算。跟蹤流線法主要思想是利用軸對稱比擬概念，在彈體上布滿流線，利用小橫向流假設(shè)沿每根流線按等價的軸對稱體處理，將三維邊界層問題簡化為流線坐標下的軸對稱問題。層流熱流用修正的Lees公式或工程方法計算，湍流熱流用經(jīng)過形狀因子和壓縮因子修正的平板湍流參考焓方法，用工程方法近似計算激波形狀。舵面迎風面熱流按鈍前緣平板計算，前緣駐點線的熱流用修正的無限后掠圓柱理論計算，干擾區(qū)的熱環(huán)境通常用試驗數(shù)據(jù)擬合關(guān)聯(lián)方法計算。

(2) 氣動熱數(shù)值計算方法

三維非定常可壓縮Navier-Stokes方程的直角坐標無量綱守恒形式可寫為

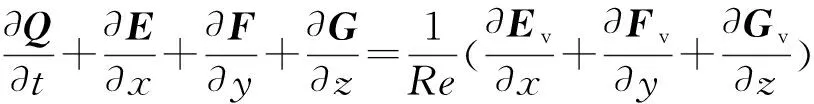
式中：Q為守恒狀態(tài)變量；E，F(xiàn)，G為無粘通量向量；Ev，F(xiàn)v，Gv為粘性通量向量；Re為方程無量綱過程產(chǎn)生的無量綱系數(shù)，即通常所稱的Reynolds數(shù)。

采用全層流計算，粘性系數(shù)由Sutherland公式給出，Prandtl數(shù)取Pr=0.72，對于空氣的比熱比計算中取常數(shù)γ=1.4。無粘通量向量采用Hanel修正的Van Leer[8-9]通量向量分裂方法計算，重構(gòu)采用帶有Van-Albada限制器的MUSCL[10-12]方法，定常計算時間上采用LU-SGS方法迭代進行。

2.2 艙內(nèi)熱環(huán)境計算方法

基于節(jié)點熱網(wǎng)絡法，艙段內(nèi)部考慮導熱、對流及輻射等過程的傳熱控制過程可描述為

2.3 熱響應計算方法

直角坐標系的結(jié)構(gòu)熱響應控制方程可表示為

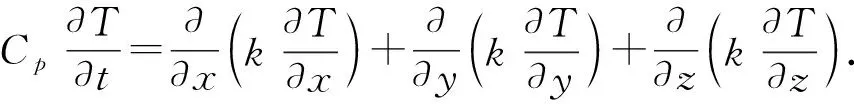
對上式在控制單元內(nèi)進行積分可以得到

式中：V為單元體積；n為單元邊界的外法向；N為單元的面總數(shù)(k=1,2,…,N)；Sk為單元k面的面積；qk為單元k面的熱流。

時間方向采用二階TVD-Runge-Kutta方法進行離散可以得到如下形式：

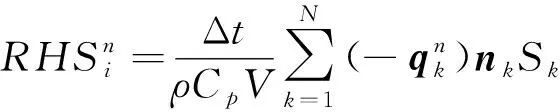
式中：i為單元序號；n為n時刻；N為單元邊界面的個數(shù)；V為單元的體積；Sk為單元邊界面的面積；nk為單元邊界面的外法向單位向量。

2.4 熱變形/熱應力計算方法

對物體受熱產(chǎn)生的應力問題，物體由于熱膨脹只產(chǎn)生線應變，而剪切應變?yōu)?。這種由于熱變形產(chǎn)生的應變可以看作初應變ε0，表達式為

ε0=α(φ-φ0).

在這種情況下應力應變關(guān)系就可表示為

σ=D(ε-ε0)，

式中：α為材料的熱膨脹系數(shù)(1/℃)，對各向異性復合材料來說，各方向的膨脹系數(shù)α通常是不相同的；φ0為結(jié)構(gòu)的初始溫度場；φ為結(jié)構(gòu)的穩(wěn)態(tài)或瞬態(tài)溫度場。φ可由溫度場分析得到的單元結(jié)點溫度φi插值求得。對求解域進行有限元離散，根據(jù)彈性力學變分原理就得到有限元求解方程為Ka=P。

3 應用實例與分析

3.1 高超飛行器前體考核試驗狀態(tài)的確定

新一代高超聲速飛行器由于升阻比要求，前體要求通常采用尖銳前緣設(shè)計。這樣的設(shè)計會造成更為嚴峻的結(jié)構(gòu)溫升和應力/應變問題，給考核試驗提出了新要求。為更為接近真實飛行情況，考核試驗通常需要選取適合的試驗狀態(tài)參數(shù)。本文提出的耦合分析方法，可以為考核試驗提供合理的狀態(tài)參數(shù)，有較大的實際應用價值。圖3為飛行條件下40 s時刻前體溫度分布情況。

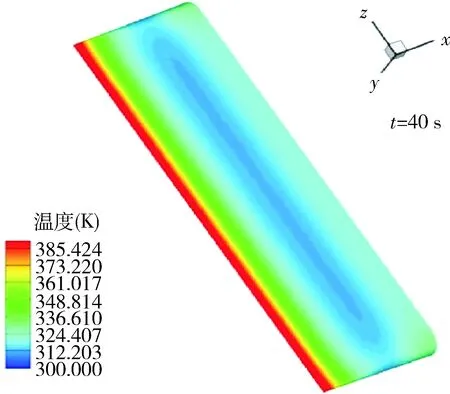
圖3 飛行條件下40 s時刻前體溫度分布Fig.3 Temperature nephogram of leading edge at 40 s

計算試驗狀態(tài)的溫度場時，不同時段的熱流、焓值等參數(shù)是以階躍的形式加載的，實際飛行中熱流、焓值的變化是實時的。這里采用工程方法計算了飛行器沿軌道的表面熱環(huán)境，采用三維數(shù)值方法計算局部部件沿軌道時間的溫度場分布和應力場分布，得到飛行器局部部件沿軌道的溫度和應力分布規(guī)律。根據(jù)該規(guī)律，并考慮地面風洞設(shè)備的實際能力，通過調(diào)整焓值和駐點壓力，計算了不同時間、不同焓值下的飛行器局部試驗件的溫度和應力分布，并與飛行狀態(tài)相對比得到了合適的試驗狀態(tài)參數(shù)。由圖4可知，通過優(yōu)化后，試驗狀態(tài)3的溫升曲線與實際飛行的溫升曲線相差較小。同時，試驗狀態(tài)參數(shù)3得到的熱應力結(jié)果與真實彈道結(jié)果也較為接近。

3.2 高超舵翼結(jié)構(gòu)的多場耦合分析

高超聲速巡航飛行器通常存在舵翼結(jié)構(gòu)，而舵翼結(jié)構(gòu)在發(fā)生偏轉(zhuǎn)或存在迎角情況時會承受較高的氣動力/氣動熱載荷，多場耦合作用顯著。本文采用氣動力、氣動熱、熱響應和熱應力/變形耦合求解的雙向面/體耦合方法進行計算分析。迭代過程中，氣動力計算使用更新外形后的流場網(wǎng)格，此網(wǎng)格由上一輪結(jié)構(gòu)變形計算獲得，從而獲得更新的氣動力載荷。再對考慮了氣動加熱的機翼結(jié)構(gòu)進行熱應力/應變計算，以更新結(jié)構(gòu)變形，直到飛行器結(jié)構(gòu)變形收斂為止。

圖4 試驗狀態(tài)和飛行狀態(tài)駐點溫度對比Fig.4 Stagnation temperature of test status and flight status

圖6為機翼結(jié)構(gòu)最高溫度隨時間變化曲線。從圖10中可以看出，在飛行初期結(jié)構(gòu)溫升較快，隨時間推移，結(jié)構(gòu)溫升趨于平緩，并逐漸達到平衡。非均勻溫升會造成結(jié)構(gòu)熱應力，同時溫升也會造成材料物性改變，從而影響氣動彈性特性。因此，在氣動彈性分析中考慮氣動加熱的耦合影響十分必要。圖7所示即為舵翼結(jié)構(gòu)靜止狀態(tài)、不考慮熱影響的飛行狀態(tài)和考慮熱影響的飛行狀態(tài)(熱氣動彈性)比較圖。可以發(fā)現(xiàn)，氣動加熱對模型氣動彈性特性和結(jié)構(gòu)安全性影響顯著。因此，在結(jié)構(gòu)設(shè)計中應充分考慮結(jié)構(gòu)溫升和應力/應變的影響，合理進行結(jié)構(gòu)設(shè)計和材料使用。

圖5 高超聲速飛行器機翼模型Fig.5 Wing model of hypersonic vehicle

圖6 結(jié)構(gòu)最高/最低溫度隨時間變化曲線Fig.6 Maximum/minimum temperature versus time of wing model structure

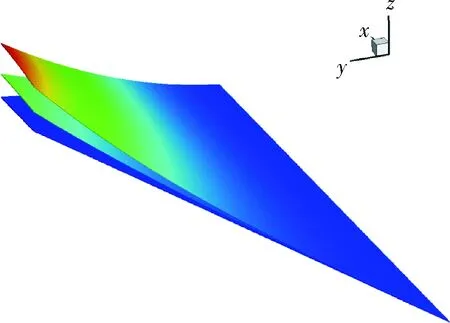
圖7 靜止/氣彈/熱氣彈狀態(tài)機翼結(jié)構(gòu)形變示意圖Fig.7 Deformation diagram of wing structure in the ground stationary/ aeroelastic/ aerothermoelastic state

3.3 氣動力/熱/軌道綜合優(yōu)化設(shè)計

高超聲速飛行器再入大氣層飛行的特點決定了其氣動布局的設(shè)計優(yōu)化問題是一個多學科的設(shè)計優(yōu)化問題。通過本文的多場耦合分析策略與方法，可形成飛行器氣動力/熱與軌道綜合優(yōu)化設(shè)計能力。以類X-37高超聲速飛行器為例(如圖8)，在考慮軌道和飛行特點的基礎(chǔ)上，選取軌道航程最大和駐點沿軌道總加熱量最小作為優(yōu)化子目標。多目標優(yōu)化時，采用加權(quán)函數(shù)方法確定各目標間的關(guān)系。以ω1和ω2表示兩目標的加權(quán)參數(shù)。幾何設(shè)計變量選取機身球形頭部的半徑Rhd、機身中段的寬度Bw、機身的總高度Bh以及機身尾部兩個擴張段的開始位置x1和x2。

圖8 類X-37參數(shù)化外形Fig.8 Parametric geometrical configurations

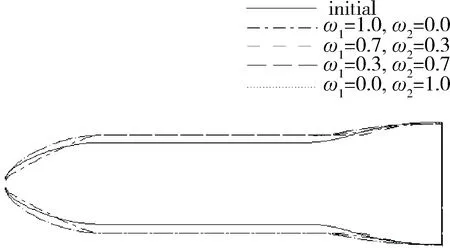
圖9 最優(yōu)布局與初始布局俯視圖比較Fig.9 Top view of the fuselage

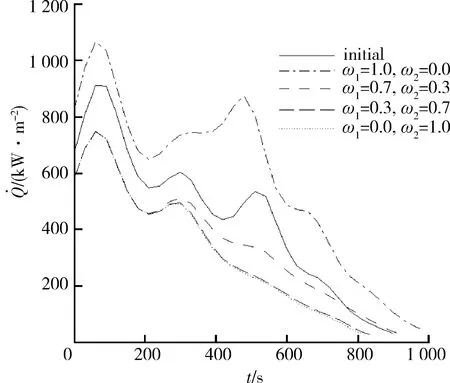
圖10 駐點熱流密度-時間曲線Fig.10 Heat flux of the stagnation point along the trajectory

通過上述分析可以看出，對于不同的子目標加權(quán)系數(shù)，通過優(yōu)化所獲得的最優(yōu)氣動布局和飛行軌道均具有非常明顯的差別。飛行軌道總航程最大和沿軌道的駐點總加熱量最小是兩個相互矛盾的子目標，一個性能的改善通常會給另一個性能帶來一定的損失。在設(shè)計過程中，究竟選取哪種情況作為最終的設(shè)計結(jié)果，還主要依賴于整個飛行任務的需求以及設(shè)計者對于整個任務的總體把握。

4 結(jié)束語

本文主要闡述了熱防護系統(tǒng)中遇到的多場耦合問題，提出了多場耦合分析策略與方法。并采用本文提出的耦合分析方法，對實際工程中遇到的多場耦合問題進行了計算分析。氣動力/熱與結(jié)構(gòu)的多場耦合問題是隨著熱防護系統(tǒng)設(shè)計水平的日益提高而逐步得到認識和發(fā)展的。熱防護系統(tǒng)耦合分析方法的建立將對以下幾方面的研究起到積極作用：

(1) 為飛行器防熱結(jié)構(gòu)的性能準確評估提供有效工具；

(2) 為提高防熱結(jié)構(gòu)設(shè)計精度奠定基礎(chǔ)；

(3) 為飛行器熱氣動彈性問題研究提供技術(shù)支撐；

(4) 為飛行器艙內(nèi)熱管理系統(tǒng)設(shè)計提供較為精確的計算邊界。

參考文獻：

[1] THORNTON E A, DECHAUMPHAI P. Coupled Flow, Thermal, and Structural Analysis of Aerodynamically Heated Panels[J]. Journal of Aircraft ,1988, 25(11): 1052-1059.

[2] CHEN Y K, HENLINE W D, TAUBER M E, Mars Pathfinder Trajectory Based Heating and Ablation Calculations[J]. Journal of Spacecraft and Rockets, 1995, 32 (2): 3-4.

[3] Matthias C Haupt, Reinhold Niesner, Ralf Unger,et al. Computational Aero-Structural Coupling for Hypersonic Applications[C]∥9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. San Francisco, California,2006.

[4] 桂業(yè)偉, 陳蘭, 余澤楚,等. 窗口區(qū)域燒蝕瞬態(tài)熱響應耦合計算與溫升規(guī)律研究[J].工程熱物理學報, 1997, 5(3): 331-335.

GUI Ye-wei, CHEN Lan, YU Ze-chu, et al. The Numerical Simulation of Coupled Unsteady Ablation and Heat Transfer in the Porthole[J]. Journal of Engineering Thermophysics, 1997, 5(3): 331-335.

[5] 桂業(yè)偉, 袁湘江. 類前緣防熱層流場與熱響應耦合計算研究[J], 工程熱物理學報, 2002, 23(6):733-735.

GUI Ye-wei, YUAN Xiang-jiang. Numerical Simulation on the Coupling Phenomena of Aerodynamic Heating with Thermal Response in the Region of the Leading Edge[J]. Journal of Engineering Thermophysics, 2002, 23(6): 733-735.

[6] 耿湘人, 張涵信, 沈清,等. 高速飛行器流場和固體結(jié)構(gòu)溫度場一體化計算新方法的初步研究 [J].空氣動力學學報, 2002, 20(4): 422-427.

GENG Xiang-Ren, ZHANG Han-xin, SHEN Qing, et al. Study on an Integrated Algorithm for the Flowfields of High Speed Vehicles and the Heat Transfer in Solid Structure [J].Acta Aerodynamica Sinica, 2002, 20(4): 422-427.

[7] 黃唐, 毛國良, 姜貴慶,等. 二維流場、熱、結(jié)構(gòu)一體化數(shù)值模擬[J].空氣動力學學報, 2000, 18(1):268-372.

HUANG Tang, MAO Guo-liang, JIANG Gui-qing, et al. Two Dimensional Coupled Flow-Thermal Structural Numerical Simulation[J]. Acta Aerodynamica Sinica, 2000, 18(1): 268-372.

[8] Van Leer B. Flux-Vector Splitting for the Euler Equations[R]. ICASE Report-82-30, 1982.

[9] 朱自強. 應用計算流體力學 [M]. 北京：北京航空航天大學出版社,1998.

ZHU Zi-qiang. The Application of Computational Fluid Dynamics [M].Beijing:Beijing University Press,1998.

[10] Van Leer B. Towards the Ultimate Conservative Difference Scheme V: A Second Order Sequel to Godunov’s Method[J].Journal of Computational Physics, 1979,32:101-136.

[11] 劉磊, 桂業(yè)偉, 耿湘人,等, 高超聲速飛行器熱氣彈靜態(tài)問題研究[J].空氣動力學學報, 2013, 31(5): 559-563.

LIU Lei, GUI Ye-wei, GENG Xiang-ren, et al. Study on Static Aerothermoelasticity for Hypersonic Vehicle[J].Acta Aerodynamic Sinica, 2013, 31(5): 559-563.

[12] LIU Lei, GUI Ye-wei, DU Yan-xia, et al. Study on the Similarity Criteria of Aircraft Structure Temperature/Stress/Dynamic Response[J]. Journal of Thermal Science and Technology, 2012, 7(1):1-10。