基于ABAQUS的飼料料倉結構優化設計

孫健

（江海職業技術學院 機電工程系，江蘇 揚州 225101）

0 引 言

本文以某型號飼料料倉為研究對象，對料倉滿載、料倉下層倉壁的靜力學性能做分析研究，結合料倉的測試進行模型修正，并改進料倉倉壁板的加強筋（壓凸）結構，對料倉的結構進行優化設計。其主要研究內容如下：

1）飼料料倉靜態分析。通過Solid Works 三維造型軟件對飼料料倉下層進行建模，結合散體力學的相關知識，導入有限元分析軟件ABAQUS 中建立鋼結構筒倉有限元模型，利用有限元軟件進行靜態分析。

2）飼料料倉性能測試。根據飼料料倉的結構和工作原理，擬定實驗測試的方案。采用電測法得到各種工況下的應力數據，總體把握飼料料倉的力學性能。將各種工況下的應力與實驗測試結果比較，修正模型結構。

3）飼料料倉結構優化。通過有限元軟件，對倉壁的加強筋進行優化設計，通過倉壁的強度、剛度等指標，達到以同樣的成本，滿足產品更好的性能。

1 料倉的靜力學有限元分析

1.1 料倉模型算例

根據企業要求，剛性料倉高H=19.2 m，倉板高1.5 m，寬1.12 m，彈性模量E=2.1 MPa，泊松比v=0.3。儲料容重1 000 kg·m3，內摩擦角φ=40°，物料與倉壁的摩擦角為10°。采用有限元分析方法，找出結構的最危險點和最大位移變形點,為結構的強度校驗提供了數據支持。

1.2 Solidworks 建模

圖1 上下倉板尺寸

SolidWorks 直接建立飼料料倉的三維模型，又由于本文采用有限元法進行分析，考慮倉壁的柔性以及倉內貯料和倉壁變形間的相互影響，對于金屬倉，考慮倉壁作為殼單元進行分析。因此在SolidWorks中建立的模型為殼體，采用拉伸曲面進行各個面的建立。如圖2 所示。

1.3 ABAQUS 軟件分析

1）將倉壁殼體模型導入有限元分析軟件ABAQUS 中，并對倉壁劃分網格。有限元網格劃分是進行有限元數值模擬分析至關重要的一步，它直接影響著后續數值計算分析結果的精確性。網格劃分涉及單元的形狀及其拓撲類型、單元類型、網格生成器的選擇、網格的密度、單元的編號以及幾何體素［1］。有限元模型如圖3 所示。

圖2 料倉的倉壁建模

圖3 料倉網格的劃分

圖4 整體邊界約束

2）施加邊界約束和載荷。根據實際受載狀況，對螺栓孔和倉壁的底邊進行全約束，如圖4、圖5 所示。

料倉加載情況如圖6 所示。

3）計算并顯示結果。將料倉在約束及載荷確定的情況下進行有限元分析計算，得到其應力云圖，計算分析結果如圖7 所示。

圖5 局部螺栓的邊界約束

2 飼料料倉的應力測試

目前通常采用材料力學和散體力學理論，進行飼料料倉的結構設計，通過大量簡化的計算算法得出設計結果。而構件實際受力情況比較復雜，所以要獲得料倉實際的受力情況，就必須進行料倉倉壁的應力測試。

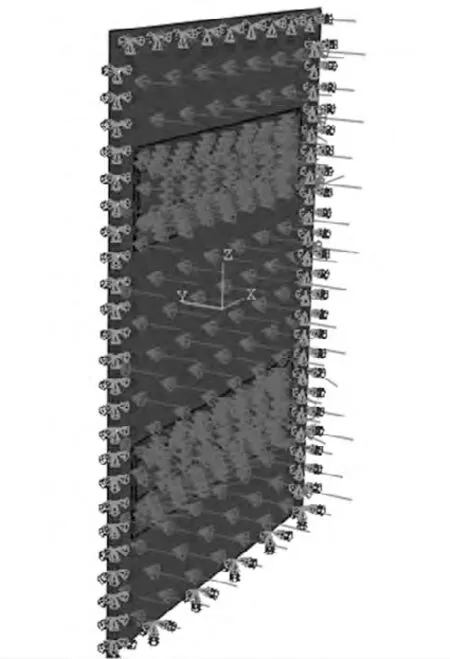
圖6 料倉加載示意圖

2.1 測試原理

應變電測法測試性能穩定、測試方法簡單，所以應用較為廣泛。這種方法在構件的表面分布一定數量的點來進行測量，對于料倉的應力測試采用應變電測法，在實際工程的比較常用。

圖7 整體應力云圖

應變電測法的測試原理就是先測量出構件某個部分受力的變形量，然后應用胡克定律來計算所受應力的大小。其中，電阻應變片是一種電阻式傳感器，通過自身電阻的變化來反映被測構件的機械應變。將電阻應變片組成測量電橋，當橋臂電阻變化時，電橋就輸出一個與其變化大小成線性關系的電壓。通過應變儀對該電壓進行放大，并對電阻應變片的靈敏度系數進行歸一化，就能使輸出的電壓大小和實際應變大小相對應，從而確定構件應力情況［2］。

2.2 應力狀態分析及應力數值的計算

1）單向應力狀態。在測得應變值ε 后，由胡克定律公式σ=Εε 來計算出相應的應力數值，再根據構件的幾何形狀大小計算出所受的載荷。

2）平面應力狀態。許多情況下需要測量一般平面應力場內的主應力，其主應力方向可能是已知的，或者未知的，一般采用貼應變花的辦法進行測試，應變花的示意圖如圖8 所示。對于平面應力狀態，如能測出某點三個方向的應變σA、σB和σC，就可以計算出該點的主應力大小及方向［3］。

圖8 應變花示意圖

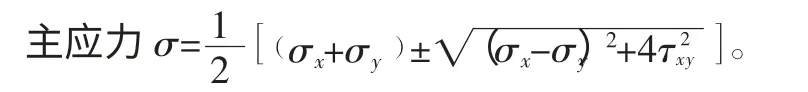
式中，E 為構件的彈性模量，ε 為應變數值。

2.3 測試方案的擬定

采用電測法對倉壁進行應力測試，模擬了實際工況下料倉承受的應力，零應力狀態為料倉載荷為零，再逐步加載至滿載，記錄下各測點的應變數值，通過數據處理得到各測點應力的具體數值。料倉應力測試的測量系統主要由記錄儀器、電路、計算機和電阻應變片等組成，測試框圖如圖9 所示。

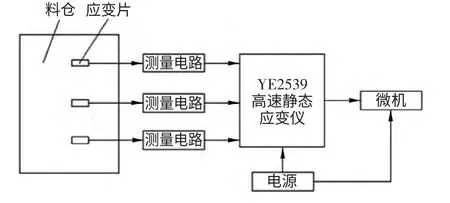
圖9 料倉應力測試框圖

2.4 料倉倉體應力測點示意圖

測點北雙1、北雙3 為兩向應變花，其余均為三向應變花；測點西雙1 為兩向應變花，其余均為三向應變花。圖10 中所有測點均為三向應變花。圖示為北面測點示意圖，南面測點與北面測點對稱布置，用“南1，南2……”編號標注。具體分布和編號如圖10、圖11、圖12 所示。

2.5 測試結果

大倉應力較大點主要分布在大倉東面加強筋下邊兩側位置及中間位置（東2、東6、東9）；大倉南面、北面應力較大點主要分布在焊接處上下兩個加強筋的中間位置（南1、南5、北1、北5）。小倉應力較大點主要分布在小倉西面焊接處上下兩個加強筋的中間位置（西1、西2、西4）。

表1 危險點應力對比 MPa

圖10 料倉北面（南面）應力測點示意圖

圖11 料倉西面應力測點示意圖

圖12 料倉東面應力測點示意圖

3 測試與有限元計算的結果分析

算例中加強筋部分的深度為30 mm，寬度240 mm，加強筋間距為720 mm。將料倉測試結果與有限元計算相比較，測點處的應力及位移值基本吻合，差異較小，驗證了有限元模型的正確性，同時確定了所采取的載荷加載方式是正確的，可以進行下面關于料倉結構的優化設計研究工作。

4 優化設計

優化設計已經廣泛應用于各個領域，能顯著提高經濟效益和社會效益。優化設計是一種尋找確定最優設計方案的技術。所謂“最優設計”是指一種方案可以滿足所有的設計要求，而且所需的支出（如重量、面積、體積、應力、費用等）最小，即最有效的方案［5］。

表2 應力測試值與有限元計算值相比較 MPa

4.1 優化方案

為了盡可能不改變原方案的工藝過程，在優化的時候，主要考慮改變加強筋的形狀和布置。

1）優化方案一：改變加強筋加強筋部分寬度。加強筋寬分別為230 mm、250 mm 和260 mm，應力云圖如圖13、圖14、圖15 所示。

圖13 寬230mm 時應力云圖

圖14 寬250mm 時應力云圖

圖15 寬260mm 時應力云圖

2）優化方案二：改變加強筋部分深度。加強筋深度分別為35 mm、40 mm 和45 mm，應力云圖如圖16、圖17、圖18 所示。

圖17 深度40mm 時正面應力云圖

圖18 深度45mm 時正面應力云圖

3）優化方案三：改變加強筋部分間距。加強筋間距分別為680 mm、700 mm 和740 mm，應力云圖如圖19、圖20、圖21 所示。

4.2 優化結果比較

圖19 間距680mm 時應力云圖

圖20 間距700mm 時應力云圖

圖21 間距740mm 時應力云圖

通過以上三種方案，對加強筋的結構進行了不同的調整，對計算出的結果進行比較，具體優化結果對比見表3。優化結果表明，加強筋的寬度為230 mm，加強筋深度為40 mm 和加強筋間距為680 mm為最佳，改進后的料倉變形及應力都減小了。

5 結 語

本文根據飼料料倉的結構和工作原理，擬定了實驗測試的方案。采用電測法得到了各種工況下的應力數據，先從總體上把握了飼料料倉的力學性能。然后利用三維造型軟件SolidWorks 對飼料料倉建模，通過有限元軟件ABAQUS 進行靜態分析。最后將工況下的應力與實驗測試結果比較，驗證模型分析的正確性。在此基礎上，對本文的算例模型結構進行修正，得到優化方案。

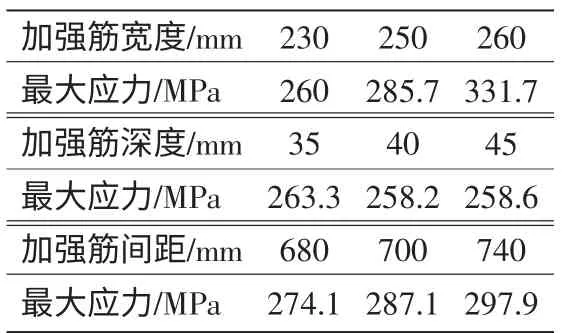
表3 集中優化結果對比

［1］ 姜京偉，程闊.有限元網格劃分剖析［J］.山西交通科技，2007（5）：71-73.

［2］ 劉經燕，王建萍，陳益瑞.測試技術及應用［M］.廣州：華南理工大學出版社，2001：16-20.

［3］ 田萬英.基于有限元的折彎機壓力補償技術研究［D］.揚州：揚州大學，2010：11.

［4］ 陳劍杰，胡永樂，辛春亮，等.鋼筋混凝土結構抗內爆性能的有限元優化設計分析［J］.巖石力學與工程學報，2002，21（4）：554-557.

［5］ 周成軍，沈嶸楓，周新年，等.電動汽車車身結構輕量化研究進展［J］.林業機械與木工設備，2012（11）：16.