基于VB程序的指形齒輪銑刀齒形計算

張杰斌

（太原重工股份有限公司，太原 030024）

0 引 言

漸開線齒輪具有切齒刀具容易制造，互換性好，齒輪中心距的可分離性（即使齒輪傳動中心距有變化，傳動比不變）等諸多優點，因而是目前機械工程中最普遍應用的齒輪。

對于重型機械設備中模數m＞36 mm 的大模數漸開線圓柱齒輪制造，由于采用展成法加工時刀具制造復雜、周期長、成本高，現在廣泛使用仿形法銑削漸開線齒形，因此設計成形銑刀時就必須進行非常復雜的齒形計算，尤其是斜齒圓柱齒輪漸開線齒形更加復雜，人工逐個計算幾十個坐標點效率低下且極易出錯，刀具齒形精確成為保證齒輪加工精度的首要條件。為了提高計算精度，簡化刀具設計過程、縮短制造周期，開發指形齒輪銑刀齒形計算程序具有實用性和緊迫性。鑒于VB 具有開發圖形用戶界面（GUI）優越，使用性及可讀性強的優點，我們采用VB 軟件，結合指形齒輪銑刀齒形計算方法開發了“基于VB 的指形齒輪銑刀齒形計算程序”。該程序適用于各種直齒和斜齒圓柱齒輪的指形銑刀齒形計算，具有很好的實用性。本文結合計算實例，簡要介紹該程序的編制與操作過程。

1 齒輪銑刀的漸開線齒形

漸開線齒輪的齒形由兩部分組成：工作部分和非工作部分。工作部分為漸開線；非工作部分為過渡曲線。漸開線部分在齒輪工作中是參與嚙合部分，因此，要求這部分曲線一定要準確無誤，才能保證正確嚙合。完整的過渡曲線又由直線部分和齒根圓角部分組成。

對于直齒圓柱齒輪，其齒形漸開線是當發生面繞基圓柱作純滾動時，發生面上與齒輪軸線平行的直線上各點的軌跡集合。因此，可以按照漸開線標準公式求解出正確的齒形輪廓上任意點M 的橫、縱坐標值xg、yg，如圖1所示。由于指形銑刀在加工直齒輪時是按仿形法原理進行切削的，故其齒形與被加工齒輪的齒槽形狀完全相同。

圖1 直齒任意點M 的齒形坐標

對于斜齒輪的齒廓曲面，如圖2（a）所示，斜齒輪漸開線是當發生面繞基圓柱作純滾動時，發生面上與齒輪的軸線成一交角βb的直線K-K 上各點軌跡的集合。其具有以下特征：1）斜齒輪的螺旋角β 是齒廓曲面與分度圓柱面相交的螺旋線的切線與齒輪軸線之間所夾的銳角；2）斜齒輪的端面齒廓為精確的漸開線，如圖2（b）；3）直線K-K 所形成的曲面為一漸開螺旋面；4）基圓柱面以及和它同軸的圓柱面與齒廓曲面的交線都是螺旋線，但其螺旋角不等。

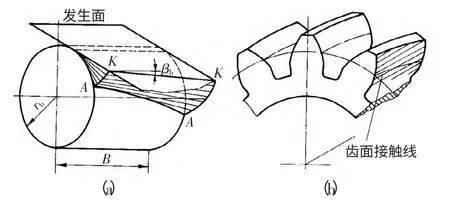
圖2 斜齒圓柱齒輪漸開線原理圖

由圖可見，斜齒輪由于齒向的傾斜，它的每一個基本參數都可以分為法面參數和端面參數。由于用指形銑刀加工斜齒輪，刀具都是沿輪齒的螺旋齒槽方向運動，并且刀具齒形的法面基本參數為標準值，所以設計、加工和測量斜齒輪時均以法面為基準。由于銑刀刀刃上各組成點是在不同平面內與齒面接觸，它們的接觸線為一條空間曲線，因此，銑刀軸向截面中的齒形，與齒輪端截面和法截面中的齒形均不相同。由此可知，把齒輪法向截面中的當量齒輪齒形作為銑刀齒形的做法是不精確的。

加工斜齒圓柱齒輪的銑刀齒形，應按無瞬心包絡法原理求得。在確定銑刀齒形時，假設齒輪不動，指形銑刀繞齒輪軸線旋轉并沿軸線移動。在作相對螺旋運動的某一瞬時，齒輪端面齒形給定點的螺旋表面的法線與銑刀的軸線相交，從接觸點到銑刀軸線的最短距離，即為銑刀齒形的橫坐標。由此原理可推導出斜齒輪指形銑刀齒形計算步驟：

ms=mn/cos βf；αfs=arctan（tanαfn/cos βf）；r0=rfcos αfs；ωfs=π/（2z）-2ξtan αfn/z+ΔS/（mszcos βf）；ωos=ωfs-invαfs；λ0=arctan［1/cos αfstan βf］，αes=arcos（r0/Re）；αis=arcos（r0/Ri）；a=r0sin λ0（invαy+ωos）；Ω=arcsin（sin λ0sin αy）；x=acos Ω；

當r0＜Ri時，y=r0/cos αy-asin Ω-Ricos ωis；

當r0≥Ri時，y=r0/cos αy-asin Ω-Ri。

其中：ms為端面模數；mn為法向模數；z 為齒數；βf為分圓螺旋角；αfs為端面分圓螺旋角；αfn為法向分圓螺旋角；r0為基圓半徑；rf為分圓半徑；ωfs為端面分圓齒間中心半角；ωos為端面基圓齒間中心半角；ξ 為變位系數；ΔS 為齒厚減薄量；λ0為基圓螺旋角；αes為端面頂圓壓力角；αis為端面根圓壓力角；αy為參數角；Re為齒頂圓半徑；Ri為齒根圓半徑；a 為齒形坐標點距離螺旋面法線長度；Ω 為螺旋面法線與銑刀軸截面的夾角；x 和y 分別為齒形各點的橫、縱坐標值。

程序計算時，按齒形曲線的高度方向逐個選取一系列 參數角代入運算，得出相應點的x 和y 坐標值。αy值的選取，由齒形圖可見，其取值區間應使計算的坐標點y 值在齒輪的齒頂圓和齒根圓范圍內，這樣可以保證計算出的每個坐標點存在于齒形的有效輪廓內。參數角αy的最大和最小角度：

αymax=αes+10°；

當ro＜Ri時，αymin=ωos+tan αis；

當ro＞Ri時，αymin=ωos。

其中，αymix為最大參數角，αymin為最小參數角。

齒根圓半徑R 按表1 取值。表1 中K 為齒形漸開線起始點的斜率。

表1 齒根圓角半徑R 取值

這樣就得出了斜齒圓柱齒輪銑刀齒形的計算結果。對于直齒圓柱齒輪，可以作為螺旋角為零度的斜齒輪進行齒形運算，以上計算方法同樣適用。

2 編制基于VB 的指形齒輪銑刀齒形計算程序

程序界面由參數輸入和計算輸出兩部分組成，參數輸入部分包括程序計算所用的齒輪法向模數、壓力角、螺旋角、變位系數、齒厚減薄量等各項參數；計算輸出部分包括參數角αy、齒形各點的X、Y 坐標值、漸開線起點斜線傾角、齒底圓弧半徑等計算結果。該程序具有以下特點：

1）適用性廣。程序可以滿足各國不同齒制的直齒和斜齒指形齒輪銑刀的齒形計算要求。

2）可修改性強。通過參數輸入窗口，每個輸入的參數均可獨立修改后反復進行計算。一個齒形計算完成后點擊“輸入數據”按鈕，可將全部輸入和輸出數據清零，開始進行下一個齒形的計算，直至完成所有齒形計算任務。

3）可讀性好。操作界面簡潔整齊、一目了然，不同的用戶均能輕松掌握使用方法。

4）計算精準。經過幾十例齒輪加工的實際使用，計算結果快速精確，特別是對斜齒圓柱齒輪的復雜坐標運算尤為出色，避免了人工計算的緩慢和誤差，極大縮短了指形齒輪銑刀的設計周期。

3 程序計算實例

利用VB 程序計算漸開線銑刀齒形時，可直接運行“圓柱齒輪齒形坐標計算”程序，通過輸入或修改相關參數，如法向模數、齒數、螺旋角、運算步長等，即可得出計算結果，后期可以通過函數接口將計算坐標轉換為CAD圖形。

1）進入運算界面，輸入齒輪參數，見圖3。

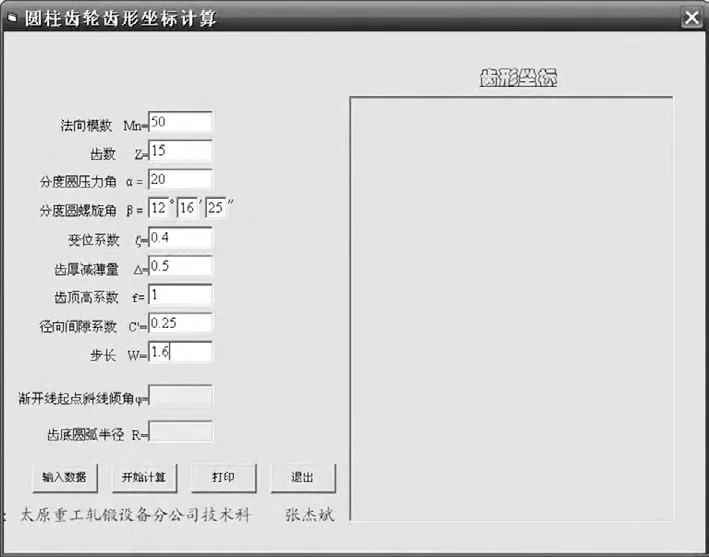
圖3 輸入齒輪參數

2）計算得出指形齒輪銑刀的齒形坐標，見圖4。

3）繪制指形齒輪銑刀坐標圖形，見圖5。

圖4 輸出銑刀齒形坐標

圖5 指形齒輪銑刀齒形圖

4）經實際使用驗證，計算結果得出的齒形坐標與手工計算結果一致。若輸入的螺旋角為零度，則輸出為直齒指形銑刀的齒形。因此，該程序在對漸開線銑刀齒形計算中是準確的。輸出的齒形坐標可直接用于指形齒輪銑刀等仿形刀具的刃形設計。

4 結 語

通過總結歸納齒輪仿形法加工經驗，開發了基于VB的指形齒輪銑刀齒形計算程序，使用該程序能迅速精確地求解指形齒輪銑刀等仿形法刀具的齒形數據，且具有很好的實用性和通用性。文中所介紹的方法操作方便，簡化了計算過程，縮短了計算周期，提高了銑刀設計效率，實現了指形齒輪銑刀的精益設計。

［1］ 齒輪制造手冊編輯委員會.齒輪制造手冊［M］.北京：機械工業出版社，1998.

［2］ 四川省機械工業局.復雜刀具設計手冊［M］.北京：機械工業出版社，1979.

［3］ 璩柏青，何安年，杜淑莘.斜齒圓柱齒輪指形銑刀CAD［J］.工具技術，1997（8）：15-18.

［4］ 田培棠.加工漸開線螺旋齒輪的指狀銑刀齒形計算［J］.工具技術，1979（1）：51-55.

［5］ 許唯沖.指形齒輪銑刀的設計、制造與使用［J］.工具技術，1995（10）：8-10.

［6］ 趙文濤，陳濤.漸開線齒形誤差測量方法［J］.機電產品開發與創新，2009，22（5）：119-121.