基于多目標拓撲優化的失效零件再設計

孫 哲，胡于進

（華中科技大學機械科學與工程學院，湖北 武漢430074）

0 引言

在當今的工業設計中，零部件結構創新設計和輕量化設計成為當前機械設計的一個重要的方向。拓撲優化已成為實現零部件結構創新設計和輕量化設計的重要工具，被廣泛運用于建筑、航空航天、汽車、海洋工程和船舶制造等領域［1－2］。

近些年來，拓撲優化的應用逐漸增多［3－5］。但是，參考文獻［3－5］都是通過選擇一個主要目標進行單目標優化，沒有考慮到在復雜多工況多目標情況下的拓撲優化設計。由于設計問題的復雜性，必須滿足的設計指標往往是多方面的，因此，多目標優化是工程設計的一個基本問題。在多目標拓撲優化中，孫曉輝［6］，范文杰［7］等提出運用數學規劃法將多目標的拓撲優化問題轉換為單目標的拓撲優化，通過加權規劃法將多目標的拓撲優化轉變為單目標優化，但是如何選擇合適的權重仍是一個難點。

耿玉磊［8］等總結了求解多目標優化的幾種方法，提出將模糊理論和滿意度應用于多目標優化中。基于這一思想的啟示，結合模糊理論，提出了一種基于模糊滿意度和加權平方和法的變權重多目標拓撲優化，利用子目標函數的模糊滿意度構造其權重，實現了各子目標函數權重的動態調整，解決了權重難以選擇的問題。

1 基于模糊滿意度的變權重多目標規劃方法

1．1 模糊滿意度

模糊理論是處理不確定問題的理論基礎，已成為解決多目標優化問題的一種有效工具，其基本思想是將目標函數模糊化，引入隸屬度函數，將優化目標的最優解轉換為尋找目標模糊集中的滿意解。假設多目標優化問題表達為：

用各個約束條件對各個單目標fi（x）進行優化（式（2）），求解得到該目標的最優解以及其他目標函數的值，結果如表1所示。

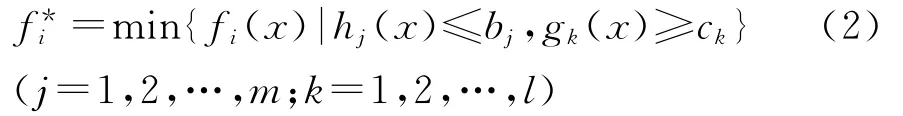
表1 單目標優化結果

表1矩陣對角線的元素fii（x）即fi（x）目標的理想點，定義表1各列中離理想點最遠的點為，并為目標fi（x）的悲觀點。和組成理想點和悲觀點向量，多目標優化的過程就是在理想點和悲觀點組成的n維長方體中尋找滿意解［9］。

將子目標函數模糊化，對于每個目標函數fi（x），i＝1，2，…，n，給出相應的模糊伸縮指標di（di＞0）。伸縮指標的取值根據該目標可以接受的最差解與理想解的差值來選擇，定義目標函數隸屬函數格式為［10］：

隸屬函數值λi反映了目標函數fi（x）的值在該目標的模糊集中接近理想點的程度，定義λi為第i個目標的模糊滿意度，表示該目標在模糊目標集的隸屬程度。

1．2 基于模糊滿意度的變權重多目標規劃法

加權平方和方法是求解多目標優化的一種常用的方法，對于1．1節所給的多目標優化構造出加權平方和法的評價函數為：

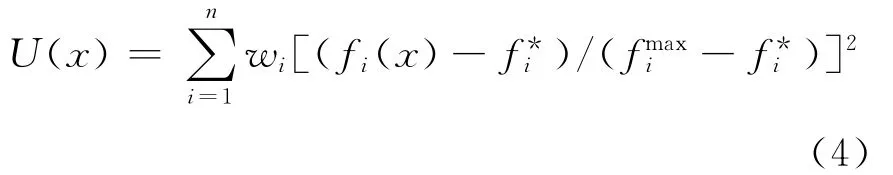
根據式（3）的模糊滿意度來確定各個子目標的權重，權重會根據子目標函數值確定，此時權系數wi是動態的。選擇權系數為：

使用模糊滿意度來確定加權系數，可以根據各個目標在模糊集中的滿意度來動態地調整目標的權重，滿意度較小的目標權重加大，使該目標可得到較好的優化。此外，子目標模糊化的伸縮指標是通過每個目標可接受最差解來確定的，這樣可以控制優化后的各個目標值盡量落在自己期望的范圍之內。

1．3 多目標拓撲優化

在多工況下，每個工況都對應著一個剛度最優的拓撲形狀。因此，多工況剛度優化問題屬于多目標拓撲優化。通常把剛度最大問題轉化為柔度最小問題來處理來定義，柔度則用應變能來定義。

多工況的剛度最大化拓撲優化問題描述為：

fj為最小的第j階模態；v為優化后的體積比，用來控制優化得到的最大體積。

每個工況的剛度最大化優化模型為：

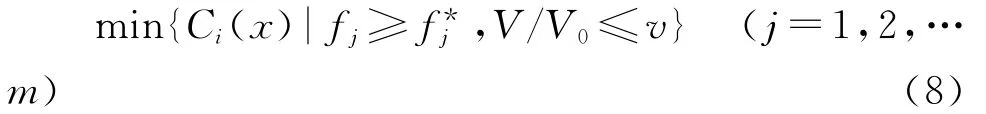
由于零件輕量化設計成為當前設計工作的一個需要考慮的因素，所以體積最小化也要作為一個設計目標。體積最小化問題一般描述為：

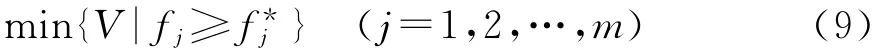
根據式（3）寫出各個目標函數的隸屬函數為：

在Optistruct中求解單目標優化（8）和（9），得到如表1所示的矩陣表。確定理想點和V＊，悲觀點和Vmax，根據各個目標函數允許的最差解，選擇合適的伸縮指標di和dV。由式（10）和式（11）得到模糊滿意度的表達式，由式（4）和式（5）得到多目標拓撲優化的評價函數為：

多工況和體積的多目標拓撲優化的表達式為：

2 汽車零件優化設計

2．1 原零件分析

發動機右上中支架的原始模型如圖1所示。材料參數：彈性模量E＝74 GPa，泊松比u＝0．33，彈性極限Re＝160 MPa，要求零件的質量小于680 g，第一階模態大于650 Hz。

圖1 發動機右上中支架原始設計模型

零件計算模型如圖2a所示，支架底端采用5個彈簧單元模擬與之接觸零件的剛度，彈簧底端固定，零件之間采用螺栓連接，螺栓使用梁單元和剛性單元進行模擬。在X和Z方向，分別受到1 800 N和3 770 N的載荷。對部件進行模態分析和2種工況下的靜力學分析。得到原始零件的一階模態為671．6 Hz，滿足設計要求。由于螺栓采用梁單元和剛性單元來模擬，所以在和剛性單元連接的部分會產生相對于其他單元較大的應力，因此，在應力顯示的時候，沒有考慮凸臺以及其他與簡化螺栓相連接單元的應力，這樣比較真實地反應了零件的應力水平分布。X方向載荷作用下的應力分布如圖2c所示，最大應力為41．5 MPa。Z方向載荷作用下的應力分布如圖2d所示，最大應力為154 MPa。在試驗過程中，零件發生斷裂，如圖2b所示，可以看到斷裂的地方剛好發生在應力過大的地方。由上述分析可知，零件在載荷作用下的應力過大而導致使用過程中的疲勞斷裂。再設計過程中，需要考慮零件的剛度要足夠大，同時考慮到輕量化設計，零件的體積也要足夠小。即需要達到2個剛度最大化和體積最小化這3個目標，所以要用到多目標優化。

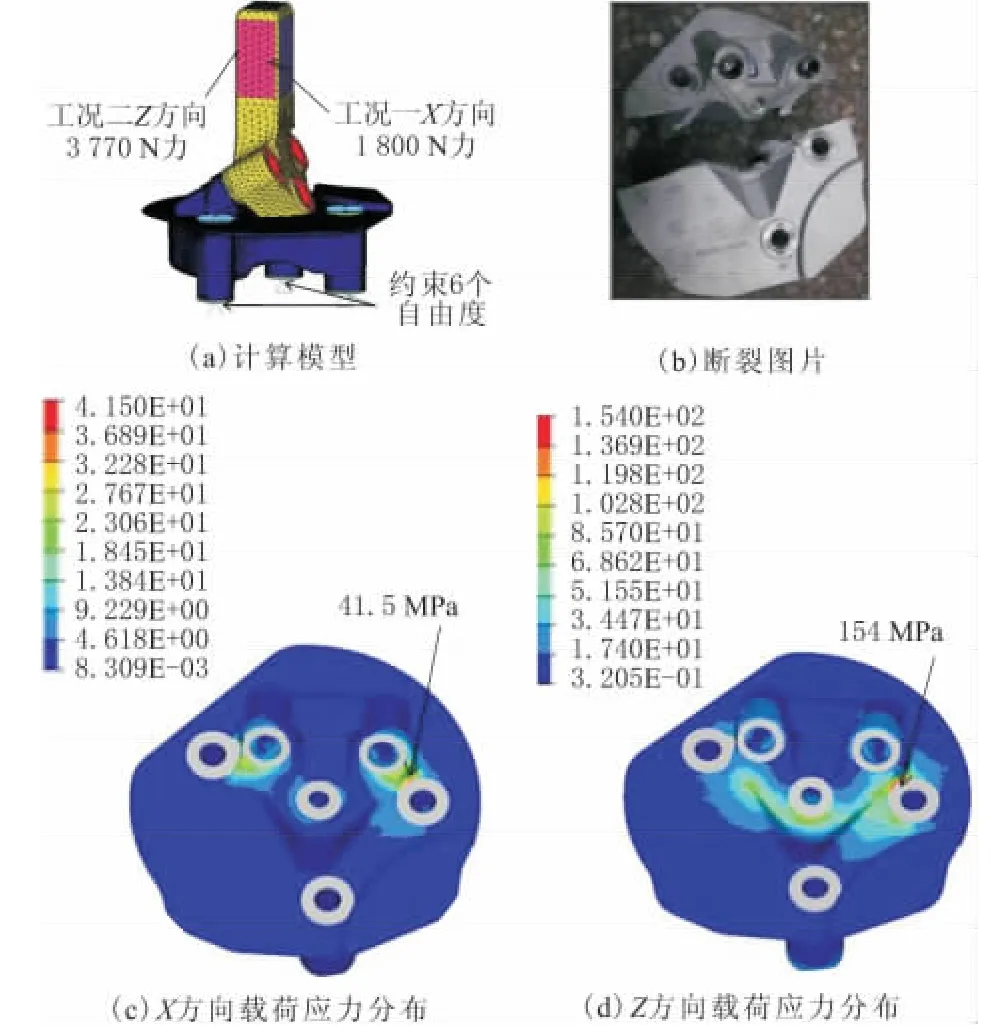
圖2 原始設計應力水平分布和斷裂圖片

2．2 多目標拓撲優化

零件的設計區域和非設計區域如圖3a所示。考慮到發動機左上中支架的裝配要求，僅對下面的加強筋區域進行拓撲優化。首先將加強筋部分全部填滿作為設計區域，優化約束為第一階模態和體積比。由于設計要求最小一階模態為650 Hz，零件最大質量為680 g，考慮到誤差余量，取最小第一階模態為660 Hz，體積比最大為0．2。對2種工況分別進行單目標拓撲優化得到各個工況柔度，優化得到的值為這2個目標的期望值。以體積最小化為目標進行單目標拓撲優化，得到體積的期望值和2種工況的柔度。計算得到表2所示的參數。

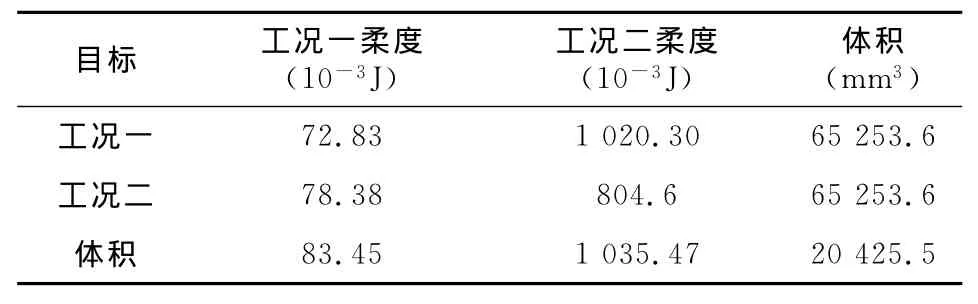
表2 計算各個工況得到的參數

根據表2選擇對角線值為各個目標的理想點，各列最大值為悲觀點。根據實際情況中目標允許的最差解，選擇伸縮指標。理想點、悲觀點和伸縮指標如表3所示。

根據表3數值和式（10）～式（13），使用 Hyper－Math編寫目標函數和所需參數的表達式，將Hyper Math函數作為Optistruct進行拓撲優化的外部響應。在迭代過程中零件的材料分布變化如圖3所示，材料分布不斷得到優化，最終得到如圖3c所示的拓撲形狀。

表3 選擇各個期望值和伸縮指標

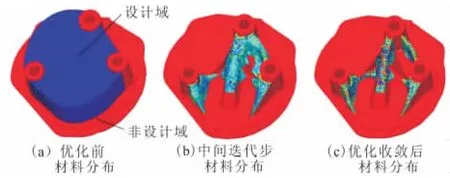
圖3 迭代過程中材料分布變化

優化過程中規劃目標和各個子目標的迭代曲線如圖4所示。規劃目標和各個子目標都能很快達到收斂，各個子目標都在模糊集內，且有較好滿意度。

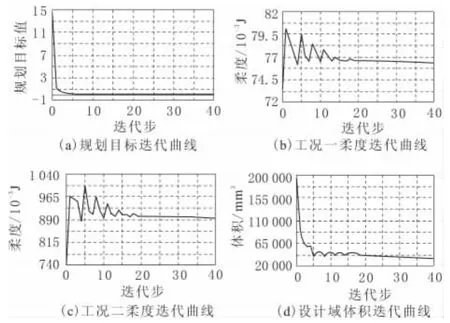
圖4 拓撲優化過程中各個目標的迭代曲線

根據最終優化的拓撲形狀（圖3c），在Pro／E中重新建模，得到如圖5所示的發動機右上支架新設計模型。

圖5 發動機右上中支架新模型

2．3 新零件的分析驗證

對新零件進行分析，得到第一階模態為704 Hz，比優化前的增加了32．4 Hz。

通過拓撲優化使得零件的剛度和動態性能都得到了改善，并且減少了零件的質量，拓撲優化前后比較如表4所示。優化后的新零件比原始零件的應力減少了47．1%，質量減少了7．9%

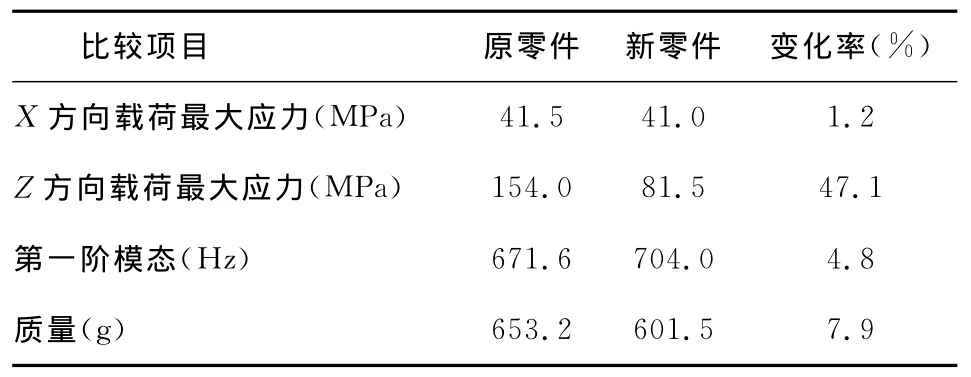
表4 優化前后的比較

3 結束語

模糊理論與加權平方和法結合的基于模糊滿意度的變權重多目標規劃方法，可以很好地求解多目標優化問題，通過改變權重在計算中優先優化那些遠離模糊集的目標，并且使得優化的各個目標的模糊滿意度盡量大，使優化后得到的目標值更靠近理想點。另外，通過模糊滿意度可以控制優化的各個目標值都在自己期望的范圍之內。最后，使用該方法對一個汽車零件結構進行多目標的拓撲優化，使得零件在各個工況下的應力滿足要求，應力分布更加均勻，同時提高了零件一階模態，使得零件具有了更好的動態性能。

［1］ 周克明，李俊峰，李 霞．結構拓撲優化研究方法綜述［J］．力學進展，2005，35（1）：69－76．

［2］ 洪清泉，趙 康，張 攀．OptiStruct ＆ HyperStudy理論基礎與工程應用［M］．北京：機械工業出版社，2012．

［3］ 朱劍鋒，林 逸，陳瀟凱，等．汽車變速箱殼體結構拓撲優化設計［J］．吉林大學學報（工學版），2013，42（3）：584－589．

［4］ Kaya N，Karen，ztürk F．Re－design of a failed clutch fork using topology and shape optimization by the response surface method［J］．Materials and Design，2010，31（6）：3008－3014．

［5］ Kilian S，Zander U，Talke F E．Suspension modeling and optimization using finite element analysis［J］．Tribology International，2003，36（4）：317－324．

［6］ 孫曉輝，丁曉紅．結構多目標拓撲優化設計［J］．機械設計與研究，2012，28（4）：1－4．

［7］ 范文杰，范子杰，蘇瑞意．汽車車架結構多目標拓撲優化方法研究［J］．中國機械工程，2008，19（12）：1505－1508．

［8］ 耿玉磊，張 翔．多目標優化的求解方法與發展［A］．福建省科協第四屆學術年會——提升福建制造業競爭力的戰略思考專題學術年會論文集［C］．2004．109－112．

［9］ 高濟眾，呂新生．交互式滿意協調法——一種多目標優化方法［J］．合肥工業大學學報（自然科學版），1989，12（2）：32－39．

［10］ Luo Z，Chen L P，Yang J，et al．Fuzzy tolerance multilevel approach for structural topology optimization［J］．Computers and Structures，2006，84（3）：127－140．