基于相對高程異常的GPS高程擬合方法探討

陳艷紅，馬全明，劉瑞敏，毛曉康

(1.石家莊經濟學院，河北 石家莊 050031；2.北京城建勘測設計研究院有限責任公司，北京 100101；3.中南大學，湖南 長沙 410083)

基于相對高程異常的GPS高程擬合方法探討

陳艷紅1，馬全明2，劉瑞敏2，毛曉康3

(1.石家莊經濟學院，河北 石家莊 050031；2.北京城建勘測設計研究院有限責任公司，北京 100101；3.中南大學，湖南 長沙 410083)

在傳統二次曲面GPS高程擬合的基礎上，提出一種基于相對高程異常的GPS高程擬合方法。該方法首先通過相對正常高高程異常值的改正，把GPS點的相對大地高轉化為相對正常高，然后將相對正常高與已知點的正常高高程連算，按照傳統的水準測量計算方法平差解算，即能得到最優解的正常高。采用某山區工程實例數據進行了驗證，表明該方法在地勢起伏較大的測區比二次曲面擬合得到的精度要高。

大地高；正常高；GPS高程擬合；高程異常

一、引 言

近年來，GPS衛星定位技術已在測繪領域得到廣泛應用，它不僅能獲取高精度的平面位置，而且能獲得高精度的大地高，如果將大地高轉換為我國采用的正常高，代替部分的傳統水準作業，具有較大的經濟效益[1]。

目前，對GPS高程數據進行轉換的常用方法有物理重力法和幾何解析法兩種。在實際工程應用中，由于無法獲得必要的重力數據，故重力法難以普及[2]。因此，在工程應用中以幾何解析法居多，其主要包括解析多項式法、加權均值法、多面函數法及近年來非常流行的神經網絡法等[3-10]。這些 GPS高程擬合方法的精度受到聯測水準點在測區的分布情況和數量的限制，只考慮了高程異常與點的位置間的關系，而沒有考慮高程異常與點的高程間的關系。本文在GPS高程擬合時不僅考慮高程異常與位置的關系，以及與大地高的關系[11]，并提出了基于相對正常高高程異常的GPS高程擬合模型。

二、基于相對正常高高程異常的GPS高程擬合原理

由于原有GPS高程擬合精度受到聯測水準點在測區的分布情況和數量的限制，只考慮到高程異常與點的位置有關，而沒有考慮到高程異常與點的高程的關系。因此本文在傳統二次曲面GPS高程擬合的基礎上，不僅考慮高程異常與位置的關系，還考慮與相對大地高的關系。

原有GPS高程擬合思路是先求出高程異常ζ，然后把大地高轉化為正常高。本文在擬合時不求高程異常ζ，而是先把GPS點的相對大地高轉化為相對正常高，須加一個改正數，即相對正常高高程異常值。在得到相對正常高高程后，再與已知點的正常高高程連算，按照傳統的水準測量計算方法平差解算，就能得到最優解的正常高。

1.GPS相對大地高高程轉化為相對正常高高程

將GPS大地高程數據轉化為水準測量的相對正常高高程Δh0，即

式中，HA、HB分別表示A、B兩點的大地高，大地高即GPS數據中的高程數據；分別表示A、B兩點的正常高，即我國使用的高程系統；ΔhAB表示A點到B點的相對大地高，即 A、B兩點的大地高差；表示A點到B點的相對正常高高差，即A、B兩點正常高高差；ζAB表示A點到B點的相對正常高高程異常，即A、B兩點的高程異常值的差值。

從式(1)中可以看出，只要得到兩點的相對正常高高程異常ζAB，就可以把GPS大地高程數據轉化為兩點的相對正常高，再根據兩點的相對正常高和已知點的正常高進行連算，利用間接平差進行計算，就可以得出測區所有點的正常高高程，把GPS大地高轉化為正常高高程。

2.相對正常高高程異常求解

(1)建立相對正常高高程異常ζij模型

根據相對正常高高程異常ζij不僅與點的位置有關系，還與相對大地高有關，建立如下函數模型

式中，ζij表示i點到j點的相對正常高高程異常，ζij＝ζj－ζi；Δhij表示i點到j點的相對大地高高程，Δhij＝Hj－Hi；(Xj，Yj)表示j點平面坐標。

在測區中選定一個起始點，所有點的相對正常高高程異常都是基于這一個點的。這個起點最好選在測區的中間。

為了便于擬合計算，對上面的函數模型具體化，ζij與Δhij、Xj、Yj多項式關系為

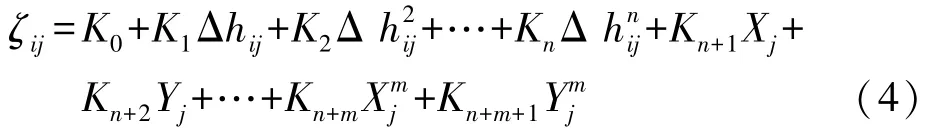
式中，Ki(i＝0，1，…，n＋m＋1)為系數。

對于不同的測區，根據已知數據來選擇系數Ki的個數。

(2)相對正常高高程異常ζij的求解

利用已知點的平面坐標、大地高和正常高的數據按最小二乘法求解系數K。根據式(4)計算未知點的相對正常高高程異常的步驟如下：

1)明確測區已知點的個數，來確定式(4)中的系數K的個數，K的個數要少于已知點的個數。

2)在測區里選定一個起始點，計算其他已知點相對起始點的相對大地高高程、相對正常高高程和相對正常高高程異常，再利用間接平差按最小二乘法求解系數K。

3)計算待擬合點相對于起始點的相對大地高Δh起始點到未知點，然后代入式(4)中可求得待擬合點相對起始點的相對正常高高程異常。

3.GPS相對大地高轉化為相對正常高

求解待定點相對于起始點的相對正常高高程異常后，通過式(2)求得待定點相對起始點的相對正常高，即

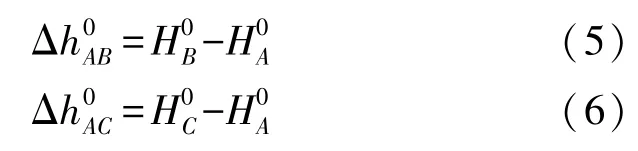
利用式(5)—式(6)就可以得到B、C兩點的相對正常高。這樣就能把待定點相對于起始點的相對正常高轉化為任意兩個待定點間的相對正常高。

4.相對正常高求解正常高高程

求得的兩點間相對正常高和已知點的正常高高程數據按下列公式計算就得到待定點的正常高高程。

上式求出的待定點的正常高高程，由于待定點可以由不同的已知點來推求，這樣就存在多余觀測數據，利用平差計算優化待定點的正常高高程解。

三、實例數據分析

為了驗證相對正常高高程異常的GPS高程擬合方法的可行性，本文采用二次曲面擬合的方法進行比較驗證。某山區測區控制點共有15個，控制點的示意圖如圖1所示，在該區選取了平均對稱的7個已知點，具體數據見表1，其余8個點作為待擬合點，具體數據見表2。

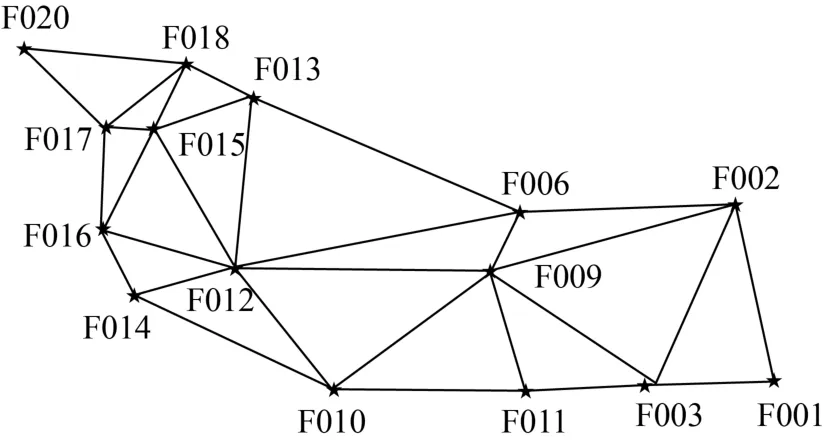
圖1 山區GPS控制點示意圖

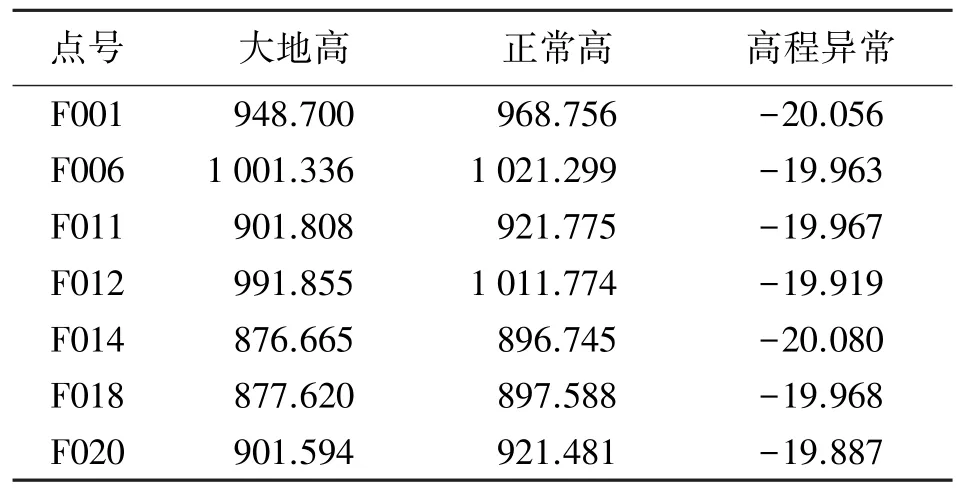
表1 7個已知點的數據 m

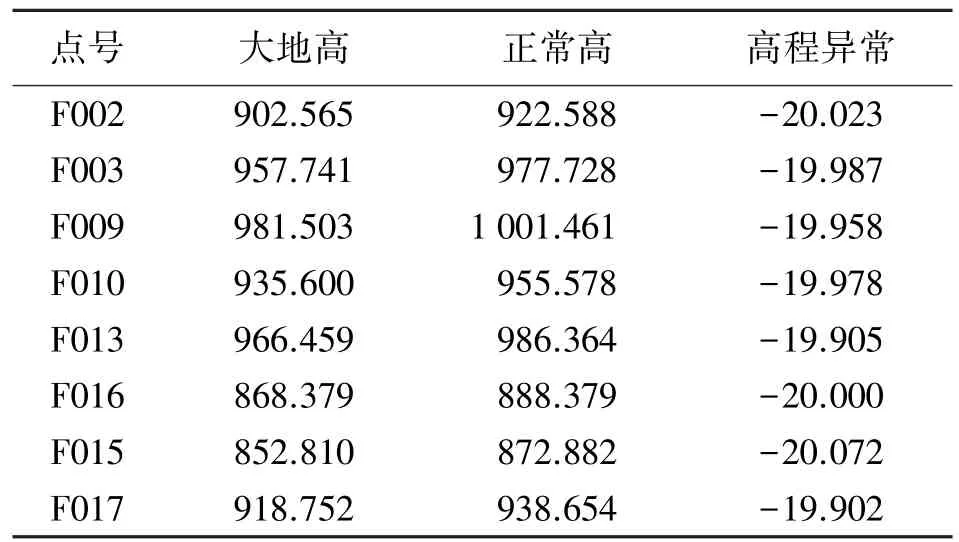
表2 8個待擬合點的數據 m

1.利用二次曲面進行GPS高程擬合

采用二次曲面擬合，用Matlab 7.0實現其算法，得到了8個待擬合點的正常高(見表3)，內部符合

精度為1.4 cm，外部符合精度為23.0 cm。

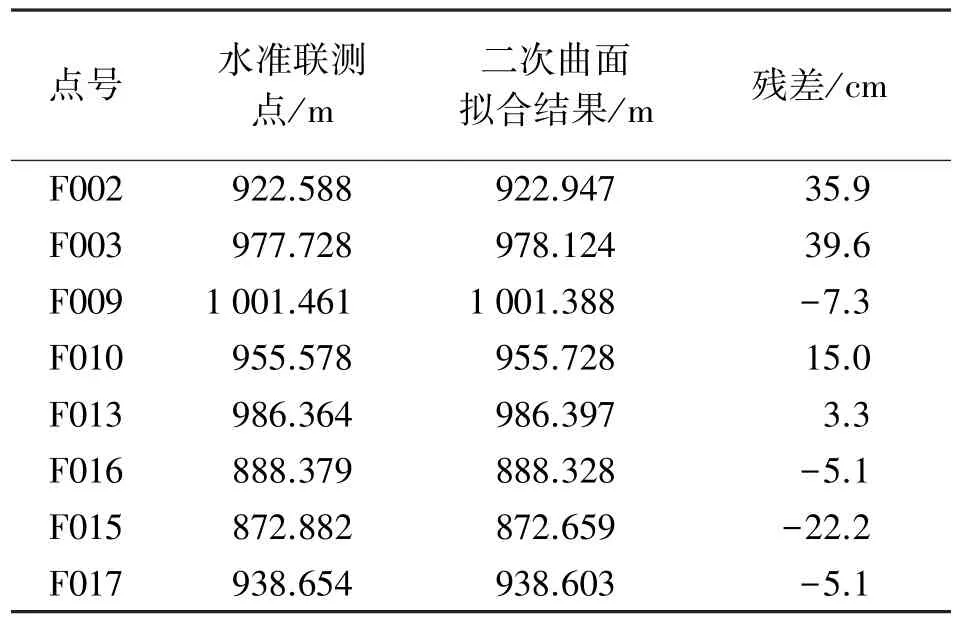
表3 二次曲面擬合結果

2.基于相對正常高高程異常的GPS高程擬合

選取F012作為起始點，根據待擬合點和已知點組合的控制網模型，列出間接平差方程，求解待擬合點的正常高見表4，其內部符合精度為4.3 cm，外部符合精度為2.74 cm。3.二次曲面擬合與相對正常高高程異常擬合對比

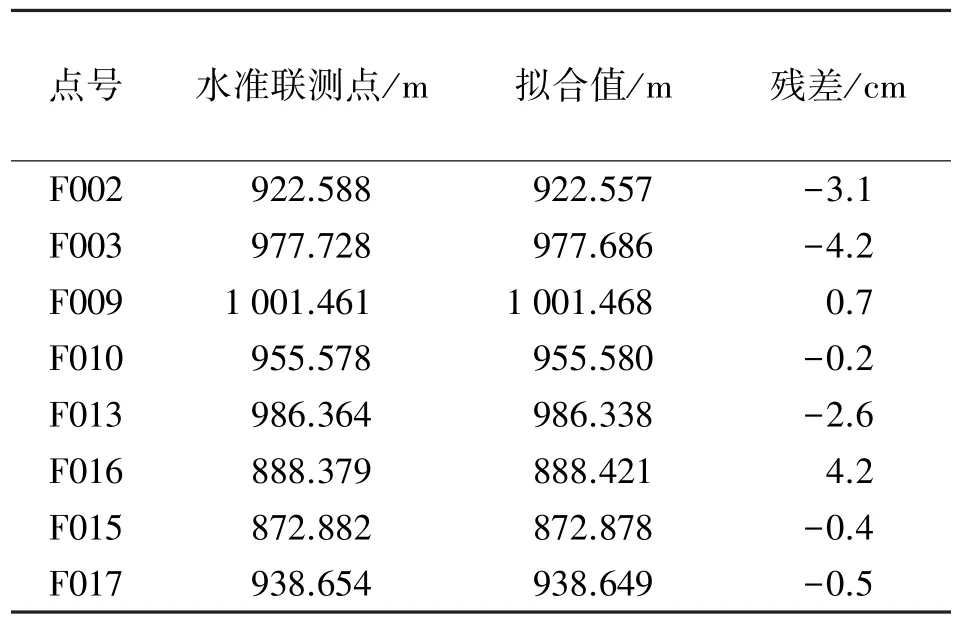
表4 8個待擬合點結果

由表3、表4可以明顯地看出，利用相對正常高高程異常的GPS高程擬合得到的待定點的精度好于傳統的二次曲面擬合，其最大的殘差為4.2 cm。測區的GPS點之間的平均邊長在2 km左右，最大殘差為4.2 cm，在普通幾何水準測量誤差允許殘差范圍內。在地勢起伏較大的地區應用二次曲面擬合，其精度有的很差。從表中可以看出，二次曲面擬合的內符合精度很高但外符合精度很低，這是由于山區的高程異常變化大所決定的。

通過對比，充分地說明了基于相對正常高高程異常的GPS高程擬合在處理山區的數據時能明顯地提高GPS高程擬合的精度。

四、結束語

傳統的GPS高程擬合依賴于已知點平面位置數據，而沒有考慮到高程異常值與地面高低起伏之間的關系。本文在進行高程擬合時不僅考慮了高程異常與平面的位置間的關系，而且還考慮了與地面的起伏高差之間的關系，在傳統二次曲面GPS高程擬合的基礎上，通過增加一個相對大地高擬合變量，提出了基于相對正常高高程異常的GPS擬合方法，并通過某山區工程實例驗證了此方法的可行性，同時也驗證了采用此方法的擬合精度比傳統二次曲面的GPS高程擬合精度要高。

[1] 張正祿，鄧勇，羅長林，等.利用GPS精化區域似大地水準面[J].大地測量與地球動力學，2006，26(4)：14-17.

[2] 張小紅，程世來，許曉東.基于Kriging統計的GPS高程擬合方法研究[J].大地測量與地球動力學，2007，27(2)：47-51.

[3] 楊江波，李為樂，余代俊，等.GPS高程擬合方法的實驗研究[J].測繪科學，2009，34(3)：54-57.

[4] 黃祥雄，廖超明，曾教勝，等.區域精化似大地水準面在工程三維GPS控制網建設中的應用研究[J].測繪通報，2010(2)：35-37.

[5] 楊明清，靳蕃，朱達成，等.用神經網絡方法轉換GPS高程[J].測繪學報，1999，28(4)：301-307.

[6] 劉俊領，劉海生，王衍靈，等.GPS高程擬合方法研究[J].測繪與空間地理信息，2009，32(1)：143-147.

[7] 魏立峰，何建國.GPS高程擬合似大地水準面的方法[J].地理空間信息，2010，8(4)：72-73.

[8] 李秀海.平坦地區GPS高程擬合方法精度分析[J].黑龍江工程學院學報：自然科學版，2009，23(4)：4-6.

[9] 陳本富，王貴武，沈慧，等.基于Matlab的數據處理方法在GPS高程擬合中的應用[J].昆明理工大學學報：理工版，2009，34(5)：1-4.

[10] 高寧，高彩云，吳良才.GPS高程迭加擬合模型的研究[J].西安科技大學學報，2009，29(3)：339-343.

[11] 吳曉平.似大地水準面的定義及在空中測量中涉及的問題[J].測繪科學，2006，31(6)：24-25.

Discussion on the Relative Height Anomaly of GPS Elevation Fitting Method

CHEN Yanhong，MA Quanming，LIU Ruimin，MAO Xiaokang

P228.4

B

0494-0911(2014)12-0067-03

陳艷紅，馬全明，劉瑞敏，等.基于相對高程異常的GPS高程擬合方法探討[J].測繪通報，2014(12)：67-69.

10.13474/j.cnki.11-2246.2014.0400

2014-01-08

陳艷紅(1977—)，女，河北阜城人，碩士，講師，主要從事大地測量數據處理的研究與工作。