矩陣空間上正線性映射的一個(gè)不等式
劉建忠
(江蘇理工學(xué)院 數(shù)理學(xué)院,江蘇 常州 213001)
0 引言
矩陣及算子不等式理論在自然科學(xué)、工程技術(shù)及社會(huì)科學(xué)各領(lǐng)域具有廣泛應(yīng)用,通過對(duì)矩陣不等式的研究,可以深刻揭示數(shù)量之間的內(nèi)在關(guān)系,而且其理論本身富有技巧性和創(chuàng)造性,在學(xué)術(shù)上是深刻有趣的.由于研究方法靈活多樣,應(yīng)用背景涉及眾多學(xué)科領(lǐng)域,有關(guān)矩陣不等式的結(jié)果散見在各種刊物和著作中,近年來(lái)的一種趨勢(shì)是利用一些一般的理論模式給出各種矩陣不等式的統(tǒng)一形式,例如通過控制不等式理論統(tǒng)一研究有關(guān)矩陣特征值、奇異值及酉不變范數(shù)的不等式[1],利用矩陣空間上線性映射的理論統(tǒng)一處理有關(guān)矩陣二次型、跡、行列式、積和式等不等式[1-2]。
本文利用矩陣張量積的一些基本性質(zhì)及矩陣分塊技巧,得到了矩陣空間上正線性映射的一個(gè)不等式.在所得結(jié)果的基礎(chǔ)上,通過選取適當(dāng)?shù)妮o助函數(shù),可統(tǒng)一導(dǎo)出一些經(jīng)典的矩陣不等式,并可在此基礎(chǔ)上得到一些新的矩陣不等式.有關(guān)結(jié)論容易推廣到Hilbert空間上緊算子所構(gòu)成的空間上,為避免細(xì)節(jié)上的繁瑣,本文的論證僅在矩陣空間上展開。
1 記號(hào)及引理
Mn表示n階復(fù)方陣所成的線性空間,對(duì)于A∈Mn,A>0,A≥0分別表示A為正定、半正定Herimitian陣,A*表示A的共軛轉(zhuǎn)置,σ(A)表示A的譜,即A的特征值所成的集合。若映射Φ:Mn→Mk滿足:
(i)Φ(A+B)=Φ(A)+Φ(B),A,B∈Mn;
(ii)Φ(c A)=cΦ(A),A∈Mn,c為復(fù)數(shù);
(iii)當(dāng)A≥0時(shí),Φ(A)≥0。
則稱Φ為Mn上的正線性映射;若進(jìn)一步滿足當(dāng)A>0時(shí),Φ(A)>0,則稱Φ為Mn上的嚴(yán)格正線性映射;若Φ(In)=Ik,其中In為n階單位矩陣,則稱其為Mn上的單位映射。
引理1[2]設(shè)A,B均為正定陣,則分塊矩陣的充要條件是A≥XB-1X*。
引理2[3]設(shè) A≥0,B≥0,則 A?B≥0。
引理3[2]設(shè)H為Herimitian陣,且分塊矩陣,Φ為正線性映射,則0。
2 主要結(jié)論
定理1 設(shè)A為n階Herimitian陣且 σ(A)?[m,M],f,g,h為[m,M]上的實(shí)值函數(shù)且當(dāng) λ∈[m,M]時(shí) f(λ)≥0,g(λ)≥0,f(λ)g(λ)≥h2(λ),Φ為Mn上的正線性映射且 Φ(f(A))>0,Φ(g(A))>0,則有 Φ(f(A))≥Φ(h(A))Φ-1(g(A))Φ(h(A))。
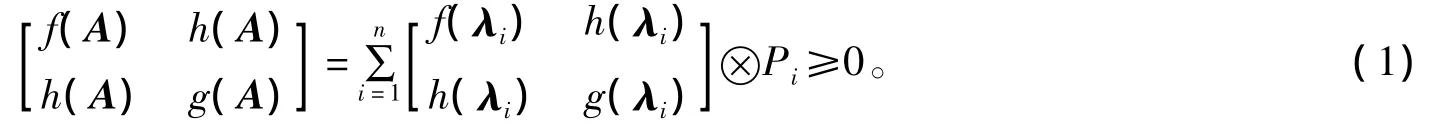
由引理3及(1)得
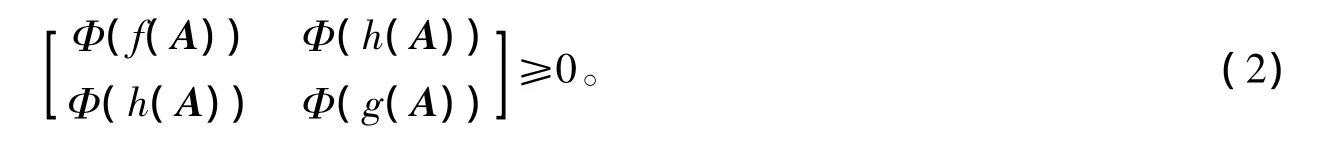
由引理1及(2)即得結(jié)論。
通過選取適當(dāng)?shù)暮瘮?shù)f,g,g,由定理1可得到一些經(jīng)典的矩陣不等式,例如分別選取f(λ)=λ2,g(λ),由定理1經(jīng)直接驗(yàn)算可得
推論1(Kadison's不等式)設(shè)Φ:Mn→Mk為單位正線性映射,則對(duì)任意的Herimitian矩陣A,
Φ2(A)≥Φ(A2)。
推論2(Choi's不等式)設(shè)Φ:Mn→Mk為單位正線性映射,則對(duì)任意的正定矩陣A,
Φ-1(A)≤Φ(A-1)。
當(dāng)k=1時(shí),稱Φ為Mn上的線性泛函,下面我們借助于定理1給出矩陣空間上正線性泛函的一個(gè)新的矩陣不等式。
定理2 設(shè) Φ為Mn上的正線性泛函,A為正定陣,α1,α2,…,αm∈R,則有
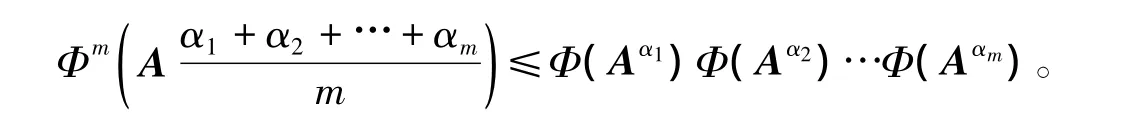
證明 不妨設(shè)Φ為嚴(yán)格正線性泛函,取一組參數(shù)c1,c2,…,cm∈R+,使得c1c2…cm=1,由算術(shù)-幾何平均不等式得
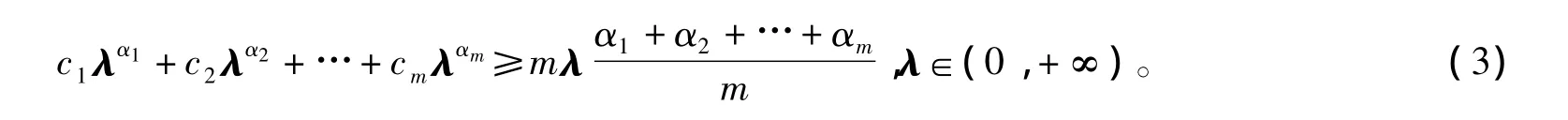
Φ(f(A))≥Φ(h(A))Φ-1(g(A))Φ(h(A)),即
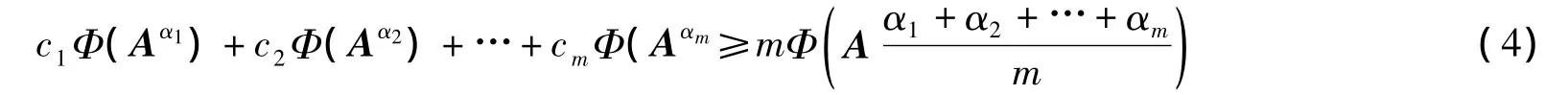
在定理2中分別取Φ(A)=x*A x,tr(AX),其中x∈Cn,X為正定矩陣,可得
推論 3[4]設(shè) A為n 階正定 Herimitian 陣,x為n 維列向量,α1,α2,…,αm∈ R,則 有推論4 設(shè) A,X為n階正定 Herimitian陣,α1,α1,…,αm∈R,則有(Aα1X)tr(Aα2X)…tr(AαmX)。
[1]Rajendra B.Matrix analysis[M].New York:Springer- Verlag,1997.
[2]Rajendra B.Positive Definite Matrices[M].Princeton:Princeton University Press,2007.
[3]詹興致.矩陣論[M].北京:高等教育出版社,2008.
[4]劉建忠.Cauchy不等式和 Kantorovich不等式的推廣[J].河北大學(xué)學(xué)報(bào):自然科學(xué)版,2004,24(3):240-242.

