基于全加速度計慣性測量單元的微震顫測量技術研究

潘鴻飛， 呂雋， 代海洋

（1.92941部隊92分隊，遼寧葫蘆島125001；2.哈爾濱工程大學機電工程學院，哈爾濱150001）

基于全加速度計慣性測量單元的微震顫測量技術研究

潘鴻飛1， 呂雋1， 代海洋2

（1.92941部隊92分隊，遼寧葫蘆島125001；2.哈爾濱工程大學機電工程學院，哈爾濱150001）

對基于全加速度計慣性測量單元的微震顫測量技術進行研究和分析，設計了測量系統的方案并研制了實驗樣機，慣性測量單元采用9加速度計的配置形式；推導了加速度計輸出的比力方程，提出了將積分法和開方法結合起來求解角速度的算法；給出了利用四元數求解捷聯矩陣的數值求解方法和在慣性坐標系下載體系上任意位置在任意時刻坐標的數值求解方法。

微震顫；加速度計；慣性測量單元

0 引言

生理性微震顫是人與生俱來的運動時固有的一種肢體小幅度振動，一般情況下生理性微震顫對人們的影響非常小，但是在某些需要精確操作的場合，如人在回路的導彈攻擊操作等，生理性微震顫的影響是不能忽視的［1-2］，必須考慮由生理性微震顫給操作所帶來的不精確性和不穩定性。另外，隨著智能電子設備的普及，人在回路的導彈攻擊操作，生理性微震顫對于攝像機、瞄準系統和手寫設備輸入的影響也同樣不容忽視。因此，開發簡單、易用、廉價的震顫抑制系統有著較強的現實意義。

1 微震顫測量單元的方案設計

圖1 震顫測量加速度計安裝示意圖

圖2 震顫測量單元的試驗樣機

本文設計的震顫測量單元采用3個雙軸加速度計和一個三軸加速度計構成的全加速度計慣性測量系統，加速度計的安裝示意圖如圖1所示，3個雙軸加速度計安裝在彼此相鄰的立方體的面中心處，三軸加速度計的中心位于立方體的中心，這種配置方式在角速度的解算算法中，充分利用了9加速度計配置方案輸出的冗余信息，角速度的大小由開方得到，角速度的方向通過判斷角加速度的大小來確定，避免了由積分求取角速度所帶來的累積誤差［3］。加速度計選擇ADXL203雙軸加速度計和KXR94-2283三軸加速度計，震顫測量單元的試驗樣機如圖2所示。

2 加速度計輸出的比力方程

設｛b｝為載體坐標系，｛i｝為慣性坐標系，載體坐標系以載體質心為坐標原點，慣性坐標系以地面選定的參考點作為坐標原點，其中載體坐標系的坐標軸方向與放置在載體系質心的三軸加速度計的敏感軸同向，如圖1所示。初始時刻，載體系與慣性系重合。

設載體上任一點在載體坐標系中用矢徑r表示，在慣性坐標系中用矢徑R′表示，載體坐標系原點在慣性坐標系中用矢徑R表示，r、R、R′之間的相互關系如圖3所示，有：

由哥氏定理，對式（1）求導：

式中ωib為載體系在慣性系中轉動的角速度。

圖3 坐標系間轉換示意圖

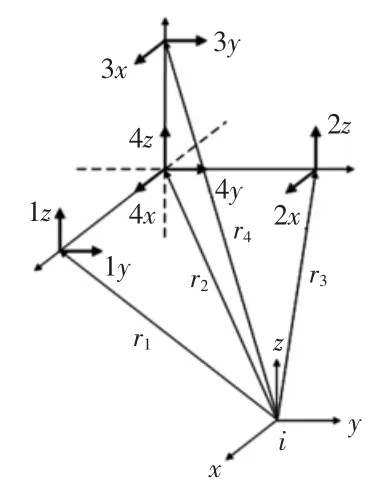
圖4 加速度的敏感軸編號及位置示意

式中：Ai為載體質心處的比力；Gi為地球引力加速度；fi為載體系上任一點處的比力。

結合式（3）、式（4）、式（5），載體上任一點處的比力為：

對圖4中加速度計各個敏感軸應用比力方程，有：

式中：fij為編號為i的加速度計在敏感軸j方向上測量的比力；Aij為編號為i的加速度計在慣性坐標系j方向的加速度；ribj為編號為i的加速度計矢徑在載體坐標系j方向上的投影；ωij為載體系的角速度在慣性系j方向上的分量。

在圖4中，由加速度計之間的相對位置關系可以得到：

式中：l為加速度計敏感軸中心與載體系坐標原點之間的距離。

在理論上，在方向j上，Aij是相同的。由式（7）和式（8），對敏感軸同向的比力方程進行運算，消除加速度的平方項，帶入相應的值，可以得到：

對式（9）進行變換，分別得到角速度的平方、微分和交叉乘積：

在本文設計的震顫測量系統中，加速度的測量存在較多的冗余信息，載體系每一個方向上的加速度均有3個測量值，為了全面利用測量信息，提高測量精度，設載體在3個方向上的加速度用式（11）表示：

式中：ki為編號為i的加速度計測量值的可信度；σAij為編號為i的加速度計j敏感軸方向上測量值的標準差；

可信度ki的計算涉及到安裝誤差及其它因素，由于3個雙軸加速度計為同一型號，ki近似取為1/3。

從式（10）可以看出，角速度的求解可以采用積分和開方兩種方式，其中開方可以直接對角速度平方項取平方根，也可以對相鄰兩軸角速度的乘積項做代數運算，然后取平方根。利用積分法求解角速度會出現累積誤差，盡管所使用的加速度計精度較高，但加速度計的零漂不穩定，所引入的誤差會隨著積分而不斷累積，且由此帶來的誤差沒有邊界；利用開方求解角速度時，雖然不會帶來累計誤差，但是角速度的符號無法直接由計算得到，需要通過其它輔助手段確定。將積分法和開方法結合起來求解角速度，可以在一定程度上避免單獨使用開方法或積分法求解角速度所帶來的問題。從文獻［4］和［5］中可知，在積分法求解角速度的過程中，其主要誤差來源于加速度計輸出的零漂。零漂屬于隨機誤差，盡管可以通過硬件在試驗前進行調整，但加速度計的零漂并不能完全消除。從所選擇的加速度計的手冊和所確定的輸出帶寬可以得到兩種加速度計所引入的噪聲的有效值分別為

圖5 積分法和開方法角速度解算誤差仿真結果

3 捷聯矩陣即時修正算法

在震顫測量中，采用捷聯矩陣將載體系下的加速度和角速度轉變為慣性系下的絕對加速度和角速度，測定載體的姿態。設捷聯矩陣為T，則載體系與慣性系之間的

在測量過程中，需要不斷地對捷聯矩陣T進行修正，修正算法很多，主要有方向余弦算法、歐拉角變換算法和四元數算法等［6］。本文采用四元數算法，便于數值積分求解。

四元數由一個實數和三個虛數構成，表達式［7］為

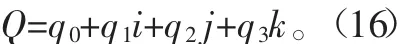
由歐拉定理可知，具有固定點的剛體，其位置的變化可以通過剛體繞通過固定點的旋轉軸轉過一定的角度得到。

圖6 歐拉定理示意圖

設剛體繞旋轉軸轉過θ角，軸線在參考系中的方向余弦分別為cosα、cosβ、cosγ，則轉軸的方向可以表示為：

該轉動用四元數表示為：

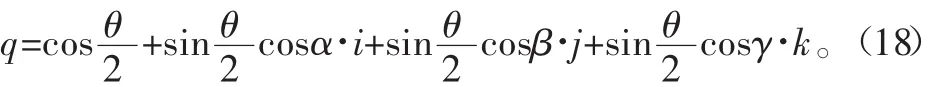
從四元數的表示形式中可以看出，四元數既包含了轉軸的方向，也包含了轉角的大小。捷聯矩陣的四元數表示形式為［7］

對式（19），只要知道了四元數中的4個元，即可求出捷聯矩陣。載體坐標系時刻都在變化，因此，捷聯矩陣也在時刻變化。捷聯矩陣中四元數與角速度的關系為如下

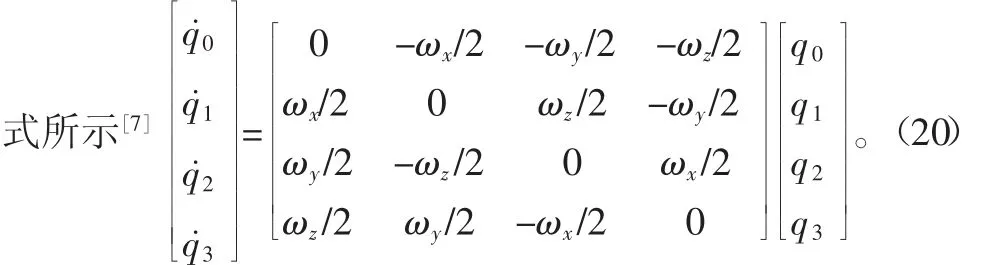
由式（10）可以求出ωx、ωy、ωz，從而得到關于四元數的微分方程組。

用式（19）來簡寫式（18）。關于式（19）所表示的微分方程組，利用四階龍格——庫塔進行數值求解，迭代過程為：

在使用式（20）進行迭代的過程中，需要初始時刻的值。根據坐標系的定義，參數的初始值為

根據四元數的定義，有：

結合式（20）和實時求解的角速度，即可實時計算出捷聯矩陣，求出載體系下的物理量在載體系下的表示。

4 載體絕對位置的求解

根據捷聯矩陣，加速度在慣性系中表示為

載體系上任一點任一時刻在慣性系中相對于載體系原點可以表示為

式中：ri為載體系上一點在慣性系中的矢量；rb為載體系上一點在載體系中的矢量。

載體系上任一點在任一時刻的位置可以表示為

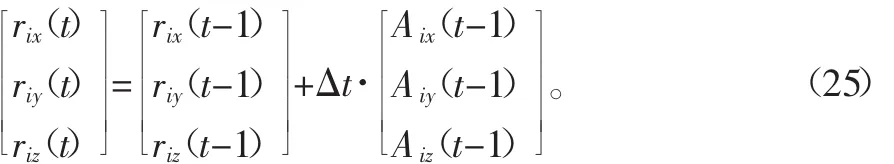
5 結論

本文對生理性微震顫及其對精確操作的影響進行研究和分析，對基于慣性測量原理的生理性微震顫測試技術進行研究；設計了基于全加速度計慣性測量單元的生理性微震顫測量方案并研制了實驗樣機，慣性測量單元采用9加速度計的配置方式，避免了求解微分方程組；角速度的解算采用積分——開方融合算法，解決了積分法求解角速度時誤差累計的問題，提高了測量的精度；用來實現物理量坐標系轉換的捷聯矩陣的求解采用四元數方法，這種方法易于在實時系統上實現。

［1］ Win T L，Tan U X，Shee C Y，et al.Design and Calibration of an Optical Micro Motion Sensing System for Micromanipulation Tasks［C］//IEEE International Conference on Robotics and Automation，Roma，Italy，2007:3383-3388.

［2］ Ang W T，Riviere C N，Khosla P K.Design and Implementation ofActive ErrorCanceling in Hand-held Microsurgical Instrument［C］//International Conference on Intelligent Robots and Systems，Maui，USA，2001：1106-1111.

［3］ 王勁松，王祁，孫圣和.無陀螺微慣性測量組合的優化算法研究［J］.哈爾濱工業大學學報，2002，34（5）：632-635.

［4］ 趙國榮，陳穆清.一種用于九角速度計GFSINS的姿態角速度輔助算法［J］.系統仿真學報，2007，19（14）：3350-3353.

［5］ 劉濤，趙國榮，潘爽.無陀螺捷聯慣導系統角速度解算的新方法［J］.系統工程與電子技術，2010，32（1）：162－165.

［6］ 陳哲.捷聯慣導系統原理［M］.北京：宇航出版社，1986：885.

［7］ 朱家海.慣性導航［M］.北京：國防工業出版社，2008：209-213.

［8］ Rocon E，Ruiz A F，Pons J L.Rehabilitation Robotics：a Wearable Exo-skeleton for Tremor Assessment and Suppression［C］// IEEE International Conference on Robotics and Automation，Barcelona，Spain，2005：2271-2272.

［9］ 柳迪.消除手術機器人人手抖動問題的研究［D］.天津：天津大學，2009.

［10］ Latt W T，Tan U X，Shee C Y，et al.Ang.A Compact Handheld Active Physiological Tremor Compensation Instrument［C］//International Conference on Advanced Intelligent MechatronicsSuntecConvention and Exhibition Center，Singapore，2009：711-716.

（編輯：啟 迪）

Research of Micro-tremble Measuring Technique Based on Total Accelerometer Inertial Measurement Unit

PAN Hongfei1,LV Jun1,DAI Haiyang2
（1.CPLA 92941 Unit 92 Element,Huludao 125001,China；2.College of Mechanical and Electrical Engineering, Harbin Engineering University,Harbin 150001,China）

Micro-tremble measuring technique based on total accelerometer inertial measurement unit is researched and analyzed.Measurement unit is designed and experimental model machine is developed.Inertial measurement unit consists of nine accelerometers.This paper derives specific gravity equation of accelerometer and forwards an algorithm combined of intergration and extraction of root to solve angular velocity.Computation method using quaternion computation of srrapdown matrix and computation method of arbitrary position at arbitrary time in inertial reference system are given.

micro-tremble;total accelerometer;inertial measurement unit

TB 114.3

A

1002－2333（2014）04－0044－04

潘鴻飛（1971—），男，碩士研究生，研究方向為導彈武器裝備試驗與鑒定。

2014-02-11