關于定積分元素分析法的一種新理解
侯國亮
(長春師范大學數學學院,吉林長春 130032)
關于定積分元素分析法的一種新理解
侯國亮
(長春師范大學數學學院,吉林長春 130032)
本文通過引入線矩形、線扇形和面圓柱體等微分概念,給出了對定積分元素分析法更本質、更通俗的理解,突破了“定積分在幾何學上的應用”這一教學難點。
線矩形;線扇形;面圓柱體;元素分析法;定積分
在眾多《高等數學》教材中有關定積分應用知識的介紹,通常是先采用元素分析法把要解決的實際問題抽象成一個具體函數的定積分,然后再用計算定積分的相關知識進行求解,其中元素分析法是定積分應用教學的重點,元素分析法是教學的難點:一是教師理解但表述不清,講不徹底,總感覺元素分析法是只可意會不可言傳的一個知識點;二是學生不理解,覺得不可思議.針對這一情況,筆者進行了教學改進,從學生反饋回來的信息來看,可以取得較好的教學效果.
首先給出幾個常用的公理和定理.
公理1 點構成線,線構成面,面構成體.
定理1 單獨一個點的長度為零,構成線(段)的點的長度不為零.
定理2 單獨一條線(段)的面積為零,構成平面(區域)的線(段)的面積不為零.
定理3 單獨一個平面(區域)的體積為零,構成體的平面(區域)的體積不為零.
事實上,定理1、定理2、定理3的正確性是很顯然的,比如定理2,假如構成一個具體平面圖形的線段的面積為零,那么該平面圖形的面積也應該為零,這顯然是不可能的事情.
1 求平面直角坐標系中不規則圖形的面積
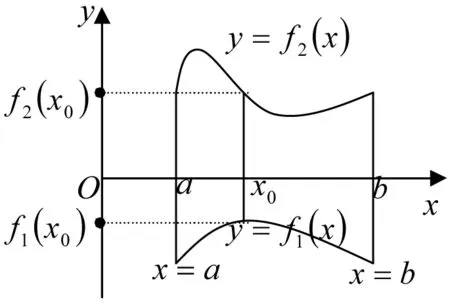
圖1 曲邊梯形1
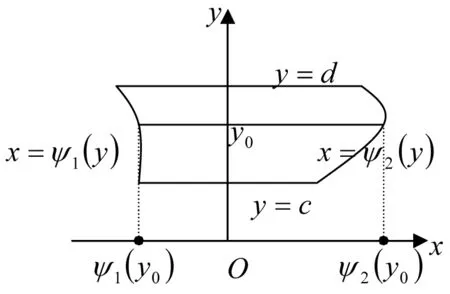
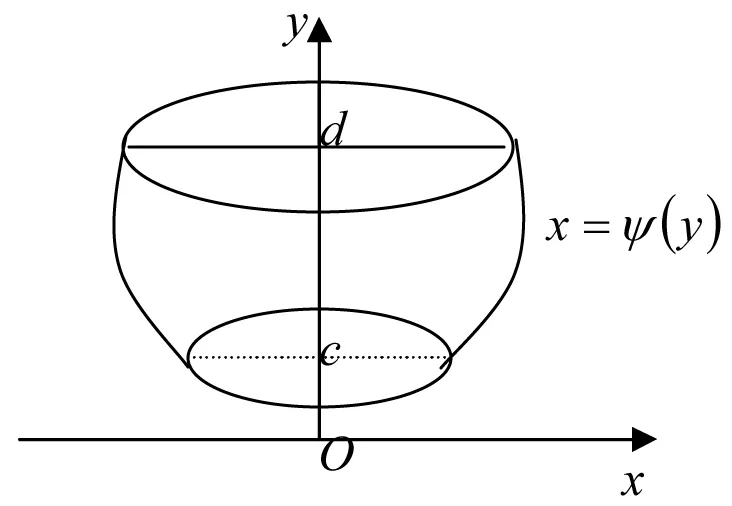
已知由曲線y=f1(x)、y=f2(x)及直線x=a,x=b(a 對于這個公式的得出,也即對元素分析法的理解,在課堂上可以這樣闡述:依據公理1,把該圖形看成是由區間[a,b]上垂直于x軸介于曲線y=f2(x)與y=f1(x)之間的所有線段構成,那么根據定理2,該平面圖形的面積就應該等于這些線段的面積之和. 當然,也可以把該圖形看成是由其他形式的無數多條線段構成,但在選擇圖形是由哪些具體線段構成時需要注意兩點:一是構成圖形的線段不能重復也不能遺漏,否則,這些線段的面積和就不等于圖形的面積;二是構成圖形的所有線段的面積要能用同一個變量的微分關系式表出,比如,區間[a,b]上垂直于x軸介于曲線y=f2(x)與y=f1(x)之間的所有線段的面積都可以用[f2(x0)-f1(x0)]dx,x0∈[a,b]表示,所以通常情況是把平面直角坐標系里的圖形看成是由某指定區間上垂直于x軸,或y軸的線段構成. 圖2 曲邊梯形2 對于后一種情形,可參考如下例子:已知由曲線x=ψ1(y)、x=ψ2(y)及直線y=c,y=d(c 最后,需要指出的是,把一個平面圖形看成是由垂直于軸還是軸的線段構成的關鍵取決于所給圖形的具體形狀,若是圖1所示的形狀,則選擇垂直于x軸;若是圖2所示的形狀,則選擇垂直于y軸. 如果一個圖形既可以看成是圖1所示的形狀,又可以看成是圖2所示的形狀,則以計算方便為選擇準則. 圖3 曲邊扇形 設由曲線ρ=φ(θ)及射線θ=α,θ=β(α<β)圍成一圖形,稱之為曲邊扇形(圖3),其中φ(θ)在[α,β]上連續,且φ(θ)≥0. 現在要計算它的面積. 首先,仿照問題1中線矩形的定義,給出線扇形的定義及面積計算公式. 定義1 把扇形當圓心角趨向于零時的極限形式稱為線扇形. 圖4 旋轉體1 旋轉體是由一個平面圖形繞這平面內一條直線旋轉一周而成的立體.這直線叫做旋轉軸. 例如,圓柱、圓錐、圓臺、球體可以分別看成是由矩形繞它的一條邊、直角三角形繞它的直角邊、直角梯形繞它的直角腰、半圓繞它的直徑旋轉一周而成的立體. 所以它們都是旋轉體. 圖5 旋轉體2 根據公理1,可以把該立體看成是由區間[a,b]上垂直于x軸、以函數值f(x0),x0∈[a,b]為半徑的所有圓平面構成,再由定理3可得其體積等于這些圓平面的體積和,因為這時的圓平面是圓柱體當高度趨向于零時的極限形式,所以這些圓平面的體積應該按照圓柱體的體積計算公式來進行計算,即為底面積乘高,所以位于點處的圓平面(圖4)的體積為π[f(x0)]2dx,其中dx為它的高,進而可得該旋轉體的體積為π[f(x0)]2dx. 另外,為了以后敘述的方便,把這些構成旋轉體的圓平面稱之為面圓柱體. 基于定積分的元素分析法所作的上述解釋具有普遍實用性,任意一個確定的立體,都可以看成是該立體上垂直于一定軸的一組截平面構成,由于構成該立體的這組截平面不一定是圓形,所以對應于不同的情況,就會有不同的稱呼,比如面橢圓柱體、面三棱柱體等. [1]同濟大學數學系.高等數學(上冊)[M].6版.北京:高等教育出版社,2007:223. A New Way to Comprehend the Element Analysis Method of Definite Integral HOU Guo-liang (School of Mathematics, Changchun Normal University, Changchun Jilin 130032, China) In this paper, we offer a more natural and popular way to comprehend the element analysis method of definite integral by defining some differential concepts, such as linear rectangle, linear sector, plane cylinder and so on, so that we make a breakthrough on teaching difficulty about the application of definite integral to geometry. linear rectangle;linear sector;plane cylinder;element analysis method;definite integral 2014-05-08 侯國亮(1981- ),男,河南安陽人,長春師范大學數學學院講師,碩士,從事基礎數學研究。 O172.2 A 2095-7602(2014)04-0017-03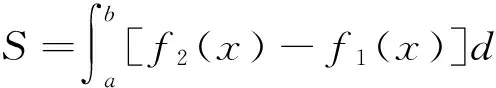
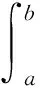
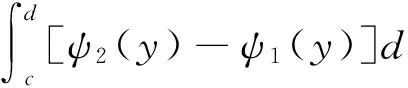
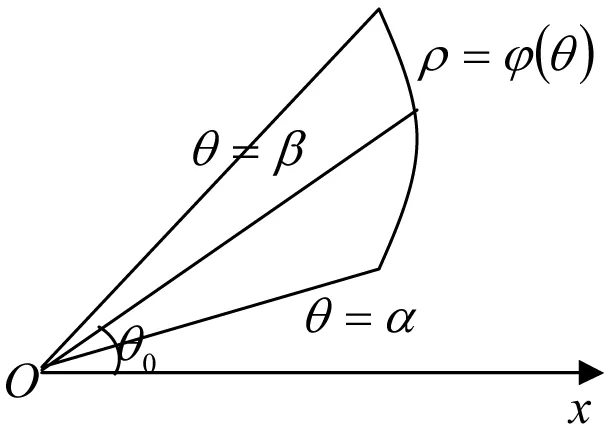
2 求平面極坐標系中不規則圖形的面積

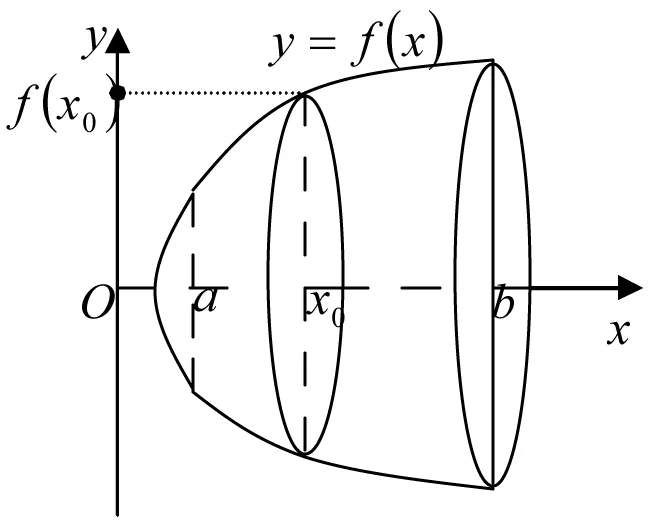
3 求三維直角坐標系中旋轉體的體積

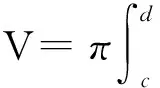
4 結語

