擴展的F-展開法在耦合KdV方程精確解中的應用

于 義

(撫順師范高等專科學校，遼寧撫順 113001)

擴展的F-展開法在耦合KdV方程精確解中的應用

于 義

(撫順師范高等專科學校，遼寧撫順 113001)

本文以數學機械化思想為指導，以計算機代數系統軟件Maple為工具，提出了用擴展的F-展法來構造非線性孤子方程的行波解。為了驗證方法的有效性和優越性，將其應用到耦合的KdV方程，獲得了具有一般形式的新的精確解，其中包括單的和耦合的Jacobi橢圓函數解、類孤子解及三角函數解。

孤子方程；精確解；F-展開法

一般來說，計算分為兩大類：一是數值計算；二是符號計算.數值計算對人們來說是比較熟悉的，并且比符號計算發展得迅速.隨著計算機及符號軟件的產生，如Maple，Mathematica等，符號計算已成為現代數學研究中非常重要的工具，并且已滲透到其他很多領域[1-3].我國著名數學家、中國科學院院士吳文俊先生在對中國古代數學思想研究的基礎上發展并完善了Ritt的方法，于1978年創立了吳代數消元法，將該方法用于初等幾何的機械化證明，獲得了很好的結果.在吳文俊院士的大力倡導下，數學機械化思想得到了迅速的發展，已滲透到了諸多領域，如理論物理、CAD、CAGD、機器人及控制論、力學和組合學等.數學機械化連續列為“八五”、“九五”國家攀登計劃及“973”目之一.為了更準確地研究物體變化的性質，我們需要尋求其對應方程的精確解.

1 擴展的 F-展開法

F-展開法[4-5]是用雅克比橢圓函數展開方法求非線性數學物理方程周期波解的方法，即把方程的解表示成雅克比橢圓函數冪次展開的形式.用它得到了很多非線性偏微分方程的周期波解.下面給出F-展開法的一個推廣.

對給定兩個自變量的非線性偏微分方程

P(u,ut,ux,utt,uxt,…)=0.

(1)

其中P是一個多項式，它含有非線性項和線性出現的高階偏導數項.我們分以下五個步驟求其橢圓函數周期波解：

第一步，對方程(1)作行波變換u(x,t)=u(ξ)，ξ=kx+ωt+k0，其中k,ω是待定常數，k0是任意常數，則(1)式化為：

P(u,ωu′,ku′,ω2u″,ωku″,k2u″,…)=0.

(2)

第二步：設u(ξ)可表示為F(ξ)的有限冪級數

(3)

這里a0,a1,a2，…,aN為待定常數.N為非負整數，將由非線性項和最高階偏導數項的齊次平衡來決定.F(ξ)是雅克比橢圓函數滿足Riccati方程：

F′2(ξ)=PF4(ξ)+QF2(ξ)+R.

(4)

F"(ξ)=2PF3(ξ)+QF(ξ).

(5)

F?(ξ)=(6PF2(ξ)+Q)F′(ξ).

(6)

其中P,Q,R,F(ξ)有如下的關系：

第三步：將(3)代入(2)，利用(4)(5)(6)將(2)左端變為F(ξ)的多項式，再令其各次幕的系數為0，得a0,a1,a2，…，aN,ω(或k)的代數方程組.

第四步：解該方程組，將a0,a1,a2，…，aN,ω(或k)用P，Q，R來表示.將它們代入(3)式，得我們所解方程的一個行波解的一般形式.

第五步：選取(P，Q，R)使F(ξ)是某一種雅克比橢圓函數.將選定的(P,Q,R)的值和相應的雅克比橢圓函數代入方程行波解的一般形式中，可得方程的各種用雅克比橢圓函數表示的周期波解.

2 應用

下面以耦合KdV方程

(7)

為例，利用擴展F-展開法求其精確解.

首先對耦合KdV方程做行波變化u=u1(ξ),v=v1(ξ)，ξ=kx+ωt+k0，其中k0為常數，k,ω待定.

(8)

(9)

令

(10)

(11)

其中ai,bi,ci,di,ei,fi,gi,hi均為常數.將(4)(5)(6)代入(10)(11)，并利用符號計算軟件Maple選擇關于F'iFj的系數，并分別令其為零得到下面的代數超定方程(由于方程較多，這里將其省略).進一步，解上述代數方程得如下三種情形非平凡解：

情形1：a0=a0,k=k,e0=e0,a1=0,b1=0,b2=0,c1=0,c2=0,d1=0,d2=0,e1=0,e2=0,f1=0,f2=0,g1=0,g2=0,h1=0,h2=0,a2=-2k2P1,ω=-4k3Q1-6ka0,

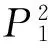
情形3：k=k,e1=e1,e2=0,g2=0,d2=0,c2=0,b2=0,a1=0,h1=0,h2=0,

c1=0,d1=0,g1=0,f1=0,e0=0,f2=0,

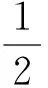
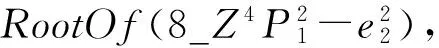
由于篇幅有限，下面僅對對于情形3，給出耦合KdV的一些精確解.

(i)P1=m2,Q1=-(1+m2),Q1=-(1+m2),F(ξ)=snξ,

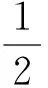
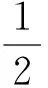
代入(10)(11)得方程的一組解

其中a0,e0,k為任意常數.

黨的十八屆三中全會提出了健全軍隊院校教育、部隊訓練實踐、軍事職業教育“三位一體”的新型軍事人才培養體系。在“三位一體”軍事人才培養體系中，把軍隊院校教育、軍事職業教育并列。其中，軍隊人員離崗進校接受教育培訓就是軍隊院校教育，在崗接受教育培養就是軍事職業教育。因此，軍事職業教育本質上屬于在崗繼續教育，只是面向的對象是軍隊人員。軍事職業教育已經進入了黨的十八屆三中全會決定，進入了中央軍委決策。軍事職業教育，應以改善學員知識結構、提升武器裝備運用能力、增強全面綜合素質為目標，科學構建完善的軍事職業教育課程體系，應從修訂軍事職業教育的課程標準、調整教學內容、創新課程教學手段與方法入手。

當m→0時，snξ→sinξ，因此有

當m→1時，snξ→tanhξ，因此有

其中a0,e0,k為任意常數.

(ii)P1=-m2,Q1=2m2-1,F(ξ)=cnξ,

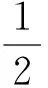
代入(19)(20)得方程的一組解

其中a0,e0,k為任意常數.

當m→0時，cnξ→cosξ，因此有

當m→1時，cnξ→sechξ，因此有

其中a0,e0,k為任意常數.

(iii)P1=1,Q1=-(1+m2),F(ξ)=nsξ,

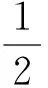
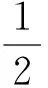
其中a0,e0,k為任意常數.

當m→0時，ns→cscξ，因此有

當m→1時，nsξ→cothξ，因此有

其中a0,e0,k為任意常數.

[1]朝魯.吳-微分特征列集法理論極其在微分方程對稱和力學中的應用[D].大連:大連理工大學,1997.

[2]Wang ML,Wang MY,Zhang JL.The periodic wave solutions for two systems of nonlinear wave equations[J]. Chin. Phys,2003(12):1341-1348.

[3]Fan EnGui.Extended tanh-function method and its applications to nonlinear equations[J].Phys Lett A,2000(277):212-218.

[4]Wang ML,Li XZ.Applictions of F-expansion to periodic wave solutions for a new Hamiltonian amplitude equation[J].Chaos Solitons Fractals,2005(24):1257-1268.

[5]Liu JB,Yang KQ.The extended F-expansion method and exact solutions of nonlinear PDEs[J].Chaos Solitons Fractals, 2004(22):111-121.

The Application of Extended F-expansion Method to Exact Solutions of Nonlinear Coupled KdV Equations

YU Yi

(Fushun Teachers College，Fushun Liaoning 113001，China)

The thesis improves the F-expansion method for constructing travelling wave solutions of nonlinear soliton equations under the guidance of mathematics mechanization and with the tools of transformation and computer algebraic system Maple. In order to illustrate the effectiveness and advantages of the method, the study applies it to the coupled KdV equations. Many new and general formal exact solutions for the coupled KdV equations are obtained including the single and combined Jacobi elliptic function solutions, soliton-like solutions, trigonometric function solutions.

Soliton equations;Exact solutions;F-expansion method

2013-11-25

于 義(1962- )，男，遼寧撫順人，撫順師范高等專科學校副教授，從事可積系統研究。

O29

A

1008-178X(2014)01-0014-04