簡諧運動與音樂的聯系及其可視化

徐富清

（揚州市邗江區公道中學 江蘇 揚州 2251 19 ）

兩年前，講完簡諧運動一章后，無意中向學生展示了幾幅李薩如圖形，告訴他們簡諧運動與音樂有深深的聯系，且這里的李薩如圖形是由兩個簡諧運動合成的結果．頓時學生紛紛提出問題，為什么幾個簡諧運動就會合成一個個漂亮的圖形？這種圖形還有哪些表現？音樂怎樣通過簡諧運動表現出來……

事后查閱了大量資料，發現有兩種典型的諧振儀，分別是橫向式諧振儀和轉動式諧振儀，可以將幾個簡諧運動合成李薩如圖形，然后，使用MATLAB工具就可將音樂與李薩如圖形的關系以可視化的方式表現出來．

首先，通過振動了解音樂，了解單擺的頻率與音程之間的關系．

1 泛音與音程

1．1 彈撥琴弦

仔細聆聽，你聽到的不只是基礎音（主調音），還會聽到多重和聲，也就是泛音．如圖1呈現了前5個泛音，藍、綠點是琴弦振動的波節．

圖1

1．2 琴弦上各音程的位置

根據振動的知識，當音的頻率比呈簡單整數關系時，就會產生悅耳的和聲．圖2是一根琴弦上各音程的位置．以“第二音程，五度 ——3∶2”為例，當琴弦振動時，用手按住A點（圖2），A點右側部分的弦長占整個弦長的，那么就形成“第二音程，五度”．

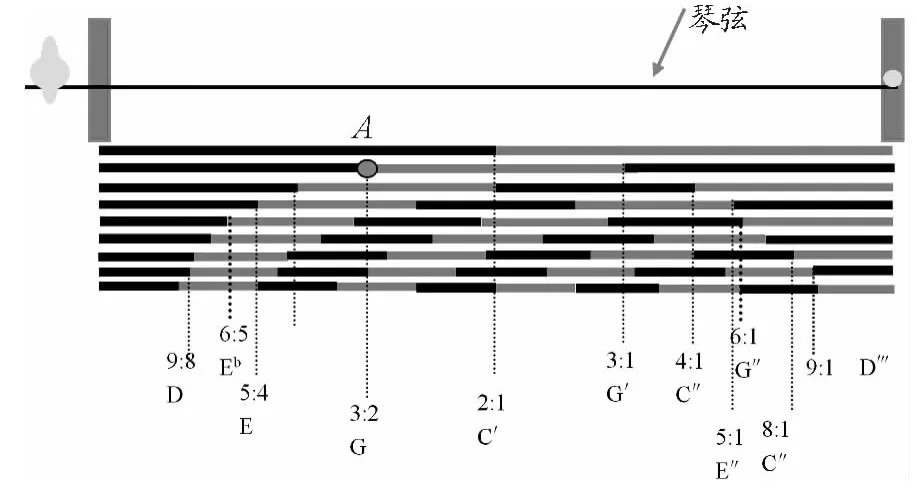
圖2 一根琴弦各音程的位置

2 音程與單擺的頻率

由于不同音樂家演唱的聲音頻率是不同的，但他們每個人在整首曲子中聲音的音階比是不變的，那么，表現樂音的最佳方法就是將樂音的頻率降低10 ～100 倍，這樣，通過單擺的振動，以肉眼就能“看到”音樂了．

簡單的諧振儀使用兩個擺來代表和聲，其中一個擺錘放到最低位置，另一個擺錘的位置則依特定的比率設置．表1給出了單擺的頻率與音程之間的關系．

表1 單擺的頻率與音程的關系

3 兩種諧振儀和MATLAB工具

3．1 橫向式諧振儀

如圖3所示，這種諧振儀有2個擺，分別經由洞孔懸于臺面下方，它們的擺動方向彼此垂直．兩個擺的柄都突出臺面，其中一個擺錘的柄上裝了個平臺，上面夾著一張紙，另一個擺的柄上則裝了一支帶筆的筆桿．

圖3 橫向諧振儀

兩個擺錘擺動時，筆就會描繪出兩者合成運動的結果．剛開始時兩擺長度相等，接著縮短其中一擺的長度，如此就可以依次呈現出各種和聲的頻率比．

3．2 轉動式諧振儀

如圖4所示，這種諧振儀有3個擺，由于兩側的兩個擺的擺動方向彼此垂直且振幅相等，二者的合運動是一個圓周，而中間擺做的是圓周運動，因此三者的合運動是2個圓周運動的結合．

圖4 轉動式諧振儀

3．3 MATLAB工具描述

MATLAB是一款功能非常強大的軟件，在其具有的眾多優點中比較突出的，是以可視化的方式將計算結果快速、準確地用圖形的方式形象、直觀地描繪出來．本文就使用MATLAB軟件將兩個單擺的復合運動以可視化方式表達音樂．

4 簡諧運動與音樂的可視化

4．1 橫向式諧振儀中的音樂可視化

（1）橫向八度 ——2∶1

若一擺的頻率是另一個的2倍，并且兩者的擺動方向呈直角，這時的八度就會繪出數字8的形狀，且相位差不同時得到的結果也不同，如圖5，圖6．如果讓兩擺不斷反復，振幅隨著擺動的減弱而減小，得到的結果如圖7所示．

圖5 相位差是

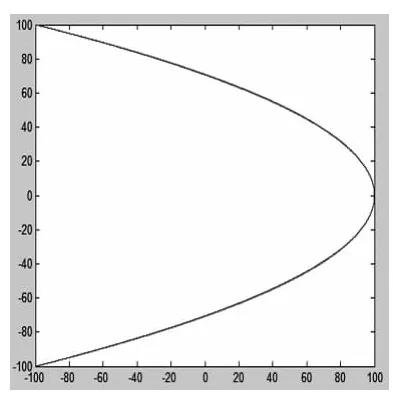
圖6 相位差是

圖7 振幅減小，相位差是

（2）橫向四度 ——4∶3

若兩單擺振動的頻率之比是4∶3，并且兩者的擺動方向呈直角，相位差不同時得到的結果也不同，如圖8～10 所示．

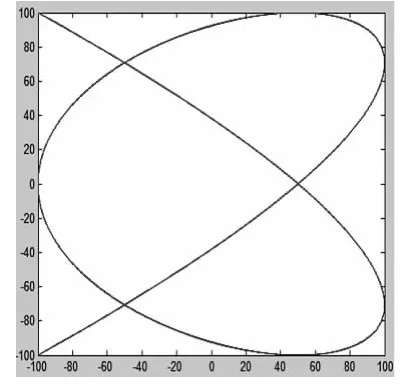
圖8 相位差是

圖9 相位差是

圖10 相位差是

（3）橫向大三度 ——5∶4

若兩單擺振動的頻率之比是5∶4，并且兩者的擺動方向呈直角，相位差不同時得到的結果也不同，如圖11 ～13 所示．

圖11 相位差是

圖12 相位差是

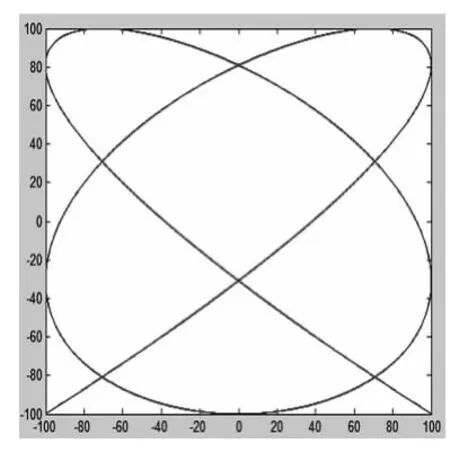
圖13 相位差是

顯然，合成運動的圖形不僅與振動頻率有關，而且相位差不同時，結果也不相同．橫向式諧振儀表現圖形相對簡單、單調．但是轉動式諧振儀表現出的圖形就雅致而令人驚奇．

4．2 轉動式諧振儀中的音樂可視化

（1）旋轉八度 ——2∶1

這時兩擺的運動情形是兩個圓周運動的結合，其中一個擺的速率剛好是另一個的2倍．筆者發現當兩擺振幅相等，且同相位或相位差為π時，分別呈現出心形、三葉草形狀，如圖14 ，15 所示；當兩擺振幅不相等且相位差為π時，呈現為三角形，如圖16 所示．

圖14 心形，同相位

圖15 三葉草，相位差π

圖16 三角形，振幅不相等，相位差π

（2）旋轉五度 ——3∶2

若兩擺圓周運動的速率之比是3∶2，當兩圓周運動振幅相等，相位差為π，不斷反復且振幅隨著擺動的減弱而減小時，呈現出五葉草形，如圖18 所示；兩圓周運動振幅不相等，相位差為π，振幅隨著擺動的減弱而減小時，呈現出五角星，如圖19 所示．

圖17 同相位

圖18 五葉草，振幅減小，相位差是π

圖19 五角星，振幅不相等，相位差是π

（3）旋轉大三度 ——5∶4

若兩擺圓周運動同相位，速率之比分別是5∶4和5∶1，合成運動的結果分別如圖20 和圖22 所示，它們表現出奇異而與眾不同的特質．

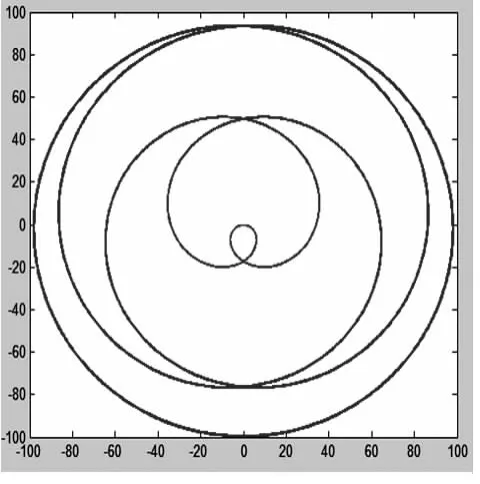
圖20 同相位

圖21 振幅不相等，相位差π

圖22 頻率5∶1，同相位

5 小結

如果將MATLAB程序中的參數略微改變一些，比如，改變簡諧振動的頻率、相位、振幅等，筆者發現很多有趣的圖形，有時令人感到有些不可思議，比如下面2例．

（1）略微改變頻率，產生“拍”的現象．如圖23 所示，這個形狀就是從天王星上觀察到的海王星運行軌跡，這是因為這兩顆行星都是同向繞日運行，天王星的周期為84 年，海王星則為165 年，大致相當于一個八度．

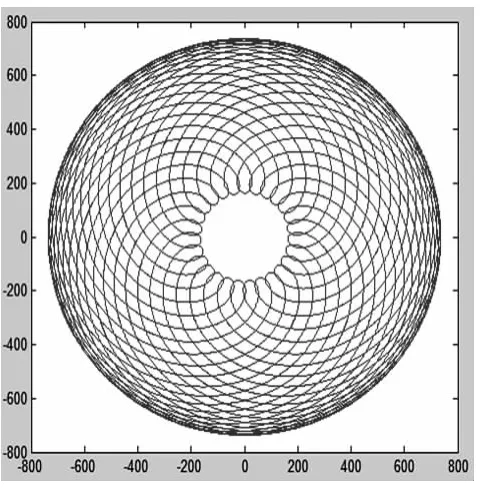
圖23 不同頻率

（2）就旋轉圖形而言，振幅比“相位”更重要，相位僅僅影響到頁面整個構圖的放置方向．如圖24 和圖25 所示，這兩圖都是音階十一度（頻率8∶3），圖24 兩個單擺的振幅是相同的，圖25 兩單擺的振幅是不同的，且在運動過程中它們的振幅逐漸減小．

圖24 振幅相同

圖25 振幅不同

6 結束語

上學期，筆者將所發現的音樂與李薩如圖形之間的關系一一展示給學生欣賞，目的是培養學生的科學素養，激發他們的想象，知道物理學不是單調枯燥的，關鍵是以怎樣的方式表達．這要求教師在教學過程中要以一種超前的戰略眼光，培養學生勇于探索的科學精神，以開放的思維、大膽的設想提出自己的見解．在課堂教學中提倡以一種活潑而靈動的、寓教于樂的方式傳輸知識，某個時候，師生的關系會在某個點上能夠產生“共鳴”．

1 （英）安東尼·艾希頓著．諧振儀——音樂數學原理的可視化向導．賀俊杰譯．長沙：湖南科學技術出版社，2012

2 鐘季康，鮑鴻吉．大學物理習題計算機解法——MATLAB編程應用．北京：機械工業出版社，2008

3 彭芳麟．數學物理方程的MA TA L B解法與可視化．北京：清華大學出版社，2004