磁懸浮平臺中開環磁路的漏磁通分析*

吳國慶，錢小磊，張旭東，孫后全

(1.南通大學 機械工程學院，江蘇 南通226019;2.南通大學 電氣工程學院，江蘇 南通226019)

0 引言

磁懸浮平臺的設計是研究各種磁懸浮加工機床的基礎工作，包含懸浮系統和直線驅動系統，按作用力的方向，分為是垂直系統和水平系統。懸浮系統是一種典型的非線性控制系統［1］，在實際工程中，由于平臺上載荷的變化和加工刀具的切削力引起的振動等不確定因素，使得系統更為復雜。因此實現懸浮系統的精密控制需要建立較為合理的電磁力數學模型。傳統的解決思路是設計工作磁路，等效成電路，文獻［2］將三段氣隙區域等效為三段電阻，通電線圈等效為電流源，構建了簡便的磁路等效電路，并給予了實驗驗證，但是實驗結果明顯高出了理論計算值7.98%，主要因為忽略了磁鐵外圍的漏磁。文獻［3］采用了神經網絡建模研究，雖然建立了懸浮系統的動力學模型，但僅限于單向電磁鐵懸浮控制，某種程度上增加了控制難度。本文采用差動勵磁式的吸力型懸浮系統［4］，以求獲得懸浮系統中電磁力-氣隙的精確數學模型。

1 磁懸浮平臺氣隙磁場

支撐電磁鐵與導軌銜鐵之間的氣隙磁場對磁懸浮平臺的性能有至關重要的影響，研究支撐電磁鐵與導軌銜鐵之間的氣隙磁場對整個磁懸浮平臺的設計和控制都很重要［5］。就U 型導軌(結構見圖1)而言，當其氣隙磁場越接近均勻分布，則其支撐磁力越平穩，平臺魯棒性越好。V 型導軌(結構見圖2)氣隙磁場存在法向和徑向分量。法向氣隙磁場成均勻分布，與支撐電流作用產生法向磁力，也就是平臺的磁吸力，與平臺自重平衡，達到懸浮目標;徑向氣隙磁場以中心線為對稱軸成對稱分布，產生徑向力，徑向力會對平臺水平驅動產生橫向擾動。

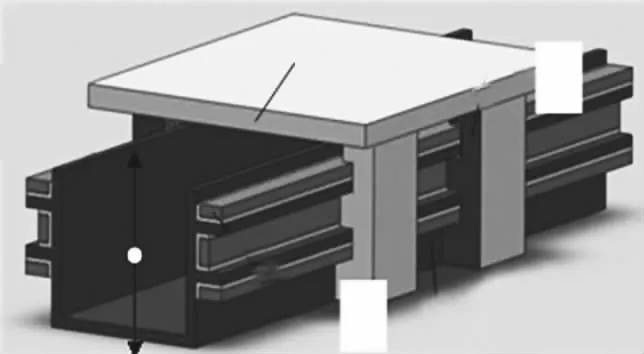
圖1 U 型導軌結構圖

圖2 V 型導軌結構圖

磁懸浮平臺磁路由支撐電磁鐵內部磁路、第一段氣隙磁場和支撐導軌內部磁路以及第二段氣隙磁場四部分組成。圖3 為差動勵磁式的吸力型懸浮系統的結構示意圖。

圖3 差動勵磁式的吸力型懸浮系統的磁路示意圖

E 型電磁鐵等同兩個U 型電磁鐵橫向疊加而成，線圈繞在E 型電磁鐵中間扼臂上，線圈通電后產生雙回路磁路，根據平臺上載荷變化的信號，實時調節控制電流值，使工作氣隙穩定在一定的允許范圍內。

2 磁力-氣隙數學模型

2.1 E 型電磁鐵選材

硅鋼散熱性能好，能滿足所設計要求，但造價較高，加工比較困難，尤其是表面粗糙度不能滿足;坡莫合金和鐵氧材料都是較好的導磁材料，但是造價昂貴;碳鋼造價不高且易于加工符合要求，剩磁較大，對磁懸浮工作臺控制有較大影響;相對而言，純鐵導磁能力較好，造價較低，易于加工，因此，純鐵是E 型鐵較理想的材料［6］。

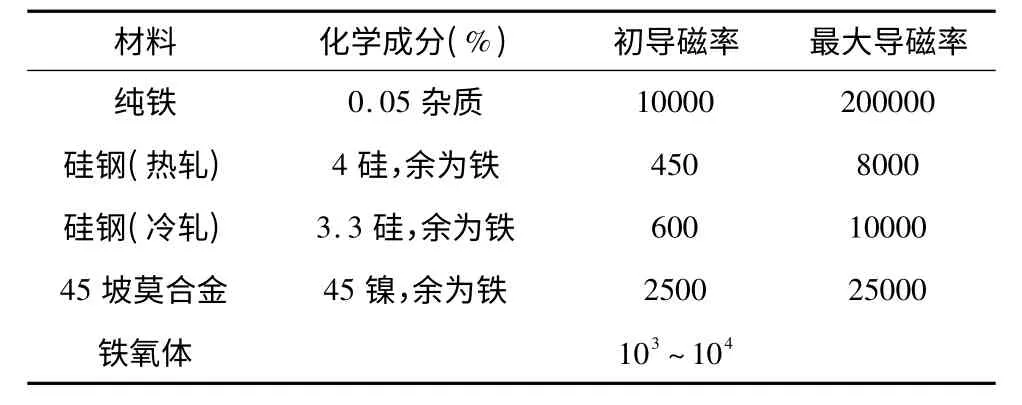
表1 幾種常見軟磁材料的性能

2.2 氣隙-漏磁通數學模型參數的確定

μE、μg——分別是E 型鐵、支撐導軌的磁導率;

μ0——空氣磁導率，通常取1.256 ×10-6H/m;

δ——氣隙值，預設的工作變化范圍0. 25 -0.30mm

磁懸浮平臺與支撐導軌采用精密的整體裝配，氣隙公差尺寸確定0.30-0.05mm。Agap1、Agap2氣隙處工作截面積，AE和Ag分別是電磁鐵扼臂截面積和支撐導軌工作段截面積。

E 型電磁鐵有三段扼臂，截面積分別記為A1，A2和A3，A2=2A1=2A3。氣隙有效工作區域與E 型電磁鐵扼臂截面積相差無幾，為簡化理論計算，預設

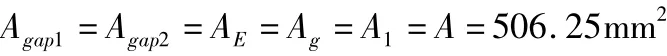
采用漆包銅質線圈，無負載時控制電流值2A，軟鐵飽和磁感應強度Bm=1.62T，線圈匝數N=192，最大偏執電流I=2A，ΦE為工作段磁通量。

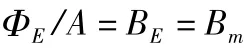
2.3 氣隙-漏磁通數值分析

依據磁路安培環路定律:Hg、HE、Hδ分別是導軌段、電磁鐵段和氣隙段磁場強度，單位A/m;lg、lE、δ 分別是導軌段、電磁鐵段和氣隙段磁路長度，單位mm;Le是總磁路長，單位mm。

懸浮平臺工作時，通入懸浮控制電流I，可認為通電線圈為磁場源。由于線圈緊密纏繞E 型電磁鐵中心扼臂，類似于通電螺線管，線圈激發產生的磁場能絕大部分傳遞至被包裹的電磁鐵，剩余磁能與發熱線圈疊加作用，經過熱交換散失在空氣中。

由于存在一定高度的氣隙，主磁通由E 型電磁鐵扼臂流向工作氣隙時，磁能損失較多，具體表現在漏磁通。設定磁通散失系數α，采用相同材質的鐵磁材料做為E 型電磁鐵和工作導軌，磁通由E 型電磁鐵流向工作氣隙的散失系數和磁通由支撐導軌流向工作氣隙的散失系數相同。表現在直流線圈激發的主磁通未全部沿著工作扼臂流向工作氣隙，稱之謂扼臂散失磁通，

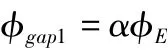
表現在主磁通未全部沿支撐導軌流向下一個工作氣隙，稱之謂導軌散失磁通，

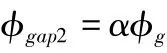
總漏磁通

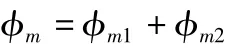
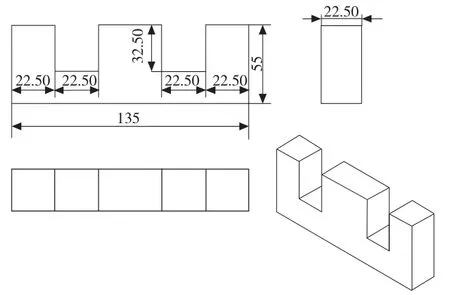
圖4 設計的E 型電磁鐵尺寸圖

第一項為氣隙工作有效磁能段，第二項為非工作散失磁能段。

比較空氣磁導率和軟鐵磁導率，兩者之間相差超過9 個數量級，即μE＜＜μ0，μg＜＜μ0，可以忽略兩項。

于是

運用Matlab 軟件對數學模型進行數值計算，對于氣隙從0.25mm 至0.30mm 之間的變化，每隔0.05mm取點。

圖5 漏磁通-氣隙關系圖體

E 型磁鐵的吸引力產生在具有不同磁導率μ 的界面［7］上，電磁吸力的計算以磁場能量為基礎，設存儲在空氣氣隙的能量為W，則

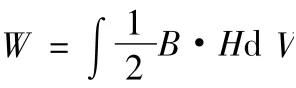
由于V=A1·δ+A2·δ+A3·δ=4A·δ，故

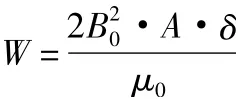
對于小位移dδ，氣隙內磁通Φ 保持不變，當氣隙δ增加dδ 時，體積V也增加dV，而磁場能W也增加dW，由虛位移原理得吸引力F:

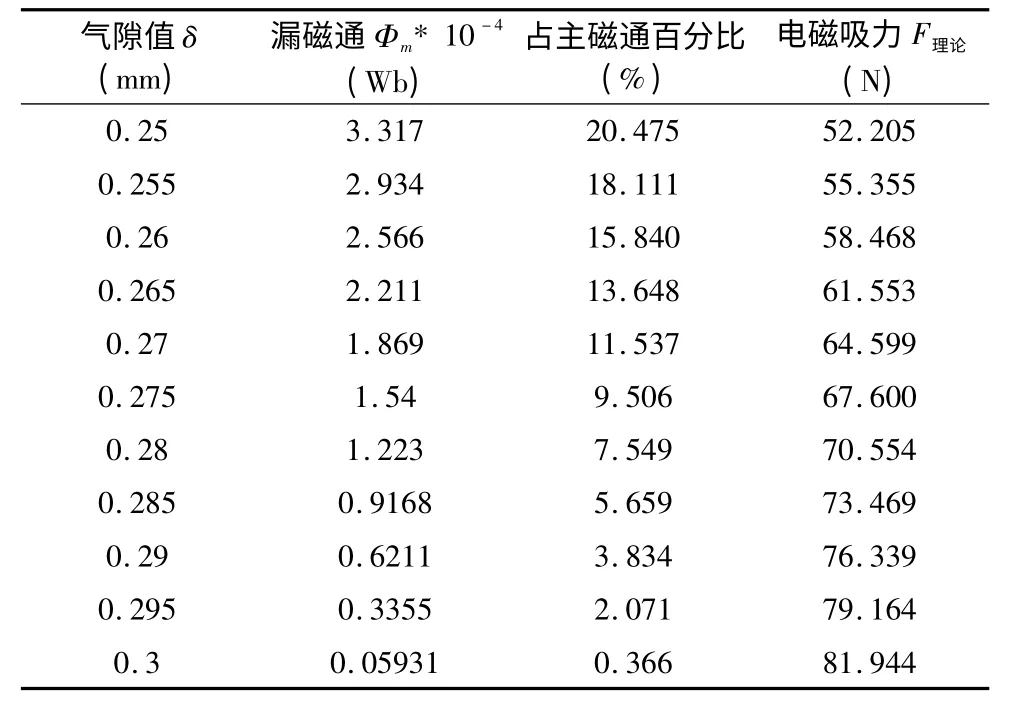
表2 氣隙、理論電磁鐵吸力關系

從表2 中可以看出，氣隙在0.275mm 到0.3mm范圍內逐次增加時，漏磁通占主磁通的百分比低于10%，氣隙處磁場吸力從67.6N 增至81.944N，上升比例超過20%。表明電磁力是由氣隙磁場和漏磁場共同產生的，漏磁場對電磁力也有貢獻［8］。為了進一步驗證建立的氣隙-漏磁通數學模型的可靠性，運用有限元分析軟件對該模型予以仿真計算。

3 漏磁通-氣隙數學模型有限元仿真

3.1 建立三維有限元模型

圖6 E 型電磁鐵三維有限元模型圖

如圖6 所示，電磁鐵選用高磁導率的純鐵材料，純鐵磁導率大，磁滯耗低，易退磁，發熱小，造價較低。其密度為7.8 ×103kg/m3，彈性模量為206Gpa，泊松比η=0.3。支撐導軌選用球墨鑄鐵。

3.2 計算結果及分析

通電線圈是系統的磁場源，在材料描述中已經對它的磁特性進行了定義，有限元法在處理通電線圈時自動將其轉化為等效電流并加載到每個單元和節點上。對剖分后的有限元模型進行加載求解，對求解結果進行分析，得如圖7 所示的三維模型的磁通密度矢量圖。

由圖8 可以看出，磁力線大部分穿過由E 型電磁鐵扼臂、氣隙和支撐導軌組成的磁回路，而在氣隙附近磁通密度明顯稠密，且存在漏磁現象，說明開環磁路系統漏磁存在的必然性。

圖7 E 形電磁鐵三維磁通密度矢量圖

圖8 E 形電磁鐵二維磁力線分布圖

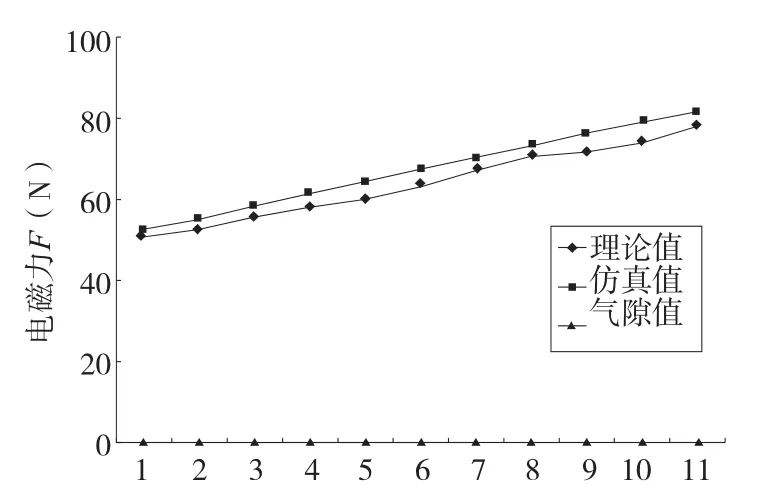
圖9 電磁力理論計算結果與仿真結果對照圖

由圖9 可知，根據建立的數學模型求出的理論電磁力略大于仿真實現的結果，在氣隙值為0. 295mm時，仿真結果低于理論值約5.23%，達到最大變化范圍。經分析認為，在整個仿真過程中，設置的電磁鐵和支撐導軌的導磁率為固定值，不符合磁懸浮平臺實際工作情況，磁懸浮平臺樣機的電磁鐵選用純鐵材料，支撐導軌選用球墨鑄鐵材料，材料本身的導磁率存在一個變化范圍，受線圈直流大小變化的影響，這種變化是非線性的。圖8 中二維漏磁場［9］仿真顯示的信息僅是整個磁路的正視剖面圖，而圖7 三維漏磁場仿真顯示了整個磁路空間的漏磁信息，改變了電磁力的仿真值。因此如何有效的增加二維磁場仿真和三維磁場仿真之間的聯系是進一步研究漏磁通影響的關鍵。

4 結論

在磁懸浮平臺的開環磁路中，建立漏磁通-氣隙數學模型并通過有限元仿真驗證，確定了漏磁通的存在，側重從氣隙角度控制漏磁通的影響，實現了對漏磁通和電磁力之間關系的研究，借鑒改進后的數學計算模型，可以為磁懸浮平臺樣機以后的調試工作提供實際參考價值。

［1］石佳. 機床進給磁懸浮系統的非線性控制方法研究［D］. 沈陽:沈陽工業大學，2008.

［2］興濤，楊建波，郭永獻. U 型磁鐵磁路分布與氣隙磁感應強度［J］. 機械設計與制造，2008(7):82 -83.

［3］Longxue Xiao，Guoqing Wu，Xudong Zhang. Modal Analysis of Maglev Linear Feed Unit. Applied Mechanics and Materials，2012，150:205 -211.

［4］黃毅. 基于dSPACE 的磁懸浮運動平臺控制方法研究［D］. 長沙:中南大學，2009.

［5］Jaewook Lee，Ercan M. Dede and Tsuyoshi Nomura. Simultaneous Design Optimization of Permanent Magnet，Coils，and Ferromagnetic Material in Actuators. IEEE TRANSACTIONS ON MAGNETICS，2011，47(12):4712 -4716.

［6］Wohlfarth. 鐵磁材料:磁有序物質特性手冊第二版［M］.北京:電子工業出版社，1993.

［7］肖龍雪. 磁懸浮直線進給單元結構設計［D］. 南通:南通大學，2011.

［8］紀鳳珠，王長龍，陳正閣，等. 基于三維有限元法的漏磁場分析［J］. 兵工學報，2007，28(7):876 -879.

［9］Lee J Y，Lee S J ，Jiles D C ，et al. Sensitivity analysis of simulations for magnetic particle inspection using the finiteelement method. IEEE Transactions on Magnetics，2003，39(6):3604 -3606.