基于光學標靶與測距儀的隱藏區域坐標測量

范宜艷，趙 斌，馬國鷺

（1.華中科技大學機械科學與工程學院，武漢430074；2.湖北工業大學機械工程學院，武漢430068）

基于光學標靶與測距儀的隱藏區域坐標測量

范宜艷1，2，趙 斌1*，馬國鷺1

（1.華中科技大學機械科學與工程學院，武漢430074；2.湖北工業大學機械工程學院，武漢430068）

為了解決大型裝備中隱藏區域的空間坐標測量問題，提出一種基于光學標靶與測距儀的激光測頭，該測頭與全站儀或激光跟蹤儀構成非接觸測量系統。測量時，激光測距儀發出的激光對準被測點測得其距離，用全站儀或激光跟蹤儀瞄準光學標靶，實時獲取激光測頭的空間坐標，同時激光測頭測得其自身的空間姿態角，然后通過坐標變換得到被測點的空間坐標；并進行了實驗驗證。結果表明，該測量系統可以使得組合測量的量程擴大并保持較高的空間坐標測量精度。

測量與計量；空間坐標測量；隱藏區間；非接觸測量；激光測距儀

引 言

空間坐標的測量在工業領域中有著廣泛的需求，如航天航空領域、船舶工業、高速列車、衛星天線等大型裝備領域［1］。目前，基于全站儀或者激光跟蹤儀的空間坐標測量系統是在大尺寸空間坐標測量領域中應用最廣的系統［2-5］。

在大型裝備的測量中［6］，常因空間阻隔、遮擋、被測點凹陷等因素導致被測件上的某些區域無法被測量。目前，針對這類問題，通常采用探針與激光跟蹤儀或全站儀器所構成的組合測量系統進行測量［7-10］，其原理是通過對探針空間位置和姿態的測量，根據坐標變換便可計算出被測點的空間坐標。然而探針測桿的長度有限，一般在1m以內，因此只適合近距離隱藏點的測量，滿足不了大型設備遠距離測量的需要，而且由于是接觸式測量，測量過程中可能會引起工件的變形或損壞。這時，需要一種非接觸式測量來彌補這些不足。

本文中將激光測距儀取代接觸式測桿，與光學標靶相結合構成激光測頭，并與全站儀或激光跟蹤儀構成非接觸測量系統。由于選用的激光測距儀測量范圍為0m～10m，因此可大大增加隱藏點空間坐標測量的距離。

1 測量系統的構成

空間坐標測量系統如圖1所示，由全站儀（或激光跟蹤儀）、激光測頭和電腦構成。其中激光測頭包含光學標靶系統和激光測距儀兩部分，并且激光測距儀的指向方向是可以調節的，光學標靶系統的結構見參考文獻［11］。

Fig.1 Structure of measuring system

測量時，將激光測距儀發出的激光對準被測點，測出激光測頭內基準點到被測點的距離，全站儀對準光學標靶系統的角錐反射鏡，實時獲取光學標靶系統在全站儀坐標系下的空間坐標，同時光學標靶測得其自身的空間姿態角，最后根據坐標轉換即可獲取被測點的空間坐標。

該測量系統通過改變激光測距儀激光的指向方向，可以適應不同方位隱藏點的空間坐標測量。

2 測量原理

2.1 測量系統的坐標系

Fig.2 Coordinate systems of measuring system

測量系統的坐標系如圖2所示，全站儀是典型的球坐標測量儀，球坐標系為O-xtytzt，轉換成笛卡爾直角坐標系O-xyz，作為測量系統的參考坐標系；激光測頭坐標系O′-xsyszs以角錐反射鏡的頂點為坐標原點，Os-zs為光軸方向，輔助參考坐標系O′-x′y′z′由參考坐標系O-xyz空間平移得到；激光測距儀坐標系Ol-xlylzl以傳感器端面出射光點為坐標原點，由O′-xsyszs平移得到。各坐標系均為右手坐標系。

2.2 測量原理

測量時，整體轉動激光測頭，使激光測距儀的激光對準被測點M，得到測距值L，全站儀瞄準光學標靶系統的角錐反射鏡，實時獲取其在全站儀坐標系下的坐標（x0，y0，z0），同時光學標靶測得其自身的空間姿態角（η，β，γ）。根據坐標變換關系，便可得M點的空間坐標（xM，yM，zM）：

式中，η，β和γ分別為光學標靶測得的滾動角、俯仰角和水平方位角，可通過光學標靶系統內各傳感器得到［11］；（xM′，yM′，zM′）為被測點M在激光測頭坐標系O′-xs-ys-zs下的空間坐標，它可根據激光測距值L計算出。

由圖2可知，激光測距儀坐標系與激光測頭坐標系的方向保持一致，所以M點在激光測頭坐標系下的坐標（xM′，yM′，zM′）與其在激光測距儀坐標系下的坐標（xl，M，yl，M，zl，M）的關系可通過平移矩陣得到：

式中，tx，ty和tz是平移參量。

被測點M在激光測距儀坐標系下的坐標（xl，M，yl，M，zl，M）為：

式中，α和φ分別為被測點在激光測距儀坐標系Olxlylzl中的水平方位角和垂直方位角。

由（2）式和（3）式可得到被測點M在激光測頭坐標系O′-xsyszs下的空間坐標：

式中，未知參量tx，ty和tz以及α，φ是無法直接得到的。若令kx＝sinαcosφ，ky＝cosα，kz＝sinαsinφ，則有：

可見是L的線性函數，其各項參量可通過標定得到。

全站儀瞄準光學標靶測量出其空間坐標，數學描述如下式所示：

式中，（xj，yj，zj）是全站儀參考坐標系O-xyz的基準點坐標，S，βt和γt分別是光學標靶在全站儀坐標系O-xtytzt中的空間斜距、俯仰角和水平方位角。

將（5）式和（6）式帶入（1）式，得到被測點M在全站儀坐標系下的空間位置坐標：

在測量過程中，全站儀以自動跟蹤模式對準光學標靶，測得其在全站儀坐標系下的斜距S、俯仰角βt和水平方位角γt。由全站儀、激光測距傳感器和光學標靶的測量數據，根據（7）式便可計算出被測點的空間坐標。

2.3 測量系統參量的標定

由上述測量系統的數學模型（7）式可知，如果已知激光測距儀坐標系與激光測頭坐標系的相對位置關系，就可通過矩陣計算得到目標點的空間坐標。測量系統的標定就是求解（5）式中的參量tx，ty和tz以及kx，ky，kz。

測量系統參量標定過程示意如圖3所示，其具體方法為：激光測頭的位姿保持不變，在激光測距儀射出的光線上的任一位置放置一球型空心角反射器（簡稱R），得到此時的測距值L1，然后用全站儀分別瞄準光學標靶和球型空心角反射器，得到光學標靶的角錐反射鏡坐標（x0，y0，z0）和R的中心點坐標（xM，1，yM，1，zM，1），以及其它姿態角參量η，β和γ，代入方程（1）式解出R在激光測頭坐標系下的坐標（xM，1′，yM，1′，zM，1′）；沿著激光線改變R的位置，重復以上測量過程兩次以上，得到L1，L2，…，Ln等，代入以下方程組：

解以上各超定方程組，可得到參量（kx，tx），（ky，ty）和（kz，tz）。

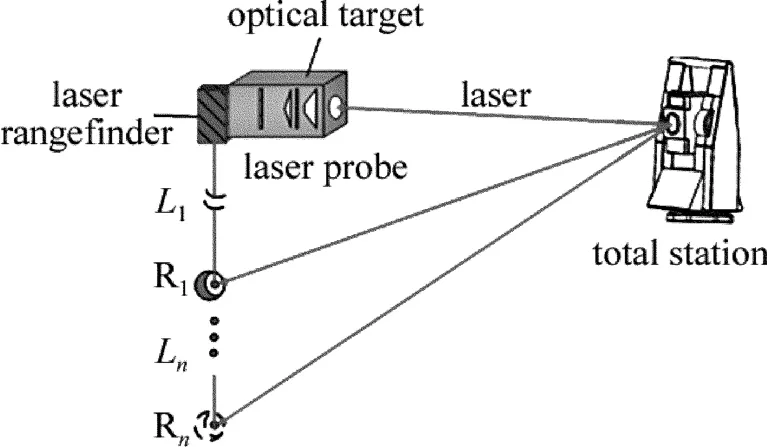
Fig.3 Calibration of the measuring system

理論上只需要測量激光線上的兩個位置點即可，實際標定中，應多測幾個點以減小誤差的影響。

實際標定中，選取5個位置點，標定得到參量值為（kx，tx），（ky，ty）和（kz，tz）分別為（－0.8213，0.2181），（－0.2765，0.2195），（0.4990，0.0283）。

在標定出測量系統各個參量后，即可計算出被測點的3維空間坐標。由于光學標靶的姿態角轉動范圍是有限的，為了對全空間范圍的坐標點進行測量，往往需要改變激光測距儀相對于標靶的安裝方位，每次重新安裝后，都應按以上步驟進行重新標定，得到新的參量。

3 測量不確定度

根據1995年出版的《測量不確定度的評定指南》，系統的合成不確定度可表示為［12］：

式中，y和xi分別表示間接測量值與直接測量值，并且y＝f（x1，x2，…，xn），uc（y）是變量xi的標準不確定度。根據測量不確定度原理（7）式和（9）式，組合測量系統的合成不確定度表示為：

式中，uc（xM），uc（yM）和uc（zM）分別是被測點的空間坐標不確定度；而uc（S），uc（βt）和uc（γt）分別對應于全站儀直接測量的光學標靶坐標系原點在全站儀坐標系中的斜距、俯仰角以及水平方位角的標準不確定度，這3個量由全站儀系統所決定；uc（η），uc（β）和uc（γ）分別是光學標靶的滾動角、俯仰角和水平方位角的標準不確定度；uc（L）是激光測傳感器的標準不確定度。

4 實驗及結果分析

針對圖1所示的全站儀與激光測頭構成的測量系統，在對系統進行了標定后，進行了空間點位測量，并與全站儀對同一空間點坐標的直接測量結果進行了比較，通過測量對比來驗證本系統的測量精度。全站儀的測角精度為2′、測距精度為2mm±1μm。采用球型空心角反射器作為被測目標進行測量實驗。

實驗步驟如下：首先用全站儀對準激光測頭的光學系統，同時激光測距儀發出的激光對準球型空心角反射器，于是根據其變換關系得到被測點在全站儀坐標系下的空間坐標；然后，保持激光測頭在空間位姿不變，轉動全站儀（此時全站儀的位置保持不變）對準球型空心角反射器，直接測量出被測點的空間坐標；接著調整激光測頭的姿態和空間位置，同時移動球形空心角反射器的到不同的位置，重復上述步驟，獲得多組測量數據，部分數據如表1所示。

Table 1 Coordinates of laser probe in different positions and measured by the combined system and by the total station instrument／m

實驗中由于全站儀測量的斜距S范圍從0m到50m，則其標準不確定度為uc（S）＝2mm，俯仰角及水平方位角的標準不確定度為uc（βt）＝uc（γt）＝0.0097mrad。而無衍射光光學標靶的姿態角的標準不確定度分別為uc（η）＝0.8341mrad，uc（β）＝0.1745mrad和uc（γ）＝0.3964mrad。激光測傳感器在10m測量范圍內的標準不確定度uc（L）＝1mm。根據（10）式，通過組合測量系統測量得到空間坐標的合成不確定度如表2所示。實驗結果表明，被測點的空間坐標不確定度（uc（xM），uc（yM），uc（zM））是（2.853，2.781，2.901）mm。

Table 2 Combined standard uncertainty of coordinates measured by the optical target in different positions and attitudes

5 結 論

本測量系統利用光學標靶的高精度角度測量，再加上激光測距儀的光學測距精度，這樣就使得測得的角度和距離精度都很高，確保了組合測量中的空間坐標的測量精度，而且由于激光測距儀的測量范圍大，大大增加了組合式空間坐標測量的距離，可廣泛應用于大型裝備的隱藏點空間坐標大量程、非接觸、動態測量。

［1］ ZHU JG，YE Sh H，YANG X Y，et al.On-line industrial 3-D measurement techniques for large volume objects［J］.Key Engineering Materials，2005，295／296（10）：423-430.

［2］ YU C L.Measurement method based on total station in 3-D measurement system［J］.Optical Instruments，2010，32（2）：1-4（in Chinese）.

［3］ CHEN H P，ZHAO B.Space coordinate measurement based on theodolites and rangefinders［J］.Laser Technology，2013，37（1）：77-81（in Chinese）.

［4］ ZHANG Ch F，ZHANG J，TANG W Y，et al.Application of laser tracker on geometric parameters measurement of large dimensional workpieces［J］.Tool Engineering，2002，36（5）：26-28（in Chinese）.

［5］ NAKAMURA O，GOTO M.Development of a coordinate measuring system with tracking laser interferometers［J］.CIRP Annals-Manufacturing Technology，1991，40（1）：523-526.

［6］ CUYPERSA W，van GESTELB N，VOETA A，et al.Optical measurement techniques for mobile and large-scale dimensional metrology［J］.Optics and Lasers in Engineering，2009，47（3／4）：292-300.

［7］ ZHAO P，NIGQ.Precise curved surface area measurement with a light-pen vision measurement system［J］.Optik，2010，121（20）：1852-1858.

［8］ XIAO Zh Zh，JIN L，YU D H，et al.A cross-target-based accurate calibration method of binocular stereo systems with large-scale field-of-view［J］.Measurement，2010，43（6）：747-754.

［9］ LAU K C.Accurate target orientation measurement system：US，007400416［P］.2008-07-15.

［10］ MA G L，ZHAO B，FAN Y Y.Non-diffracting beam based probe technology for measuring coordinates of hidden parts［J］.Optics and Lasers in Engineering，2012，51（5）：585-591.

［11］ CHEN H，ZHAO B.Electric target based on non-diffracting beam and error analysis［J］，Opto-Electronic Engineering，2011，38（2）：34-40（in Chinese）.

［12］ INTERNATIONAL ORGANIZATION FOR STANDARDIZATION.Guide to the expression of uncertainty in measurement［M］.Sevres，France：International Organization for Standardisation Geneva ISO，1995：1-120.

Coordinate measurement system of hidden parts based on optical target and rangefinder

FANYiyan1，2，ZHAOBin1，MA Guolu1
（1.School of Mechanical Science Engineering，Huazhong University of Science and Technology，Wuhan 430074，China；2.School of Mechanical Engineering，Hubei University of Technology，Wuhan 430068，China）

In order to solve the coordinate measurement of hidden parts in large equipment，a laser probe based on optical target and rangefinder was proposed，which was combined with a total station instrument or a laser tracker to form a non-contact measurement system.During the measurement，the laser beam from the rangefinder was set to touch the measurement point and the distance between the rangefinder and the point was measured.And then，the optical target was aimed at by the total station instrument or the laser tracker.The spatial coordinates and the attitude angles of the laser probe were gotten.Finally，the spatial coordinates of the measured point was calculated by coordinate transformation.After theoretical analysis and experimental verification，the results show that the measurement system could expand the measurement range and achieve reliable and higher measurement precision.

measurement and metrology；space coordinate measurement；hidden parts；non-contact measurement； laser rangefinder

TH761

A

10.7510／jgjs.issn.1001-3806.2014.06.001

1001-3806（2014）06-0723-06

國家九七三重點基礎研究發展計劃資助項目（2013CB035405）

范宜艷（1975-），女，博士研究生，講師，主要從事精密測量方面的研究。

*通訊聯系人。E-mail：zhaobin63＠sohu.com

2013-12-17；

2014-02-25