多次隨機載荷下結構動態可靠性預測的概率密度演化方法

方永鋒，陳建軍，閻 彬，曹鴻鈞

（1畢節學院 機械工程學院，貴州 畢節 551700；2西安電子科技大學電子裝備結構設計教育部重點實驗室，西安710071）

多次隨機載荷下結構動態可靠性預測的概率密度演化方法

方永鋒1，陳建軍2，閻 彬2，曹鴻鈞2

（1畢節學院 機械工程學院，貴州 畢節 551700；2西安電子科技大學電子裝備結構設計教育部重點實驗室，西安710071）

文中給出了多次隨機載荷下結構動態可靠性預測的概率密度演化方法。首先利用一次作用載荷的概率分布函數，求得多次作用載荷的概率密度函數。在考慮結構承受多次隨機載荷作用下結構強度退化和不退化的情況下，根據應力-強度干涉理論和概率密度演化方法，建立了結構的動態可靠度預測模型。應用向前差分方法求解該模型中的概率密度演化微分方程，獲得任意時刻結構強度裕度的概率密度函數，進而再利用積分方法獲得結構動態可靠度的預測結果。最后通過兩個算例表明，該方法實用易行，且具有較高的計算精度。

概率密度演化；隨機載荷；結構；動態可靠性；模型

1 引 言

結構的可靠性是評價結構性能的重要指標之一。關于結構的經典可靠性研究已有很多文獻進行了描述[1-3]，主要的方法有一次二階矩方法（First Order Second Moment Method，FOSMM）、蒙特卡洛方法（Monte Carlo Method，MCM）等。文獻[4-7]研究了結構的動力可靠性問題，主要是針對結構承受一次動載荷進行可靠性分析，但整個分析過程未考慮結構的強度與時間的關系。在某些實際問題中，結構在其服役期內不但承受的隨機載荷是時變的，且結構本身因老化、腐蝕、磨損、振動松弛等多種原因，使其強度值也隨時間退化。文獻[8-9]研究了機械零部件與系統的動態可靠性問題，表明零件與系統的失效率也是滿足浴盆曲線的。文獻[10]給出了一種考慮共同載荷下結構的動態可靠性預測模型，該模型比較實用可行，但利用一次二階矩方法來計算結構的可靠度，當結構的應力和強度兩隨機變量之一不服從正態分布時，所得的結構可靠度為近似值。多年來，人們一直在探索對結構可靠性精確計算的方法，而完全概率分析方法則提供了一種新的思路。該方法的基本作法是根據激勵隨機變量的分布概型和系統激勵與響應之間的傳遞函數關系，利用隨機數學中的相關方法，設法獲得結構隨機響應量完整的概率信息，包括響應量的概率分布函數和數字特征，再利用可靠性分析中的積分方法，獲得結構可靠度的準確計算結果。近年來出現了利用概率密度演化方法（Probability Density Evolution Method，PDEM）研究結構的靜力和動力可靠性問題[11-13]，該方法能夠全面地反映隨機模型的概率信息，可得到隨機結構的靜、動力響應量的概率密度函數。

本文在以上文獻的基礎上，在已知載荷應力與結構強度的概率分布函數的前提下，根據應力-強度干涉理論，利用概率密度演化方法，建立了結構承受多次隨機載荷且結構強度隨時間不退化和退化的結構動態完全概率的可靠性預測模型，對該模型中的概率守恒微分方程利用向前差分方法求解。最后通過算例說明文中模型的合理性和方法的可行性與精確性。

2 結構動態可靠性的概率密度演化方程

2.1 強度不退化時的結構動態可靠性的概率密度演化方程

考慮結構在其服役期內，承受多次隨機載荷的作用，但結構的強度不退化。記一次載荷為S，與它對應的應力隨機變量為s，s的概率分布函數和概率密度函數分別為G（s）和g（s）。當隨機載荷S對結構作用n次時，相當于從載荷母體中抽取了n個載荷樣本，若結構在這n次隨機載荷中的最大載荷Smax作用下不失效，顯然結構在這n次載荷作用下也不會失效。為此，從偏于安全的觀點，可用載荷樣本中最大載荷作用n次下結構的可靠度作為n次隨機載荷作用下結構的可靠度，即將n次最大載荷作為結構可靠性預測的等效載荷。

隨機載荷作用n次時的等效載荷Smax的對應的應力隨機變量smax的概率分布函數為：

通常載荷的發生是服從參數為λ的Possion分布的[9]，由此則可得在t時刻應力的概率分布函數為：

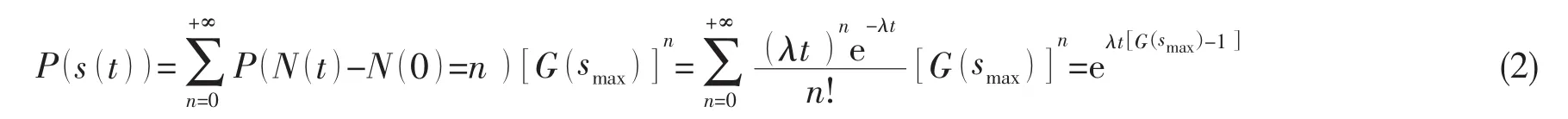
式中：N（t）為時段 [0,t]內載荷出現的總次數，N（0）為在0初始時刻載荷出現的次數，n為從0到t時刻載荷發生的次數。

由（2）式可得在t時刻應力對應的概率密度函數為：

由于結構的強度隨機變量δ不隨時間退化，可設δ的概率密度函數為f（δ）且已知，則根據應力—強度干涉理論，可得結構在多次隨機載荷作用下其強度裕度隨機變量r（t）=δ-smax（t）的概率密度函數為：

將（4）中的變量 smax換為 s（）t，則該式可表為：

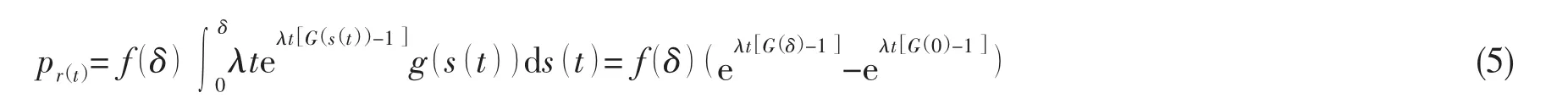
記結構在多次隨機載荷作用下強度裕度的概率密度函數為：

由于在結構服役過程中，無新的隨機因素加入，即沒有新的概率源產生，故p δ,t0（）滿足概率守恒原理，即滿足如下微分方程：

該方程為一維經典的Liouville方程，其中a（）τ為Dirac函數，方程的初始條件為：

求解由（7）式和（8）式給出的偏微分方程初值問題，即可獲得結構強度裕度r（t）的概率密度函數p（δ,t），進而再利用積分方法可得結構動態可靠度R（t）的精確計算表達式為：

上式即為結構在多次隨機載荷作用且強度不退化情況下、在任意t時刻的動態可靠度預測模型。

2.2 強度退化時結構動態可靠性的概率密度演化方程

考慮結構在其服役期內承受多次隨機載荷的作用，且結構的強度隨機變量將隨時間而退化，對于結構在 τ時刻其剩余強度 δ（τ）的概率分布函數H[ δ（ τ ）]可以 Weibull分布來描述[15]，即：

式中：β（τ）、η（τ）和 γ（τ）為實時的Weibull分布參數，τ為結構在服役期T內的工作時間。

由上式，可得 δ（τ ）的概率密度函數h[ δ（ τ ）]為：

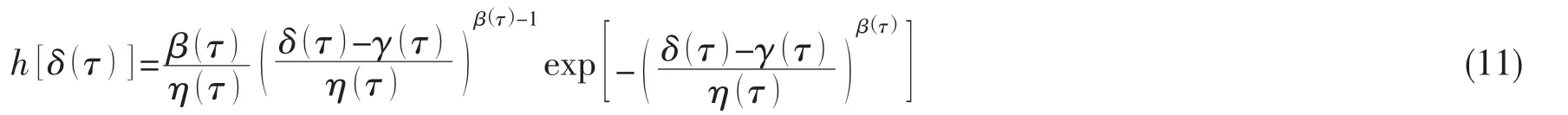
同前處理，由（5）式和（11）式可導得在多次隨機載荷作用下且結構強度隨時間退化時，強度裕度隨機變量r（t）=δ（t）-smax（t）的概率密度函數為：

記在多次隨機載荷作用下且結構強度退化時強度裕度的概率密度函數為：

由于在結構服役過程中，無新的概率源產生，故q（ δ（ 0 ）,t0）滿足概率守恒原理，即滿足如下Liouville微分方程：

該方程對應的初始條件為：

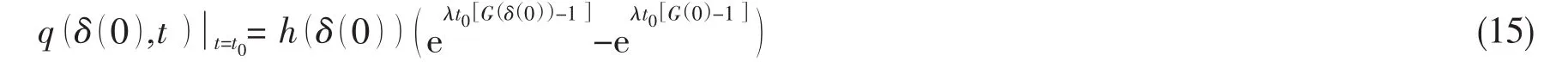
求解由（14）式和（15）式給出的偏微分方程初值問題，即可獲得結構強度裕度r（）t的概率密度函數 q（ δ（ τ ）,t），進而利用積分方法可得結構動態可靠度R（t）的精確計算表達式為：

上式即為結構在多次隨機載荷作用下且強度退化、在任意t時刻的動態可靠度預測模型。

3 概率密度演化方程的求解

由前建立的結構動態可靠度預測模型即（9）式和（16）式顯見，問題求解的關鍵須首先求解由概率密度演化微分方程（7）和（14）給出的偏微分方程初值問題。此類方程的初值問題在理論上存在著形式上的解析解[8]，但在實際計算中，該形式上的解析解通常是無法獲得的，需利用各種數值方法求解。本文則應用了向前差分格式的數值算法，其算法的主要步驟如下：

Step1.對變量和初始條件進行離散，初始條件（8）和（15）被分別離散化為：

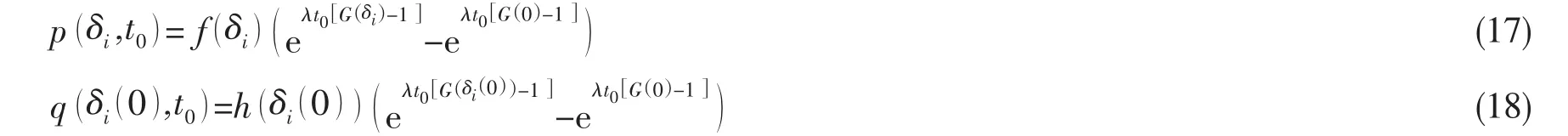
其中：δi=i·Δδ，Δδ為 δ方向的劃分；δi（t）=i·Δδ（t），Δδ（t）為 δ（t ）方向上的劃分，i＝0，1，2，…。

對時間 t進行離散，tj=j·Δt，Δt為 t方向的劃分， j＝0，1，2，…。

令網格比 λ1=Δt/Δδ，λ2=Δt/Δδ（τ），為了保證計算的收斂和穩定，要求：0＜λ1a（t ），λ2a（t）≤1。

Step2.對方程（7）和（14），分別利用如下的向前差分遞推公式進行計算：

通過上述過程的求解，即可獲得滿足方程（7）和（14）的解，即結構強度裕度隨機變量r（t）隨時間演化的概率密度函數。

4 算 例

例1.某減速箱中的一軸，考慮其強度δ不退化的情況。設：δ服從均值為110 MPa，標準差為15 MPa的正態分布。取λ=1，工作應力s服從均值為50 MPa、標準差為15 MPa的正態分布。在載荷作用多次時，取 λ1a（t）=0.5。

求解本文導出的結構強度不退化情況下的強度裕度r（t）的概率密度演化方程（7），分別獲得了在t=0，25，100 單位時間時 r（t）的概率密度函數曲線見圖1。從圖中可見，文中方法可以獲得在多次隨機載荷下結構強度不退化、在任意時刻的結構強度裕度r（t）的概率密度函數；在t=0時，r（t）的概率密度函數為正態分布，而在演化的過程中，如在t=25，t=100單位時間時，r（t）概率密度將不再為正態分布。這說明概率密度演化方法能準確刻畫結構在多次載荷作用下的結構強度不退化時的可靠度實時變化情況。由于能夠得到任意時刻r（t）的概率密度曲線，從而可得到r（t）在時域上的全部概率信息。

為進行對比，表1中同時給出了利用本文方法PDEM以及FOSMM和MCM方法（模擬n=106次）求得的該軸在t=0，25，100單位時間對應的可靠度預測結果。從計算結果看，結構的動態可靠度隨時間逐漸降低，這是因為考慮到載荷多次作用的緣故。

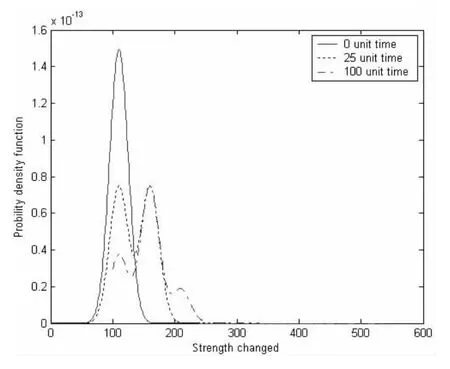
圖1 例1在t=0，25，100單位時間的概率密度Fig.1 The curves of the probability density under t=0，25，100 unit time in the example1

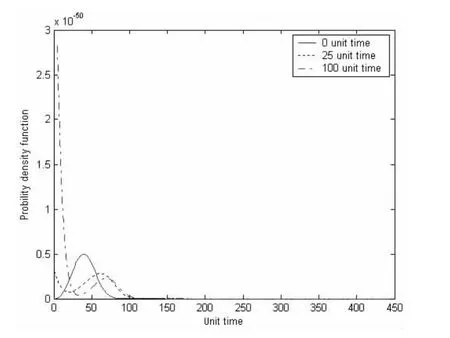
圖2 例2在t=0，25，100單位時間的概率密度Fig.2 The curves of the probability density under t=0，25，100 unit time in the example2

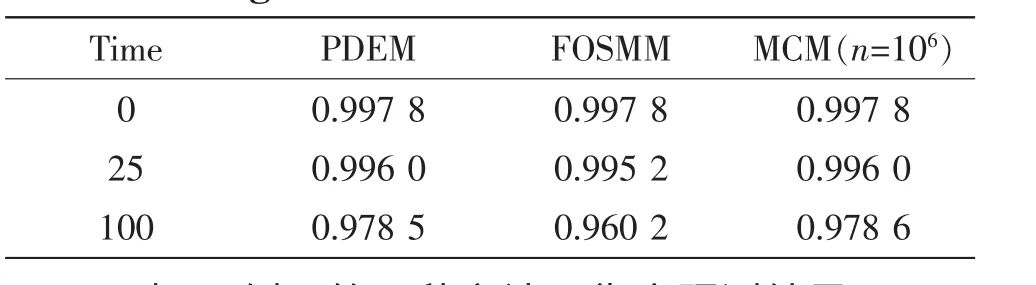
表1 例1的三種方法可靠度預測結果Tab.1 The prediction results of the example1 by using three methods

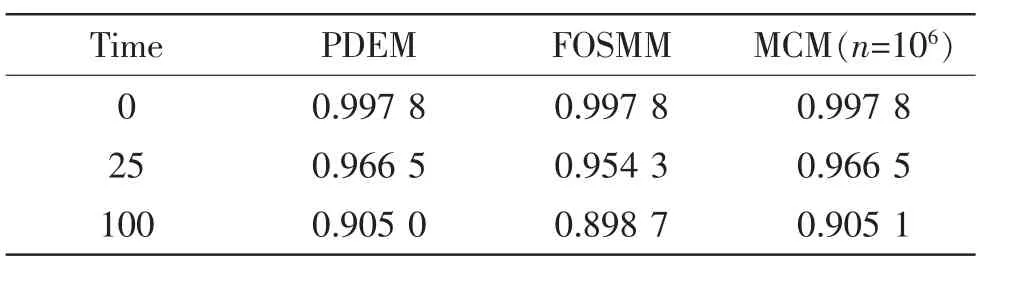
表2 例2的三種方法可靠度預測結果Tab.2 The prediction results of the example2 by using three methods

例2.結構及結構參數均同例1，但考慮結構的強度δ（t）隨時間退化的情況。

求解本文導出的結構強度退化情況下的強度裕度r（t）的概率密度演化方程（14），獲得在t=0，25，100 單位時間 r（t）的概率密度函數曲線見圖2。從圖中可見：隨著時間的增長，r（t）的概率密度曲線趨于復雜，與最初的正態分布相去甚遠，故而此時利用一次二階矩方法給出的可靠度預測結果將產生顯著的偏差；另外，隨著時間的增長，r（t）的概率密度函數曲線峰值降低，寬度增大，并且其漲落比隨機源的漲落顯著增強。這些表明：文中的方法可以給出多次隨機載荷下的結構強度退化、任意時刻的結構強度裕度的概率密度函數，能夠準確地刻畫結構動態可靠度的實時變化情況。

為進行對比，表2中同時給出了利用本文方法PDEM以及FOSMM和MCM方法（模擬n=106次）求得的該軸在t=0，25，100單位時間對應的可靠度預測結果。該結果表明，結構的動態可靠度比例1中隨時間下降的幅度更大，即在同一時刻，考慮強度退化的結構可靠度要低于強度不退化的結構可靠度。

從圖1-2可見，利用向前差分方法求解微分方程（7）和（14），其解滿足概率密度函數的非負性、完備性（密度函數曲線在橫坐標上所圍面積之和恒為1），表明本文方法關于結構強度裕度隨機變量的概率密度函數演化計算方法的正確性。

從表1-2可見，由于強度裕度隨機變量r（）t在0時刻均服從正態分布，故三種方法在0時刻的可靠度預測結果均完全相同。但隨時間演化，r（）t將不再服從正態分布，但此時本文方法與MCM對于結構動態可靠度的預測結果基本是一致，而FOSMM的預測結果誤差較大，這充分彰顯了本文方法計算結果的精確性。

5 結 論

（1）文中基于概率密度演化方法，建立了多次隨機載荷作用下結構強度退化和不退化的動態可靠性預測模型，能夠獲得任意時刻的應力-強度兩干涉量的概率密度函數，從而可得到結構動態可靠性的全部的概率信息，為準確地預測結構全生命周期的可靠性提出了一種方法。

（2）利用向前差分方法求解概率密度演化微分方程，可以保證所求概率密度函數的非負性和完備性，且算法簡單高效，易于編程實現。

（3）算例的結果表明，本文方法預測結構的動態可靠度，實用易行且具有較高的精度。

[1]Dilip R,Tanmoy D.A discretizing approach for evaluating reliability of complex systems under stress-strength model[J].IEEE Transaction on Reliability,2001,50(2):145-150.

[2]Knut O R,Gunner C L.Reliability-based design of wind-turbine rotor blades against failure in ultimate loading[J].Engineering Structures,2000,22(1):565-574.

[3]Chen Jianjun.Analysis of engineering structures response to random wind excitation[J].Computers&Structures,1994,51(6):687-693.

[4]陳建軍,車建文,馬洪波,戴 君.桁架結構動力特性可靠性優化設計[J].固體力學學報,2001,22(1):54-62.

Chen Jianjun,Che Jianwen,Ma Hongbo,Dai Jun.Dynamic optimum design on reliability for truss structures[J].Acta Mechnica Solida Sinica,2001,22(1):54-62.

[5]Gao W,Chen J J,Ma H B.Dynamic response analysis of closed loop control system for intelligent truss structures based on probability[J].Mechanical Systems and Signal Processing,2003,15(2):239-248.

[6]Salvatore Benfratello,Livia Cirone,Francesco Giambance.A multi-criterion design of steel frames with shakedown constrains[J].Computers and Structures,2006,84(5-6):269-282.

[7]宋述芳,呂震宙.基于馬爾科夫蒙塔卡羅子集模擬的可靠性靈敏度分析方法[J].機械工程學報,2009,45(4):33-38.

Song Shufang,Lv Zhenzhou.Structural reliability sensitivity analysis method based markov chain Monte Carlo subset simulation[J].Journal of Mechanical Engineering,2009,45(4):33-38.

[8]王新剛,張義民,王寶艷.機械零部件的動態可靠性靈敏度分析[J].機械工程學報,2010,46(10):188-193.Wang Xingang,Zhang Yimin,Wang Banyan.Dynamic reliability analysis of mechanical components[J].Journal of Mechanical Engineering,2010,46(10):188-193.

[9]王 正,康 銳,謝里陽.以載荷作用次數為壽命指標的失效相關系統可靠性建模[J].機械工程學報,2010,46(6):188-197.

Wang Zheng,Kang Rui,Xie Liyang.Reliability modeling of systems with dependent failure when the life measured by the number of loadings[J].Journal of Mechanical Engineering,2010,46(6):188-197.

[10]Fang Yongfeng,Chen Jianjun.Analysis of structure dynamic reliability under the together stochastic loads[J].Advances in Information and Science Technology,2012,4(8):178-186.

[11]陳建兵,李 杰.隨機載荷作用下隨機結構線性反應的概率密度演化分析[J].固體力學學報,2004,25(1):119-124.

Chen Jianbing,Li Jie.Probability density evolution of linear stochastic structural response[J].ACTA Mechanica Solid Sinica,2004,25(1):119-124.

[12]李 杰,陳建兵.隨機結構動力可靠度分析的概率密度演化方法[J].振動工程學報,2004,17(2):121-128.

Li Jie,Cheng Jianbing.Probability density evolution method for dynamic reliability analysis of stochastic structures[J].Journal of Vibration Engineering.2004,17(2):121-128.

[13]Jie Li,Jianbing Chen.The principle of preservation of probability and the generalized density evolution equation[J].Structural Safty,2008,30(9):65-77.

[14]Schaff J R,Davidson S D.Life prediction methodology for composite structures.Part I Constant amplitude and two-stress level fatigue[J].Journal of Composite Materials,1997,31(2):128-157.

Probability density evolution method of the prediction model of structural reliability from the time response under several times stochastic loads

FANG Yong-feng1,CHEN Jian-jun2,YAN Bin2,CAO Hong-jun2

(1 School of Mechanical Engineering,Bijie University,Bijie 551700,China;2 Key Laboratory of Electronic Equipment Structure Design,Ministry of Education,Xidian University,Xi’an 710071,China)

The probability density evolution of the structural dynamic prediction models under several times random loads are presented.The probability density of several times stochastic loads can be obtained by the probability density of a time stochastic load.The prediction models of the structural reliability from the time response under several times stochastic loads with the strength degeneration and without degeneration over time are constructed by using the stress-strength interference theory and probability density evolution method.The differential equation in the models can be solved by using the forward differential method.The probability density functions of the structural strength redundancy in any time can be obtained.The structural dynamic prediction reliability can be obtained by using integral method.Finally,the two given examples show that this method is practicable,feasible and more accurately.

probability density evolution;stochastic load;structure,dynamic reliability;model

TB114.3

A

10.3969/j.issn.1007-7294.2014.04.008

1007-7294（2014）04-0413-06

2013-07-12

國家自然科學基金項目資助（51175398）；畢節學院高層次人才科學研究項目（院科合字G2013007號）資助

方永鋒（1975-），男，博士，畢節學院機械工程學院副教授，E-mail:lijiemech@126.com；

陳建軍（1951-），男，西安電子科技大學機電工程學院教授，博士生導師。