柱支承無粘結預應力混凝土雙向板內力重分布

王曉東，鄭文忠，王 英（1.結構工程災變與控制教育部重點實驗室（哈爾濱工業大學），150090哈爾濱；2.哈爾濱工業大學土木工程學院，150090哈爾濱；3.哈爾濱理工大學建筑工程學院，150001哈爾濱）

柱支承無粘結預應力混凝土雙向板內力重分布

王曉東1，2，3，鄭文忠1，2，王 英1，2
（1.結構工程災變與控制教育部重點實驗室（哈爾濱工業大學），150090哈爾濱；
2.哈爾濱工業大學土木工程學院，150090哈爾濱；3.哈爾濱理工大學建筑工程學院，150001哈爾濱）

為了研究柱支承預應力混凝土雙向板中無粘結筋應力增長規律及彎矩調幅設計方法，采用ABAQUS大型有限元軟件建立了柱支承無粘結預應力混凝土雙向板的有限元分析模型.通過將雙向板劃分為柱上板帶和跨中板帶，分別考察了綜合配筋指標和非預應力筋屈服強度對無粘結筋應力增量及支座控制截面彎矩調幅系數的影響規律.分析結果表明:在綜合配筋指標和預應力度一定的條件下，正常使用階段和承載能力極限狀態無粘結筋應力增量隨非預應力筋屈服強度的提高而增大，而支座控制截面的彎矩調幅系數隨非預應力筋屈服強度的提高而減小.建立了以綜合配筋指標和非預應力筋屈服強度為自變量的柱支承預應力混凝土雙向板中無粘結筋應力增量和彎矩調幅系數計算公式.

預應力混凝土；柱支承板；有限元；無粘結筋應力增量；彎矩調幅系數

混凝土板-柱結構是房屋建筑常用的結構形式之一，而無粘結預應力的應用大大改善了結構的使用性能，使無粘結預應力混凝土板-柱結構得到了廣泛應用.但由于復雜的受力機理使得該結構的精確分析變得極為困難，而ANSYS、ABAQUS等大型有限元軟件以其較高的計算精度及龐大的數據處理能力使得這些問題有望得以解決.但由于這些有限元軟件進入土木工程領域相對較晚，以及無粘結預應力混凝土柱支承雙向板的自身特點使之在有限元分析過程中收斂性難以保證等原因，國內外此方面的研究成果還極為有限［1-4］.本文通過對無粘結筋與其周圍混凝土相互作用的等效處理，建立了無粘結預應力混凝土柱支承雙向板的有限元模型.通過模型分析結果，建立了正常使用極限狀態及承載能力極限狀態下柱支承預應力混凝土雙向板柱上板帶和跨中板帶中無粘結筋應力增量計算公式，建立了承載能力極限狀態下柱支承無粘結預應力混凝土雙向板支座控制截面彎矩調幅系數的計算公式，并提出了彎矩調幅設計方法.

1 有限元模型的建立

ABAQUS有限元軟件是一種先進的通用有限元程序系統，可解決從簡單的線性分析到較為復雜的非線性問題，具有Standard和Explicit兩個分析模塊［5-7］.本文利用Standard分析模塊對預應力混凝土結構的塑性性能進行有限元分析.

1.1 單元選擇

采用8節點六面體線性減縮積分單元“C3D8R”來模擬混凝土板，該單元具有位移結果精確的優點.為防止產生沙漏，沿板厚方向劃分4個單元.非預應力筋和無粘結筋采用桁架單元“T3D2”模擬，該單元為在空間中只能承受拉伸和壓縮荷載作用的線狀構件.

1.2 材料本構關系

1.2.1 混凝土本構模型

國內外學者提出了多種考慮混凝土塑性性能的本構模型，本文在ABAQUS分析中對混凝土采用可考慮材料拉壓性能的損傷塑性模型.該模型可模擬損傷引起的不可恢復的材料退化［8］.

對于單軸向混凝土本構模型，本文采用文獻［9］提出的混凝土單軸受拉和受壓應力-應變曲線.

混凝土單軸受壓應力-應變關系表達式為

式中：fc為混凝土的單軸抗壓強度；εc為與fc相應的混凝土峰值壓應變；αa、αd分別為單軸受壓應力-應變曲線上升段、下降段的參數值［9］．

混凝土單軸受拉時應力-應變關系表達式為

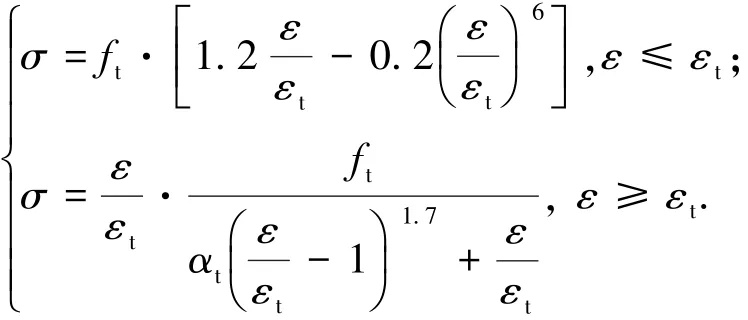
式中：ft為混凝土單軸抗拉強度；εt為與ft相應的混凝土峰值拉應變；αt為單軸受拉下降段參數值［10-11］．

在混凝土損傷塑性模型中，采用了塑性勢面與屈服面不同的不相關聯的流動法則，塑性勢面采用文獻［12］提出的靜水壓力面G為

式中：ζ為偏心率，表示塑性勢面與其漸近線接近程度的參數；σt0為混凝土的單軸抗拉強度；ψ為ˉp-ˉq應力平面中的膨脹角；ˉq、ˉp分別為等效米澤斯應力和靜水壓力．

1.2.2 預應力筋與非預應力筋本構模型

非預應力筋采用圖1所示的理想彈塑性本構模型，預應力筋本構關系采用三折線模型.

圖1 鋼材的本構關系

1.3 有限元模型的建立過程

有限元模型采用九柱四區格柱支承無粘結預應力混凝土雙向板，其中混凝土雙向板及混凝土柱均采用8節點六面體線性減縮積分單元模擬，預應力筋及非預應力筋采用桁架單元“T3D2”模擬.無粘結筋與其周圍混凝土的可相對滑動特點通過沿預應力筋全長在無粘結筋和混凝土節點間設置多個剛性Springa彈簧來模擬，.而非預應力筋與混凝土的粘結作用通過Embed命令將兩者的節點進行耦合［13］.

2 模型驗證

2.1 無粘結預應力混凝土平板-柱試驗

陶學康等［14］進行了無粘結預應力混凝土九柱四板的試驗研究.該無粘結預應力混凝土九柱四板試驗模型單跨跨度為3 m，板厚80 mm.混凝土板中采用φ6.5的非預應力筋，抗拉強度標準值fyk= 265 N／mm2；預應力筋采用fptk=1 575 N／mm2的鋼絞線.混凝土立方體抗壓強度實測平均值為28 N／mm2，板的平均預壓應力約18 N／mm2.

2.2 試驗結果分析

本文方法所計算的九柱板格板跨中的荷載-變形曲線的仿真分析與模型試驗結果對比見圖2.由圖2可知，板中心變形計算值與試驗值吻合較好，說明本文建立的有限元模型具有一定的計算精度.

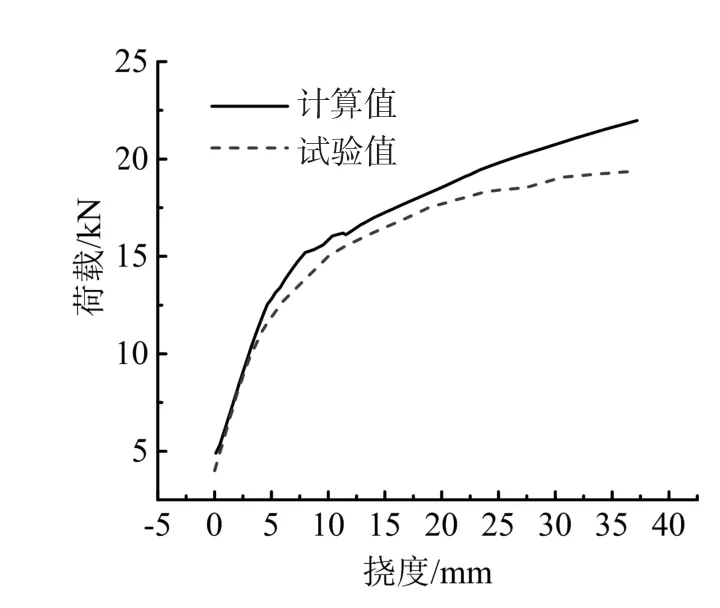
圖2 板中心變形的試驗值與計算值對比

3 雙向板參數設計

3.1 荷載確定

3.1.1 恒載

本文無粘結預應力混凝土雙向板設計中所考慮的恒荷載見表1.3.1.2 活載

表1 恒載統計

參見GB5009—2012《建筑結構荷載規范》中表4.1.1，可以發現活荷載標準值在2～5 kN／m2范圍分布最多.因此從適應實際工程應用考慮出發，四邊支承無粘結預應力混凝土雙向板的模型設計均考慮了活荷載分別為2、3、4、5 kN／m2時的情況.

3.2 板厚確定

根據實際工程經驗，無粘結預應力混凝土雙向板的跨度一般在7～10 m范圍內，故本文設計的雙向板模型中，板的跨度有7、8、9、10 m共4種類型.每種跨度下的板厚可由最小高跨比確定，應滿足：

式中l1為板的短邊跨長．

3.3 混凝土及鋼筋材料的確定

各雙向板模型中預應力筋采用抗拉強度標準值fptk=1 860 N／mm2的φs15無粘結預應力鋼絲，混凝土強度等級為C40（μfcu=49.8 N／mm2），彈性模量Ec=3.25×104N／mm2.

對于非預應力筋，根據中國近年頒布的GB 50010—2010《混凝土結構設計規范》及GB1499.2—2007《鋼筋混凝土用熱軋帶肋鋼筋》國家標準，將雙向板的模型設計考慮了非預應力筋鋼種分別為HPB300、HRB335、HRB400、HRB500、HRB600時的情況.

3.4 雙向板模型設計

本文建立的柱支承無粘結預應力混凝土雙向板中無粘結筋采用中國常用的布筋形式，在柱上板帶配置65%的無粘結預應力筋，其余預應力筋分布在跨中板帶內.

4 無粘結筋應力增量計算

4.1 無粘結筋應力增量計算方法

預應力混凝土雙向板內力的復雜性與多樣性將對無粘結筋應力增量的分析結果產生一定的誤差［15-17］.本文將通過無粘結筋在雙向板受荷后的整體變形求得其應力增量值.

4.2 正常使用階段無粘結筋應力計算

在查閱相關資料的基礎上并考慮到與預應力混凝土梁中無粘結筋應力增量計算公式相協調，在這里以單位板帶綜合配筋指標β0做為影響無粘結筋應力增量的主要參數進行分析［18］.

4.2.1 柱上板帶無粘結筋應力增量計算

以雙向板控制截面非預應力筋受拉屈服做為正常使用極限狀態的標志，基于有限元模型分析結果，可得到柱上板帶中無粘結筋在正常使用極限狀態下的應力增量Δσpyz隨綜合配筋指標β0變化關系．以配有HRB400級非預應力筋的柱支承雙向板為基礎，β0-Δσpyz計算結果見圖3．

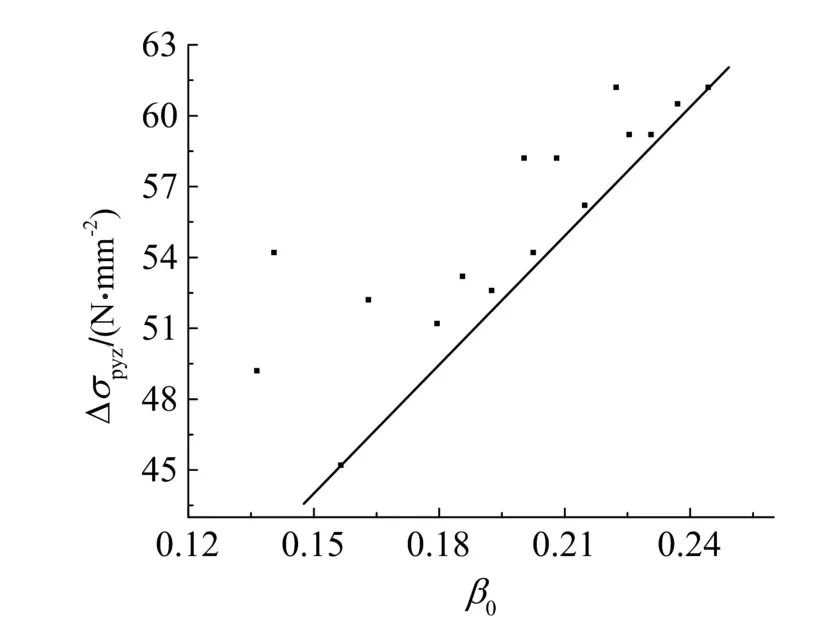
圖3 Δσpyz與β0的擬合曲線

由圖3可知，隨著β0的增大，無粘結筋應力增量呈上升趨勢．取圖3中數據點的下包線作為非預應力筋為HRB400的柱支承雙向板在正常使用極限狀態下無粘結筋應力增量ΔσpyzHRB400的公式擬合曲線，則

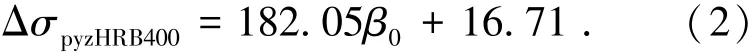
令μpyz為在柱上板帶單位板寬的綜合配筋指標β0等基本參數相同的情況下分別配有HPB300、HRB335、HRB500和HRB600非預應力筋的柱上板帶與配有HRB400非預應力筋的柱上板帶在正常使用極限狀態下無粘結筋應力增量的比值.則根據有限元模擬計算結果，可得到與非預應力筋抗拉屈服強度fy對應的μpyz關系圖，見圖4.

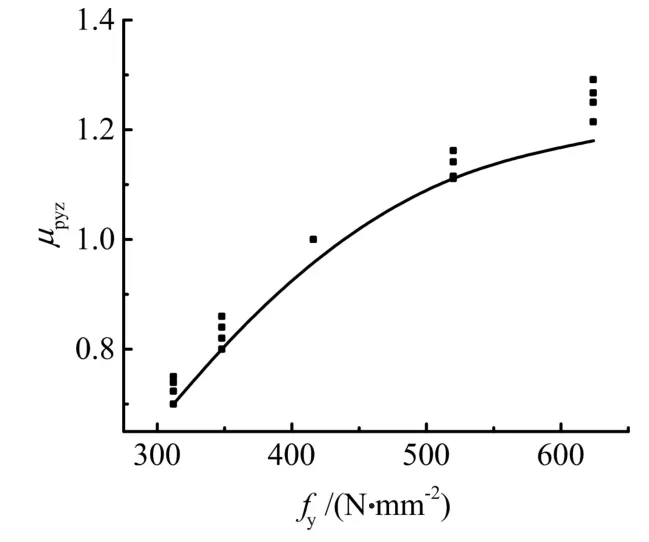
圖4 μpyz與fy關系

由圖4可知，不同非預應力筋鋼種對柱支承雙向板正常使用極限狀態無粘結筋應力增量的影響較為明顯，且隨著非預應力筋強度等級的提高無粘結筋應力增量有所提高.取圖4中數據點的下包線作為非預應力筋鋼種影響系數μpyz的方程曲線，則

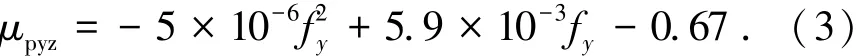
則配置任一非預應力筋鋼種的柱支承雙向板柱上板帶無粘結筋在正常使用極限狀態下的應力增量Δσpyz為

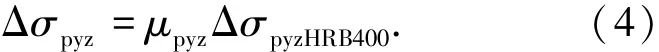
4.2.2 跨中板帶無粘結筋應力增量計算

以配有HRB400級非預應力筋的柱支承雙向板為基礎，其跨中板帶中無粘結筋在正常使用極限狀態下的應力增量Δσpym隨綜合配筋指標β0的變化關系見圖5．

圖5 Δσpym與β0的擬合曲線

由圖5可知，隨著β0的增大，無粘結筋應力增量呈上升趨勢．取圖5中數據點的下包線作為非預應力筋為HRB400的柱支承雙向板在正常使用極限狀態下無粘結筋應力增量ΔσpymHRB400的公式擬合曲線，則

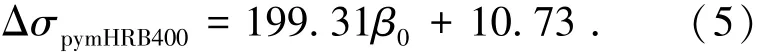
為考慮非預應力筋鋼種對無粘結筋應力增量的影響，令μpym為跨中板帶單位板寬的綜合配筋指標β0等基本參數相同的情況下分別配有HPB300、HRB335、HRB500和HRB600非預應力筋的跨中板帶與配有HRB400非預應力筋的跨中板帶在正常使用極限狀態下無粘結筋應力增量的比值.則根據有限元模擬計算結果，可得到與非預應力筋抗拉屈服強度fy對應的μpym關系圖，見圖6．

圖6 μpym與fy關系

由圖6可知，不同非預應力筋鋼種對柱支承雙向板正常使用極限狀態無粘結筋應力增量的影響較為明顯，且隨著非預應力筋強度等級的提高無粘結筋應力增量有所提高.取圖6中數據點的下包線作為非預應力筋鋼種影響系數μpym的方程曲線，則

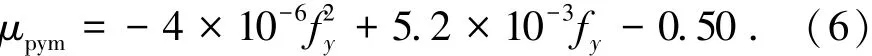
則配置任一非預應力筋鋼種的柱支承雙向板柱上板帶無粘結筋在正常使用極限狀態下的應力增量Δσpym為

4.3 承載能力極限狀態無粘結筋應力計算

4.3.1 柱上板帶無粘結筋應力增量計算

以控制截面受壓區外邊緣混凝達到極限壓應變作為柱支承雙向板的承載能力極限狀態的標志，基于仿真結果，可得到柱上板帶中無粘結筋在承載能力極限狀態下的應力增量Δσpuz隨綜合配筋指標β0的變化關系．以配有HRB400級非預應力筋的雙向板模型計算結果為基礎，其柱上板帶在承載能力極限狀態下的β0-Δσpuz計算結果見圖7．

由圖7可知，在承載極限狀態下，隨著柱上板帶β0的增大，無粘結筋應力增量呈下降趨勢，這是由于隨著綜合配筋指標的增加，雙向板的塑性轉動能力也隨之降低．取圖7中數據點的下包線作為非預應力筋配筋為HRB400的柱支承預應力混凝土雙向板中無粘結筋應力增量ΔσpuzHRB400的公式擬合曲線，則

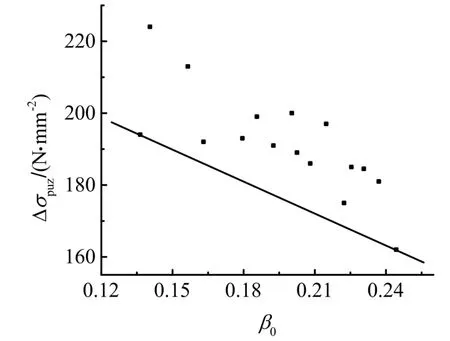
圖7 Δσpuz與β0的擬合曲線

令μpuz為在單位板寬綜合配筋指標等基本參數相同的情況下分別配有HPB300、HRB335、HRB500和HRB600非預應力筋的柱上板帶與配有HRB400非預應力筋的柱上板帶在承載能力極限狀態下無粘結筋應力增量的比值.則根據有限元模擬計算結果，可得到與非預應力筋抗拉屈服強度fy對應的μpuz關系圖，見圖8.

圖8 μpuz與fy關系

由圖8可知，不同非預應力筋鋼種對柱上板帶影響系數μpuz產生影響，隨著非預應力筋強度等級的提高μpuz有所提高．取圖8中數據點的下包線作為非預應力筋鋼種影響系數μpuz的方程曲線，則

結合式（8）、（9），并仿照中國JGJ92—2004《無粘結預應力混凝土結構技術規程》修訂稿中考慮預應力混凝土連續梁加載跨數對無粘結筋極限應力增量影響的方法，在承載使用極限狀態下，配置任一非預應力筋鋼種的柱上板帶無粘結筋應力增量Δσpuz為

式中：lz1為兩錨固端間無粘結預應力筋總長；lz2為與lz1相關的由活荷載最不利布置圖確定的荷載跨長度之和．

4.3.2 跨中板帶無粘結筋應力增量計算

基于仿真結果，得到跨中板帶中無粘結筋在承載能力極限狀態下的應力增量Δσpum隨綜合配筋指標β0的變化關系．以配有HRB400級非預應力筋的雙向板模型計算結果為基礎，其跨中板帶在承載能力極限狀態下的β0-Δσpum計算結果見圖9．

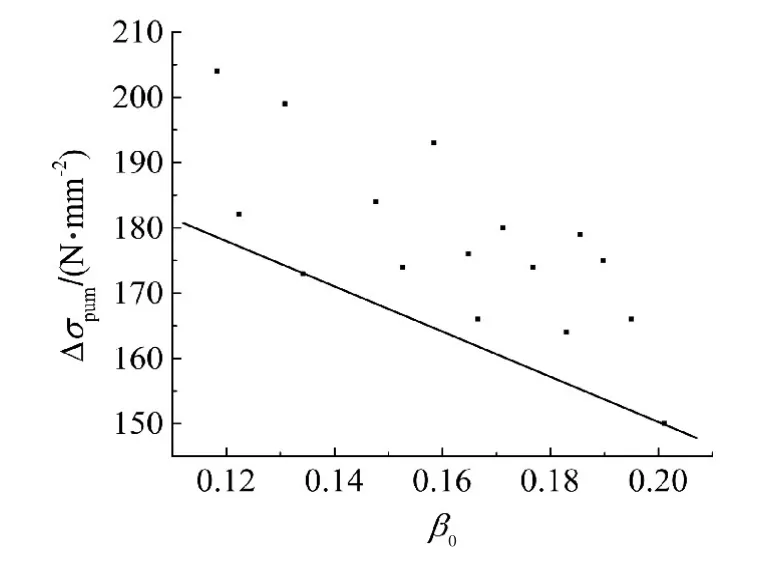
圖9 Δσpum與β0的擬合曲線

由圖9可知，在承載極限狀態下，隨著跨中板帶β0的增大，無粘結筋應力增量呈下降趨勢，這是由于隨著綜合配筋指標的增加，雙向板的塑性轉動能力也隨之降低.取圖9中數據點的下包線作為非預應力筋配筋為HRB400的跨中板帶無粘結筋應力增量ΔσpumHRB400的公式擬合曲線，得

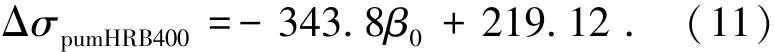
令μpum為在單位板寬綜合配筋指標等基本參數相同的情況下分別配有HPB300、HRB335、HRB500和HRB600非預應力筋的跨中板帶與配有HRB400非預應力筋的跨中板帶在承載能力極限狀態下無粘結筋應力增量的比值.則根據有限元模擬計算結果，可得到與非預應力筋抗拉屈服強度fy對應的μpum關系圖，見圖10．

圖10 μpum與fy關系

由圖10可知，不同非預應力筋鋼種對跨中板帶影響系數μpum產生影響，隨著非預應力筋強度等級的提高μpum有所提高．取圖10中數據點的下包線作為非預應力筋鋼種影響系數μpum的方程曲線，則

仿效式（10），在承載使用極限狀態下，配置任一非預應力筋鋼種的跨中板帶無粘結筋應力增量Δσpu為

5.1 參數分析

5.1.1 跨高比的影響

由于柱支承無粘結預應力混凝土雙向板的常用跨高比范圍為1／40～1／45，相差不大，且經分析在此范圍內跨高比對預應力混凝土雙向板彎矩調幅影響不大，因此暫不考慮跨高比的影響.

5.1.2 綜合配筋指標的影響

根據有限元分析結果，得到圖11所示的等代框架梁支座控制截面彎矩調幅系數α隨綜合配筋指標β0變化的關系圖．從圖11可知，隨著綜合配筋指標β0的增加彎矩調幅系數α隨之減小．雙向板調幅幅度大約在0.1～0.35，因此若將彎矩調幅系數α取為常值將產生一定的誤差．

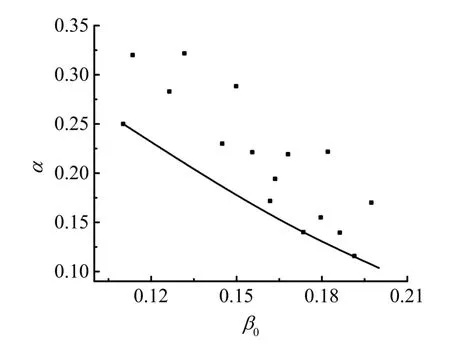
圖11 α與β0關系

5.1.3 預應力度的影響

為進一步考察在綜合配筋指標一定的情況下預應力度λ對彎矩調幅系數的影響，對原無粘結預應力混凝土柱支承雙向板模型中的預應力筋與非預應力筋用量進行了調整，使之在綜合配筋指標β0不變的情況下，將預應力度分別控制在0.5、0.6、0.7、0.8四個等級進行分析．不同綜合配筋指標β0下雙向板支座截面彎矩調幅系數α隨λ的變化曲線見圖12．可看出，在β0相同的情況下改變預應力度對雙向板彎矩調幅影響不大．雖然預應力度的增加導致彎矩調幅系數變小，但總體上彎矩調幅系數α變化不明顯，因此在彎矩調幅系數計算公式中不計入預應力度的影響．

圖12 α與λ關系

5 雙向板內力重分布設計

5.1.4 非預應力筋鋼種的影響

令μsz為在單位板跨綜合配筋指標等基本參數相同的情況下分別配有HPB300、HRB335、HRB500和HRB600級非預應力筋的雙向板與配有HRB400級非預應力筋的雙向板彎矩調幅系數的比值.則根據有限元模擬計算結果，可得到與非預應力筋抗拉屈服強度fy對應的μsz關系曲線見圖13．不同非預應力筋鋼種對彎矩調幅系數α的影響較為明顯，且隨著非預應力筋強度等級的提高呈下降趨勢．

圖13 μsz與fy關系

5.2 彎矩調幅系數計算公式的建立

綜上所述，影響無粘結預應力混凝土雙向板彎矩調幅系數的主要參數應為綜合配筋指標β0和非預應力筋鋼種.以配有HRB400級非預應力筋的柱支承無粘結預應力混凝土雙向板彎矩調幅系數αzHRB400的函數表達式做為基本公式，由圖11可得αzHRB400函數表達式（14）.這里需要指出，考慮到若調幅過高將造成雙向板產生過度塑性變形，難以保證正常使用階段的撓度及裂縫寬度限制要求，因此建議最大調幅幅度為0.30.

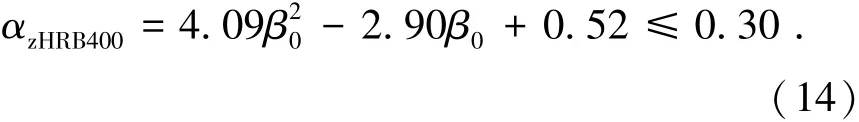
對配有任一強度等級非預應力筋的柱支承無粘結預應力混凝土雙向板彎矩調幅系數α可表達為非預應力筋鋼種影響系數μsz與基本計算式αzHRB400的乘積形式：

取圖13中數據的下包線作為非預應力筋鋼種影響系數μsz的方程曲線：

6 結 論

1）九柱四板格ABAQUS有限元模型分析結果表明：在綜合配筋指標和預應力度一定的條件下，正常使用階段和承載能力極限狀態無粘結筋應力增量隨非預應力筋屈服強度的提高而增大，而支座控制截面的彎矩調幅系數隨非預應力筋屈服強度的提高而減小.

2）建立了正常使用階段和承載能力極限狀態下柱支承預應力混凝土雙向板柱上板帶和跨中板帶無粘結筋應力增量公式.

3）建立了柱支承無粘結預應力混凝土雙向板等效框架板帶支座控制截面彎矩調幅系數計算公式.

［1］鄭文忠，解恒燕.預應力混凝土結構設計中應注意的若干問題［J］.建筑結構，2007，37（6）：97-98.

［2］孟少平，吳京，呂志濤.預應力混凝土井式梁和雙向板中的次彎矩［J］.建筑結構，1998（12）：37-39.

［3］金偉良，呂志濤.無粘結預應力筋的極限應力［J］.浙江大學學報：自然科學版，2000，34（4）：393-397.

［4］潘立.雙向預應力平板中無粘結預應力鋼筋應力的計算［J］.工業建筑，1989（8）：9-13.

［5］堯國皇，陳宜言，孫占琦，等.ABAQUS軟件在建筑結構構件和節點分析中的應用［J］.廣東土木與建筑，2009（9）：6-9.

［6］司炳君，孫治國，艾慶華.Solid65單元在混凝土結構有限元分析中的應用［J］.工業建筑，2007，37（1）：87-92.

［7］王素裹，韓小雷，季靜.ABAQUS顯式分析方法在鋼筋混凝土結構中的應用［J］.科學技術與工程，2009，9（16）：4688-4692.

［8］SAENZ L P.Discussion of equation for the stress-strain curves of concrete by desayi and krishnan［J］.ACI Journal，1964，61（9）：381-393.

［9］過鎮海.混凝土的強度和變形-試驗基礎和本構關系［M］.北京：清華大學出版社，1997.

［10］江見鯨，陸新征，葉列平.混凝土結構有限元分析［M］.北京：清華大學出版社，2005.

［11］LUBLINER J，OLIVER J，OLLER S，et al.A plasticdamagemodel for concrete.international［J］.Journal of Solids and Structures，1989，25（3）：299-326.

［12］DRUCKER D C，PRAGER W.Soil mechanics and plastic analysis or limit design［J］.Quarterly of Applied Mathematics，1952，10：157-165.

［13］樓鐵炯.無粘結預應力梁的有限元建模與性能分析研究［D］.杭州：浙江大學，2005.

［14］陶學康，王逸.無粘結部分預應力帶狀布束的九柱四板荷載試驗［J］.建筑結構，1995，25（7）：38-42.

［15］GUIGLIA M，DEBERNARDI P G，TALIANO M. Calculation of the ultimate stress of unbonded tendons in prestressed concrete members considering the rotation capacity［J］.Magazine of Concrete Research，2012，65（1）：14-26.

［16］LUO Y H，DURRANIA J.Equivalent beam model for flat-slab buildingsⅠ：interior connections［J］.ACI Structural Journal，1995，92（1）：115-124.

［17］HE Zhiqi，LIU Zhao.Stresses in external and internal unbonded tendons：unified methodology and design equations［J］.Journal of Structural Engineering，2010，136（9）：1055-1065.

［18］NAAMAN A E，ALKHAIRIF M.Stress at ultimate in unbonded prestressing tendons：part1-evalutaion of the state-of-art［J］.ACI Structural Journal，1991，88（5）：641-651.

（編輯 趙麗瑩）

Internal force redistribution of unbonded prestressed concrete flat plates

WANG Xiaodong1，2，3，ZHENGWenzhong1，2，WANG Ying1，2
（1.Key Lab of Structures Dynamic Behavior and Control（Harbin Institute of Technology），Ministry of Education，150090 Harbin，China；2.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China；3.School of Civil Engineering，Harbin University of Science and Technology，150001 Harbin，China）

To explore the rule of stress increment in unbonded tendons and design method of moment redistribution，the finite element was modeled by ABAQUS soft-ware for unbonded prestressed concrete flat plates.The plateswere divided into the column strips and the middle ones.Stress increment in tendons and moment redistribution coefficient of unbonded prestressed concrete flat plates were studied，which are influenced by the combined reinforcement index and grade of non-prestressing reinforcement.It is shown that the stress increment in tendons increases at the serviceability and ultimate limit states and moment redistribution coefficient in critical section of support reduceswith the higher yield strength of non-prestressing reinforcements in flat plates.Then expressions of stress increment in tendons and moment redistribution coefficient in prestressed concrete flat plateswere developed，in which the combined reinforcement index and grade of non-prestressing reinforcementwere considered.

prestressed concrete；flat plate；finite element；stress increment in tendon；moment redistribution coefficient

TU378.1

A

0367-6234（2014）12-0001-07

2014-04-11.

國家自然科學基金資助（51378146）；國家教育部長江學者獎勵計劃（2009-37）；教育部博士點基金（20132302110064）.

王曉東（1979—）男，博士研究生；鄭文忠（1965—）男，博士生導師，長江學者特聘教授.

鄭文忠，hitwzzheng＠163.com.