潛艇浮筏隔振系統的半主動變結構控制

趙成（蘇州市職業大學自動化系，江蘇蘇州215104）

潛艇浮筏隔振系統的半主動變結構控制

趙成
（蘇州市職業大學自動化系，江蘇蘇州215104）

對帶有電流變液智能阻尼器的雙層浮筏隔振系統設計了一種半主動輸出反饋變結構控制器。根據滑模運動方程穩定的Hurwitz判據選擇滑模面矩陣。半主動控制條件限制電流變阻尼器可控阻尼力對隔振系統做負功，耗散振動能量。仿真分析了浮筏隔振系統在掃頻激勵信號下的力傳遞率及在雙頻激勵信號下的輸入力與輸出力曲線。同時還仿真分析了雙頻激勵信號作用下半主動靜態輸出反饋變結構控制下的雙層浮筏隔振系統在系統參數出現攝動時的魯棒性。仿真結果表明：半主動輸出反饋變結構控制下的浮筏隔振系統的減振效果要遠好于最優被動阻尼系統，對系統參數攝動也具有很強的魯棒性。

半主動；變結構控制；浮筏；隔振系統

1 引言

浮筏是應用于船艦上的一種新型隔振降噪裝置，它是把船艦中的馬達、風機等多臺動力設備彈性地安裝在一個公共的筏架上，再將筏架彈性地安裝在船身基礎上。實際上，浮筏就是一種特殊的隔振系統，其機理是利用浮筏裝置中彈性元件的阻尼和中間質量的設計來控制并衰減振動能量，使船艦表殼的振動減小。

從六十年代起，國內外許多學者在船艦的減振降噪方面進行了大量研究，提出了許多種方法并發表了相關論文[1-2]。近三十多年來，越來越多從事船艦設計的專家認為，船艦的減振降噪是一個急需解決的重要問題。降低艙室的振動和噪聲不僅可以改善船艦上人員的居住和工作環境，重要的是能夠保障船艦上精密儀器設備的正常運行，保證船艦的正常行使，特別是對于軍用艦艇來說，能夠增加其航行的穩定性和隱蔽性，提高戰斗力。因此，改善船艦上浮筏隔振系統的減振性能是一個十分重要的問題。

半主動隔振系統在控制品質上接近于全主動隔振系統[3]，且控制較為簡單，能耗小。電流變阻尼器能夠根據所加控制電壓的不同而改變其阻尼力，轉變過程迅速且可靠。本文將電流變阻尼器應用于浮筏隔振系統，同時考慮到電流變阻尼器存在的非線性特性及浮筏隔振系統模型參數的變化，有必要采取魯棒控制策略[4-5]。常用的魯棒控制策略有自適應控制法[6]，變結構方法和H∞方法等。本文將變結構方法用于帶有電流變智能阻尼器的浮筏隔振系統的控制，設計了一種半主動輸出反饋變結構控制器，仿真了系統在掃頻激勵信號下的力傳遞率及在雙頻激勵信號下的輸入力與輸出力曲線，同時還仿真分析了雙頻激勵信號作用下半主動靜態輸出反饋變結構控制下的雙層浮筏隔振系統在系統參數出現攝動時的魯棒性，對控制效果進行了仿真評價。仿真結果表明半主動輸出反饋變結構控制下的浮筏隔振系統的減振效果要好于最優被動阻尼系統，對系統參數攝動也具有很強的魯棒性。

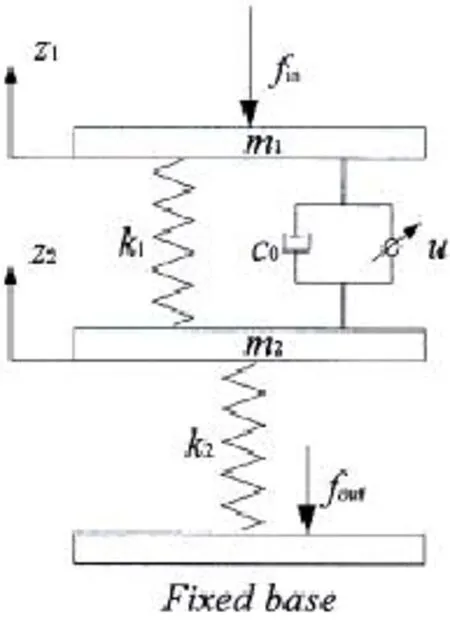
圖1 浮筏隔振系統模型Fig.1 Themodel of floating raft isolation system

2 電流變智能阻尼器浮筏隔振系統

2.1 浮筏隔振系統模型

圖1所示為帶有電流變智能阻尼器的雙層浮筏隔振系統模型。其中：m1、m2分別為上層質量、中間質量；k1、k2分別為初級隔振彈簧剛度、次級隔振彈簧剛度；z1、z2分別為上層質量受振后產生的位移、中間質量受振后產生的位移；fin為施加在上層質量上的豎直方向的激振力；fout為基座受到的振動力。

浮筏系統動力學方程為：

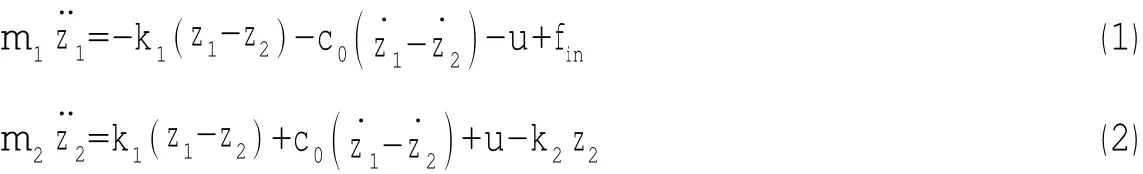
利用加速度傳感器分別測量上層質量的加速度z¨1與中間質量的加速度z¨2，通過高通濾波器對低頻噪聲信號過濾，然后分別積分得到相應的絕對速度z˙1和z˙2；采用位移傳感器測量相對位移z1-z2。

其中：

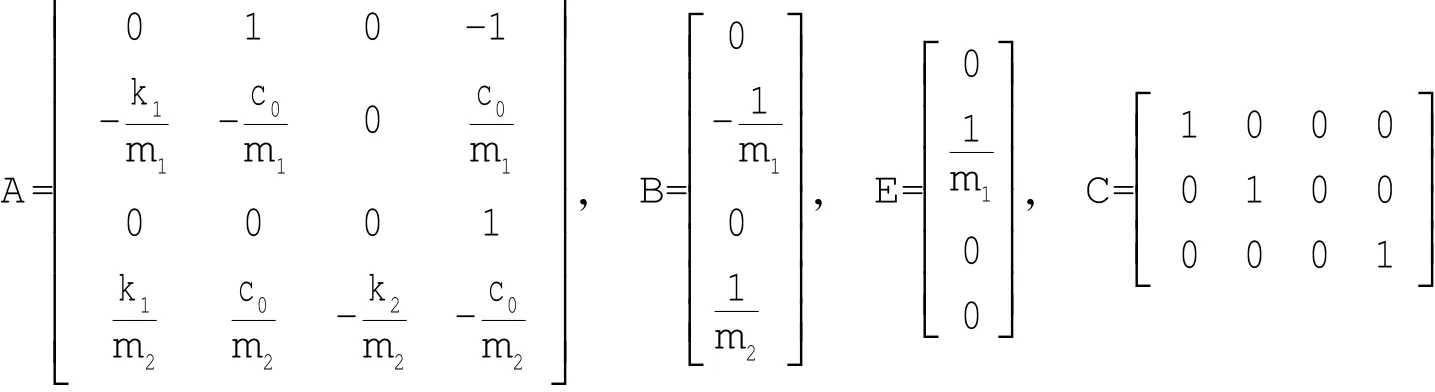
圖2 力隔振臺架Fig.2 Diagram of force isolation

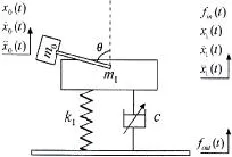
圖3 力隔振臺架激振力模型Fig.3 Mechanicalmodel of exciting force

2.2 浮筏隔振臺架

本文針對動力設備振動力傳遞控制研究的要求，設計了相應的力隔振臺架，如圖2所示。

力隔振臺架由激振器A1、上層板A5、初級隔振彈簧A6、中層板A7和次級隔振彈簧A8構成，并通過4個限位桿A3豎直地安裝在基礎之上，如圖2所示。電流變阻尼器B3的活塞桿和外殼分別安裝在上層、中層板的中間位置。激振器通過M形A2平臺安裝在上層板上，二者共同構成上層質量。中層板加上一定質量的配重，構成中間質量（圖中略）。上層板和中層板上均裝有線性軸承A4，以減小摩擦力。由于限位桿的作用，力隔振臺架只能在豎直方向運動，因此構成一個典型的二自由度系統。如果將中間質量與基礎緊固，系統就成為一個典型的單自由度系統。

力隔振臺架上安裝了多種傳感器，可以測量各種物理量。其中，加速度傳感器B1測量上層質量的豎直加速度，加速度傳感器B6測量中間質量的豎直加速度。力傳感器B5測量電流變阻尼器的輸出力。位移傳感器B2測量上層質量的絕對位移，位移傳感器B7測量中間質量的絕對位移，位移傳感器B4測量上層質量和中間質量的相對位移。

2.3 激振力分析

為克服現有力隔振臺架單振動電機引起的非豎直方向的振動力和位移[7]，本文設計的激振器由兩臺振動電動機組成。振動電動機的軸兩端分別安裝相同的偏心質量塊。兩臺振動電機通過一對沿軸安裝的齒輪同步運轉。根據同步振動原理，在一臺變頻器的驅動下，兩臺振動電動機始終保持方向相反、相位對稱的同步轉動。4塊偏心質量塊產生的偏心力，在水平方向相互抵消，在豎直方向疊加。因此，激振器只提供豎直方向上的激振力，從而理論分析也大大簡化。

圖3中，m0為單個偏心質量塊的質量。假設變頻器控制電動機做勻速轉動，角速度為ω。根據圖3，在t時刻m0和m1在豎直方向的相對速度關系如下：

而

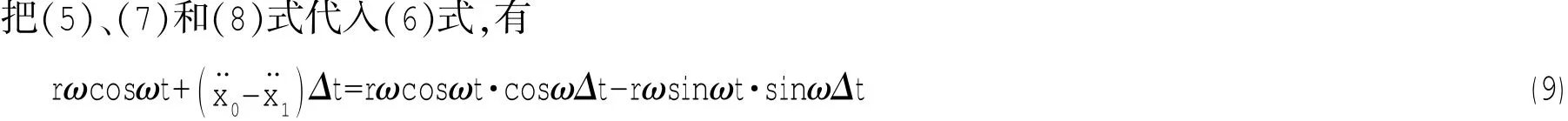
忽略偏振質量塊的重量影響，則可以認為偏振質量塊m0的豎直方向的加速度源自于上層質量體m1對它的作用力的豎直方向上的分量。根據牛頓第三定律，上層質量m1受到的豎直方向的激振力為：

（11）式表明，fint（）實際上等于偏心力的豎直分量減去偏心質量塊隨上層質量一同運動的慣性力。

2.4 電流變阻尼器模型

根據Bingham模型，電流變阻尼器的阻尼力可表達為：F=c0x˙+u sgn）；式中c0為零電場粘性阻尼系數；u為可控屈服阻尼力；x˙為活塞與缸體的相對速度。sgn（）為符號函數。根據實驗數據，擬合出可控阻尼力u與外加電壓的關系式：

式中：U為電壓，a0，a1，a2均為試驗確定的常數。試驗數據確定的常數：c0=1 013.4 Ns/m，a0=10.23 N，a1= 6.38 N·kV，a2=2.59 N·kV2。

圖4給出了不同電壓作用下阻尼力—活塞速度關系曲線。試驗中活塞運動速度為15～100mm/s、激勵幅值為60mm。增加電壓，阻尼力增加。由圖4可見，仿真結果與試驗結果非常接近，表明上述阻尼器力學模型是合理的。

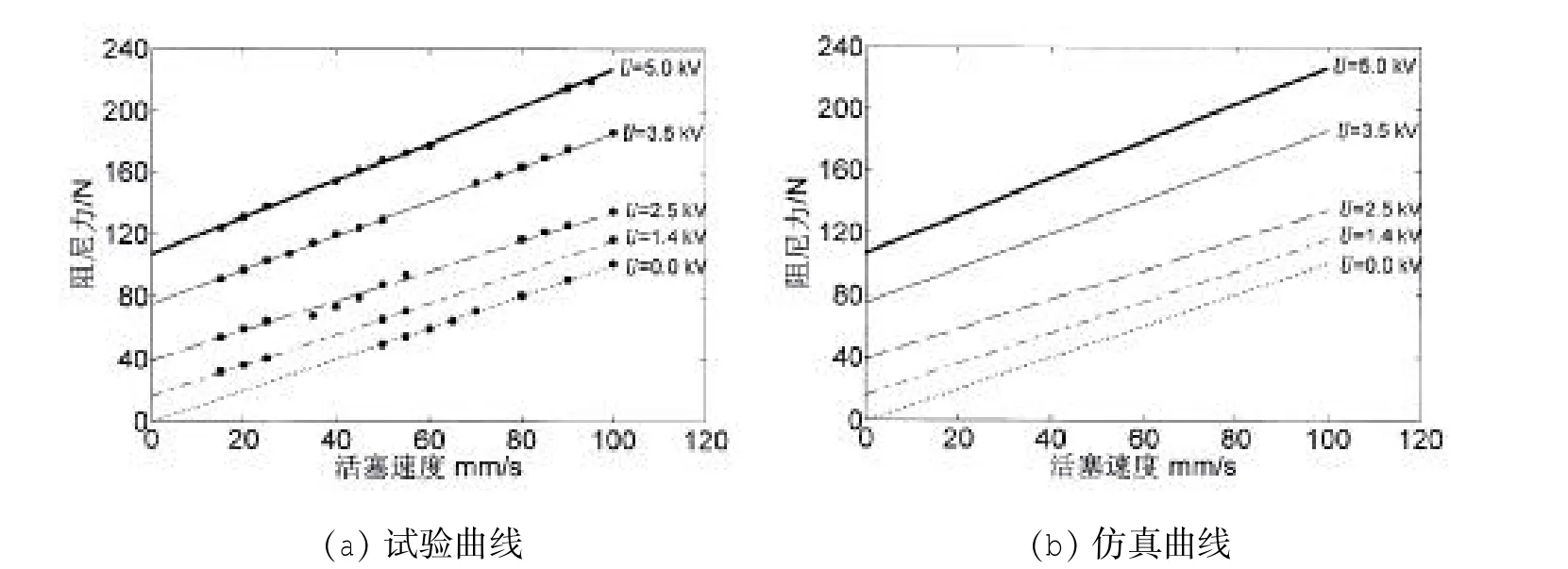
圖4 不同電壓作用下阻尼力—活塞速度關系曲線Fig.4 Damping force versus piston velocity at various voltages

3 浮筏隔振系統半主動輸出反饋變結構控制器設計

3.1 輸出反饋變結構控制設計條件

給定以下線性時不變系統：

其中：狀態x∈Rn，控制u∈Rm，輸出y∈Rl。假設A，B（）可控，A，C（）可觀，且rank CB（）=m。選擇滑模面：

根據等效控制設計方法[8]，在滑模面上有：

由（13）、（14）和（15）式及（16）式可得：

由（17）式得到等效控制：

將（18）式代入（13）式，得到滑動模態運動方程：

從（18）、（19）式可以看出，要使等效控制和滑動模態存在，就必須要求GCB（）-1存在，即：

由（20）式可得：

上式要求傳感器的數量至少要等于執行器的數量。

3.2 滑模面的設計

由線性系統理論知，由于A，B（）可控，則可通過線性變換將（13）、（14）式變為以下簡約型：

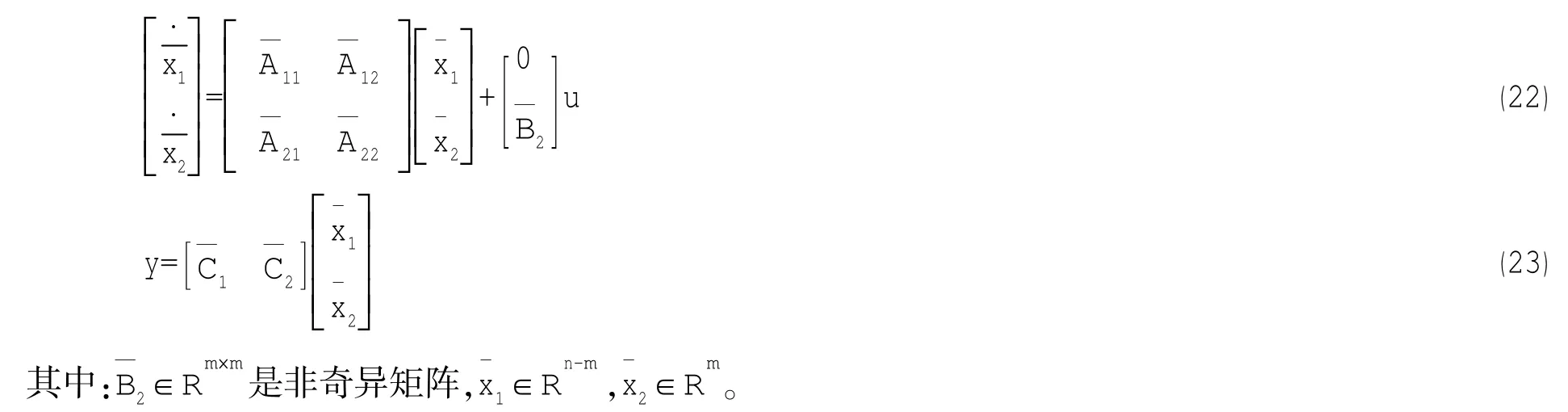
在滑模面上有：

由于要求（GCB）-1存在，所以也存在。

由（24）式得：

必須選擇適當的矩陣G使得滑動模態運動方程（26）穩定。令：

可以用一般的線性系統輸出反饋特征結構來設計H[9]，然后再從（27）式解出G。G存在的充分必要條件是[10]：

3.3 輸出反饋變結構控制器的設計

對本文所研究的電流變智能半主動浮筏隔振系統狀態方程式（3）和（4），定義滑模面：

式中：G=g1g2g3［、是滑模面矩陣。

在進行滑模面的設計時，忽略（3）式中的外界激勵fin，而在控制器的設計中加以考慮[11]。由于A，B（）可控，則可通過線性變換：

將（3）、（4）式變為如（22）、（23）式所示的簡約型，各分塊陣為：

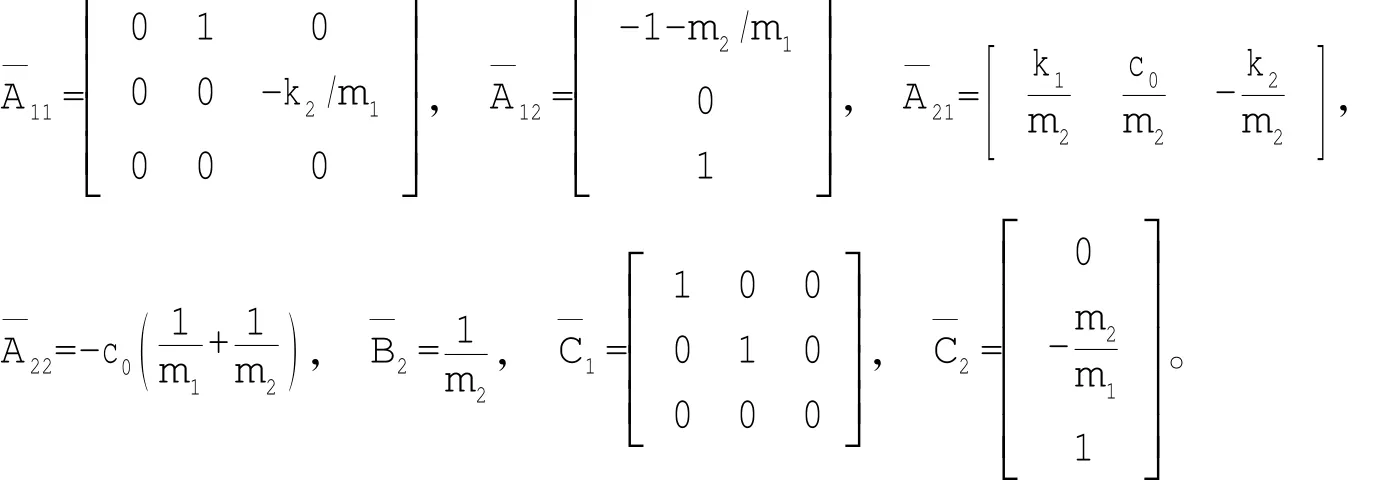
將降維滑動模態運動方程表示為（28）式的形式，式中：H=［h1h2h3、。

滑動模態運動方程（28）式的特征多項式為：

由滑動模態運動方程式（28）的Hurwitz穩定判據可以得到：

在（39）、（40）式的約束條件下，簡單選取

本文所研究的浮筏隔振系統中，上層質量為中間質量的二倍。即：

由（42）、（43）式和（44）式得滑模面矩陣為：

由（43）、（45）式知，條件式（33）是成立的。

選取如下形式的控制律：

式中：k＞0。

由滑模可達性條件STS˙＜0有

從（47）式可以看出，如果CTGTGCA≤0，則選擇N=0就可以使滑模可達性條件得到滿足。

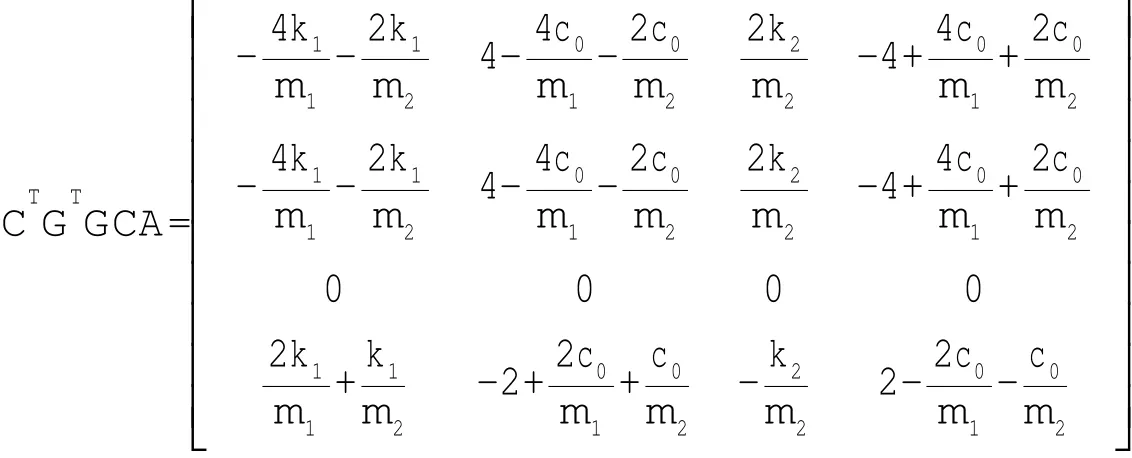
對于本文研究的電流變智能半主動浮筏隔振系統，由仿真實驗中給出的系統參數可知是半負定的，所以我們選擇

在控制律的表達式（46）中包含了前饋補償，即：-GCB（）-1GCEfin。對于我們研究的實際的減振系統，上層質量的加速度、上層質量與中間質量的相對位移以及電流變阻尼器的阻尼力是可以檢測得到的，根據浮筏系統動力學方程（1），激勵力fin是容易通過下式確定的。

（49）式中的F為力傳感器測量得到的電流變阻尼器的阻尼力。

由（48）式，控制律（46）式變為：

3.4 飽和約束條件

由于最大可控阻尼力受到電流變阻尼器具體的結構形式限制，只能是一個有限值。所以在輸出反饋變結構控制電流變阻尼器隔振系統中引入飽和非線性控制環節，表示為：

3.5 半主動控制條件

根據圖1，fout=k2z2為基座受到的振動力，即浮筏隔振系統的輸出力。對于我們所研究的雙層浮筏隔振系統，要求電流變阻尼器可控屈服阻尼力只能對隔振系統做負功，耗散中間質量體m2的振動能量，相應的半主動控制策略為：

在確定了可控屈服阻尼力后，結合（12）式所確定的電流變阻尼器的外加電壓為：

綜合上面的分析，電流變阻尼器浮筏隔振系統控制框圖如圖5所示。

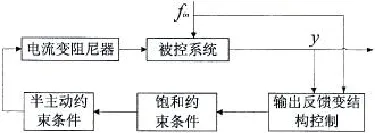
圖5 控制系統框圖Fig.5 Controlblock diagram of semi-active floating raft isolation system

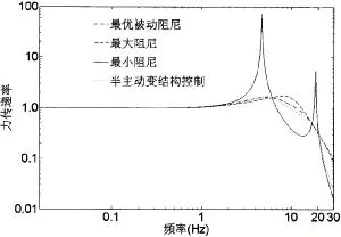
圖6 掃頻信號激勵下隔振系統力傳遞率Fig.6 Force transmissibility of semi-active floating raft isolation system to sweep-frequency signal

4 仿真實驗

在上述控制律基礎上，運用Matlab7.0對系統進行仿真，仿真實驗中的參數如下：

m0=3.2 kg，m1=32 kg，m2=16 kg，

c0=1 013.4 N S/M，r=0.002m，

k1=33 000 N/m,k2=185 000 N/m，

copt=1 453 N s/m，Umax=5 kV，

a0=10.23 N，a1=6.38 N·kV，

a2=2.59 N·kV2。

備注：copt為最優被動阻尼。

4.1 掃頻信號輸入

輸入信號為頻率0-30 Hz的掃頻信號，掃頻時間為30 s。

圖6為單個掃頻信號激勵下隔振系統力傳遞率曲線。為了更好地說明隔振系統在半主動輸出反饋變結構控制下的減振效果，圖中同時給出了隔振系統在無控制作用的最小阻尼、最優被動阻尼及最大阻尼情況下的力傳遞率。從圖6中可以看出，半主動輸出反饋變結構控制下的雙層力隔振系統的控制效果要好于最優被動系統，它減低了基座受力，提高了船艦行使的安全性。

4.2 雙頻激勵

激勵信號由兩個單頻信號合成得到，信號的形式為：2

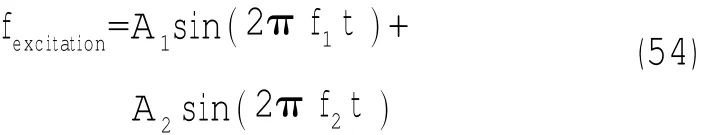
隔振系統的一階共振頻率與二階共振頻率約為5 Hz，16 Hz。從（11）式可以看出，在同一個輸入激勵信號作用下，對無控制作用的最優被動阻尼系統與半主動輸出反饋變結構控制下的隔振系統來說，由于所產生的上層質量的加速度是不同的，所以對兩個系統所產生的輸入激勵力是不同的，因而不能單獨以兩個不同系統在同一個輸入激勵信號作用下的輸出力響應曲線來判斷各個系統的隔振效果。為此，本文仿真給出了無控制作用的最優被動阻尼系統與半主動輸出反饋變結構控制下的隔振系統在以下雙頻激勵信號下的輸入力及輸出力曲線，持續時間都為2 s。

圖7為雙頻信號激勵下最優被動阻尼系統與半主動輸出反饋變結構控制下的隔振系統的輸入力及輸出力響應曲線。圖8為系統參數發生攝動時（Δm1=-0.1m1，Δk1=-0.1k1及Δk2=-0.1k2）雙頻信號激勵下最優被動阻尼系統與半主動輸出反饋變結構控制下的隔振系統的輸入力及輸出力響應曲線。從圖7及圖8中可以看出，無論系統參數是否發生攝動，相對于最優被動阻尼系統的輸出力比輸入力幅度的降低，半主動輸出反饋變結構控制下的隔振系統的輸出力比輸入力有更大幅度的減小，為此說明半主動輸出反饋變結構控制下的隔振系統減振效果要明顯好于最優被動隔振系統。

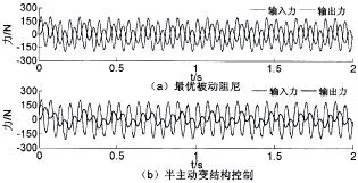
圖7 雙頻信號激勵下的輸入力及輸出力響應曲線Fig.7 Input force and output force response to dual-frequency signal excitation

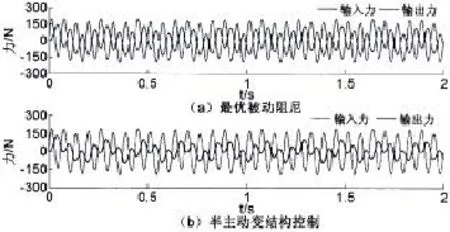
圖8 系統參數攝動時（Δm1=-0.1m1，Δk1=-0.1k1及Δk2=-0.1k2）雙頻信號激勵下的輸入力及輸出力響應曲線Fig.8 Input force and output force response to dual-frequency signal excitation with parameter uncertainties(Δm1=-0.1m1, Δk1=-0.1k1andΔk2=-0.1k2)

5 結語

運用變結構控制方法設計了帶有電流變阻尼器的雙層浮筏隔振系統的半主動輸出反饋變結構控制器。仿真分析了浮筏隔振系統在掃頻激勵信號下的力傳遞率及在雙頻激勵信號下的輸入力與輸出力曲線。同時還仿真分析了雙頻激勵信號作用下半主動靜態輸出反饋變結構控制下的雙層浮筏隔振系統在系統參數出現攝動時的魯棒性。從仿真結果看，無論系統參數是否發生攝動，半主動輸出反饋變結構控制下的浮筏隔振系統的隔振效果要好于最優被動系統，使基座受力得到明顯降低，提高了船艦行使的安全性。

參考文獻：

[1]許樹浩,桂洪斌.浮筏系統隔振性能的功率流評價指標[J].船舶力學,2012,16(5):567-572. Xu Shuhao,Cui Hongbin.Power flow estimation of float raft isolation system[J].Journal of Ship Mechanics,2012,16(5): 567-572.

[2]張樹楨,陳前.柔性浮筏隔振系統的理論建模與仿真研究[J].船舶力學,2012,16(10):1187-1198. Zhang Shuzhen,Chen Qian.Modeling and simulation research on flexible floating raft isolation system[J].Journal of Ship Mechanics,2012,16(10):1187-1198.

[3]Choi SB,Kim W K.Vibration control of a semi-active suspension featuring electrorheological fluid dampers[J].Journal of Sound and Vibration,2000,234(3):537-546.

[4]張孝祖,武鵬,黃少華.基于模糊魯棒控制的車輛半主動懸架性能分析[J].農業機械學報,2006,37(5):1-4.

[5]方敏,史明光,陳無畏.汽車主動懸架多目標H2/H∞混合控制[J].農業機械學報,2005,36(3):4-7.

[6]Youn I,Hac A.Semi-active suspension with adaptive capability[J].Journal of Sound and Vibration,1995,180(3):475-492.

[7]汪建曉,孟光.磁流變液阻尼器用于振動控制的理論及實驗研究[J].振動與沖擊,2001,20(2):39-45.

[8]Andry A N Jr,Shaprio E Y,Chung JC.Eigenstructure assignment for linear system[J].IEEE Transaction on Aerospace Electronic Systems,1983,19(5):711-729.

[9]Heck B S,Ferri A A.Application of output feedback to variable structure systems[J].Journal of Guidance Control and Dynamics,1989,12(6):932-935.

[10]Elbeheiry EM.Effects of small travel speed variations on active vibration control inmodern vehicles[J].Journal of Sound and Vibration,2002,232(5):857-875.

[11]Yang JN,Wu JC,Li Z.Control of seismic-excited buildings using active variable stiffness systems[J].Engineering Structures,1996,18(8):589-596.

Sem i-active variable structure control for floating raft isolation system

ZHAO Cheng
(Dept of Automation,Suzhou Vocational University,Suzhou 215104,China)

A semi-active output feedback variable structure controller is designed for floating raft isolation system with electro-rheological(ER)damper.Sliding surfacematrix is selected in accordancewith Hurwitz stable judgementof slidingmodemotion equation.The optimal vibration attenuation is guaranteed due to the control rule that damping force only dissipates the vibration energy of isolation system.The force transmissibility under conditions of sweep-frequency signal,input force and output force for the floating raft vibration isolation system under conditions of dual-frequency exciting signal are simulated,respectively.The robustness of the controlmethod with respect to parameter variations is simulated.The simulation results indicate that the performance of floating raft vibration isolation system designed by semi-active output feedback variable structure controlmethod is remarkably better than those of optimally passive damping even if system parameter uncertainties exist.

semi-active;variable structure control;floating raft;isolation system

O328 TB535

A

10.3969/j.issn.1007-7294.2014.11.012

1007-7294（2014）11-1367-10

2014-05-12

國家自然科學基金資助項目（69974024）

趙成（1974），男，博士，E-mail：zhaoch@wxit.edu.cn。