近似模型在非均勻環肋圓柱耐壓殼優化中的應用研究

王 建，龐永杰，程妍雪，楊卓懿，劉 偉

（哈爾濱工程大學 水下智能機器人技術國防科技重點實驗室，哈爾濱150001）

1 引 言

耐壓殼是潛水器的一個至關重要的構件，起著承受水壓力，保障艙室內部各種儀器設備正常工作的作用，同時也為潛水器提供了重要的浮力儲備。對于目前潛水器中常用的環肋圓柱耐壓殼而言，相比于球殼等其他形式的耐壓殼，環肋圓柱耐壓殼具有加工難度低，利于艙室布置，屈服強度和穩定性比較容易滿足等優點。但是，對于大多數環肋圓柱耐壓殼而言，屈服強度要求比較容易滿足，而穩定性則較難滿足。為此設計者們通常使用較大厚度的殼板，以提高耐壓殼的屈曲穩定性能，與此同時，這也導致結構強度的利用率下降和成本的上升。為此，近年來有不少的學者從耐壓殼的自身結構形式和布局著手，研究如何提高環肋圓柱耐壓殼的穩定性。如呂春雷[1]對多種型式的肋骨加強的耐壓圓柱殼的穩定性進行了比較研究；朱邦俊[2]提出了半圓環形肋骨的型式以提高耐壓殼的穩定性能；程妍雪[3-4]、Kukbin Kim[5]對肋骨等間距剛度非均勻的環肋耐壓殼的結構強度性能進行了研究。環肋圓柱殼一階失穩時，沿縱向呈現一個正弦半波，艙段中間處的徑向失穩位移最大[3]。因此，改變原來的圓柱耐壓殼的結構布局，采用不等剛度不等間距分布的肋骨形式，提升艙段中間位置的剛度，將有效地提高殼體的穩定性能。

傳統優化的設計方式，根據分析結果，重復著修改模型、計算和分析的循環，不但將導致工作量的空前加大和難度增加，而且在某些算法上還容易使尋優結果陷入局部最優解[6]。在優化過程中引入近似模型（approximation model）技術則能有效地解決上述問題。近似模型考慮了擬合精度和擬合效率[7]，能代替計算龐大的仿真計算，并且還可避免優化過程中時常出現的數值噪聲和錯誤。因此，本文在潛水器的圓柱耐壓殼設計中，引入非均勻肋骨布置方案，并研究了近似模型技術在其優化設計過程中的應用。

2 非均勻環肋圓柱耐壓殼

目前，大多數的外壓圓柱殼的肋骨截面慣性矩沿圓柱殼的軸線方向是等距均勻分布的[3]。雖然，這樣的結構布局有利于加工，降低加工工藝難度，但是從艙段總體穩定性考慮，這并不很合理。因為環肋耐壓圓柱總體失穩時，縱向形成半個正弦波（除非艙段中央部分的肋骨剛度即肋骨截面的慣性矩相當大)，圓柱殼中央部分的徑向失穩位移最大[3-4]。因此，環肋圓柱耐壓殼的肋骨，若采用非均勻的布置形式，將有效地提高耐壓殼的屈曲穩定性能，提高材料的利用率和降低殼體和潛水器的總體重量。

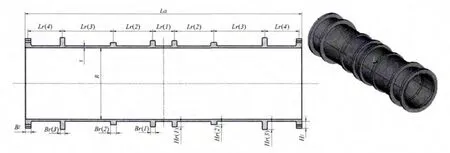
圖1 非均勻環肋圓柱殼剖面圖與三維立體圖Fig.1 The profile and three-dimensional model of the non-uniform ring-frames pressure shell

本文所研究的非均勻環肋圓柱耐壓殼，是指均勻材料的外肋耐壓殼，其肋骨截面的慣性矩非均勻（即肋骨寬、肋骨高尺寸的不同），和肋骨間距的非均勻布置。圖1為本文所討論的非均勻環肋圓柱殼剖面圖與三維立體圖。

文獻[1，4]研究了等間距剛度非均勻環肋圓柱殼的穩定性，并給出了此類環肋圓柱殼總體失穩臨界壓力公式[4]：

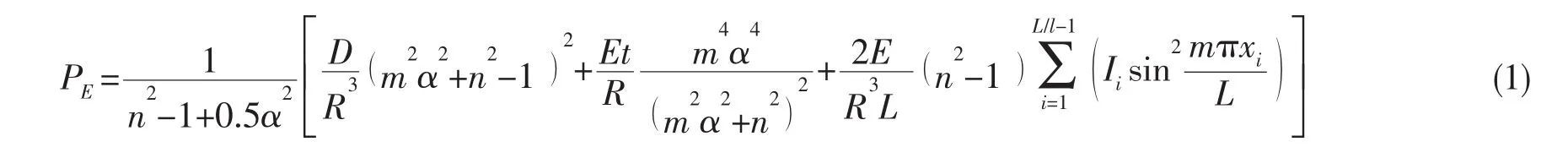
式中：L為兩橫艙壁的間距；m為殼體失穩時沿徑向上形成的半波數，通常m=1；n為殼失穩時沿殼體周上形成的整波數，通常將n=2，3，4分別代入公式，取使臨界壓力最小的值。

由公式（1）可以計算等間距剛度非均勻環肋圓柱殼的穩定性能，并且可知合理地布置肋骨的剛度與間距可以有效地提高耐壓殼的穩定性。但是對于非均勻環肋圓柱殼的屈服、屈曲性能計算分析依舊比較復雜。對于潛水器而言，特別是大潛深的潛水器，其耐壓殼的半徑與厚度比值遠小于20，已屬于中厚度殼體。故，本文依據《潛水系統與潛水器入級建造規范-1996》[8]，采用有限元分析軟件ANSYS計算耐壓殼的結構強度。選取SOLID45單元建立參數化各向同性耐壓殼參數化有限元模型，加載外壓靜水壓力，進行屈服屈曲強度分析。提取柱坐標系下，耐壓殼相鄰肋骨中點處殼板的周向應力σ1，肋骨處殼板的軸向應力σ2，肋骨應力σr，肋骨間殼板屈曲壓力Pcr1，艙段整體總體屈曲壓力Pcr2，作為非均勻環肋耐壓殼的強度校核準則。

3 近似模型

20世紀70年代Schmit等人首次將近似模型的概念引入到結構優化設計中。近似模型技術采用數學模型的方法逼近一組輸入變量與輸出變量的方法，是試驗設計、數理統計和最優化技術的綜合應用[7]。在優化過程中使用近似模型，不但能代替計算量龐大的仿真計算，而且還能避免優化過程中時常出現的數值噪聲和錯誤。故該方法能高效地完成優化任務，并節省大量的計算時間。目前常用的近似模型主要有二階響應面近似模型（response surface model，RSM）和徑向基（radial basis functions，RBF）網絡近似模型，其原理如下。

3.1 響應面近似模型

響應面模型的基本思想是采用低階的多項式對輸入變量和輸出變量回歸分析，運用最小二乘法，構造出精度較高的，能顯式表達近似函數關系。目標函數的響應值y與設計變量x之間的關系如下式所示[6]：

本文在優化中采用的響應面模型為二階響應面模型，其形式如下[6]：

式中：xi為輸入變量，n為輸入變量的個數。a0，bi，cii和dij分別為常數項、一次項、二次項和交叉項的待定系數。

3.2 徑向基（RBF）網絡近似模型

神經網絡是由許多神經元組成的一類適應系統，模擬了人腦的結構和功能，能表述分析復雜的非線性問題和關系。20世紀80年代，Hopfield首次成功地將神經網絡運用于組合優化問題中[9]。徑向基網絡是諸多神經網絡模型中最具有代表性的一種神經網絡模型。

徑向基網絡是一種由輸入層、隱含層和輸出層構成的三層前向性網絡。其基本思想是：以待測點與樣本點之間的歐幾里德距離為自變量，即假設代表一組輸入變量為基函數，通過線性疊加的方式構成徑向基網絡模型。在RBF網絡中，包括輸入層到隱含層非線性變換和隱含層到輸出層線性變換兩個階段，變換的參數包括基函數的中心和方差以及權值。徑向基網絡近似模型，無須任何數學假設，具有黑箱特點，其學習速度快，具有很強的逼近復雜非線性函數能力和極好的泛化能力[9]。

4 基于近似模型非均勻環肋耐壓殼的優化方法

4.1 優化模型

本文討論的非均勻加肋耐壓殼為外肋矩形截面的耐壓殼，其肋骨截面的寬度和高度尺寸均不同，和肋骨間的間距的非均勻，采用左右對稱的結構布置形式。選取圓柱殼內徑R，殼板厚度t，肋骨數N，相鄰兩肋骨間距Lr（i），每根肋骨的高Hr（i），寬 Br（i）（肋骨編號順序，由中間向兩端計數，左右對稱，如圖1所示），法蘭高Hf，法蘭寬Bf為設計變量。以圓柱耐壓殼的重量W為目標函數。以柱坐標系下，耐壓殼相鄰肋骨中點處殼板的周向應力σ1，肋骨處殼板的軸向應力σ2，肋骨應力σr，肋骨間殼板屈曲壓力Pcr1，艙段整體總體屈曲壓力Pcr2的許用值為約束條件。該耐壓殼的設計深度為D=1 000 m，內半徑R=125 mm，艙長L=1 000 mm，重W=22.37 kg。優化模型的相關初始參數如表1所示，各設計變量的約束如表2所示。

表1 優化模型初始參數Tab.1 The initial particular of the model

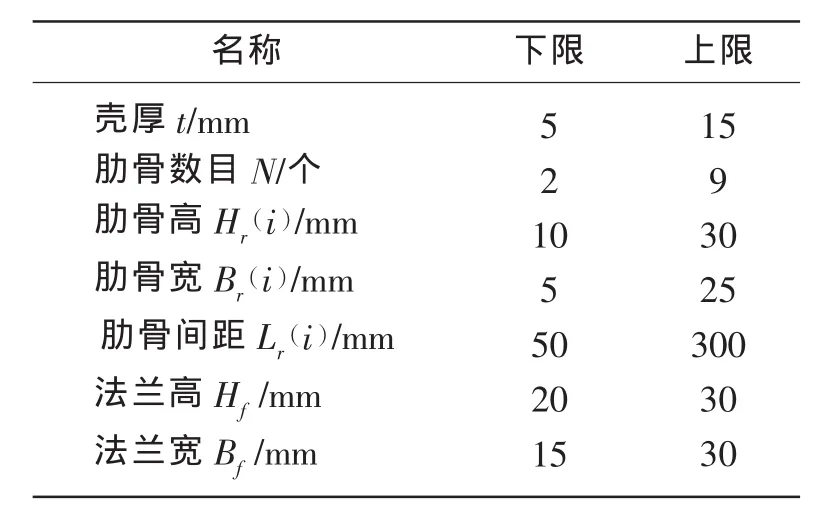
表2 優化模型設計變量約束Tab.2 The bound of the model’s variables

4.2 基于近似模型優化方法

直接將近似模型加載入優化過程中是目前最常用的優化方式。首先在設計空間內運用試驗設計方法安排一定量的仿真計算，對輸入和輸出變量進行分析判斷，以仿真結果為依據建立近似模型。并將檢驗合格滿足精度要求的近似模型加載到優化過程中，利用優化算法對設計變量、約束條件和目標函數的分析，通過近似模型的計算，不斷循環迭代，最終獲得全局最優解。本文在使用近似模型對非均勻環肋圓柱殼進行優化的流程如圖2所示。

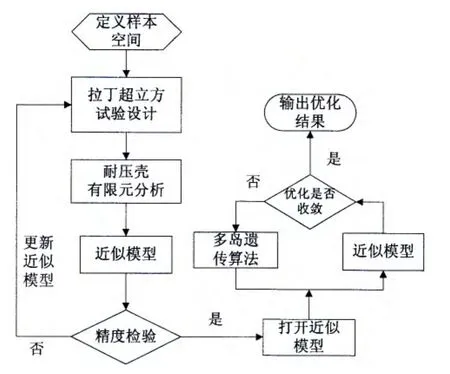
圖2 基于近似模型非均勻環肋圓柱耐壓殼優化流程圖Fig.2 The flow of pressure shell optimization by use approximate model

5 近似模型對比分析及優化實例

5.1 近似模型對比分析

復相關系數R2常被用來衡量近似模型與樣本點相符合的程度[9]。其定義如下：

式中：n為模型驗證的樣本數量，yi為真實相應值，為由近似模型得到的估計值，為真實相應值的均值。R2越接近于1，說明近似模型的可信度就越高。

在本文建立的非均勻加肋圓柱耐壓殼的有限元分析程序中，設計參數相鄰兩肋骨間距Lr（i），每根肋骨的高Hr（i），寬 Br（i）是動態的數組，其維數隨肋骨數變化而變化，故總的設計變量的數量也是變化的，根據研究對象的設計空間，本算例最多時共有23個設計參變量。借助iSIGHT軟件集成ANASYS運用最優拉丁超立方設計（optimal latin hypercube design，Opt LHD）方法分別安排300次、600次、900次、1 200次試驗設計，得到非均勻加肋耐壓殼的各設計參數與重量、應力的樣本響應值。并分別擬合得到耐壓殼的二次多項式RSM近似模型、和RBF近似模型。為預測近似模型的可信度，本文在設計空間內隨機抽取96個點，計算近似模型的復相關系數R2。表3為在各試驗次數下所擬合得到的二次多項式RSM模型和RBF近似模型的復相關系數R2。

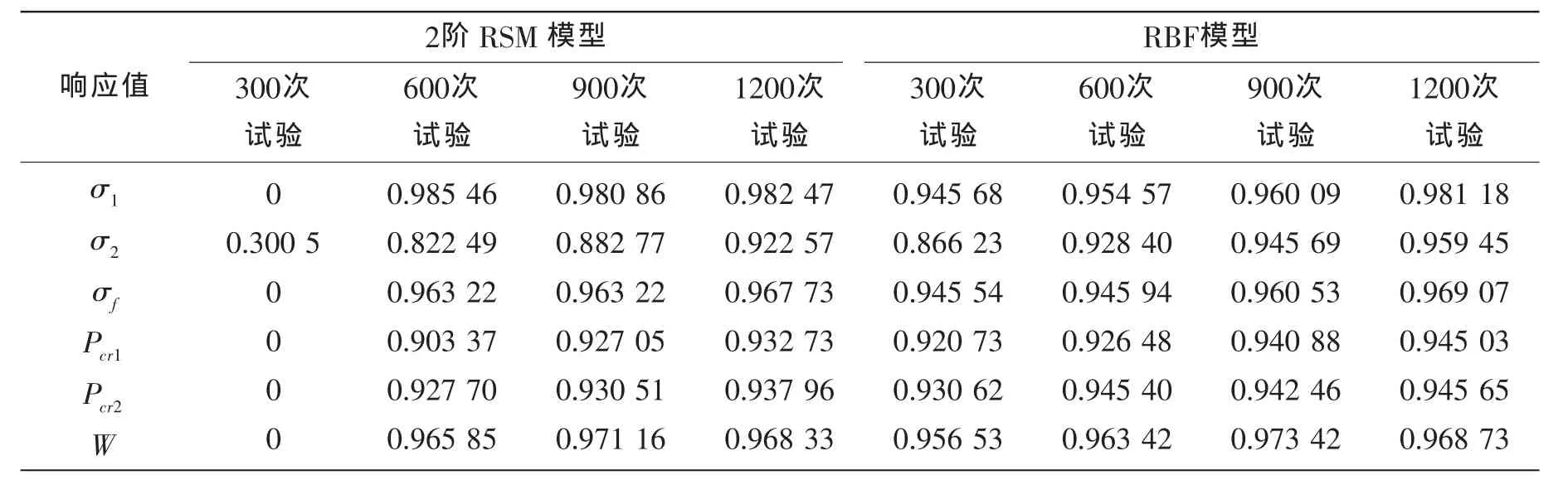
表3 近似模型的精度Tab.3 Precision of approximation model

由表3可知，兩種近似模型對σ2的擬合的質量都不是很好，需要較多的試驗次數才能得到比較滿意的精度；在較低試驗次數下，RBF模型的可信度明顯高于二階RSM模型。在300次試驗設計時RBF模型的可信度除σ2之外，其他的響應值的可信度均大于0.9為可接受的范圍，而二階RSM模型的絕大部分響應值的可信度為0；隨著試驗設計的試驗次數增加，近似模型的可信度也逐步的提高，其中1 200次試驗設計下的近似模型質量最好。所以，當近似模型的可信度不滿足要求是，可以從數量、變量水平、試驗次數以及更換近似模型等方面考慮，以提高近似模型的可信度。

5.2 非均勻加肋耐壓殼優化結果分析

借助iSIGHT軟件分別將經1 200次試驗設計得到的二階RSM近似模型和RBF模型，結合多島遺傳算法[9，11]（multi-island genetic algorithm）按照圖2的優化流程搭建構成非均勻環肋耐壓殼優化策略。其中多島遺傳算法的參數設置如下:子群規模為15，子群個數15，總進化代數200，交叉概率pc為0.85，變異概率pm為0.01，島間遷移率為0.01，遷移的間隔代數為5。通過分析目標函數和約束條件是否滿足要求，不斷地更新優化變量，從而形成新的設計點，通過近似模型進行計算，不斷循環往復直至獲得全局最優解。通過尋優迭代最終得到各個模型的最優方案，如表4和表5所示。

表4 優化后的耐壓殼尺寸Tab.4 The particular of cylindrical pressure shell after optimization

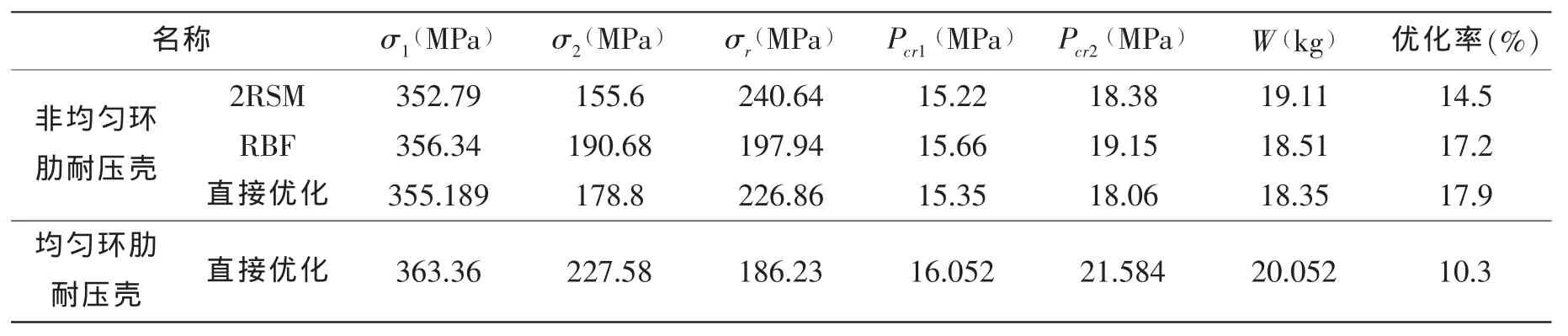
表5 耐壓殼優化結果Tab.5 The result of optimization

分析表4，表5的優化結果。對比各優化方案優化后的耐壓殼屈服強度，穩定性和重量可知，無論是使用2階RSM模型和RBF模型進行優化，其優化結果均與直接優化的結果相近。在優化過程中，使用近似模型優化方法只須在試驗設計時調用1 200次ANSYS仿真計算，而若采用直接優化的方法則須調用45 000次ANSYS仿真計算，這大大減少了仿真計算的次數。可見，使用近似模型的優化方法能以少量的仿真計算，優化出令設計者滿意的結果；由于RBF更能合理地擬合設計空間的樣本點，更真實地反應優化目標的特性，故使用RBF近似模型的優化結果比使用二階RSM近似模型的結果更為接近直接優化的優化結果。

圖3為各優化方案優化后耐壓殼一階失穩模態圖。對于均勻環肋耐壓殼艙段失穩時，為一個半波，艙段中部的位移最大。而非均勻環肋耐壓殼，通過合理對肋骨位置、剛度進行布置，使艙段中部的結構剛度加強，限定了失穩時中部的位移，從而提高艙段整體的穩定性。從失穩模態來看，經優化后非均勻環肋耐壓殼的肋骨間殼板屈曲壓力Pcr1均大于15 MPa，艙段整體總體屈曲壓力Pcr2也均大于18 MPa。故所有的優化結果均滿足1 000 m潛深對耐壓殼的結構強度要求。結合表5可知，非均勻環肋圓柱耐壓殼的優化結果與普通均勻環肋圓柱耐壓殼的優化結果相比較，無論采用何種優化方式，非均勻環肋圓柱耐壓殼優化后的重量均比普通耐壓殼輕。這表明，非均勻環肋耐壓殼是能在保證耐壓殼體的屈服和屈曲強度的前提下，通過合理的布置肋骨截面尺寸和肋骨間距，能有效地提高殼體的結構性能，能最大限度地提高材料利用率，從而降低殼體的重量。

圖3 環肋圓柱耐壓殼優化后一階失穩模態Fig.3 The deformation atlas of first order instability after optimization model

6 結 語

為提高潛水器圓柱耐壓殼的穩定性，并提高材料的利用率，本文在潛水器的圓柱耐壓殼設計中引入非均勻肋骨布置方案，并研究了近似模型技術在其優化設計過程中的應用。本文借助ISIGHT軟件采用拉丁超立方方法進行試驗設計構建出2階RSM模型和RBF模型，搭建了近似模型直接優化策略的優化方式，并利用多島遺傳算法法進行優化實現了對非均勻環肋圓柱耐壓殼的優化，得到了令人滿意的優化設計結果。經研究得出如下結論：

（1）基于近似模型的優化分析方法，在優化中，運用最優拉丁超立方的試驗設計方法，能在設計空間內，以少量仿真計算結果就能擬合出反映整個設計空間屬性的近似分析模型。代替實際仿真計算對優化問題進行分析，很大程度的減少目標函數和約束函數評估的計算量，從而加快了設計進程與效率。

（2）二次多項式RSM和RBF兩種近似模型構建的非均勻環肋圓柱耐壓殼屈服和屈曲誤差表明，RBF模型的擬合誤差明顯小于多項式響應面模型的誤差。并且能在較少的數據中擬合出輸入變量與輸出量之間的復雜關系，故在優化中采用RBF近似模型得到的優化結果更為真實可靠。

（3）相比于普通圓柱耐壓殼，非均勻加肋圓柱耐壓殼，通過合理的布置肋骨截面尺寸和肋骨間距，更大限度地發揮肋骨的作用，能有效地提高耐壓殼的屈服屈曲結構性能。故在耐壓殼的設計中，采用非均勻的加肋形式，可最大限度地提高材料利用率，從而降低潛水器的重量。

[1]呂春雷,王曉天等.多種型式加強的耐壓圓柱殼體的結構穩定性研究[J].船舶力學,2006,10(5):113-115.Lü Chunlei,Wang Xiaotian,et al.Study of bukling of cylindrical shell ring stiffened by manifold stiffeners under hydrostatic pressure[J].Journal of Ship Mechanics,2006,10(5):113-118.

[2]朱邦俊,萬正權等.半圓環殼肋骨加強的耐壓圓柱殼結構穩定性研究[J].船舶力學,2005,9(1):79-83.Zhu Bangjun,Wan Zhengquan,et al.On the buckling of cylindrical shell ring-stiffened by half-tubes under hydrostatic pressure[J].Journal of Ship Mechanics,2005,9(1):79-83.

[3]程妍雪.基于非均勻加肋理論的耐壓殼優化設計[D].哈爾濱:哈爾濱工程大學,2012:6-10.

[4]程妍雪.非均勻環肋圓柱殼穩定性研究[C].第十五屆中國海洋（岸）工程學術討論會論文集,2011:506-509.

[5]Kukbin Kim,Ulnyeon Kim,Jinsoo Park.A study on effects of initial deflection on ultimate strength of ring-stiffened cylindrical structure under external hydrostatic pressure[C]//The Thirteenth(2003)International Offshore and Polar Engineering Conference,May 25-30,2003.Honolulu,Hawaii,USA,2003:506-509.

[6]楊卓懿,龐永杰.響應面模型在耐壓殼優化設計中的應用研究[J].哈爾濱工程大學學報,2010,36(6):689-692.

[7]Jin R,Chen W,Simpson T W.Comparative studies of metamodeling techniques under multiple criterta[J].Journal of Structures and Multidisciplinary Optimization,2001,23(1):1-13.

[8]中國船級社.潛水系統與潛水器入級與建造規范[S].北京:人民交通出版社,1996:32-42.

[9]賴宇陽.Isight參數化理論與實力詳解[M].北京:航空航天出版社,2012:153-183.

[10]Shang gaofeng,Zhang aifeng,Wang zhengquan.Optimum design of cylindrical shells under external hydrostatic pressure[J].Journal of Ship Mechanics,2010,14(12):1384-1393.

[11]茍 鵬,崔維成.基于Kriging模型的深潛器多球交接耐壓殼結構優化[J].船舶力學,2009,13(1):100-106.Gou Peng,Cui Weicheng.Structural optimization of multiple inter-secting spherical pressure hulls based on kringing model[J].Journal of Ship Mechanics,2009,13(1):100-106.