垂向混合參數(shù)化方案對模擬黃海夏季上層溫度結(jié)構(gòu)的影響研究

張學峰，韓桂軍，王東曉，李威，劉克修，馬繼瑞

（1.國家海洋信息中心，天津 300171；2.中國科學院南海海洋研究所，廣東 廣州 510301）

垂向混合參數(shù)化方案對模擬黃海夏季上層溫度結(jié)構(gòu)的影響研究

張學峰1，2，韓桂軍1，王東曉2，李威1，劉克修1，馬繼瑞1

（1.國家海洋信息中心，天津 300171；2.中國科學院南海海洋研究所，廣東 廣州 510301）

采用POMgcs（Princeton Ocean Model with generalized coordinate system）和MITgcm（MIT General Circulation Model）兩個海洋數(shù)值模式，研究了M-Y2.0、基于固壁近似假定的M-Y2.5、基于波浪破碎作用的M-Y2.5和KPP 4種垂向混合參數(shù)化方案對模擬黃海夏季上層溫度結(jié)構(gòu)的影響。結(jié)果表明，M-Y2.0和基于固壁近似假定的M-Y2.5方案低估了黃海上層的湍動能，模擬的黃海夏季溫度上混合層的效果與實測相比均偏淺，不能夠很好地重構(gòu)黃海夏季溫度的垂直結(jié)構(gòu)。而基于波浪破碎作用的M-Y2.5和KPP方案均可以增加海洋上層湍動能的輸入量，模擬的黃海夏季溫度上混合層的效果與實測較為一致。故推測黃海夏季的上層結(jié)構(gòu)是受波浪混合和流場剪切等物理機制共同調(diào)節(jié)的，若通過合理的垂向混合參數(shù)化方案將這些物理機制的作用加以體現(xiàn)，將會較真實地模擬和重構(gòu)出黃海夏季海溫上層結(jié)構(gòu)。

黃海夏季溫度結(jié)構(gòu)；數(shù)值模擬；垂向混合參數(shù)化；波浪破碎

1 引言

黃海海面夏季溫度增高，海洋垂向?qū)咏Y(jié)穩(wěn)定，由動力過程（風、浪、潮等）影響的湍流混合是控制海水垂向混合的主要因素。由于湍流混合的作用，夏季黃海上層溫度出現(xiàn)10 m左右的上混合層，而黃海近岸的底層出現(xiàn)溫度鋒面，等溫線分布呈臺狀結(jié)構(gòu)。圖1是2000年8月16-17日觀測的35.5°N剖面的位置和溫度分布，在黃海上層，存在一個約10 m的混合層，在10～35 m處存在較強的溫度梯度，形成季節(jié)性溫度躍層，35 m以深溫度較低，且分布較為均勻，形成黃海底層的冷水結(jié)構(gòu)，即黃海冷水團。對中國近海海洋環(huán)流和溫鹽結(jié)構(gòu)進行模擬可以采用多種垂向混合參數(shù)化方案，研究表明，如果不選取合理的垂向湍流混合參數(shù)化方案，則很難模擬黃海夏季海溫的上層結(jié)構(gòu)。本文基于POMgcs和MITgcm兩個海洋數(shù)值模式，研究不同的垂向混合參數(shù)化方案對模擬黃海夏季海溫上層結(jié)構(gòu)的效果。

POMgcs［1］海洋模式的垂向混合參數(shù)化方案是基于Mellor和Yamada［2］的M-Y2.5方案，該方案早期是基于固壁近似假定的混合方案，未考慮波浪的混合作用。研究表明［3］，基于該湍流混合參數(shù)化方案的海洋模式，夏季增溫期數(shù)值模擬的湍流混合項較弱，難以較真實地模擬出溫度的垂直結(jié)構(gòu)。目前能夠體現(xiàn)波浪對海洋要素垂向分布影響的途徑有多種。其中一種途徑是根據(jù)前人的研究成果［4—6］，認為海表的湍動能主要是由波浪破碎等物理過程產(chǎn)生的，通過改變湍動能的邊界條件等，引入波浪破碎等效應，調(diào)整海洋模式參數(shù)。孫群等［7—10］在理論分析的基礎(chǔ)上，研究了波浪破碎對海洋上層流場的影響；Mellor和Blumberg［11］為解決模擬海溫上層分布不理想的問題，基于M-Y參數(shù)化方案，研究了在一維數(shù)值模式中通過3個途徑引入波浪破碎參數(shù)，即將M-Y的湍動能表面邊界條件改為Craig-Banner邊界條件［12］、改變M-Y的近表層的湍流混合長度尺度［13］，以及改變風應力拖曳系數(shù)，聯(lián)合考慮海表波浪破碎效應對湍動能輸入的貢獻，從而改進了湍流混合系數(shù)的參數(shù)化方案；同時還發(fā)展了一個基于POM2k的浪流耦合模式及其軟件模塊。另外，非破碎的波浪也能夠改進海洋上層混合的模擬結(jié)果［14］。本研究對于POMgcs海洋模式采用了上述第一種途徑，即根據(jù)Mellor和Blumberg的思路，試驗了在三維情況下，基于固壁近似假定，或加入波浪破碎作用的兩種參數(shù)化方案在模擬黃海海溫，尤其是模擬夏季海溫上混合層的效果。

MITgcm［15—16］海洋模式包含多項垂向參數(shù)化方案（如KPP、M-Y2.0），是ECCO（Estimating the Current and Climate of the Ocean）研究計劃中采用的主要模式，在我國也正在推廣應用，如樊孝鵬等［17］、宣基亮等［18］利用該模式做了中國近海及西北太平洋的數(shù)值研究。本文將在上述研究海域進行三維數(shù)值模擬試驗，研究該模式的M-Y2.0和KPP垂向湍流混合方案的效果。

圖1 2000年8月16-17日35.5°N剖面位置和溫度場

2 對POMgcs海洋模式垂向混合參數(shù)化的數(shù)值試驗

本試驗基于POMgcs模式，采用上述M-Y2.5的兩種垂向混合參數(shù)化方案，數(shù)值試驗海區(qū)為（24°～41° N，116°～130°E），模式網(wǎng)格水平分辨率為（1／6）°，且均勻分布；為抑制虛假的階梯效應，垂向采用混合坐標分層方案，即水深的90%以淺采用Z坐標分層，90%以深采用Sigma坐標分層，從海面到海底分25層；海區(qū)地形采用“中國海標準經(jīng)緯度水深和基準面數(shù)據(jù)表”［19］中的水深數(shù)據(jù)插值得到；強迫風場采用Quikscat日平均結(jié)果，空間分辨率分別為0.25°×0.25°。為了更好地體現(xiàn)黃海夏季海溫的垂直結(jié)構(gòu)，如潮汐鋒和溫度的臺狀結(jié)構(gòu)等，在模式的開邊界條件上加入潮位分量。本文的潮分量僅僅考慮M2、S2、K1、O14個主要分潮。

基于上述試驗配置，開展兩組三維數(shù)值試驗：基于固壁近似假定的M-Y2.5參數(shù)化方案和基于波浪破碎作用的M-Y2.5參數(shù)化方案，兩組試驗均從1986年1月開始積分，到2005年12月結(jié)束，共積分20 a。

2.1 基于固壁近似假定的M-Y2.5參數(shù)化方案數(shù)值模擬試驗分析

基于固壁近似的湍動能方程的邊界條件如下：

式中，Kq是湍流混合系數(shù)，q2為湍動能的2倍，此外，固壁近似假定認為湍流混合長度l在海表為零。

首先對模擬的溫度場和流場進行檢驗。圖2a、b分別是對黃海冬季（2月）和夏季（8月）50 m層的溫度和流場的模擬結(jié)果。冬季存在一個明顯的暖水舌從濟州島西部沿西北指向黃海中部（34°N），然后再轉(zhuǎn)向北一直延伸到渤海海峽。海溫從北向南、從近岸到離岸逐漸升高。最高溫度的海域出現(xiàn)在東海的黑潮區(qū)，由于黑潮強流的影響，等溫線分布較密。夏季，黃海冷水團是黃海夏季底層主要的特征之一，黃海冷水團被潮致溫度鋒所環(huán)繞，淺水處溫度更高，隨著水深的增加，溫度逐漸變低，這導致一個密度驅(qū)動的氣旋式環(huán)流的產(chǎn)生。以上結(jié)果均與多年實測溫度和環(huán)流結(jié)構(gòu)基本一致［20］。

圖2 黃海冬季（a）和夏季（b）50 m層的溫度和流場的模擬結(jié)果

利用該方案模擬2000年8月17日35.5°N剖面的溫度分布（圖3），上混合層深度模擬得很淺，導致溫躍層強度與實際觀測相比也較弱。對比模擬的該斷面上混合層深度和觀測深度（圖4），模擬的上混合層深度（藍線）與實測結(jié)果（黑線）相差很大。

圖3 基于固壁近似假定模擬的2000年8月17日35.5°N剖面的溫度分布

圖4 實測和模擬上混合層深度

2.2 基于波浪破碎作用的M-Y2.5參數(shù)化方案數(shù)值模擬試驗分析

采用考慮波浪破碎影響的湍動能邊界條件如下：

式中，Kq是湍流混合系數(shù)，αCB是波能因子，具有O（102）的量級。另外，考慮波浪破碎效應后，在海表附近的湍流混合長度l做了如下調(diào)整：

式中，lm是由M-Y2.5方案計算出的湍流混合長度的值，κ是馮卡門常數(shù)，取值0.41，β是海表粗糙度參數(shù)，具有O（105）的量級，g是重力加速度。Terrey等［13］通過觀測研究表明，考慮波浪破碎影響后，海洋的耗散結(jié)構(gòu)在垂向可以分為3層：最上層為波致增強層，波浪破碎所釋放的約50%能量將在該層被耗散掉；在浪致增強層的下面是過渡層，余下的約50%能量將在該層進一步被耗散；最下面一層是以剪切為主的固壁近似層，此層，湍動能的生成機制是以流場的垂向剪切為主，而由波浪破碎所釋放的能量很難傳到固壁近似層里。故l的調(diào)整深度被限制在過渡層所處的深度上。根據(jù)Craig和Banner［12］的研究結(jié)果，過渡層的深度強依賴于zw，而弱依賴于α。當α取100時，過渡層所處的深度為海表粗糙度zw的6倍，故在本文中，l的調(diào)整深度為6zw。值得指出的是，在波致增強層中，lm一般要小于κzw，即由波浪破碎生成的湍動能在該層占主導地位，而在過渡層中，波浪破碎的作用不一定比剪切的作用大，即κzw不一定大于lm，二者的大小取決于當?shù)仫L場和流場等多種因素，在固壁近似層中，則完全以流場的剪切為主。

圖5 基于波浪破碎作用模擬的2000年8月17日35.5°N剖面的溫度分布

當引入波浪破碎邊界條件后，則能夠模擬出較為理想的上混合層效果（圖5）。這表明引入波浪破碎機制后，能夠增加表層的湍動能輸入量，進而加大了夏季黃海上層的湍流混合強度，可以對黃海夏季海溫的垂直結(jié)構(gòu)進行較理想的模擬和再現(xiàn)。從圖4可見，經(jīng)該方案模擬的上混合層深度（紅線）較上述基于固壁近似假定的M-Y2.5參數(shù)化方案的模擬結(jié)果（藍線）有較大的改善。

圖6是搜集得到的1986-2005年黃海夏季（6 -8月之間）的部分觀測剖面分布情況，這些剖面來自WOD09、GTSPP以及國內(nèi)公開調(diào)查資料，共2 000多個觀測剖面。對比觀測和兩組試驗模擬結(jié)果，基于波浪破碎作用的結(jié)果比基于固壁近似假定的結(jié)果有明顯的提高（表1）。基于波浪破碎作用的結(jié)果模擬的上混合層深度比基于固壁近似假定的結(jié)果大約提高了3 m以上。此外，模擬的20 m以淺平均溫度相比基于固壁近似假定的結(jié)果也有了明顯的改進。

表1 觀測和POMgcs模擬結(jié)果

圖5和表1的結(jié)果表明，經(jīng)該方案模擬的上混合層深度與觀測結(jié)果相比仍有一定差距，原因之一是對波浪破碎參數(shù)的選取還存在一定的經(jīng)驗性，之二是M-Y2.5方案對風的攪拌作用估計不足。

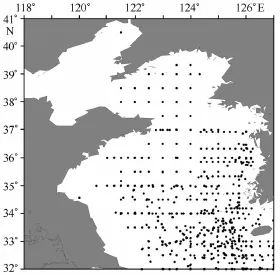
圖6 搜集得到1986-2005年黃海夏季（6-8月）部分觀測剖面分布

為更深入的研究波浪破碎對黃海夏季上層混合的影響，對湍動能方程中的各項進行了診斷計算。為此，將湍動能方程寫成笛卡爾坐標形式如下：

式中，q2代表湍動能，Pd、Ps、Pb和ε分別為垂向擴散項、剪切生成項、浮力生成項和耗散項，F(xiàn)q是水平擴散項，ρ0是海水的參考密度，g是重力加速度，u、v是流場的東分量與北分量，?ρ?是海水的密度梯度減?z去絕熱損失率。Kq、KM和KH分別是湍流、流速和溫鹽的垂向混合系數(shù)，按如下公式計算：

式中，Sq、SM和SH是依賴于理查森數(shù)的穩(wěn)定函數(shù)。

利用上述兩種參數(shù)化方案對（35°N，123°E）處夏季診斷計算結(jié)果如圖7和圖8所示。當未考慮波浪破碎影響時，黃海上層主要體現(xiàn)了剪切生成項與耗散項之間的平衡，而其它幾項相對于二者來說是小量（圖7a，水平擴散項量級較小，沒有繪出），這說明湍流主要是由流場的垂向剪切生成，這與海洋上層湍流耗散率的實際觀測不符，由此得到的垂向混合系數(shù)量級較小（圖7b），這表明僅僅依靠流場的垂向剪切并不能提供足夠的能量使海水混合均勻，故而模擬的黃海上混合層（等溫層）與實際的溫度觀測剖面相比較淺，深度不足5 m。當考慮波浪破碎的影響時，這時黃海上層主要是垂向擴散項與耗散項的平衡，而剪切生成項相比二者為小量（見圖8a），這表明由于波浪的破碎，促使黃海上層湍流的耗散率提高了兩個量級以上，進而增強了黃海上層的混合（見圖8b），使黃海上層混合更加均勻，較大程度上加深了海洋上混合層的深度（接近10 m）。以上結(jié)果表明，黃海由波浪破碎導致的湍耗散比剪切流導致的湍流耗散要大兩個量級以上，若不考慮波浪破碎的影響，黃海上層缺乏足夠的能量促使海水混合均勻。

圖7 基于固壁近似的M-Y2.5的診斷計算結(jié)果（a）和垂向混合系數(shù)KH（b）

3 對MITgcm海洋模式垂向混合參數(shù)化的數(shù)值試驗

MITgcm是20世紀90年代由美國麻省理工學院（MIT）發(fā)展起來的海洋數(shù)值模式，在該數(shù)值模式中，采用切削網(wǎng)格方式來抑制虛假的階梯效應。本數(shù)值試驗方案除了垂向采用Z坐標并按標準層分層以外，其他試驗配置條件均與POMgcs配置一致。

3.1 基于M-Y2.0垂向混合方案的數(shù)值模擬試驗分析

利用MITgcm模式，基于M-Y2.0垂向混合方案模擬2000年8月17日35.5°N剖面溫度場（見圖9）。經(jīng)該方案模擬的上混合層深度較淺，底層溫度模擬的不夠理想。由于該方案既未考慮波浪破碎的作用，又低估了風場的攪拌和流場垂向剪切的作用，故模擬的該斷面上混合層深度很淺（見圖10藍線），不能真實地反映出黃海夏季海溫上混合層的結(jié)構(gòu)特征。統(tǒng)計表明，模擬的上混合層深度為2.46 m，與觀測的上混合層深度（9.66 m）相差很大，而20 m以淺平均溫度為18.22℃，比實測低了超過1℃（見表2），模擬結(jié)果不理想。

圖8 基于波浪破碎作用的M-Y2.5的診斷計算結(jié)果（a）和垂向混合系數(shù)KH（b）

圖9 基于M-Y2.0模擬的2000年8月17日35.5°N剖面的溫度分布

圖10 實測和模擬上混合層深度

3.2 基于KPP垂向混合方案的數(shù)值模擬試驗分析

MITgcm的另一種湍流閉合方案是KPP［21］，KPP方法由Large等發(fā)展，后經(jīng)Durski等［22］改進，在考慮風攪拌的表面邊界層的基礎(chǔ)上，在內(nèi)區(qū)考慮了由速度剪切和內(nèi)波引起的混合效應。采用MITgcm模式KPP方案模擬35°N斷面2月、5月、8月和11月平均溫度、鹽度的垂直結(jié)構(gòu)（見圖11）。2月，溫度和鹽度均垂向混合均勻（見圖11a、b）；5月，溫度躍層和上混合層不明顯，鹽度混合仍較均勻（見圖11c、d）；8月，溫度已形成較強的躍層，上混合層厚度可達10 m左右，底部保留了冬季冷水的特性，形成黃海冷水團，并且雙冷核結(jié)構(gòu)比較明顯，但鹽度始終沒有形成躍層結(jié)構(gòu)（見圖11e、f）；11月，由于海溫下降，上混合層和溫躍層較夏季均明顯加深（見圖11g、h）。以上模擬結(jié)果均與多年實測溫度結(jié)構(gòu)相符合［20］。利用上述方案對黃海冬季的黃海暖流以及夏季的黃海冷水團及其相關(guān)特征模擬結(jié)果均比較合理（見圖12）。基于KPP垂向混合方案模擬的2000年8月17日35.5°N剖面溫度場，上混合層、溫躍層和底層冷水均模擬得較為理想（見圖13）。經(jīng)該方案模擬的上混合層深度（紅線）與實測較為接近，能夠較好的反映黃海夏季的上混合層結(jié)構(gòu)特征（圖10）。經(jīng)該方案模擬的上混合層平均深度為9.21 m，20 m以淺平均溫度為20.31°C（見表2），上述模擬結(jié)果遠好于經(jīng)M-Y2.0方案模擬的結(jié)果，故由KPP垂向混合方案能夠較好地模擬出黃海的上混合層，也能夠較準確的反映該海域的溫度垂直結(jié)構(gòu)。

圖11 35°N斷面2、5、8、11月溫度和鹽度分布

圖12 黃海冬季（a）和夏季（b）底層的溫度和環(huán)流結(jié)構(gòu)

圖13 基于KPP模擬的2000年8月17日35.5°N剖面的溫度分布

表2 觀測和MITgcm模式模擬結(jié)果

4 小結(jié)與討論

本文采用兩種海洋數(shù)值模式，針對每種海洋數(shù)值模式的不同垂向混合參數(shù)化方案，分別對黃海溫度垂直結(jié)構(gòu)進行了數(shù)值模擬試驗，得到的結(jié)論如下：

（1）POMgcs模式基于固壁近似假定的M-Y2.5參數(shù)化方案，以及MITgcm模式基于M-Y2.0方案由于未考慮波浪對海洋上層的混合作用，故黃海上層的湍動能均較弱，海溫上混合層的模擬效果較差，難以很好的重構(gòu)出黃海夏季的溫度結(jié)構(gòu)特征。

（2）POMgcs模式基于波浪破碎作用的MY2.5參數(shù)化方案，考慮了上層波浪破碎增加的湍動能輸入，可以較準確的反映該海域的溫度垂直結(jié)構(gòu)。需要說明的是，在POMgcs模式基于波浪破碎作用的參數(shù)化方案試驗中，上述波能因子αCB和海表粗糙度參數(shù)β的量值還存在一定的經(jīng)驗性，實際上類似這些參數(shù)還可以通過數(shù)據(jù)同化的途徑對其進行最優(yōu)估計［23］。

（3）基于波浪破碎作用的M-Y2.5參數(shù)化方案，是在湍動能方程中引入一個湍動能的輸入源，一些學者推斷這部分湍動能主要是由波浪破碎產(chǎn)生的，但這依然是一個值得討論的學術(shù)問題。

（4）MITgcm模式基于KPP的垂向混合方案，對黃海夏季的上混合層模擬也有較好的效果，Baylor等［24］指出，波浪的一部分非破碎效應（Langmuir環(huán)流的混合作用）實際上已經(jīng)隱式的體現(xiàn)在KPP方案中，說明了波浪的非破碎效應對于黃海夏季的上層混合來說是非常重要的。波浪的非破碎混合作用也可以被顯示的加到KPP方案中以改進海洋上層的混合效果［25］。

（5）黃海夏季的上層結(jié)構(gòu)是受波浪混合和流場剪切等物理機制共同調(diào)制的［26—27］，除波浪破碎的作用外，波浪的非破碎作用也會加強陸架海上層的垂向混合［28］，若通過合理的垂向混合參數(shù)化方案將這些物理機制的作用加以體現(xiàn)，將會較真實地模擬和重構(gòu)出黃海夏季海溫上層結(jié)構(gòu)。

致謝：感謝黃瑞新和Peter C Chu對本文提出的寶貴建議！

參考文獻：

［1］Mellor G L，Sirpa H，Tal E，et al.A generalization of a sigma coordinate model and an intercomparison of model vertical grids［M］／／Ocean Forecasting：Conceptual Basis and Application.German：Springer-Verlag，2002：55-72.

［2］Mellor G L，Yamada T.Development of a turbulence closure models for geophysical fluid problems［J］.Rev Geophys，1982，20：851-875.

［3］Martin P J.Simulation of the mixed layer at OWS November and Papa with several models［J］.J Geophys Res，1985，90：581-597.

［4］Kitaigorodskii S A，Lumley J L.Wave-turbulence interactions in the upper ocean.Part I：The energy balance of the interacting fields of surface wind waves and wind-induced three-dimensional turbulence［J］.J Phys Oceanogr，1983，13：1977-1987.

［5］Thorpe S A.Energy loss by breaking waves［J］.J Phys Oceanogr，1993，23：2498-2502.

［6］Drennan W M，Donelan M A，Terray E A，et al.Ocean turbulence dissipation measurements in SWADE［J］.JPhys Oceanogr，1996，26：808-815.

［7］孫群.海浪破碎對海洋上混合層影響的數(shù)值研究［D］.青島：中國海洋大學，2003.

［8］孫群，管長龍，宋金寶.海浪破碎對海洋上混合層中湍能量收支的影響［J］.海洋與湖沼，2006，37（1）：69-74.

［9］Sun Qun，Guan Changlong，Song Jinbao.Wave breaking on turbulent energy budget in the ocean surface mixed layer［J］.Chinese Journal of Oceanology and Limnology，2007，26（1）：9-13.

［10］Sun Qun，Song Jinbao，Guan Changlong.Simulation of the ocean surface mixed layer under the wave breaking［J］.Acta Oceanologica Sinica，2005，24（3）：9-15.

［11］Mellor G L，Blumberg A F.Wave breaking and ocean surface layer thermal response［J］.J Phys Oceanogr，2004，34：693-698.

［12］Craig P D，Banner M L.Modeling wave-enhanced turbulence in the ocean surface layer［J］.J Phys Oceanogr，1994，24：2546-2559.

［13］Terray E A，Drennan W M，Donelan M A.The vertical structure of shear and dissipation in the ocean surface layer［C］／／Proc.Symp.on the Wind-driven Air-Sea Interface-Electromagnetic and Acoustic Sensing，Wave Dynamics and Turbulent Fluxes.Sydney：University of New South Wales，2000：239-245.

［14］喬方利，馬建，夏長水，等.波浪和潮流混合對黃海、東海夏季溫度垂直結(jié)構(gòu)的影響研究［J］.自然科學進展，2004，14（12）：1434-1441.

［15］Marshall J，Hill C，Perelman L，et al.Hydrostatic，quasi-hydrostatic and nonhydrostatic ocean modelling［J］.J Geophysical Res，1997，102（C3）：5733.

［16］Marshall J，Hill C，Perelman L，et al.A finite-volume，incompressible Navier Stokes model for studies of the ocean on parallel computers［J］.J Geophysical Res，1997，102（C3）：5753.

［17］樊孝鵬，黃大吉，章本照.東海黑潮的氣候態(tài)數(shù)值模擬［J］.浙江大學學報（工學版），2006，40（5）：916-920.

［18］宣基亮，黃大吉，章本照.宮古海峽通道海流的高分辨率數(shù)值模擬［J］.海洋學研究，2008，26（1）：1-10.

［19］林美華，方國洪.中國海標準經(jīng)緯度水深和基準面數(shù)據(jù)表［M］.青島：中國科學院海洋研究所，1999.

［20］蘇紀蘭，袁業(yè)立.中國近海水文［M］.北京：海洋出版社，2005.

［21］Large W G，McWilliams J C，Doney S C.Oceanic vertical mixing：A review and a model with a nonlocal boundary layer parameterization［J］.Rev Geophys，1994，32：363-403.

［22］Dursku S M，Glenn S M，Haidvogel D B.Vertical mixing schemes in the coastal ocean：Comparison of the level 2.5 Mellor-Yamada scheme with an enhanced version of the K profile parameterization［J］.J Geophysical Res，2004，109（C01015）：1029-1051.

［23］張學峰，韓桂軍，王東曉，等.同化海溫觀測數(shù)據(jù)研究波浪破碎對海洋上層結(jié)構(gòu)的影響［J］.熱帶海洋學報，2011，30（5）：48-54.

［24］Baylor F K，Adrean W.Langmuir parameterizations［R］／／13th CCSM Meeting-OMWG session，2008.

［25］Shu Qi，Qiao Fangli，Song Zhenya，et al.Improvement of MOM4 by including surface wave-induced vertical mixing［J］.Ocean Modelling，2011，40（1）：42-51.

［26］Zhang Xuefeng，Han Guijun，Wang Dongxiao，et al.Effect of surface wave breaking on the surface boundary layer of temperature in the Yellow Sea in summer［J］.Ocean Modelling，2011，38（3／4）：267-279.

［27］Zhang Xuefeng，Han Guijun，Wang Dongxiao，et al.Summer surface layer thermal response to surface gravity waves in the Yellow Sea［J］.Ocean Dynamics，2012，62：983-1000.

［28］Zhang Xuefeng，Han Guijun，Wang Xidong，et al.Effects of Stokes production on summer ocean shelf dynamics［J］.Acta Oceanologica Sinica，2014，33（1）：24-34.

The effect of the vertical mixing parameterization on modeling the summer structure of temperature in the Yellow Sea

Zhang Xuefeng1，2，Han Guijun1，Wang Dongxiao2，Li Wei1，Liu Kexiu1，Ma Jirui1

（1．National Marine Data and Information Service，Tianjin 300171，China；2．South China Sea Institute of Oceanology，Chinese A-cademy of Science，Guangzhou 510301，China）

Four vertical mixing parameterization schemes，including M-Y2.0，M-Y2.5 based on wall layer proximity，M-Y2.5 based on surface wave breaking and KPP are applied to simulate the upper structure of temperature in the Yellow Sea in summer，using Princeton Ocean Model with generalized coordinate system（POMgcs）and MIT General Circulation Model（MITgcm）.It shows that the depth of the upper mixed layer simulated by M-Y2.0 and MY2.5 based on wall layer proximity are both too shallow comparing with the observation.The two schemes mentioned above can hardly well simulate the summer structure of temperature in the Yellow Sea，while both the schemes of the M-Y2.5 based on surface wave breaking and KPP have favorable capability to reconstruct the summer upper mixing layer of temperature in the Yellow Sea.So we suggest that surface wave-induced mixing and flow shear modulate jointly the upper layer structure in the Yellow sea.The upper layer structure of temperature is able to be well simulated through utilizing the rational schemes of vertical mixing parameterization that can embody the effect of the physics processes mentioned above.

parameterization；the Yellow Sea；POM；KPP；wave breaking

P731.2

A

0253-4193（2014）03-0073-10

2012-01-21；

2013-12-22。

國家973計劃課題（2013CB430304）；國家自然科學基金項目（41030854，41106005，41176003，41206178）；國家863計劃課題（2013AA09A505）；國家科技支撐計劃資助（2011BAC03B02-01-04）。

張學峰（1978-），男，遼寧省本溪市人，主要從事海洋數(shù)據(jù)同化和海洋數(shù)值模擬方面研究。E-mail：zhangxf＠m(xù)ail.nmdis.gov.cn

張學峰，韓桂軍，王東曉，等.垂向混合參數(shù)化方案對模擬黃海夏季上層溫度結(jié)構(gòu)的影響研究［J］.海洋學報，2014，36（3）：73-82，

10.3969／j.issn.0253-4193.2014.03.008

Zhang Xuefeng，Han Guijun，Wang Dongxiao，et al.The effect of the vertical mixing parameterization on modeling the summer structure of temperature in the Yellow Sea［J］.Acta Oceanologica Sinica（in Chinese），2014，36（3）：73-82，doi：10.3969／j.issn.0253-4193.2014.03.008