基于改進粒子群優化的探地雷達波形反演算法

鄭 適 張安學 岳思橙 蔣延生

?

基于改進粒子群優化的探地雷達波形反演算法

鄭 適 張安學*岳思橙 蔣延生

(西安交通大學電信學院 西安 710049)

探地雷達工作的最終目的是反演解釋地下結構參數，由于大多數反演問題是非線性的，研究非線性的反演方法具有重要意義。該文提出基于改進粒子群優化方法的探地雷達反演問題，該算法以信號均方誤差為目標函數，用時域有限差分方法作為正演工具。通過與基于遺傳算法等反演方法的結果對比，說明了該算法兼顧了準確性和簡便性；通過對模型復雜、參數多、信噪比差的仿真數據的反演結果，說明了該算法對多參數反演的有效性和良好的抗噪性；對實測數據的反演結果，進一步驗證了該算法的可行性。

探地雷達；反演算法；非線性；粒子群優化

1 引言

粒子群反演算法在模型空間中隨機地進行全局搜索，不容易陷入局部最小，同時，該方法具有實施簡便、易于施加先驗約束條件、適于并行計算等優點[13,14]。本文提出了基于改進PSO的探地雷達反演算法，應用時域有限差分方法[15]作為正演手段，以信號均方誤差作為目標函數，將改進的PSO方法應用于探地雷達的反演問題中。對仿真數據和實測數據的反演結果，說明了該方法的可行性和有效性。本文首先介紹PSO的基本原理，闡述應用改進PSO的探地雷達反演算法，然后分析仿真數據的反演結果，最后在此基礎上處理探地雷達實測數據并分析反演結果。

2 算法描述

2.1 基于粒子群優化的探地雷達反演算法

在探地雷達中，接收波形既包含信號的幅度信息，又包含相位與反射波的時延等信息。為了有效利用反射信號的所有信息，以波形的差異作為反演的目標函數，即實際接收信號與模型正演信號的均方誤差：

粒子群優化的思想基于生物學中關于群體智能的研究成果。對鳥群飛行的研究發現，一只鳥僅追蹤它有限數量的鄰居，但最終的整體結果似乎在一個中心的控制之下，即復雜的全局行為是由簡單規則的相互作用引起的。PSO即源于對鳥群捕食行為的研究。假設某區域內的一群鳥正在隨機搜索食物，此區域內只有一塊食物，每只鳥均不知曉食物的具體位置，但卻知曉各自距食物的距離，同時它們之間可以互相通信，那么合理的搜索策略即是每只鳥都向距離食物最近的那只鳥移動。PSO算法即從這種模型中得到啟示而產生。在PSO算法模型中，優化問題的每一個潛在解對應搜索空間中的一只鳥，稱之為“粒子”。每個粒子都有一個適應值和速度，適應值由目標函數決定，速度決定它飛行的方向和距離。各個粒子記憶、追隨當前的最優粒子。算法將優化問題的解初始化為一群隨機粒子，在每次迭代中，粒子通過跟蹤兩個極值——個體極值點和全局極值點來更新自己。個體極值點是粒子本身在其有限的鄰居中找到的最優解，這些鄰居是整個種群的一部分而不是全部；全局極值點是整個種群中所有粒子的最優解。

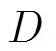
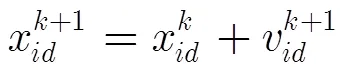
2.2 基于改進粒子群優化的探地雷達反演算法

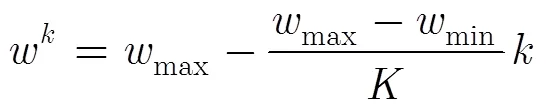
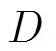
3 仿真數據及野外實測數據反演結果

3.1 仿真數據反演結果

3.1.1與基于原始粒子群的反演方法和基于遺傳算法的反演方法的結果對比 構造一個包含2層結構的地層模型，分層的幾何構造及每層的相對介電常數如圖2(a)所示。上下兩層媒質的相對介電常數分別為5, 12。兩層媒質的分界面具有一定傾斜程度，斜率=0.05，分界面起點深度=0.8 m，設定橫向探測距離為1.5 m，縱向最大探測深度為2.0 m。設天線距離地面的距離為0.5 m，接收天線與發射天線之間距離為0.2 m，由FDTD正演得到的回波信號如圖2(b)所示。

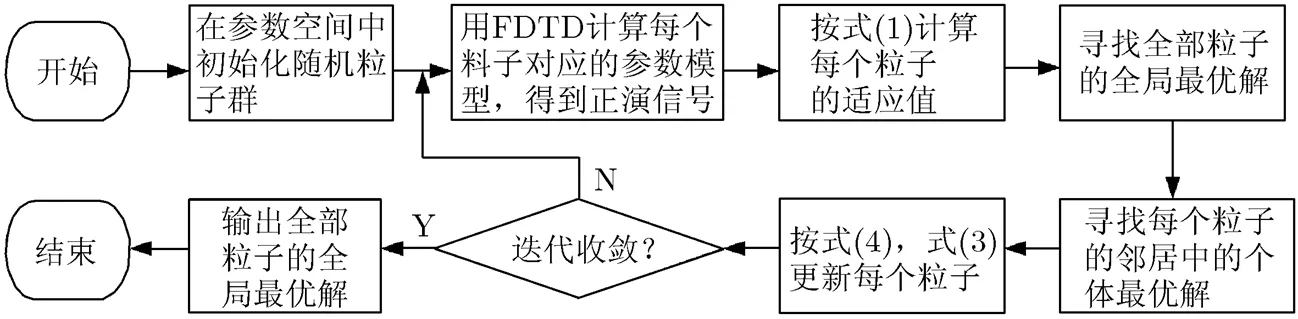
圖1 基于改進PSO的探地雷達反演算法流程圖

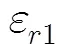
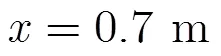
表1反演算法結果

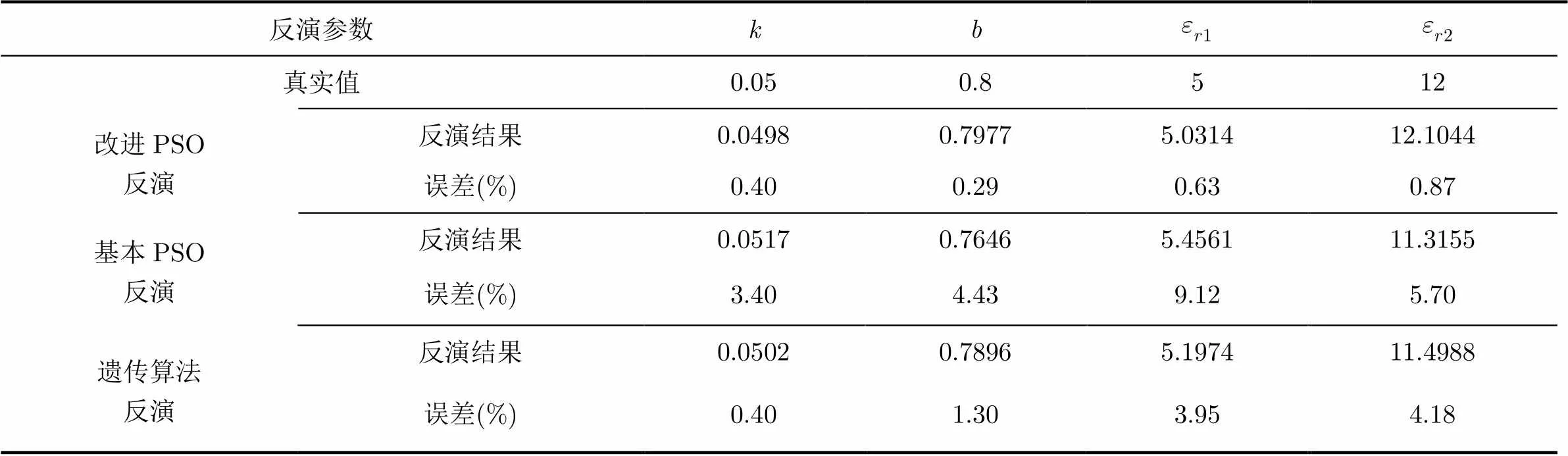
反演參數kb 真實值0.050.8512 改進PSO反演反演結果0.04980.79775.031412.1044 誤差(%)0.400.290.630.87 基本PSO反演反演結果0.05170.76465.456111.3155 誤差(%)3.404.439.125.70 遺傳算法反演反演結果0.05020.78965.197411.4988 誤差(%)0.401.303.954.18

圖3 3種反演方法的結果對比

3.1.2復雜模型的反演 建立復雜的地下模型如圖4(a)所示。

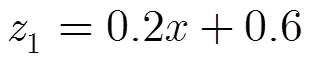
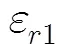
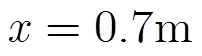
3.2 野外實測數據的反演

3.2.1實例1 為了驗證本文算法對實測數據的有效性，本文作者進行了實地測量，針對野外采集到的雷達接收數據，用本文算法進行反演。采集地點為西安交通大學西一樓側面路面施工處。探地雷達型號為美國地球物理測量系統公司的TerraSIRchSIR -3000型探地雷達，天線頻率為900 MHz，時窗長度為25 ns，測量模式為距離(測量輪控制測量)模式。路基分層照片如圖6(a)所示，該路基上面兩層分別為水泥層和混雜有雜物的黏土層，水泥層厚度約為16 cm，黏土層厚度約為50 cm。黏土層以下還有其他分層，但由于測量時窗為50 ns，黏土層以下媒質的反射信息將不包括在接收信號中，因此反演時不考慮黏土層以下的結構。探地雷達接收數據如圖6(b)所示。

圖4 復雜的地層模型及其正演回波信號

表2復雜模型的反演結果

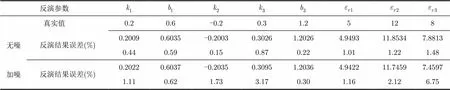
反演參數 真實值0.20.6-0.20.31.25128 無噪反演結果誤差(%)0.20090.6035-0.20030.30261.20264.949311.85347.8813 0.440.590.150.870.221.011.221.48 加噪反演結果誤差(%)0.20220.6037-0.20350.30951.20364.942211.74597.4597 1.110.621.733.170.301.162.126.75

表3實測數據的反演結果

反演參數 反演結果0.16514.500013.9277

3.2.2實例2 本文作者用同一探地雷達系統對中國某鐵路隧道襯砌進行了實際測量，測量場景如圖8(a)所示，實測數據如圖8(b)所示。應用基于改進PSO的方法對這段實測數據進行反演，結果如圖8(c)和圖8(d)所示。圖8(c)繪出了隧道襯砌厚度解釋曲線；用反演出的模型作正演，得到的反演數據如圖8(d)。將圖8(c)厚度解釋曲線的結果與鉆孔測量厚度的結果比較，兩者基本吻合，說明基于改進PSO的反演方法準確估計了襯砌厚度。從圖8(d)的反演數據和圖8(b)的實測數據比較看來，該反演算法達到了較為理想的效果。從圖8(d)的整個反演剖面來看，該反演算法能夠適應媒質電磁參數的橫向變化，能夠清楚刻畫襯砌層與底層的分界面。

4 結束語

本文將改進的粒子群優化算法應用于探地雷達反演問題中，用信號的均方誤差作為優化目標函數，以時域有限差分方法作為正演工具，提出基于改進PSO的探地雷達反演算法。首先描述該算法的原理和實現過程，然后通過對仿真數據和實測數據的處理，準確反演得到了地下模型結構，驗證了該算法的有效性和可行性。在反演結果中，將該算法與基于原始PSO的反演方法和常用的基于遺傳算法的反演方法作對比，證明了本算法具有更高的準確率，同時算法實施起來更簡便；另外，采用本算法對模型復雜、參數較多、信噪比較差情況下的仿真數據進行反演，結果說明了該算法可以有效地反演多參數模型，同時具有良好的抗噪性；最后，將本算法應用于實測數據，反演結果與實際情況吻合度較高，說明了該算法對實測數據的有效性。多種情況的實驗結果共同驗證了該算法的可行性。

圖6 實測場景及數據

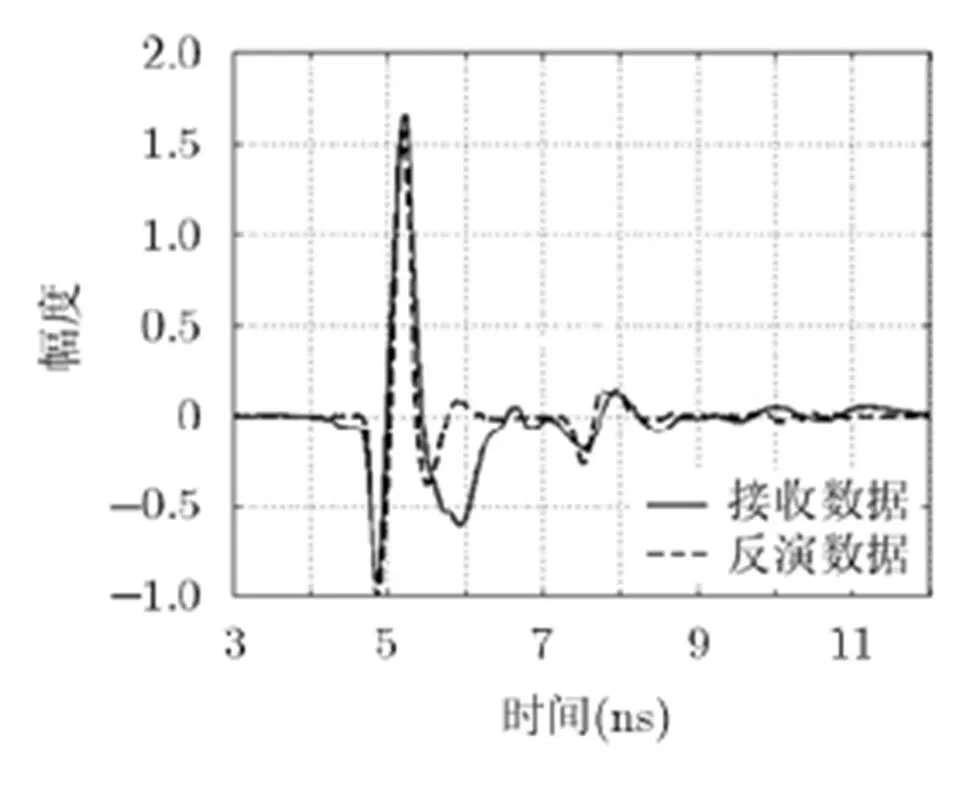
圖7 實測數據的反演結果

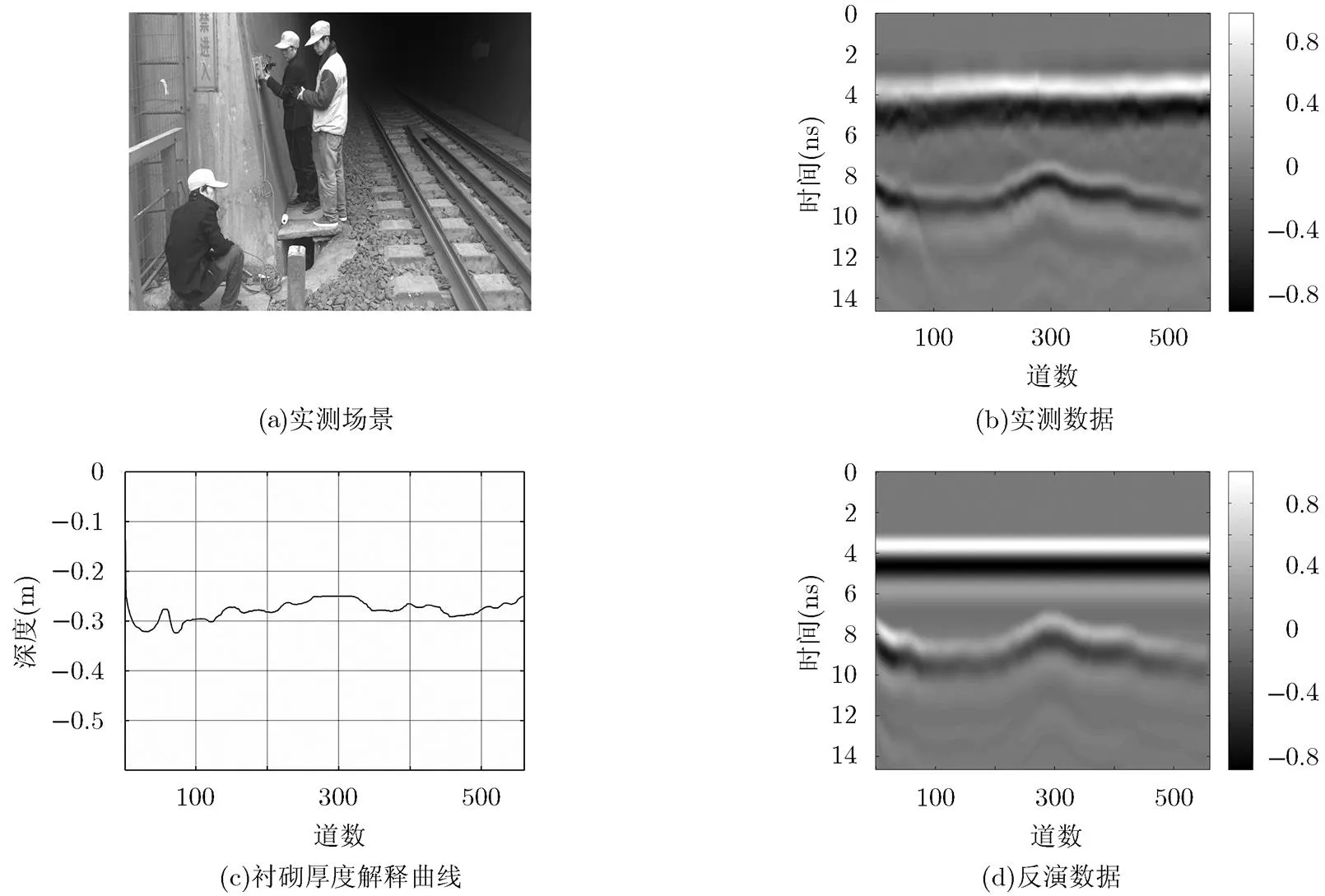
圖8 實例數據的測量與反演結果

[1] Neal A. Ground-penetrating radar and its use in sedimentology: principles, problems and progress[J].-, 2004,66(3/4): 261-330.

[2] 王家映. 地球物理反演理論[M]. 武漢: 中國地質大學出版社, 2002: 1-3.

Wang Jia-ying. Geophysical Inverse Theory[M]. Wuhan: China University of Geoscience Press, 2002: 1-3.

[3] Spagnolini U and Rampa V. Multitarget detection/tracking for monostatic ground penetrating radar: application to pavement profiling[J]., 1999,37(1): 383-394.

[4] 黃忠來, 張建中, 黃吉林. 探地雷達薄層信號的譜反演算法[J]. 大地測量與地球動力學, 2011,31(4): 154-159.

Huang Zhong-lai, Zhang Jian-zhong, and Huang Ji-lin. A sepectral inversion algorithm for GPR signals of thin layers[J]., 2011, 31(4): 154-159.

[5] 俞燕濃, 方廣有. 一種反演地下介質參數的新算法[J]. 電子與信息學報, 2009,31(03): 619-622.

Yu Yan-nong and Fang Guang-you. A new algorithm for underground medium parameters inversion[J].&, 2009, 31(03): 619-622.

[6] Khan T and Smirnova A. 1D inverse problem in diffusion based optical tomography using iteratively regularized Gauss-Newton algorithm[J]., 2005,161(1): 149-170.

[7] Gustafsson M and He S L. A wave-splitting based optimization approach to multi-dimensional time-domain electromagnetic inverse problems[J]., 1999,50(5/6): 541-551.

[8] Chang Xu-hua and Wang Yan-ming. Coal fire depth-profile reconstruction from ground penetrating radar data[J]., 2012,15(11A): 4647-4652.

[9] Aghasi A, Mendoza-Sanchez I, and Miller E L. A geometric approach to joint inversion with applications to contaminant source zone characterization[J]., 2013,29(11). DOI: 10.1088/0266-5611/29/11/115014.

[10] 易遠元, 王家映. 粒子群反演方法[J]. 工程地球物理學報, 2009,6(4): 385-389.

Yi Yuan-yuan and Wang Jia-ying. Particle swarm optimization inversion method[J]., 2009, 6(4): 385-389.

[11] Yan Z and Gu H. Non-linear prestack seismic inversion with global optimization using an edge-preserving smoothing filter[J]., 2013,61(4): 747-760.

[12] Chiu Chien-ching and Li Jhuo-ru. Image reconstruction of perfectly conducting objects by a cascaded method[J]., 2013,219(11): 6093-6105.

[13] Cui Y, Ji T, Li X,. Inversion of multi-anomalies in resistivity profiling based on particle swarm optimization[J]., 2013,28(4): 2164-2170.

[14] Toushmalani R. Gravity inversion of a fault by particle swarm optimization (PSO)[J]., 2013, 2: 315.

[15] Werner G R, Bauer C A and Cary J R. A more accurate, stable, FDTD algorithm for electromagnetics in anisotropic dielectrics[J]., 2013,255(12): 436-455.

[16] Shi Y H and Eberhart R. A modified particle swarm optimizer[C]. 1998 IEEE International Conference on Evolutionary Computation, Anchorage, 1998: 69-73.

[17] Shi Y and Eberhart R. Empirical study of particle swarm optimization[C]. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99(Cat. No. 99TH8406), Washington DC, 1999: 1945-1950.

[18] 舒志樂. 隧道襯砌內空洞探地雷達探測正反演研究[D]. [博士論文], 重慶大學, 2010.

Shu Zhi-le. Study on GPR forward simulation and inversion of tunnel lining cavity[D]. [Ph.D. dissertation], Chongqing University, 2010.

鄭 適： 女，1990年生，博士生，研究方向為探地雷達信號處理.

張安學： 男，1972年生，教授，研究方向為天線陣列信號處理、超寬帶雷達系統及其目標成像、檢測、識別算法研究，電磁場數值計算，超材料理論及其應用研究等.

Ground Penetrating Radar Inversion Algorithm Based on Improved Particle Swarm Optimization

Zheng Shi Zhang An-xue Yue Si-cheng Jiang Yan-sheng

(,’,’710049,)

Inversion and interpretation of underground structure are ultimate aim of Ground Penetrating Radar (GPR) working. Most of inversion problems are non-linear, hence, investigations of non-linear inversion methods are significant. In this paper, an improved Particle Swarm Optimization (PSO) is used to solve GPR inverse problem. Comparison results with other inversion including the genetic algorithm show that the proposed method has higher accuracy and better simplicity; inversion results under a condition of complicated model, multi- parameter and low SNR indicate the effectiveness dealing with multi-parameter and better anti-noise ability of the proposed algorithm; the inversion results of actual measurement data further verify the feasibility of this algorithm.

Ground Penetrating Radar (GPR); Inversion algorithm; Non-linear; Particle Swarm Optimization (PSO)

TN959.3

A

1009-5896(2014)11-2717-06

10.3724/SP.J.1146.2013.01979

張安學 anxuezhang@mail.xjtu.edu.cn

2013-12-19收到，2014-04-03改回

國家自然科學基金(61331005, 61001039)和中國科學院電磁輻射與探測技術重點實驗室資助課題