基于主成分分析法的火電廠選址綜合決策

唐學文

(廣西電網(wǎng)公司南寧供電局，廣西 南寧 530031)

1 引言

火電廠的選址是在滿足一定可靠性約束的條件下尋求投資與運行費用最優(yōu)的方案。這種單一追求成本最少的做法，必然是以其他目標被犧牲作為代價的。目前，許多研究都試圖在發(fā)電廠規(guī)劃［1－4］模型中盡可能去朵考慮一些相關影響因素，但是在優(yōu)化規(guī)劃階段還是不容易將這些關聯(lián)又矛盾的因素綜合到同一個模型里進行求解。發(fā)電廠規(guī)劃方案的綜合決策可以彌補規(guī)劃階段的一些不足，對規(guī)劃后確定的一些方案，從可靠性、經(jīng)濟性、適應性、環(huán)保性等多個方面進行定性或者定量的評價，最后建立數(shù)學模型對單個指標評價信息進行綜合，得到最終確定的最優(yōu)規(guī)劃方案。

現(xiàn)行的火電廠綜合評價應用中，常用的方法有模糊綜合評價法、層次分析法以及兩種方法的結合。文獻［5］綜合考慮了火電廠建設可行性的社會效益、經(jīng)濟效益、環(huán)境效益等多個因素，通過模糊綜合評判法對火電廠的選址問題進行綜合決策。文獻［6］利用熵權法來處理火電廠選址評價中客觀存在的不確定性與模糊性，熵反映數(shù)據(jù)本身的效用值求解各指標的權值，最后多層次模糊綜合評價法得到方案優(yōu)選結果。文獻［7］綜合灰決策方法與層次分析法，針對某些因素信息不完全的灰色性特點，進行火電廠規(guī)劃選址決策。解決了傳統(tǒng)建模方法和層次分析法難以解決的問題。文獻［8］利用層次分析法結合定性和定量指標，首次對多目標多層次的火電廠選址問題進行了討論。文獻［9］建立了層次分析法和模糊綜合評判法相結合的模型，解決了火電廠選址的綜合決策問題。

目前解決火電廠規(guī)劃方案綜合決策問題的兩種主流方法層次分析法和模糊綜合評判法。這兩種方法對各指標進行賦權都是由專家進行評判，比較容易受專家知識、經(jīng)驗、個人偏好的影響，主觀隨意性和不確定性較大。并且沒有充分挖掘利用客觀數(shù)據(jù)所提供的信息。

考慮上文所說的這些缺點，本文將主成分分析法(PCA)引入到火電廠選址方案的綜合決策領域。采用主成分分析法僅利用客觀數(shù)據(jù)便能得到方案的最后評價結果，評價結果相對客觀。主成分分析法的基本原理與上述兩種主流方法有較大的區(qū)別，它對解決火電廠選址優(yōu)化決策系統(tǒng)開發(fā)和完善具有一定的參考價值。

2 火電廠選址方案綜合評價指標體系

火電廠選址優(yōu)選決策受到多種因素的影響，本文遵循科學性和獨立性的原則，在已有的相關研究成果［10，11］基礎上，從可靠性、經(jīng)濟性、適應性、環(huán)保性四個方面構建火電廠選址方案的綜合評價指標體系。

3 主成分分析法

主成分分析法(principal component analysis，PCA)是多元統(tǒng)計學中進行數(shù)據(jù)簡化降維的方法［12］。主成分分析法已經(jīng)成功地應用于電力系統(tǒng)負荷預測、故障診斷、穩(wěn)定評估等［13－15］領域中。PCA的基本原理是用少數(shù)幾個不相關的數(shù)據(jù)，來替代原有較多的相關數(shù)據(jù)，并且使新數(shù)據(jù)成為原有數(shù)據(jù)的一個線性組合。即所選的新數(shù)據(jù)被稱作主成分，選取主成分的原則是要盡量保留原數(shù)據(jù)中所含有的基本信息。利用統(tǒng)計學角度來分析，方差可以體現(xiàn)數(shù)據(jù)所含有的信息。方差越大，其數(shù)據(jù)所包含的信息量越大。

表1 綜合評價指標體系

設由m個決策方案、n個指標構成的綜合評價矩陣X=(xij)m×n，其中xij為方案i對于指標j的評價信息。利用公式(1)對指標信息進行標準化

式中:xj、Sj分別表示指標j的均值和標準差進行標準化處理后的指標數(shù)據(jù) A=(aij)m×n=(A1，A2，…，An)滿足:即標準化處理后的指標變量均值為0，方差為1。

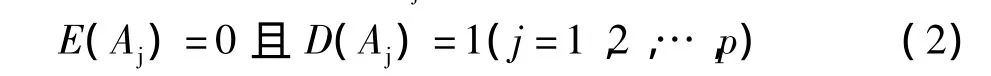
由標準化后的初始決策矩陣構建相關系數(shù)矩陣R= ( rij)p×p，系數(shù)矩陣的元素 rij表示指標 Ai和 Aj的關聯(lián)程度。

式中:cov(Ai，Aj)為指標Ai和Aj的協(xié)方差。根據(jù)公式(2)得到相關系數(shù)矩陣R與協(xié)方差矩陣相等。即相關系數(shù)矩陣為:

求出相關系數(shù)矩陣R的特征值，若R中有q個特征值大于零，特征值對應的特征向量為 P=(p1，p2，…，pq)，即主成分為:

將上式表示成矩陣形式:

主成分求解的具體理論證明可參考文獻［12］。它證明了主成分具有如下性質

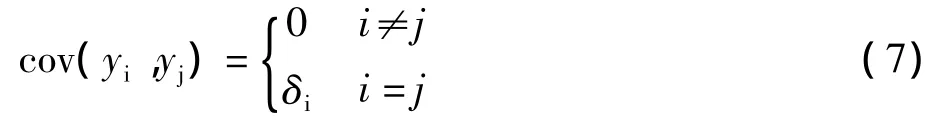
公式(7)表示主成分相互之間不關聯(lián)，且第i個主成分yi的特征值δi為該主成分的方式。第yi個主成分的方差對總方差的貢獻度:

貢獻度wi表示第i個主成分所蘊含的原始信息的百分比。因此第一主成分的方差貢獻度是最大的。這里定義前t個主成分的累積方差貢獻度γ為

為了使評價體系中數(shù)據(jù)結構盡量簡化，如果前t個主成分的累積方差貢獻度γ達到一定目標時，則將t個主成分代替原有評價信息的n個指標。由t個主成分來形成綜合評價函數(shù):

定義主成分的方差貢獻度為對應主成分的權重值。

3 基于主成分分析法的火電廠選址決策模型

建立主成分分析法的火電廠選址決策模型的過程:

(1)整理相關設計守則和規(guī)程，全面分析影響火電廠選址方案優(yōu)劣性的相關因素，并遵循科學性、系統(tǒng)性和獨立性的原則建立火電廠廠址候選方案綜合評價指標體系;

(2)構建火電廠選址方案的初始決策矩陣V=(vij)n×m;

(3)對初始決策矩陣進行標準化處理，得到標準化后的決策矩陣為A=(aij)m×n;

(4)計算指標信息的相關系數(shù)矩陣R;

(5)根據(jù)計算相關系數(shù)矩陣R的特征根和特征向量來確定主成分;

(6)計算累積方差貢獻度，選擇m個起主要作用的主成分來表示指標信息;

(7)將m個主成分與方差貢獻度形成綜合評價函數(shù)，計算各方案的綜合評價函數(shù)值并排序，得到最優(yōu)決策方案。

4 算例分析

本文以國內(nèi)某火電廠為例，先讓相關設計部門進行規(guī)劃設計初步確定三個候選廠址方案。通過各方案的實際數(shù)據(jù)進行統(tǒng)計得到經(jīng)濟性指標信息，采用專家評判法對剩下的指標進行打分并統(tǒng)計得到各指標的打分結果。各方案的評價矩陣如表2所示。

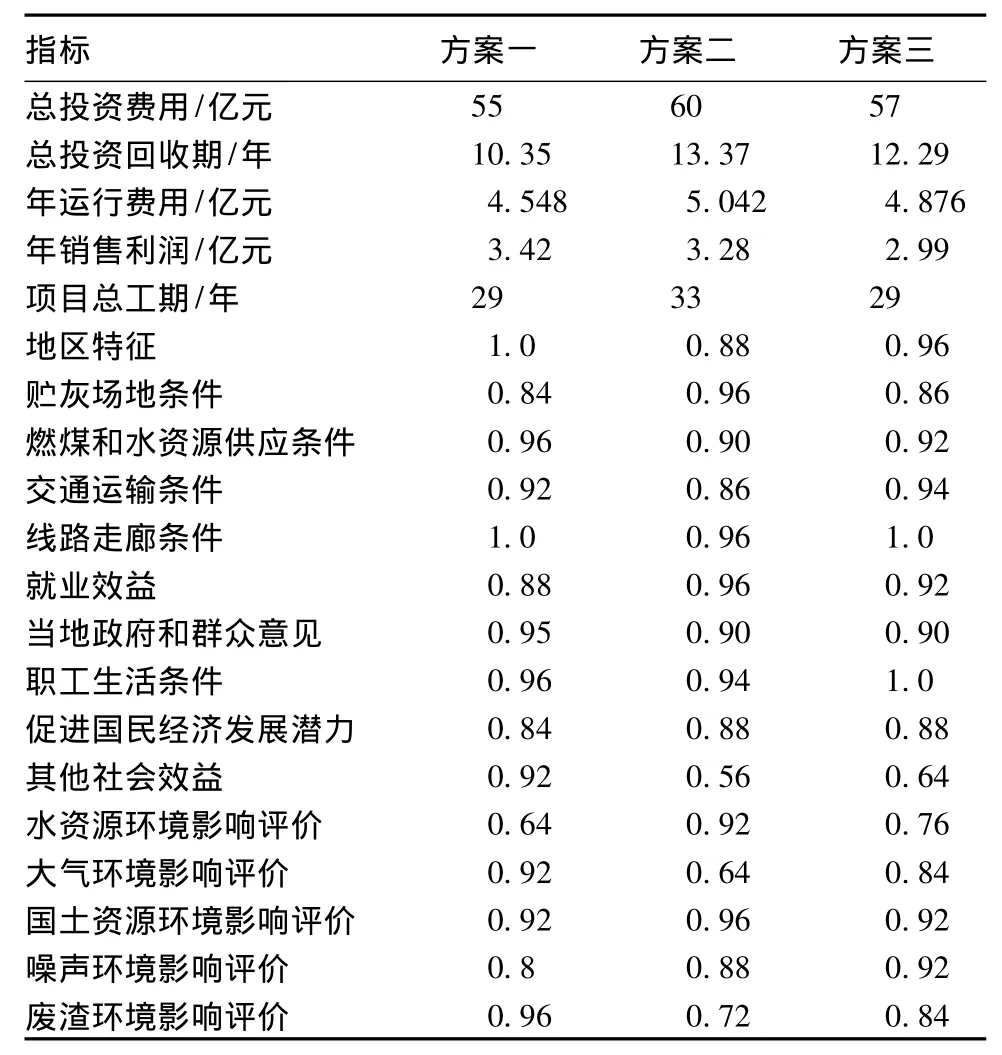
表2 各方案的評價矩陣

采用公式(1)對指標初始評價矩陣進行標準化處理。最終，得到標準化決策評價矩陣見表3。

表3 標準化的評價矩陣

再按照前文所述方法，利用公式(3)、(4)對標準初始化矩陣進行運算，得到相關系數(shù)矩陣R。相關系數(shù)矩陣R主對角線上的元素都是1，矩陣中多數(shù)元素絕對值都是大于0.75的，表明了各評價指標之間的相關程度較大。

由矩陣分析的相關知識，求取矩陣R的特征根

及對應的特征向量，求解得出矩陣R的兩個非零特征根，分別為 δ1=15.5047，δ2=4.4953，δ1與 δ2對應的特征向量分別為:

特征值δ1對應的方差貢獻度為77.52%，因此只需要用一個主成分y1來代替原來指標數(shù)據(jù)信息，由l1來構造主成分y1與原指標的線性組合關系

y1= －0.2535A1－0.2481A2－0.2467A3+0.0684A4－0.2263A5+0.2516A6－0.2415A7+0.2465A8+0.192A9+0.2263A10－0.2536A11+0.213A12+0.0956A13－0.213A14+0.2374A15－0.2538A16+0.2494A17－0.2263A18－0.1560A19+0.2536A20

主成分y1對應的方差貢獻度為77.52%，該主成分的權重為0.7752。最終的綜合評價函數(shù)為:

3個待決策方案的綜合評價函數(shù)值分別為2.9561、－3.1404、0.1844，顯而易見最優(yōu)火電廠選址方案為第一套方案。即候選廠址的優(yōu)劣順序為一、三、二。

模糊綜合評判法［5］和灰色層次分析法［7］計算該實例結果見表4。明顯地，兩種方法所得的最優(yōu)方案均為第一套方案，與本文模型所求結果一致。由于模糊綜合評判法中，隸屬度函數(shù)確定與最后的結果有很大的關系，而人為確定隸屬度存在著很大的主觀隨意性。灰色層次分析法在權重確定過程中也存在一定的主觀性。本文利用專家的經(jīng)驗和相關原始數(shù)據(jù)，構建了火電廠選址綜合評價指標體系，引入主成分分析法來建立模型，有效地避免了綜合評價過程中的人為主觀性，排序結果之間的區(qū)分度較大，使結果更加客觀、合理。

表4 其他方法評價結果

5 結論

本文對大型火電廠廠址選取的影響因素進行了分析和總結，將其細分為經(jīng)濟性指標、可靠性指標、適應性指標、環(huán)保性指標，在此基礎上，引入主成分分析法，建立了基于主成分分析的火電廠選址綜合決策的數(shù)學模型，通過實際算例進行驗證，并將模糊綜合評判法和灰色層次分析的結果與本文方法求得的結果進行了對比分析，驗證了本文模型的客觀性和有效性。本文所提方法思路清晰，計算簡單，便于編程實現(xiàn)。而且不需要主觀來確定權重，權重的確定完全依賴于客觀數(shù)據(jù)特征，減少了評判過程中的主觀因素和不確定因素，減少了電力決策者的工作量。

［1］楊勇平，劉殿海，楊昆，等.火電廠模糊優(yōu)化選址［J］.中國電機工程學報，2006，26(24):82 －87.

［2］吳耀武，侯云鶴，熊信艮，等.基于遺傳算法的電力系統(tǒng)電源規(guī)劃模型［J］.電網(wǎng)技術，1999，23(3):10 －14.

［3］馮凱，李遠德，侯云鶴，等.改進單親遺傳算法在電源規(guī)劃中的應用［J］.電網(wǎng)技術，2004，28(3):11 －15.

［4］賀峰，熊信艮，吳耀武.改進免疫算法在電力系統(tǒng)電源規(guī)劃中的應用［J］.電網(wǎng)技術，2004，28(11):38 －44.

［5］李艷梅，孫薇.多級模糊綜合評判在火電廠選址中的應用［J］.現(xiàn)代電力，2004，21(2):27 －30.

［6］梁冬青.基于熵權的模糊綜合評價方法在火電廠選址的應用［J］.煤，2010，19(1):3 －5，15.

［7］牛東曉.火電廠選址最優(yōu)決策中的灰色層次分析法［J］.電網(wǎng)技術，1994，18(6):27 －31.

［8］呂蓬，邢棉，康怡.火電廠選址最優(yōu)規(guī)劃中的層次分析法［J］.華北電力學院學報，1994，21(4):99 －105.

［9］郭新志，乞建勛，李星梅.基于改進模糊層次分析法的火電廠選址綜合評價方法研究［J］.現(xiàn)代電力，2007，24(3):67 －71.

［10］牛東曉，李建青，馬小勇.火電廠建設項目實施過程后評價指標體系研究［J］.華東電力，2010，38(9):1416 －1420.

［11］段利東，牛東曉，呂海濤.火電廠建設項目影響評價及其環(huán)境因素分析［J］.華東電力，2008，36(12):10 －12.

［12］余錦華，楊維權.多元統(tǒng)計分析與應用［M］.廣州:中山大學出版社，2005:193－197.

［13］劉寶英，楊仁剛.基于主成分分析的最小二乘支持向量機短期負荷預測模型［J］.電力自動化設備，2008，28(11):13 －17.

［14］黃保海，李巖，王東風.基于KPCA和KFCM集成的汽輪機故障診斷［J］.電力自動化設備，2010，30(7):84 －87.

［15］于之虹，郭志忠.改進主成分分析法用于暫態(tài)穩(wěn)定評估的輸入特征選擇［J］.電力自動化設備，2003，23(8):17 －21.