基于遺傳算法的電力系統無功優化

李文峰

(1.廣西大學電氣工程學院，廣西 南寧 530004;2.廣西興能電力建設有限公司，廣西 玉林 537000)

1 引言

電力系統無功優化控制是指在滿足各種電力系統運行條件的約束下，對系統進行盡量少的無功補償，使電力系統中的各個節點電壓得到最大限度的改善，系統的有功網損降低，達到提高電力系統運行穩定性與經濟性的目的［1］。它涉及選擇無功補償裝置地點、確定無功補償容量、調節變壓器分接頭和發電機機端電壓的配合等，是一個動態、多目標、多約束的非線性規劃問題，也是電力系統分析中的一個難題［2－5］。

無功功率的最優分布包括無功功率電源的最優分布和無功功率負荷的最優補償兩個方面［6］。電力系統的無功優化和電壓控制是相互作用的，合理的無功潮流分布是維持電壓穩定的前提。無功功率的流動將在電網中產生壓降，造成電力系統節點電壓偏移。當節點處的無功功率過剩時，往往意味著電壓的升高，相反，當節點處的無功功率不足時，常常會使電壓水平降低［7，8］。

電力系統無功優化與控制是保證電力系統安全經濟運行、提高電壓質量的重要措施，對指導調度人員安全運行和計劃部門進行電網規劃具有重要意義。電力系統無功優化與控制不僅能改善電壓質量，提高電力系統運行的穩定性，更能有效的減少網損，節約能源［9］。因此研究無功優化與控制問題具有重要意義。

2 牛頓法求解電力系統潮流

牛頓法是把非線性的方程式簡化為線性方程式，通過求解線性方程來得到原方程的近似解。線性化的過程如下:

設有非線性方程

設x(0)為該方程式的初值，則精確解x可表示為:

按泰勒級數展開:

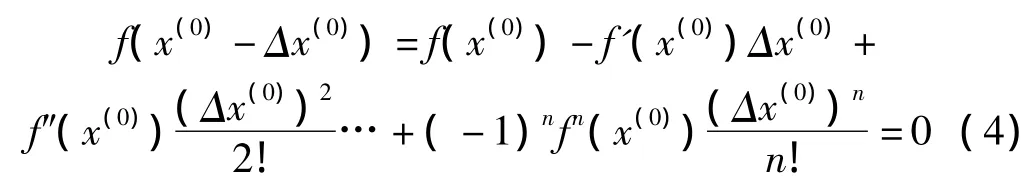
選擇的初值接近精確解時，Δx(0)很小，(Δx(0))2和更高次項可忽略不計，因此可化為:

這個方程稱為修正方程式，可以求出修正量Δx(0)。由于Δx(0)是由簡化公式求得，所以此時x=x(0)－Δx(0)不是精確解。可令:

將x(1)代入公式(5)，得:

這樣可以得到更加接近精確解的x(2):

如此不斷反復下次，就可以得到符合要求的近似解。

3 無功優化問題描述及其模型

在給定負荷和無功補償裝置地點的基礎上，以有功網損最小為目標函數，主要考慮了變壓器分接頭位置、并聯電容補償容量和發電機機端電壓的控制作用。這一類無功優化問題的數學模型如下:

①目標函數

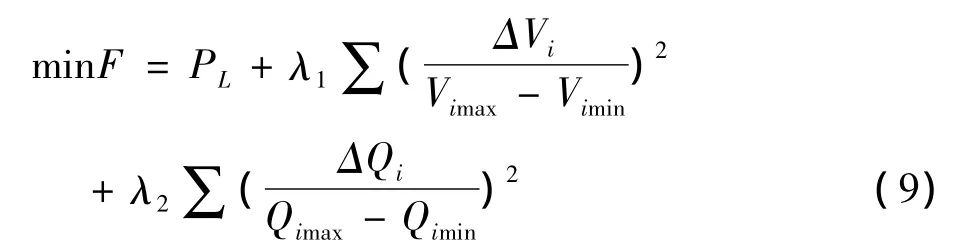
注:PL為有功網損;

λ2為對發電機無功功率越限的懲罰函數項;

②約束條件

等式約束條件:

注:Pi、Qi、Vi表示節點 i處注入的有功功率、無功功率和節點電壓;Gij、Bij、δij表示節點 i、j之間的電導、電納和電壓之間的相差角。

不等式約束條件:

注:Vimin、Vimax表示節點 i電壓的下上限;Qimin、Qimax表示發電機輸出無功功率的下上限;Timin、Timax表示變壓器變比的下上限;Cimin、Cimax表示并聯補償電容量的下上限;VGimin、VGimax表示發電機機端電壓的下上限;

4 遺傳算法無功優化解算

根據上面描述，基于遺傳算法的電力系統無功優化解算步驟如下:

(1)輸入網絡的原始數據、網絡的等式約束和不等式約束。

(2)將變量寫成碼的形式，編碼產生初始染色體域，其第一代染色體的產生可采用:Xi=INT［RND(Xmaxi－Xmini+1)］+Xmini，其中:RND為產生的唯一隨機數，其范圍為0≤RND≤1;INT為取整函數。

(3)計算每個染色體的適應函數值。

(4)用繁殖、交叉、變異三種遺傳操作完成在前代染色體域的基礎上產生新一代染色體域的工作。

(5)對進行遺傳操作后的第Ⅰ代染色體解碼后計算其適應函數值。

(6)若遺傳代數大于最先設定的最大遺傳代數，則結束循環。反之，返回(4)。

(7)安全約束的校驗包括狀態變量的等式和不等式約束，控制變量的范圍約束，如果控制變量和狀態變量中有違反約束的，仍需返回(4)。

(8)基于遺傳算法的電力系統無功優化問題收斂，獲得無功優化方案，染色體中適應度最好的為最優解，其次為次優，等等。

5 算例分析

本文采用IEEE 5節點數據為例，該系統拓撲如圖1所示。其中包含2臺發電機，分別在節點4、5處;2臺可調變壓器，分別在4－2、5－3的支路上;1臺無功補償設備，分別在節點3處。

圖1 IEEE 5系統

本文分別采用牛頓拉夫遜極坐標法和遺傳算法無功優化，運用matlab編程，對IEEE5節點系統進行了潮流計算。遺傳算法的計算過程中，參數設置如下:仿真代數T=60;群體規模M=40;交叉變異概率pm=0.1、pc=0.8;節點上下限 Vimax=1.1、Vimin=0.9;變壓器變比的上下限Timax=1.1、Timin=0.9;并聯補償電容量的上下限Cimax=0.05、Cimin=－0.05。

仿真結果如下:

圖2 常規潮流收斂曲線圖

圖3 最適應度進化曲線圖

表1 IEEE5系統潮流(節點電壓與網損)收斂結果/pu

遺傳算法優化后的結果如下:最優參數為:optxx=［1.0161 1.1000 －0.0016］;電壓最優適應度值為:bestv=4.4783。由表1可知，利用遺傳算法對IEEE5節點系統進行了無功優化計算，得到了較好的優化效果。

圖4 兩種模型電壓分布曲線

6 總結

電力系統無功優化是保證電力系統安全經濟運行、提高電壓質量的重要措施，對指導調度人員安全運行和計劃部門進行電網規劃具有重要意義。它涉及選擇無功補償裝置地點、確定無功補償容量、調節變壓器分接頭和發電機機端電壓的配合等，是一個動態、多目標、多約束的非線性規劃問題，也是電力系統分析中的一個難題。本文利用遺傳算法對IEEE5節點系統進行了無功優化計算，得到了較好的優化效果。

［1］許儀勛.基于遺傳算法的電力系統分層信息故障診斷方法研究［D］.哈爾濱:哈爾濱工業大學，2000，8(1).

［2］段玉倩，賀家李.遺傳算法及其改進［J］.電力系統及其自動化學報，1998，10(1)，12(3).

［3］徐唐煌.基于遺傳退火混合算法的配電網網絡重構研究［D］.武漢:華中科技大學，2005，14(6).

［4］馬晉，L.L.Lai，楊以涵.遺傳算法在電力系統無功優化中的應用［J］.中國電機工程學報，1995，15(3).

［5］倪煒，單淵達.具有優化路徑的遺傳算法應用于電力系統無功優化［J］.電力系統自動化，2000，24(21).

［6］陳皓勇，王錫凡.電力系統無功優化的退火選擇遺傳算法［J］.中國電力，1998，32(2).

［7］譚建成，王佩璋.電力系統無功綜合優化的模糊數學解法［J］.中國電機工程學報，1990，10(增刊).

［8］宋軍英，劉滌塵，陳允平.電力系統模糊無功優化的建模及算法［J］.電網技術，2001，25(3).

［9］程浩忠.基于遺傳算法的電力系統無功優化［J］.上海交通大學學報，1998，32.