導體棒在磁場中的轉動問題研究

黃濤

（宜城市第一高級中學 湖北襄陽 441400）

曹立鋒

（宜城市第三高級中學 湖北襄陽 441400）

導體棒在磁場中的轉動問題研究

黃濤

（宜城市第一高級中學 湖北襄陽 441400）

曹立鋒

（宜城市第三高級中學 湖北襄陽 441400）

用經典物理的方法研究了導體棒在磁場中的轉動規律，并用MathCAD2001軟件進行了數值模擬．

導體 磁場 轉動 求解數值 模擬

1 題目

如圖1所示，一半徑為R的半圓形光滑軌道豎直放置（導軌電阻忽略不計），以過最低點的向右切線為x軸，以豎直向上為y軸建立平面直角坐標系x Oy．在y＞0范圍內存在一垂直紙面向里的磁場，磁感應強度B與坐標值y成正比，即B＝ky（k＞0）．在半圓形軌道上有一根導體棒質量為m，電阻為r，導體棒所對的圓心角為α，導體棒左端與軌道的左端最高點對齊．當把導體棒由靜止釋放時，試分析導體棒的運動規律．

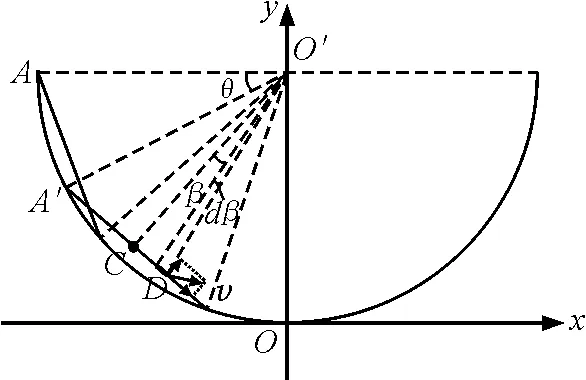
圖1

2 規律分析

2．1 導體棒的動力學方程

設某一時刻導體棒的A點轉過θ角，此時導體棒的角速度為ω＝，固定轉軸的剛體的動力學方程［1］

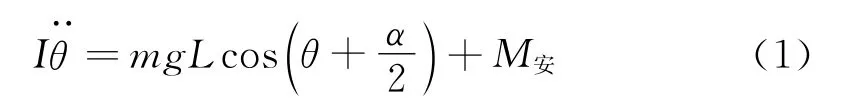
式（1）中I為導體棒的轉動慣量，α為導體棒所對的圓心角，L為導體棒中心到O′的距離為導體棒角加速度，M安為導體棒的安培力矩．

2．2 導體棒的轉動慣量［1］

2．3 導體棒的感應電動勢［2］

以棒的中點為界，下半部分與上半部分的切割速度方向相反，導體棒在圖示位置時，設質心的角速度為ω＝θ·，導體棒各點的速度在沿棒方向上的分量均為Lθ·，導體棒上的D點對應的磁感應強度為

根據對稱性可知導體棒的上半部分對應的電動勢為

2．4 安培力的合力矩

安培力的合力矩的方向為順時針方向與重力的力矩方向相反，所以導體棒的動力學方程為

由于導體棒的轉動慣量為

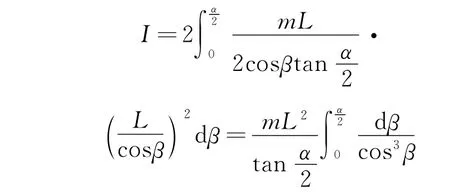
可得導體棒運動的微分方程

式中的兩個定積分可以查表［3］求出．

2．5 用MathCAD2001數值模擬

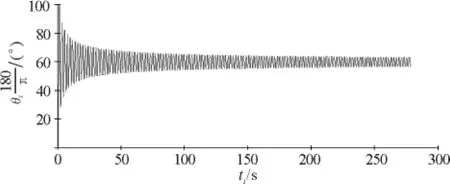
圖2 轉過的角度與時間關系圖

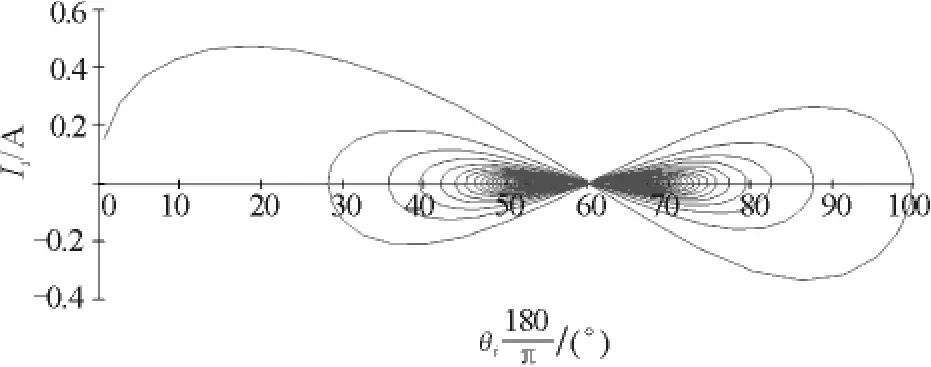
圖3 感應電流與轉過的角度的關系

圖4 導體棒的角速度與轉過的角度的關系

圖5 感應電流與時間的關系圖

3 圖像分析

由圖2和圖5可知導體棒的運動為阻尼振動，因為導體棒減少的機械能轉化為電能，所以它轉動的最大角度在減小，最后會停止在圓軌道的最低點，此時角度為60°；由圖3可知導體棒在運動到最低點的過程中，感應電流先增大后減小，再向右運動過程中感應電流反向先增大后減小，以后周而復始但最大電流在減小；由圖4可知導體棒在下降的過程中角速度先增大后減小，以后周而復始但最大角速度在減小．

1 周衍伯．理論力學教程（第二版）．北京：高等教育出版社，1997．186～188，173～175

2 趙凱華，陳熙謀．電磁學（下冊）（第二版）．北京：高等教育出版社，1997．479～485

3 四川大學數學系高等數學教研室．高等數學（物理類專業用第三版第一冊）．北京：高等教育出版社，1997．372～373

2014- 05- 05）