壁板邊界松馳下顫振非線性動力特性分析

肖艷平，楊翊仁，葉 露

（1.西南交通大學力學與工程學院，成都 610031；2.中國民航飛行學院飛行技術學院，廣漢 618307）

壁板邊界松馳下顫振非線性動力特性分析

肖艷平1，2，楊翊仁1，葉 露2

（1.西南交通大學力學與工程學院，成都 610031；2.中國民航飛行學院飛行技術學院，廣漢 618307）

采用分離變量法和伽遼金法建立三維壁板的非線性氣動彈性運動方程，用一階活塞理論模擬壁板所受的氣動力，分析了壁板的顫振邊界及穩定性，進而取邊界松弛因子，動壓和面內力為分叉參數，研究壁板顫振時的分叉及混沌等復雜動力學特性。計算結果表明：邊界松弛下壁板顫振系統表現出豐富的動力學行為，其分叉特性很復雜。隨著邊界松弛因子的增大，靜態穩定區域縮小，而屈曲和混沌區域增大，系統穩定性降低。

壁板；顫振；活塞理論；邊界條件；分叉

壁板顫振，是指高速氣流中壁板結構的慣性力、彈性力以及一個表面上的氣動力共同作用下產生的一種自激振動現象。雖然壁板顫振由于幾何非線性效應，一般不會像機翼顫振那樣發生振幅隨時間以指數形式增長的破壞性振動，而通常呈現出限幅極限環振動的形式，但是劇烈的壁板顫振對壁板結構的疲勞壽命甚至飛行器的飛行性能以及飛行安全產生十分不利的影響［1－3］。

壁板顫振系統動力特性十分復雜，隨著系統參數的變化，壁板表現出靜不穩定性（屈曲）和動不穩定性（顫振與混沌運動）。影響壁板顫振動力特性的系統因素有很多，其中重要一項就是支撐的邊界條件。常規情況下，研究壁板的動力特性總是假定支撐邊界是理想的，即邊界是簡支或固支的。實際上，邊界固定很難滿足這種理想的邊界，有很多的因素影響邊界條件，如選用材料機械性能的偏差，尺寸大小，裝配工藝差異，摩擦，墊圈蠕變等。另外，由于長時間的振動也會使邊界條件發生改變。這樣必然影響壁板的結構強度和疲勞特性。而對于邊界條件對壁板結構的影響的研究較少，還有待加強。夏巍等［4－6］采用有限元法對理想邊界條件（簡支和固支邊界）壁板的動力學特性進行了研究。Lindsley等［7－8］采用邊界扭轉彈簧，通過調節扭轉彈簧剛度的大小研究邊界扭轉剛度對壁板系統動力特性的影響。Ibrahinua［9－10］采用伽遼金法分析二維無限展長壁板相關邊界條件下非線性動力特性和和隨機特性。

本文以超音速流作用下的三維壁板為模型，運用Von Karman大變形非線性應變－位移關系和一階活塞氣動力理論，采用分離變量法和伽遼金法建立了三維壁板的顫振方程，再用Matlab編程進行了數值仿真，研究邊界條件對壁板動力特性的影響。

1 動力學方程

考慮一個受面內力Nx，Ny作用的三維壁板a×b× h，且h?a，單位長度質量為ρ。上表面作用有沿x方向超音速氣流，其速度為U∞，如圖1所示。根據Kirchhoff平板理論和Von Karman大變形定理，其控制方程為：

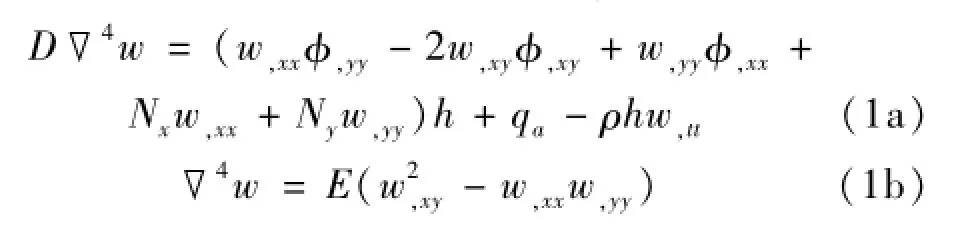
其中：w為板的z向位移，D＝Eh3／12（1－μ2）為板的彎曲剛度，φ為Airy應力函數，E為材料的彈性模量，q0為氣動載荷，▽2（）＝（），xx＋（），yy，下標中一撇表示對其后的變量求導數。在板的y方向上，由于板的兩邊都被簡支，又與來流垂直，高階模態不易激發，僅取其一階模態就可以體現此方向上的變形影響，故N取1。而在板的?方向上，為簡化分析，只取四階，即M取4。

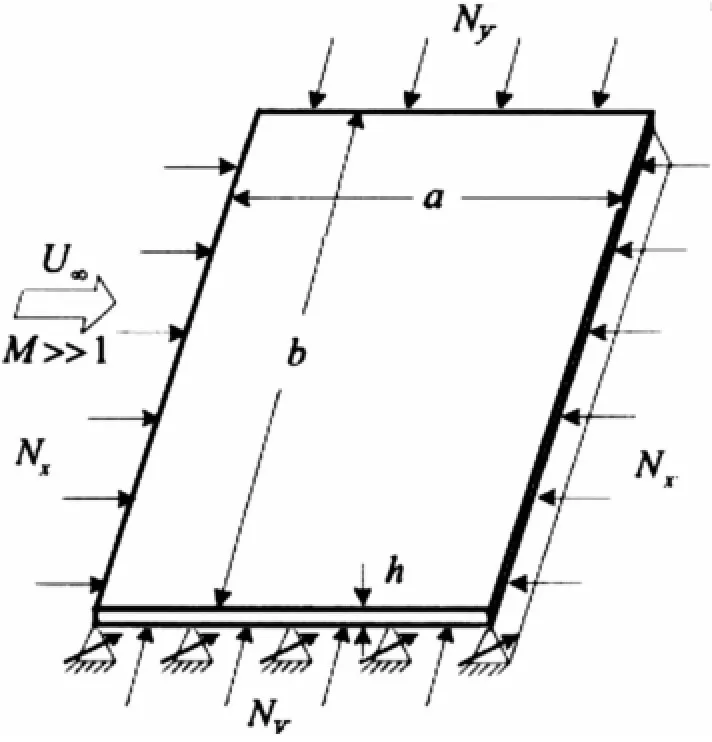
圖1 壁板模型Fig.1 Themodel of panel

2 氣動力

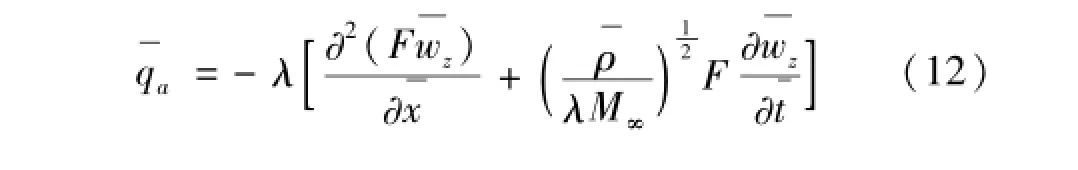
3 線性分析

線性顫振分析目的是為了確定系統的顫振邊界，即系統無量綱臨界動壓隨邊界松弛因子k的變化關系。令q＝eiΩt，代入式（9）的線性部分，可以得到系統的特征值矩陣，其中Ω通常情況為復數形式，Ω＝ω＋ci，ω為實部，即為系統頻率，c為虛部，表征系統的阻尼。取結構幾何參數sb＝1，sh＝300，質量參數／M∞＝0.01，面內力Rv＝Ry＝0，代入式（9）的線性部分，根據特征值計算結果得到系統的頻率ω與阻尼c隨無量綱動壓λ的變化，如圖2所示。實線和長短線分別表示理想的固支和簡支邊界條件。由圖可知：對于特定的k，當無量綱動壓λ＜λcr時，系統一階頻率隨動壓的增加而增大，系統阻尼全部都小于零，系統平衡點漸近穩定；當λ＝λcr時，第一階頻率與第二階頻率相交，系統失穩，此時阻尼等于零，系統平衡點失穩，即系統產生顫振。圖3給出了不同無量綱面內壓力R（R＝－Rx／π2）下顫振臨界動壓λcr隨邊界松弛因子k的變化曲線。由圖2可知k＝1與k＝∞時，系統的動態情況已經很接近，因此圖3和后面計算重點關注k變化區間為0～1。由圖3可知，k等于零（固支邊界）時的顫振臨界動壓λcr大于k大于零時的顫振臨界動壓λcr，邊界約束松弛減小了顫振臨界動壓，降低了系統的穩定性。另外，當面內壓力Rx增大時，穩定區域減小，而顫振區域在增大，面內壓力不利于壁板穩定。

4 非線性分析

基于Matlab編程，采用四階龍格－庫塔法對式（9）進行積分，得到模態坐標下的響應，再利用（3）式將其轉化到物理坐標下，即可得到壁板的最大位移處（＝0.75＝0.5）時間響應歷程。

4.1 穩定邊界

分別取五個不同的邊界松弛因子k，考察其對壁板動力學行為分布的影響。圖4給出了R－λ參數平面內系統的動力特性分布。從圖中可以看出，顫振系統在參數平面內表現出各種動力學行為，包括（Ⅰ）靜態平衡，（Ⅱ）靜態屈曲，（Ⅲ）極限環運動，（Ⅳ）擬周期和混沌。而邊界松弛因子的大小對顫振模型的動力學特性影響很大。當k增大時，靜態穩定區域縮小，而屈曲和混沌區域在增大。由此可見，邊界松弛降低了系統維持靜態穩定的能力，增加混沌運動的可能性。此結果與通過線性穩定性分析得到的結果吻合，但線性分析無法得到混沌區域的變化情況。

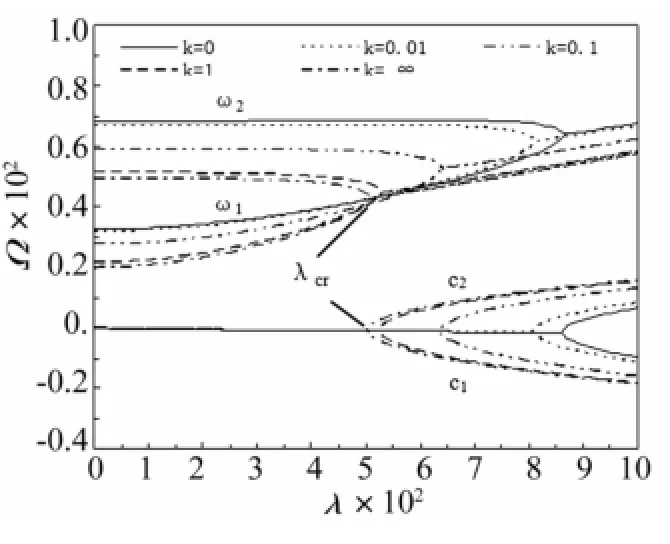
圖2 特征值隨動壓的變化圖Fig.2ωand c vsλfor different k

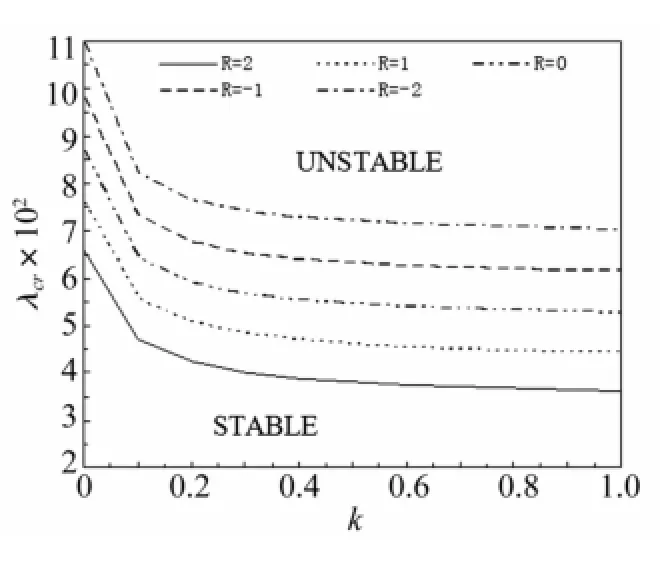
圖3 顫振臨界動壓隨邊界松弛因子的變化圖Fig.3λcrvs k for different R

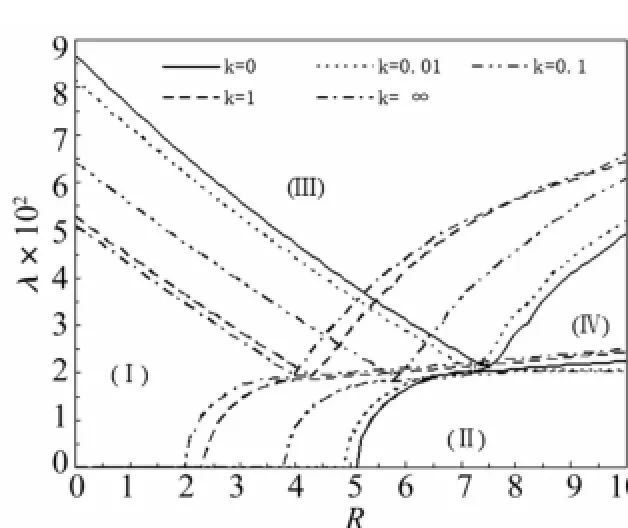
圖4 不同邊界松弛因子下正方形壁板穩定邊界Fig.4 Stability boundary for different values of relaxation parameter

4.2 k為分岔參數

將邊界松弛因子k作為可變參數，計算系統的分叉圖。對某個k值，當位置＝0.75＝0.5處達到穩態響應后，記錄速度為零的位移。改變k值，按上述過程便得到了離散無量綱位移隨邊界松弛因子k變化的分叉圖。取λ＝230，R＝5.7，邊界松弛因子k的變化區間為［0，1］，則無量綱位移隨k變化的分叉圖如圖5所示。隨k的增大，系統經歷了衰減振動狀態，周期1振動，周期3振動和擬周期振動后，又進入周期3振動，擬周期振動，隨后進入混沌狀態。繼續增大k值，系統再次進入周期3，最后由擬周期振動進入混沌運動狀態。

上面所述的現象通過相平面曲線來描述更為清楚。當k＜0.06時，平衡點為穩定的焦點，任何擾動經一段時間后將回到平衡點。當0.06≤k＜0.13時，系統處于簡單的極限環振動，如圖6（a）。當0.13≤k＜0.135，0.17≤k＜0.28和0.45≤k＜0.6時，系統處于周期3極限環振動，如圖6（c，f）；當0.135≤k＜0.17，0.28≤k＜0.325及時0.6≤k＜0.65，系統處于擬周期振動，如圖6（b，d，f）；當0.325≤k＜0.45與k≥0.65時系統處于混沌狀態，如圖6（e，h）。

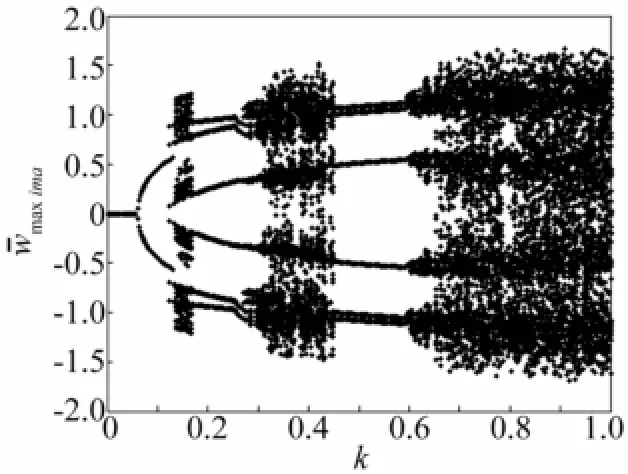
圖5 分叉圖；λ＝230，R＝5.7Fig.5 Bifurcation diagram forλ＝230 and R＝5.7

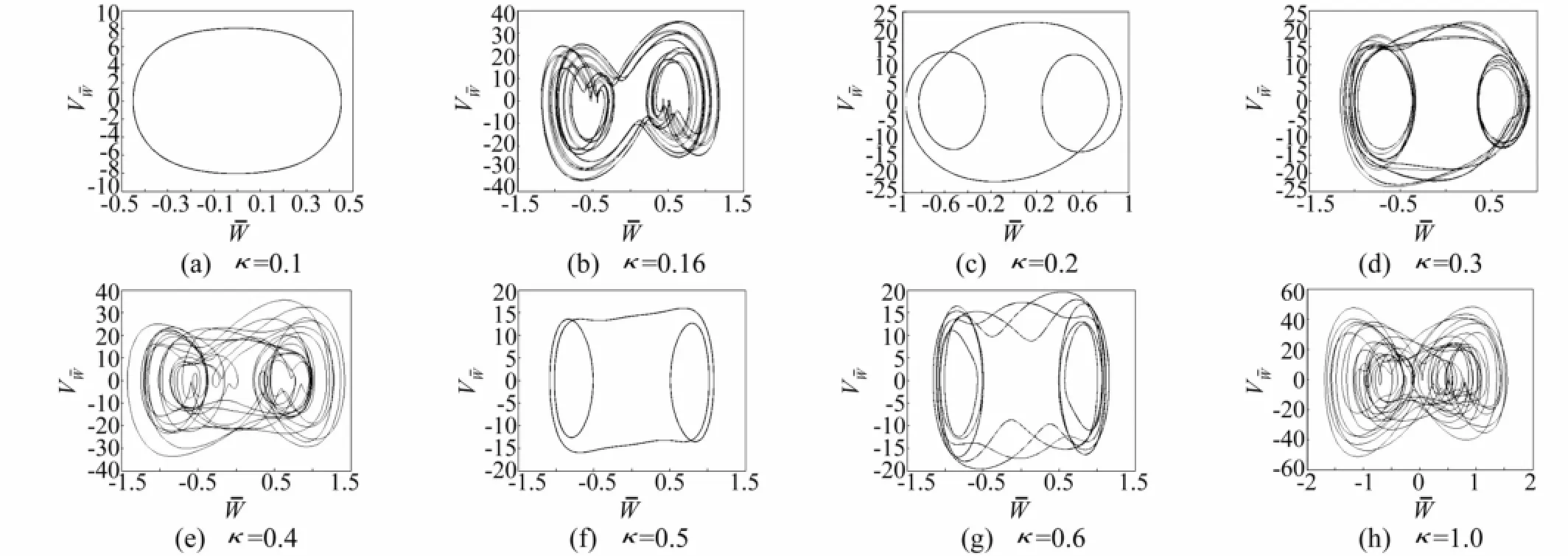
圖6＝0.75＝0.5處相圖，λ＝230，R＝5.7Fig.6 Phase－p lane plots wher＝0.75＝0.5 forλ＝230，R＝5.7

4.3 λ和R為分岔參數

取R＝5.7，k＝0.2，無量綱位移隨動壓變化的分叉圖如圖7所示。當λ＞184.5后，系統由屈曲狀態直接進入混沌狀態；當λ＞223.5后系統進入周期3振動，直到λ＝234.5系統再次進入混沌運動狀態。當λ＞276.5后，系統處于非對稱的極限環振動狀態，大振幅偏向壁板的哪一側是隨機的。當λ≥288后，系統進入對稱極限環振動狀態。圖8給出無量綱位移隨面內壓力變化的分叉圖（取λ＝230，k＝0.2）。隨面內壓力R的增大，系統經歷了衰減振動狀態，周期1振動（R≥4.57），周期3振動（R≥5.32），擬周期振動（R≥5.3），隨后又進入周期3振動（R≥6.33），擬周期振動（R≥6.56），最后進入混沌運動狀態（R≥6.63）。

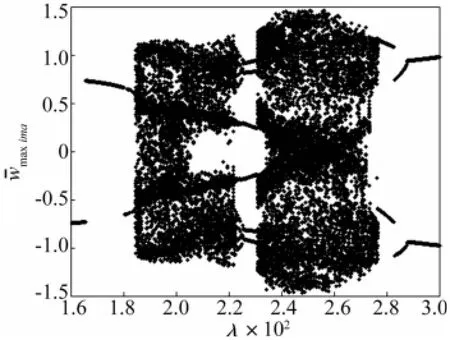
圖7 分叉圖；R＝5.7Fig.7 Bifurcation diagram for R＝5.7 and k＝0.2

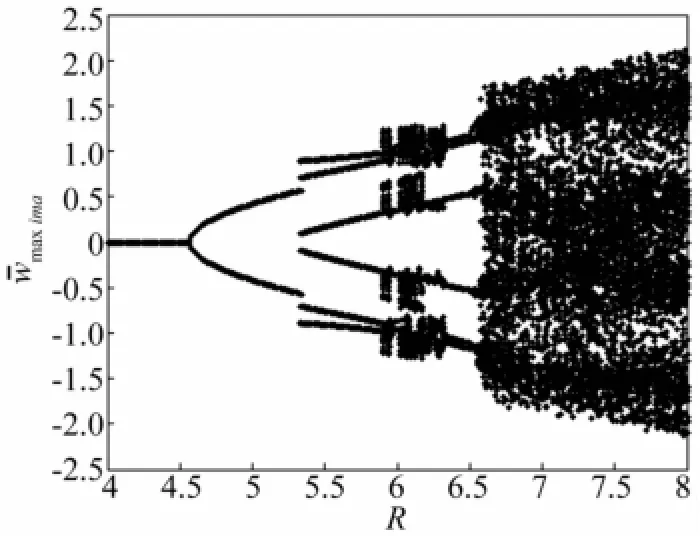
圖8 分叉圖；λ＝230，k＝0.2Fig.8 Bifurcation diagram forλ＝230 and k＝0.2

5 結 論

通過對邊界松弛下壁板顫振非線性動力特性的研究，可得出如下結論：

（1）線性理論分析表明邊界松弛減小了顫振臨界動壓，降低了系統的穩定性。

（2）考慮幾何大變形非線性時，通過分析顫振系統在邊界松弛下其運動特性在分岔參數平面內的分布，發現隨著邊界松弛因子的增大，穩定區域減小，而靜態屈曲區域和混沌運動參數范圍在增大，系統穩定性降低。通過對分叉圖及相圖分析可得，邊界松弛改變了系統顫振特性。

（3）當面內壓力增大時，穩定區域減小，而顫振區域在增大，面內壓力不利于壁板穩定。

［1］楊智春，夏 巍，孫 浩.高速飛行器壁板顫振的分析模型和分析方法［J］.應用力學學報，2006，23（4）：537－542.

YANG Zhi-chun，XIA Wei，SUN Hao.Analysis of panel flutter in high speed flight vehicles［J］.Chinese Journal of Applied Mechanics，2006，23（4）：537－542.

［2］Dowell E H.Nonlinear oscillations of a fluttering plate［J］.AIAA J，1966，4（7）：1267－1275.

［3］肖艷平，楊翊仁，葉獻輝.三維粘彈壁板顫振分析［J］.振動與沖擊，2011，30（1）：82－86.

XIAO Yan-ping，YANG Yi-ren，YE Xian-hui.Flutter analysis of a three-dimentional viscoelastic panel［J］.Journal of Vibration and Shock，2011，30（1）：82－86.

［4］夏 巍，楊智春.復合材料壁板熱顫振的有限元分析［J］.西北工業大學學報，2005，23（2）180－183.

XIA Wei，YANG Zhi-chun.Flutter analysis of composite panels with thermal effects［J］.Jounal of Northwestern Polytechnicao University，2005，23（2）：180－183.

［5］Mei C.A finite element approach for nonlinear panel flutter［J］.AIAA J，1997，35（8）：1107－1110.

［6］Cheng G F，Mei C.Finite element modal formulation for hypersonic panel flutter analysis with thermal effects［J］.AIAA J，2004，42（4）：687－695.

［7］Lindsley N J，Beran PS，PettitC L.Effects of uncertainty on Nonlinear Plate Response in Supersonic Flow［J］.AIAA Paper，2002－5600.

［8］Lindsley N J，Beran PS，Pettit C L.Effects of uncertainty on Nonlinear Plate Aeroelastic Response［J］.AIAA Paper，2002－1271.

［9］Ibrahima R A，Beloiua D M.Influence of joint relaxation on deterministic and stochastic panel flutter［J］.AIAA J，2005，43（7）：1444－1454.

［10］Beloiua D M，Ibrahima R A，Pettit C L.Influence of boundary conditions relaxation on panel flutter with compressive in-plane loads［J］.Journal of Fluids and Structures，2005：743－767.

Non linear dynam ic analysis for a panel's flutter w ith boundary condition relaxation

XIAO Yan-ping1，2，YANG Yi-ren1，YE Lu2
（1.School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China；2.School of Flight Technology，Civil Aviation Flight University of China，Guanghan 618307，China）

A nonlinear dynamic analysis for a panel's flutter with boundary condition relaxation was conducted here.The flutter differential equations of a three-dimensional panel were built by using separation of variables and Galerkin method.The first piston theory was employed to calculate the aerodynamic load on the panel.The flutter boundary and stability for the flat panelwere analyzed.Then，taking temperature，dynamic pressure and in-plane load as bifurcation parameters，their bifurcations and chaos behaviors were studied.The results demonstrated that the rich dynamic behaviors of the panelwith boundary condition relaxation and its complex dynamic characteristicswith variation of bifurcation parameters are revealed；both the buckling region and chaotic region increase with increase in relaxation of boundary conditions and the stability of the system decreases.

panel；flutter；piston theory；boundary condition；bifurcation

V214.3

A

中央高校基本科研業務費專項資金資助（2010Z707）項目；中國民航飛行學院面上項目（J2010－77）

2012－09－28 修改稿收到日期：2013－03－11

肖艷平女，博士生，講師，1980年生