基于RSSI的無線傳感器網絡節點定位算法研究*

蔡曉宇，張愛清，葉新榮

(安徽師范大學物理與電子信息學院，安徽蕪湖421000)

0 引言

無線傳感器網絡(WSN，Wireless Sensor Network)是指由大量成本低、尺寸小、低功耗、具有感知能力、計算能力、無線通信能力的傳感器節點組成的網絡［1］。其目的是協作地感知、采集和處理網絡覆蓋區內感知對象的信息并發送給觀測者［2］。WSN通過實現大規模環境檢測和追蹤任務，在軍事方面、環境監測、交通管理、災難拯救等眾多領域極具應用前景［1］。

在傳感器網絡的許多應用中，用戶關心的一個重要問題是:在什么位置或區域發生了特定事件。例如目標監測與跟蹤、水文、火災、潮汐、飛行器設計、智能交通、物流管理等許多應用都要求網絡節點提供自身的位置，并在通信和協作過程中利用位置信息完成應用要求。

現有的定位技術中，根據定位過程是否測量節點間的實際距離或角度，把定位算法分為基于測距技術的定位(Range－based)和無需測距技術的定位(Range－free)［3］。Range－ free定位則無須測量距離和角度信息，僅根據網絡連通性等信息即可實現，但定位精度較低。Range－based定位通過測量節點間點到點的距離或角度信息，使用三邊測量法(Trilateration)、三角測量法(Triangulition)或最大似然估計法計算節點位置。Range－based定位常用的測距技術有 RSSI(Received Signal Strength Indicator)、TOA(Time Of Arrival)、TDOA(Time Difference On Arrival)和 AOA(Arrival Of Angle)等［4］。Range －based定位算法由于其測距精度較高等優點使得其在較小規模或對精度要求較高的無線傳感器網絡中應用極為廣泛。文獻［5］中比較了上述4種常用的基于Range－based算法的定位技術［5］。結果給出，RSSI技術因其不需要額外硬件，容易實現且定位精度高等優點成為無線傳感器網絡節點定位技術中使用最廣泛的測距技術之一。RSSI技術利用已知發射信號強度和接收點根據收到的信號強度計算信號在傳播過程中的損耗，使用理論信號傳播模型或經驗模型將傳播損耗轉化為距離。在實際應用環境中，由于多徑、繞射、障礙物等因素，使得定位過程中產生距離誤差。如何消除或減小距離誤差是提高定位精度的關鍵。近幾年，許多研究人員致力于在特定環境下如何提高RSSI定位的精確度這一問題，取得了一定的成果。文中在研讀近5年有關文獻的基礎上，綜述了基于RSSI的無線傳感器網絡定位算法的原理模型和影響因素。總結了近幾年基于RSSI的無線傳感器網絡定位算法及改進算法。指出了基于RSSI的無線傳感器網絡節點定位算法的不足和研究方向。

1 RSSI定位原理

利用Range－based定位算法計算未知節點的過程可分為3個階段:測距階段、定位階段和修正階段［6］。具體過程描述如下:

1)利用RSSI技術，通過建立好的信號傳輸模型計算未知節點與鄰居節點間的距離。

2)利用數學模型計算出未知節點的位置坐標。

3)對估算出的未知節點的坐標進行修正，進一步提高算法的定位精度。

1.1 RSSI信號傳輸模型

RSSI使用的信號傳輸模型包括理論模型和經驗模型。經驗模型比較簡單多樣，它的一些參數取值可根據經驗選取，缺點是精度不高，多用于大致估計。下面重點介紹理論模型。

RSSI測距的理論模型主要有Free－Space模型、Two－Ray Ground Reflection模型和Shadowing模型［7］。其中 Free－Space模型和 Two－Ray Ground Reflection模型屬于圓形信號傳輸模型。由于信號在傳輸的過程中受環境影響使得信號傳輸模型各不相同，因此，具有綜合性的Shadowing模型應用比較廣泛。

Shadowing模型由兩部分組成:損耗模型(Pass Loss)和對數正態分布模型。損耗模型是用一個已知參考距離r0及r0上的接收功率PL(r0)預測出未知距離處r的平均接收功率PL(r)，其公式為

式中，n為路徑損耗系數，范圍在2到6之間且隨著障礙物的增多而增大。而對數正態分布模型反映的是在固定距離上，接收能量符合對數正態隨機變化，即如果以dB作為計量單位Shadowing模型滿足高斯分布。其公式為

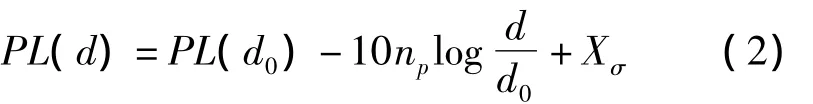
式中，PL(d0)為參考節點d0處的信號強度，PL(d)為在距離d處的未知節點的信號強度，np為路徑損耗系數。Xσ是標準差為σ的一個零均值的高斯隨機變量，對計算結果影響不大。

1.2 節點定位模型

1.2.1 三邊測量法

在二維空間中，由一個未知節點到3個或3個以上錨節點的距離，通過三邊測量法可以確定該未知節點的坐標。基本原理［8］是:求3個已知半徑和圓心坐標的圓的交點。如圖1所示，A(xa，ya)、B(xb，yb)、C(xc，yc)三點為已知節點坐標，D(x，y)為未知節點坐標。A、B、C三點到D點的距離分別為 da、db、dc，則有

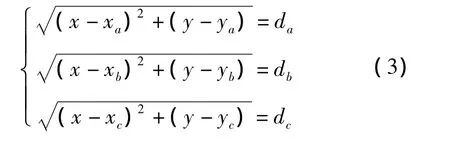
由式(3)解得D點坐標為

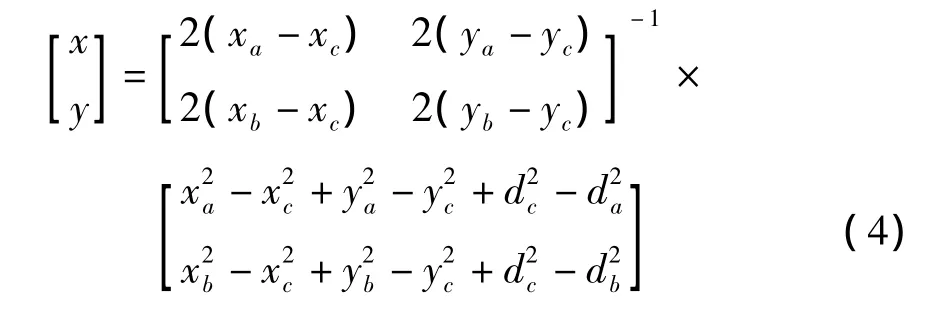
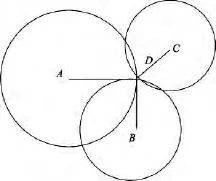
圖1 三邊測量法定位示意Fig.1 Schematic diagram of trilateration localization algorithm

1.2.2 三角測量法

三角測量定位方法也稱為信號到達角度(A0A)定位法或方位測量定位法［9］主要在測量信號到達角的時候使用。其基本原理［9］是通過未知節點接收器天線或天線陣列測出錨節點發射電波的入射角，從而構成一根從未知節點到錨節點的徑向連接，即為方位線。如圖2所示在二維平面中，利用兩個或更多錨節點的AOA測量值，按照AOA定位算法確定多條方位線的交點，即可計算出未知節點的估計位置。假設A(x0，y0)為未知節點，分別測得錨節點 B(x1，y1)、C(x2，y2)發出信號的到達角度為 θ1、θ2則有下式成立:

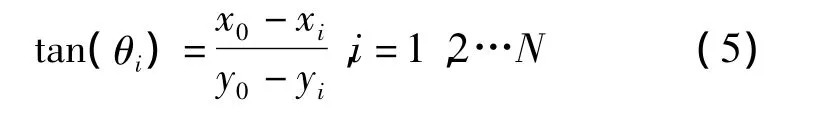
對式(5)進行求解可得未知節點A的坐標(x0，y0)。

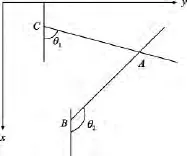
圖2 三角定位法示意Fig.2 Schematic diagram of triangulation localization algorithm

1.2.3 極大似然估計法

如圖 3 所示［10］，A(x，y)為未知節點，1，2，3，4…n為已知節點，當n＞3時有下式成立

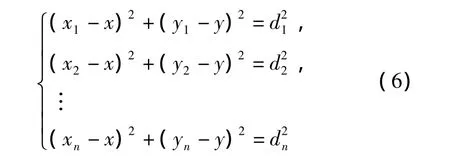
從第一個方程開始分別減去最后一個方程，求解得

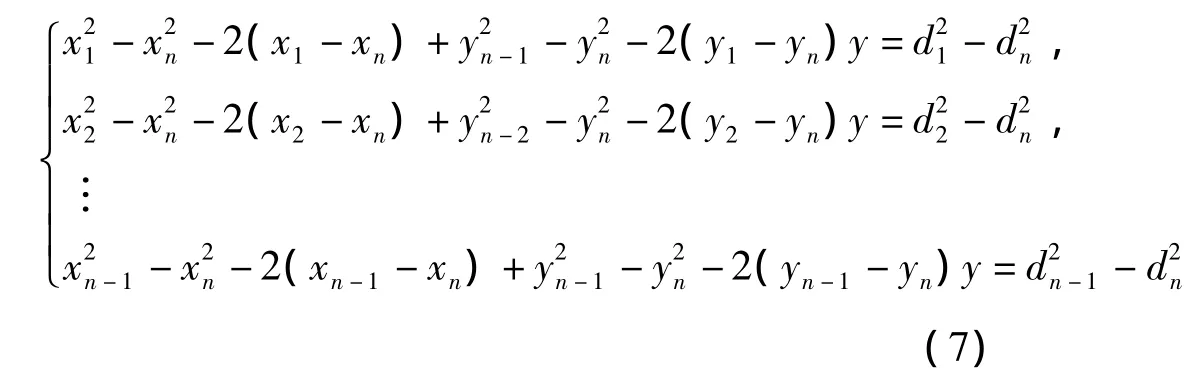
上式可用線性方程組表示為:AX=b，式中:

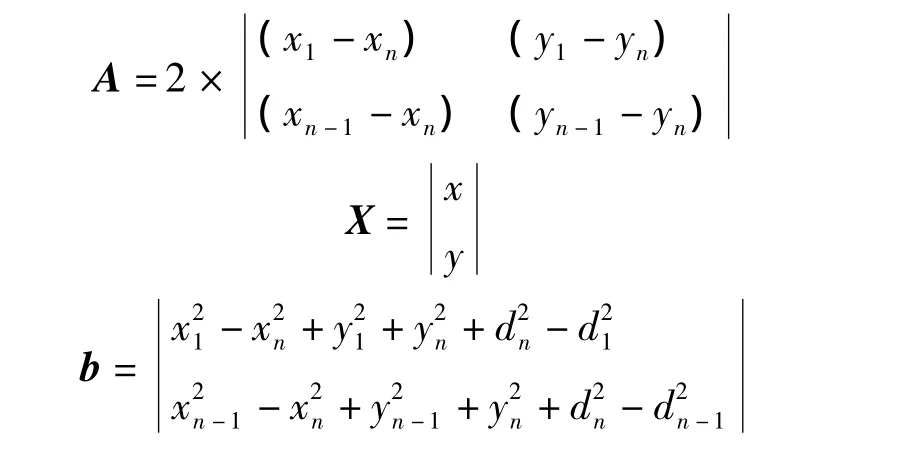
由此，可得到未知點坐標為

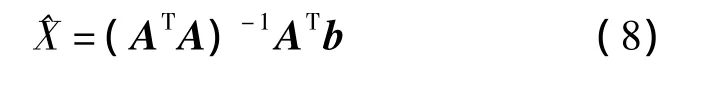
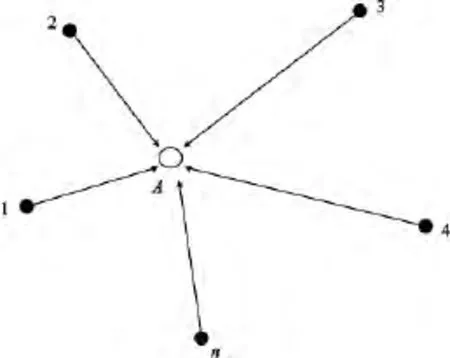
圖3 極大似然估計法定位示意Fig.3 Schematic diagram of the maximum likelihood method

1.3 RSSI測距技術的影響因素

實際應用中無線信號會受到溫度、濕度、障礙物等因素的干擾，使得測距精度受到影響，且不同的應用環境中干擾也各不相同。因此，研究這些障礙物對信號傳播的影響特性對提高定位精度有重要意義。

文獻［11］通過實驗驗證了無線信號接收強度和傳播距離之間存在確定的對數關系，且不同節點所受影響存在差異。實驗結果表明，RSSI的測量具有重復性和互換性，在應用環境下，RSSI適度的變化有規律可尋。

文獻［12］經過實驗驗證，溫度和濕度條件變化對無線信號傳輸的影響是沒有規律的，但影響效果不明顯。該文還指出，由于半導體工藝的原因，任何基于硅工藝的芯片都存在不同程度的溫度漂移，因此產生的白噪聲對射頻模塊有一定的影響。表1對影響RSSI測距精度的幾種因素做了比較。

表1 影響因素的比較Table 1 Comparisons of influencing factors

2 典型RSSI算法及其改進算法

本節將對基于RSSI定位算法及其改進算法進行總結。內容主要是從定位過程的三個階段即測距階段、定位階段和修正階段著手，分別從測距精度改進、定位精度改進和誤差修正改進等方面分析其改進算法的性能。

2.1 測距精度改進

文獻［13］考慮到電磁波受實際環境的影響造成RSSI測距誤差較大這一問題，提出了一種改進的測距算法模型。該模型從三個方面來抑制環境的干擾:首先利用最小二乘法曲線擬合構建實時測距模型。然后利用卡爾曼濾波處理RSSI值取得RSSI最優值。最后引入鏈路質量(LQI)結合RSSI實現分段處理。由此改進后的算法一定程度上克服了環境的干擾，提高了定位精度。

文獻［14］針對RSSI獲得信息的不穩定性，提出了一種參數糾正方案，實現了一種基于RSSI參數糾正的無線傳感器網絡應急救災系統。定位方法的實現分為兩步:

Step1通過路徑衰減因子η和陰影Xσ這兩個參數對測距模型表達式

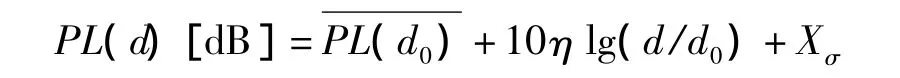
進行修正，并根據RSSI估算出節點之間的距離。文中給出η和Xσ的表達式為:

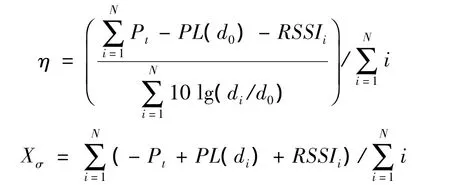
Step2部署多個信標節點，采用三邊測距定位法來實現被困人員的定位。

通過采用基于RSSI的參數糾正方法，消除了外界的各種因素干擾及累計誤差，從而提高了定位精度。

文獻［15］通過對現有無線傳感器網絡定位算法進行分析，引入立體式分層思想，提出了一種新的基于立體式RSSI的錨節點位置校正算法。該算法為了提高精度，提出了測距校正算法。改進的測距算法引入位置已知的種子節點做基準，之后逐步定位所有待測錨節點，并對錨節點進行位置矯正分析，從而構建未知節點定位網絡。RSSI測距校正模型步驟如下:

假設所有錨節點的坐標為(xi，yi)，待測節點坐標為(x，y)，結合周圍的錨節點就可以確定不同的圓:

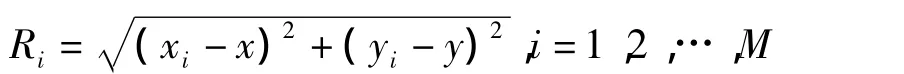
式中，M為網絡中錨節點數目。這些圓的交點就是待測節點的位置坐標，如圖4所示。

圖4 圓交點Fig.4 Circular intersection

相對于平面系統，被定位的待測節點將定位在任意兩個錨節點為交點的雙曲線上:

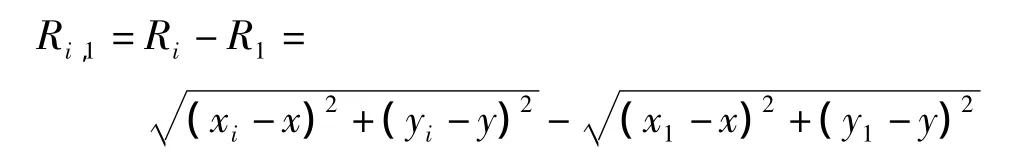
其中，i=2，3，…，M。把多個RSSI值組合在一起就能夠構成一組待測節點的雙曲線方程組，而通過求解該方程組就能得到待測節點的位置坐標。

RSSI的值由通信頻率以及接收器與發射器之間的距離決定［16］。由此，文獻［16］根據信號頻率對RSSI測量值的影響，提出一種新的基于RSSI測距改進算法。算法的思想是，用單一的收發器在保證通信距離不變的情況下發射不同頻率的電磁信號，測得各不相同的RSSI值，通過分析這些不同的RSSI值提高測距精度.

2.2 定位精度改進

質心算法［17］是通過未知節點接收所有在其通信范圍內的信標節點的信息，再將這些信標節點的幾何質心作為自己的位置來定位的一種算法。A(xa，ya)、B(xb，yb)、C(xc，yc)為 3 個信標節點，D(xd，yd)為盲節點。利用RSSI測的節點間距離相應為 da、db、dc，則盲節點 D 的坐標為

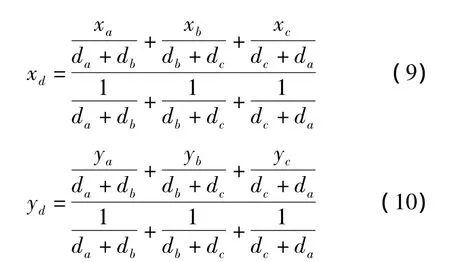
由于上述質心算法不能反映信標節點對未知節點的影響程度，針對這一問題，文獻［17］在上述質心算法的基礎上引入經優化后的加權因子，提出了一種優化的加權質心算法。文中給出的加權因子為利用加權因子可將式(9)、式(10)兩式變換為:

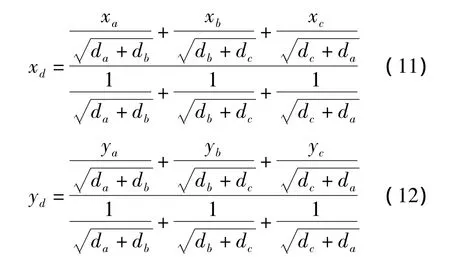
實驗結果表明，該優化后的加權質心算法不增加額外設備的情況下，在一定程度上提高了定位精度。

文獻［18］在基于三角加權定位的基礎上，引入四點定位的方法，提出了一種基于RSSI的ZigBee加權質心四點定位算法。改進后的方法對算法進行了可行性的優化，解決了基于三角加權質心定位硬件部署不易實現、精度不高的問題。

由于RSSI值受環境影響較大，測量距離往往帶來誤差，測距的誤差會直接降低定位精度，針對這種不足，文獻［19］提出一種RSSI－神經網絡定位方法，該方法的定位過程是首先建立數據采集模型，然后建立未知節點的RSSI值與坐標的映射關系，最后用神經網絡進行定位。神經網絡的定位主要分為兩個階段即學習期和工作期，學習期的任務是將訓練樣本帶入網絡對連接權值進行修正，工作期時網絡中的權值已經固定，網絡達到穩定，此階段可以根據不同的輸入得到輸出結果。

文獻［20］所提出的基于RSSI測距誤差修正的加權質心定位算法中的定位階段采用了改進Euclidean加權質心定位算法。如圖5所示，D(x，y)是未知節點，A、B為信標節點，當D接收到A、B發出的定位信號時，由RSSI值可得到距離dDA、dDB，同時得到兩三角形ΔD1AB和ΔD2AB，D1、D2為未知節點D的兩個可能位置;當增加信標節點C時，可測的dDC;比較的大小，值小的為未知節點D的位置(x1，y1);同理，取邊BA和 AC得到另外兩個估計位置(x2，y2)和(x3，y3)，通過計算三個近似位置(x1，y1)，(x2，y2)，(x3，y3)的質心，便可求的未知節點D(x，y)。

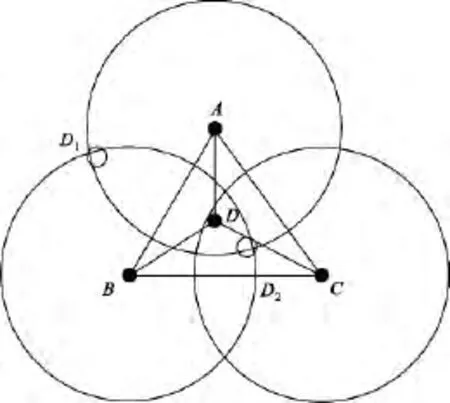
圖5 Euclidean改進算法示意Fig.5 Schematic diagram of Improved Euclidean algorithm

2.3 誤差修正改進

針對煤礦井下無線傳感器網絡節點定位精度低、誤差大的問題，文獻［8］提出一種基于RSSI的衰減校正因子的三邊加權質心定位算法。算法的基本思想是首先通過對RSSI衰減測量值補償校正，使其近似接近節點間實際真實值，衰減校正因子為Δd=(Δd1+φ(d))/2;然后取任意的三點的校正距離通過三邊測量法算出未知節點的RSSI測距估計值;最后對估計值進行加權質心處理得到未知節點估計坐標。文中給出未知節點的坐標估計值為():

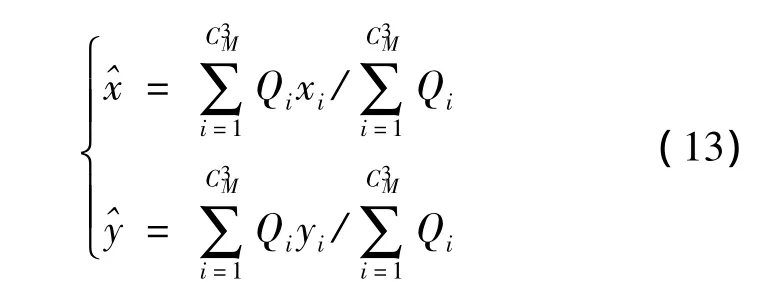
實驗驗證，該算法在不增加硬件設備的條件下，提高了定位精度和穩定性。

Ecolocation［21］是一種基于 RSSI的定位技術，其定位過程描述如下:

Step1定位計算節點(一個專用節點，可兼作錨節點)對錨節點發來的RSSI測量值進行處理，構造一個與序列排序有關的未知節點二維約束表Mα×α(α為錨節點個數)。

Step2定位計算節點對定位空間中的每一個格點分別計算它們與錨節點的歐式距離d，將得到的值按大小關系排序進而得到每個格點相對于錨節點的序列值及對應的二維約束表Cα×α。

Step3依次搜索每個格點的二維約束表數據，從中尋找與未知節點二維約束表數據匹配程度最好的格點，若有多個，取其質心作為未知節點的定位坐標。

上述定位算法中，由于射頻信道多徑及陰影效應導致的非理想特性和直接比較的不合理性，測量的數據往往會產生隨機誤差，進而影響定位精度。為彌補上述缺陷，文獻［21］從兩個方面進行改進:首先均采用RSSI值并統一約束表中的數據源;其次以未知節點的源數據為比較基準統一序列排序比較對象。實驗結果顯示，改進后的算法在無需額外增加硬件開銷的條件下，明顯改善了節點定位精度，但計算節點的復雜度也有所增加。

文獻［22］考慮道靜態權重算法不能同時解決定位的平均誤差和最大誤差的缺陷，提出一種新的結合RSSI測距數據處理的高斯擬合動態權重定位算法GFDWCL。GFDWCL算法的核心思想是首先對RSSI測量值做高斯擬合，找出密度最大的波峰值，濾除很大一部分錯誤的數據以減少一些小概率、大干擾事件對整體測量的影響，其次對靜態權重定位算法中的權重值的選取通過劃分區域和增加H門限值來約束，對不同的區域采用不同的權重值，以保證最小誤差。由此改進后的GFDWCL算法在能耗、平均誤差、最小誤差和最大誤差方面較靜態權重定位算法相比都有下降，定位穩定性也改善許多。

文獻［23］研究分析了在實際應用環境中，導致RSSI測距產生誤差的兩大因素:一是RSSI信號傳播理論模型參數誤差;二是障礙物阻擋時RSSI測距誤差。針對這兩大因素，文獻提出了RSSI信號理論模型在線修正方法及使用3個網絡節點來實現定位的新算法。算法思想分別為:①針對理論模型產生的誤差，采用局部TDOA輔助標定RSSI參數;②針對障礙物阻擋所產生的誤差，采用去除相鄰節點間距離最大值的方法(共三個距離)，來減小誤差。仿真實驗表明，該算法在應對較小尺寸的障礙物時，其性能非常可靠、穩定。表2對上述改進算法在改進內容和改進方法方面做了對比。

表2 幾種改進算法的比較Table 2 Comparisons for improved algorithms

3 結語

文中對現有的基于RSSI的無線傳感器網絡定位算法及改進算法進行了總結與概述，現有RSSI定位算法主要研究如何降低定位成本和提高定位精度。具體來說，集中在提出適應特定環境的低成本，高精度，高覆蓋和高魯棒性的定位方法。盡管上述每個算法都在各自適應的領域取得了良好的定位效果，但整體來看基于RSSI的定位算法仍然存在某些不足:①盡管RSSI定位技術不斷改進，但尚未找到能夠達到理論極限的定位算法，這使得定位過程中，隨著定位距離的加大，誤差會積累，不利于大范圍定位，最終使得算法可用性降低;②目前對RSSI定位算法的改進研究只是建立在仿真實驗的基礎上，對實際應用中可能存在的問題無法獲知，這大大限制了對RSSI定位算法的改進研究;③仿真實驗所用節點大都為靜態節點，實際應用中節點可能是運動的;④文獻中的仿真實驗大都是在二維空間定位，應拓展到三維空間。

綜上所述，經過研究者們近十年的研究，基于RSSI的定位算法取得了豐富的研究成果，特別是隨著科技的發展，WSN的自身定位問題有了更多的解決方案，但隨著研究工作的進展，需要我們解決的問題越來越多。可能的熱點研究方向包括:①線性傳感網絡環境下三維節點的定位;②錨節點成本較普通節點高兩個數量級［3］，因此，可研究關于無錨節點的定位算法;③文獻［22］提出的GFDWCL算法是以提高復雜度為代價降低功耗和誤差，所以定位算法復雜度與能耗之間如何達到最優也是未來研究的方向;④近幾年定位算法的研究主要集中靜態網絡，網絡中動態未知節點的定位算法將是未來研究重要方向。

［1］王偉，王華奎.基于RSSI無線傳感器網絡的Sybil攻擊檢測技術研究［J］.太原理工大學學報，2011，42(01):25－29.WANG Wei，WANG Hua － kui.Research on RSSI －based Sybil Attack Detection for Wireless Sensor Networks［J］.Journal of Taiyuan university of Technology，2011，42(01):25－29.

［2］田增山，羅磊，何維，等.一種分布式無線傳感器網絡節點定位算法［J］.傳感技術學報，2009，22(03):387 －390.TIAN Zeng － shan，LUO Lei，HE Wei，et al.A Distributed Node Location Algorithm of Wireless Sensor Network［J］.Chinese Journal of Sensors and Actuators，2009，22(03):387－390.

［3］王福豹，史龍，任豐原.無線傳感器網絡中的自身定位系統和算法［J］.軟件學報，2005，16(05):857 －868.WANG Fu － bao，SHI Long，REN Feng － yuan.Self－ Localization Systems and Algorithms for Wireless Sensor Networks［J］.Journal of Software，2005，16(05):857 －868.

［4］陳昌祥，達維，周潔.基于RSSI的無線傳感器網絡距離修正定位算法［J］.通信技術，2011，44(02):65－66.CHEN Chang － xiang，DA Wei，ZHOU Jie.RSSI－ based Range Collation Localization Algorithm in WSN［J］.Communications Technology，2011，44(02):65 －66.

［5］陳智勇，王健，季曉勇.無線傳感器網絡定位算法的研究進展.電子測量技術［J］.2010，33(10):40 －43.CHEN Zhi－yong，WANG Jian，JI Xiao － yong.Research on Location Algorithms in Wireless Sensor Networks［J］.Electronic Measurement Technology，2010，33(10):40 －43.

［6］舒展鵬.基于RSSI的無線傳感器網絡定位算法研究［D］.南京:南京郵電大學，2012.SHU Zhan － peng.Research on Node Localization Algorithm based on RSSI in Wireless Sensor Networks［D］.Nanjing:Nanjing University of Posts and Telecommunications，2012.

［7］馮愛麗，喬鋼柱，曾建潮.基于信標節點間距離的改進RSSI定位算法［J］.太原科技大學學報，2012，33(01):6－9.FENG Ai－ li，QIAO Gang － zhu，ZENG Jian － chao.Improved RSSI Location Algorithm based on Distance Between Beacon Nodes［J］.Journal of Taiyuan University of Science and Technology，2012，33(01):6 －9.

［8］龍鐵光，黃廷磊.無線傳感器網絡中基于RSSI算法的優化［J］.計算機系統應用，2013，22(01):107 －110.LONG Tie － guang，HUANG Ting － lei.Optimization of RSSI Algorithm in Wireless Sensor Network［J］.Computer Systems＆ Applications，2013，22(01):107－110.

［9］熊小華，何通能，徐中勝等.無線傳感器網絡節點定位算法的研究綜述［J］.機電工程，2009，26(02):13 －17.XIONG Xiao－ hua，HE Tong－ neng，XV Zhong － sheng，et al.Review on Localization Algorithms for Wireless Sensor Networks［J］.Mechanical＆Electrical Engineering Magazine，2009，26(02):13 －17.

［10］韓江洪，祝滿拳，馬學森，等.基于RSSI的極大似然與加權質心混合定位算法［J］.電子測量與儀器學報，2013，27(10):937 －943.HAN Jiang－hong，ZHU Man－quan，MA Xue－sen，et al.Hybrid Localization Algorithm of Maximum Likelihood and Weighted Centroid based on RSSI［J］.Journal of Electronic Measurement and Instrument，2013，27(10):937－943.

［11］方震，趙湛，郭鵬，等.基于 RSSI測距分析［J］.傳感技術學報，2007，20(11):2526 －2530.FANG Zhen，ZHAO Zhan，GUO Peng，et al.Analysis of Distance Measurement based on RSSI［J］.Chinese Journal of Sensors and Actuators，2007;20(11):2526 －2530.

［12］杜亞江，康雁林，郭佑民.基于RSSI的無線傳感器網絡節點測距方法研究［J］.工業控制計算機，2012，25(10):91－92.DU Ya－jiang，KANG Yan － lin，GUO You － min.Node Ranging Method based on RSSI of Wireless Sensor Network［J］.Industrial Control Computer，2012，25(10):91－92.

［13］徐登彩，周奇年，張振浩.基于RSSI測距算法改進的研究［J］.工業控制計算機，2013，26(05):72 －75.XU Deng －cai，ZHOU Qi－ nian，ZHANG Zhen － hao.Research on Improved Localization Algorithm based on RSSI［J］.Industrial Control Computer，2013，26(05):72 －75.

［14］凡高娟，侯彥娥，王汝傳.基于RSSI參數糾正的無線傳感器網絡應急救災系統［J］.鄭州大學學報，2012，33(04):94－97.FAN Gao － juan，HOU Yan － e，WANG Ru － chuan.RSSI based Parameters Correction Emergency Disaster Response System of Wireless Sensor Networks［J］.Journal of Zhengzhou University，2012，33(04):94 －97.

［15］關博，東超，弭洪濤.立體式RSSI無線傳感器網絡定位算法［J］.北華大學學報，2013，14(01):112 －116.GUAN Bo，DONG Chao，MI Hong － tao.Localization Algorithm of Wireless Sensor Networks 3D － RSSI［J］.Journal of Beihua University，2013，14(01):112 －116.

［16］CEYLAN O，TARAKTAS K F，YAGCI H B.Enhancing RSSI Technologies in Wireless Sensor Network［C］//International Conference on Broadband，Wireless Computing，Communication and Applications，2010.

［17］張正華，戴磊，黎家文，等.基于RSSI的優化加權質心定位算法研究［J］.電子設計工程，2013，21(07):171－173.ZHANG Zheng － hua，DAI Lei，LI Jia － wen，CHEN Hang.Research on Optimization Weighted Centroid Localization Algorithm based on RSSI［J］.Electronic Design Engineering，2013，21(07):171 －173.

［18］馮東棟，鄭文奎.基于RSSI的加權質心四點定位算法［J］.河南大學學報，2013，43(04):455 －458.FENG Dong － dong，ZHENG Wen － kui.Weighted Centroid Four Points Localization Algorithm for ZigBee Based on RSSI［J］.Journal of Heinan University，2013，43(04):455－458.

［19］孫健，杜永貴.RSSI－神經網絡在無線傳感網絡定位中的應用［J］.科學技術與工程，2013，13(06):1479 －1482.SUN Jian，DU Yong －gui.Applications of RSSI－neural Network in Wireless Sensor Network Positioning［J］.Science Technology and Engineering，2013，13(06):1479 －1482.

［20］劉曉文，關維國，鄒德君，等.基于RSSI測距誤差修正的加權質心定位算法［J］.電腦知識與技術，2012，08(01):126－129.LIU Xiao－ wen，GUAN Wei－ guo，ZOU De － jun，et al.The Algorithm of Weighted Centroid Localization Based on RSSI Distance Measurement Error Correction［J］.Computer Knowledge and Technology，2012，08(01):126－129.

［21］周永錄，代紅兵.基于RSSI的無線傳感器網絡定位算法研究［J］.云南大學學報，2011，33(S2):202 －205.ZHOU Yong－lu，DAI Hong－bing.Study of Localization Algorithm based on RSSI for WSNs［J］.Journal of Yunnan University，2011，33(S2):202 －205.

［22］詹杰，劉宏立，劉述鋼.基于RSSI的動態權重定位算法研究［J］.電子學報，2011，39(01):82 －88.ZHAN Jie，LIU Hong － li，LIU Shu － gang，et al.The Study of Dynamic Degree Weighted Centroid Localization Algorithm Based on RSSI［J］.Acta Electronica Sinica，2011，39(01):82 －88.

［23］陳三風，陳萬明.基于RSSI誤差分析的無線傳感器網絡定位研究［J］.計算機工程與應用，2011，47(14):10－12.CHEN San － feng，CHEN Wan － ming.Localization Algorithm based on Analysis of RSSI Error for Wireless Sensor Networks［J］.Computer Engineering and Applications，2011，47(14):10 －12.