散斑干涉相位條紋圖的頻域濾波處理

王永紅，李駿睿，孫建飛，劉 佩，楊連祥，2

(1.合肥工業大學儀器科學與光電學院，安徽合肥230009;

2.美國奧克蘭大學機械工程系，密歇根羅切斯特48309)

1 引言

散斑干涉測量技術利用激光散斑作為位移信息的載體，對物體的表面形變、位移、震動進行測量，是一種非接觸、測量精度高的實時全場光學測量技術［1-3］。利用時間相移技術［4-5］生成的干涉相位條紋圖被包裹于［－π，π］之間，為了獲得真實的相位分布，需要進行相位解包裹計算。但是生成的包裹相位圖含有大量的噪聲，嚴重影響了相位解包裹的結果和精度，甚至會因噪聲過大而造成相位解包裹的失敗。圖1(a)為利用時間相移技術得到的一幅原始包裹相位圖像，可以看出圖中存在大量的散斑噪聲。圖1(b)為其沿x軸截面上的相位分布圖，從圖中可以看出，此時的相位圖含有大量的噪聲干擾，這樣的相位圖無法實現解包裹處理。因此，在相位解包之前，需要對包裹的相位圖進行濾波去噪處理。如何有效地去除條紋圖的散斑噪聲成為電子散斑干涉測量技術的關鍵問題。

圖1 原始相位圖及x向相位分布Fig.1 Raw phase map and phase distribution in x direction

圖2 傳統濾波效果圖Fig.2 Filtered phase map using conventional methods

近年來國內外許多學者做了大量的研究工作，如中值濾波、均值濾波、傅里葉變換濾波等［6-8］傳統的濾波方法，在濾掉散斑噪聲的同時，也會濾掉、模糊許多有用的信息。如均值濾波丟失了原始相位圖中的相位跳變信息和“尖峰”信息，模糊了條紋的邊界(見圖2(a))。中值濾波雖然保留了相位跳變信息(見圖2(b))，但是由于基于雙側指數函數的噪聲統計分布假設，對于噪聲水平高的場合并不適用，且需要對濾波窗口中每個像素值的大小進行排序，計算時間較長;Annalisa Capanni等人提出了改進的中值濾波法［9］，但存在誤判現象;H.A.Aebischer等人提出正余弦濾波方法，保留了圖像中的“尖峰”信息［10］;秦玉文等人提出一種基于回歸算法的條紋濾波技術［11］;楊磊等人提出一種基于殘差點的干涉相位圖自適應濾波方法［12］;于起峰等人提出一種帶門限的旋濾波方法［13］，但是這些方法僅通過選取直線窗口內數據求均方差值進行比較判別，因此它受到噪聲的影響較大;當圖像的噪聲水平較高時，必須去較大的窗口才能消除噪聲;王開福等人提出一種基于同態濾波原理的條紋濾波方法，對相位圖去噪的同時可以增強圖像的對比度［14］;李凱等人提出一種基于 Gabor濾波的平滑方法［15］等。本文采用一種條紋正余弦分解和頻域濾波結合的方法，可以更好地提高濾波的精度和速度。實驗研究證明，與傳統的圖像降噪方法對比，，這種分解頻域濾波方法能夠在保留圖像“尖峰”信息的基礎上，較好地濾除圖像中的散斑噪聲，方法簡單有效。

2 條紋頻域濾波原理

圖像處理方法可以分為空域分析法和頻域分析法。空域分析法主要是對圖像矩陣進行處理，而頻域分析法則是通過傅里葉變換、余弦變換、小波變換等變換方法將圖像從空域變換到頻域，在頻域的角度分析圖像的特征并進行處理。傅里葉變換是一種經典的圖像變換方法，本文基于傅里葉變換對散斑干涉相位圖在頻域上進行濾波去噪處理。

2.1 離散傅里葉變換

在計算機上，圖像的存儲采用數字形式，連續的傅里葉變換不適用于計算機的處理，因此在計算機圖像處理中的傅里葉變換一般都采用離散傅里葉變換(DFT)［16］。

對于圖像處理領域，由于圖像為二維矩陣數據，故采用二維離散傅里葉變換加以處理。其中，圖像尺寸為M×N函數的離散傅里葉變換及其反變換的公式為:

通常在進行傅里葉變換之前用(－1)x+y乘以輸入的圖像函數，可以將傅里葉變換的原點F(0，0)變換到頻率坐標下的(M/2，N/2)上。F(0，0)為圖像的平均灰度級，也被稱為頻域譜的直流分量。

2.2 頻域低通濾波

在傅里葉變換域，一幅圖像的能量大部分集中在其頻譜的低頻和中頻段，而圖像的邊緣和其他尖銳的跳躍(例如噪聲)則對傅里葉變換的高頻分量有很大貢獻。因此，對一幅圖像進行傅里葉變換得到頻譜后，對其頻域上一定范圍的高頻分量衰減，并使低頻分量順利通過，經過反變換可以達到圖像的平滑效果。

然而，由于相位圖存在跳變邊緣，跳變邊緣信息也屬于高頻分量，能否區分出噪聲與正常跳變將對濾波效果造成影響。

由卷積定理，頻域低通濾波的表達式為［17］:

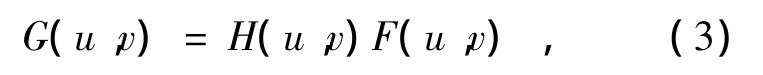
式中，F(u，v)為含有噪聲的原始圖像的傅里葉變換，H(u，v)為濾波器傳遞函數。常用的低通濾波器有理想低通濾波器、巴特沃斯濾波器、指數濾波器和梯形低通濾波器等。本文主要采用理想低通濾波器模型對圖像進行平滑處理。

一個二維理想低通濾波器的傳遞函數可以表示為:

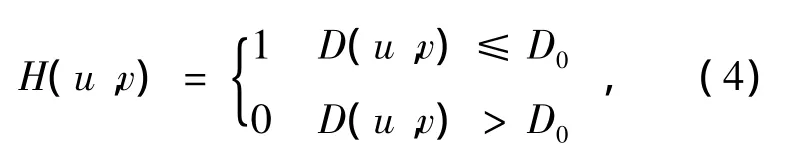
式中，D0為截止頻率。理想低通濾波器的特性為:假設傅里葉變換的原點已經處于N×N矩陣的中心，以D0為半徑的圓內的所有頻率分量無損通過，圓外的所有頻率分量完全衰減。

3 干涉相位圖的頻域去噪處理

圖3 頻譜及低通濾波結果Fig.3 Frequency domain and low-pass filter result

對實驗獲取的原始包裹相位(見圖1(a))進行二維傅里葉變換后得到的頻譜，如圖3(a)所示。根據上述原理，相位圖頻譜里的高頻分量對應著相位圖中的噪聲和條紋間的跳變信息，因此，如果直接對圖像進行頻域低通濾波，雖然濾除了原始相位圖中的噪聲，但是也嚴重損失了條紋圖中的跳變信息。圖3(b)為對圖3(a)直接進行傳統的頻域低通濾波得到的結果，可以看出產生一定的平滑效果，但同時也丟失了原始相位圖中的跳變信息。

為了保留原始相位圖中的“尖峰”信息，本文采取了一種基于正余弦變換的頻域低通濾波方法，得到了很好的平滑效果。該方法的基本思路是在對相位圖像進行頻域低通濾波處理前，先對將灰度分布呈鋸齒形函數分布的相位圖通過正余弦函數進行映射轉換成兩幅圖，分別經過頻域濾波，然后再合成為相位圖。這樣就可以在濾波的同時，有效保留相位跳變信息。映射轉換的規則如下式:

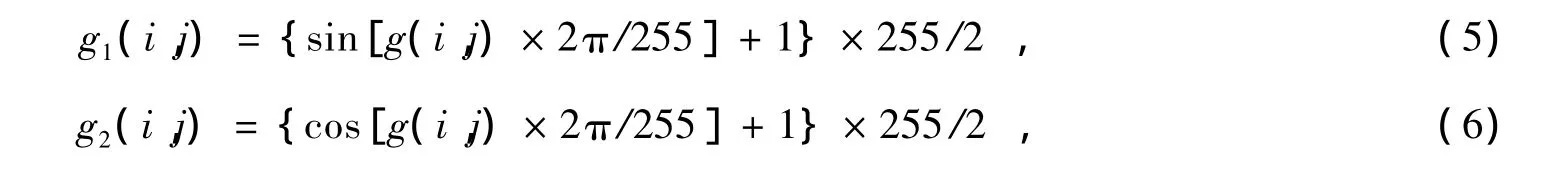
式中:g(i，j)為原始灰度值，g1(i，j)為轉換后的正弦灰度值，g2(i，j)為轉換后的余弦灰度值。

圖4 正余弦圖及處理效果Fig.4 Sine and Cosine fringe patterns and filter results

對圖1(a)進行轉換后的正弦圖和余弦圖如圖4(a)、4(b)所示。分別對其進行傅里葉變換，得到的頻譜如圖4(c)、4(d)所示。可以看出圖像的信息主要集中在頻譜的低頻部分，即圖像中心的亮斑。選用上節所介紹的二階理想低通濾波器對正弦圖和余弦圖進行頻域低通濾波，分別得到兩幅圖像的平滑結果，如圖4(e)、4(f)所示。

將濾波后得到的正余弦圖經過反運算合成一幅圖，就得到了最終的平滑結果，如圖5(a)所示。圖5(b)為其在x截面上的相位分布，從圖中可以看出，平滑效果比直接進行頻域低通濾波的效果更好，在圖中間和邊緣均取得了很好的濾波結果，圖像已經不再有任何散斑噪聲，并且很好地保留了條紋間的跳變信息。

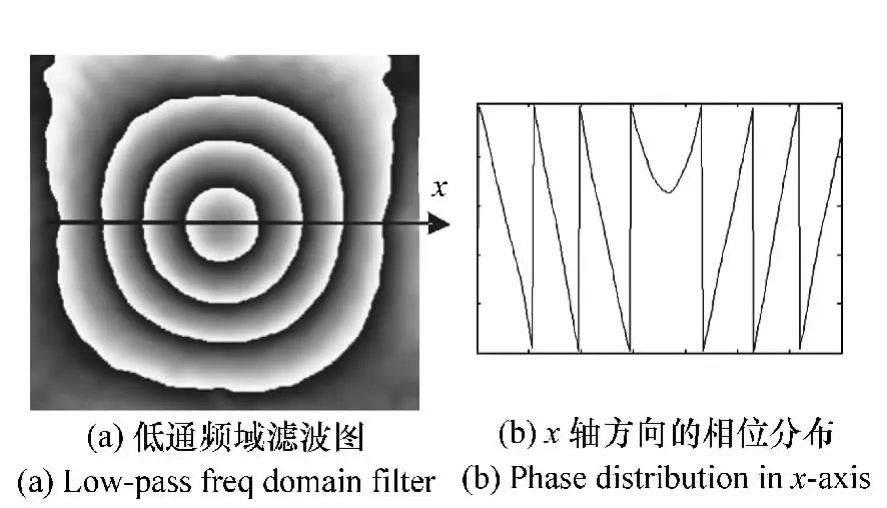
圖5 頻域濾波相位圖及相位分布Fig.5 Low-pass filtered phase map and phase distribution

圖6 解包裹相位對比圖Fig.6 Contrast of genuine phase map after unwrapping

圖6為對頻域濾波后的圖像進行相位解包得到的圖像，可見濾波后的相位圖進行解包裹處理獲得的結果也是很好的，證明了本文方法的有效性和可靠性。

4 測量實驗與結果

為研究頻域濾波方法對相位圖去噪的影響，本文分別對濾波次數、濾波窗口和截止頻率等參數的影響進行了實驗研究。頻域濾波的平滑效果可以通過增加濾波次數來實現，濾波次數越多，濾波結果越平滑。但是，濾波處理的時間也會成倍增加，影響了對相位信息提取的速度。圖7是采用3×3操作窗口進行空域濾波的實驗結果圖，a、b、c三幅圖的濾波次數分別為1次、3次和7次。

圖7 正余弦圖及處理效果Fig.7 Sine and Cosine filtered phase map with different filtering times

另一方面，空域濾波操作窗口的大小也會影響濾波結果的平滑程度，窗口越大，平滑效果越好。因此可以通過增大操作窗口來減少空域濾波的次數，但是相對濾波精度也會有所降低。圖8是采用不同操作窗口進行空域濾波的結果。

圖8 不同濾波窗口的空域濾波結果Fig.8 Filtered phase map with different size of operate window

選取不同大小截止頻率的二維理想低通濾波器，得到的濾波結果如圖9所示。比較后可以得出，頻域濾波后圖像的平滑程度與低通濾波器的截止頻率相關，截止頻率越小，濾波結果越平滑。因此只要選擇合適的截止頻率D0，一次濾波就可以得到理想的濾波效果，這樣相比于空域濾波，濾波的效率可以大大提高。

圖9 不同截止頻率下正余弦變換的頻域濾波結果Fig.9 Sine and Cosine filtered phase map with different cut-off frequency

通過濾波后相圖視覺效果及解包裹結果可以直觀地對濾波方法的優劣進行評判，而對濾波前后相位圖灰度信息保留比例的計算則可以客觀地展現不同方法的優劣。表1分別對原始相位圖以3種傳統方法與新方法在不同濾波窗口下進行一次濾波處理后的灰度保留比例做了對比。對于傳統濾波方法，加大濾波窗口對于灰度信息的丟失影響極大，在9×9窗口均值濾波中，損耗已經接近40%。對于相圖，由于灰度峰值基本出現在條紋跳躍處，故可以近似認為該處像素的濾波引入誤差接近40%。而新的分解頻域濾波方法中，灰度損耗僅為0.4%，且與濾波窗口大小無關，這樣就充分保護了相圖信息。

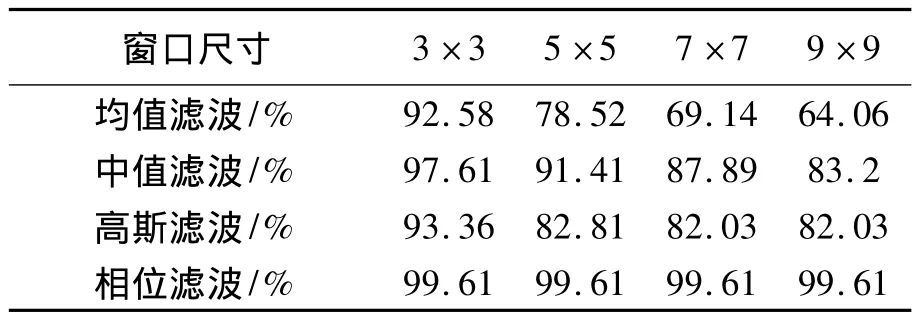
表1 灰度信息保留比例Tab.1 Retention rate of gray value after filtering

5 結論

干涉相位圖的降噪處理作為相位解包裹處理前的必要環節，如何在有效地去除條紋圖的散斑噪聲的同時，不會丟失和濾掉有用的信息(如相位跳變信息)是散斑干涉條紋處理的關鍵問題。本文采用相位圖正余弦映射分解和頻域濾波結合的方法，實現了散斑干涉條紋的高精度濾波，良好的平滑處理避免了噪聲對相位解包裹處理的干擾，使其可以順利的完成解包裹，最終得到正確的相位分布圖。實驗研究證明了該方法在較好地濾除圖像中散斑噪聲的基礎上，能夠有效保留相位中的“尖峰”信息，將傳統濾波方法中10% ～40%的灰度損耗降低至1%以下，能夠很好地滿足解包裹的需要，同時可以通過改變操作窗口大小、濾波次數和濾波器截止頻率等參數對不同程度的噪聲進行抑制，方法簡單有效。

［1］ 王開福.散斑計量學［M］.北京:北京理工大學出版社，2010.

WANG K F.Speckle Metrology［M］.Beijing:Beijing Institute of Technology Press，2010.(in Chinese)

［2］ GOODMAN G W.光學中的散斑現象-理論和應用［M］.北京:科學出版社，2010.GOODMAN G W.Speckle Phenomena in Optical［M］.Beijing:Science Press，2010.(in Chinese)

［3］ 王永紅，梁恒，王碩，等.數字散斑相關方法及應用進展［J］.中國光學，2013，6(4):470-480.

WANG Y H，LIANG H，WANG SH，et al..Advance in digital speckle correlation method and its applications［J］.Chinese Optics，2013，6(4):470-480.(in Chinese)

［4］ 孫志兵，陳麗.電子剪切散斑中的相位分析方法［J］.光子技術，2006，4(14):203-208.

SUN ZH B，CHEN L.Phase analysis method used in electronic speckle shearing interferometry［J］.Photonic Technology，2006，4(14):203-208.(in Chinese)

［5］ BURKE J，HELMERS H.Performance of spatial vs.temporal phase shifting in ESPI［J］.SPIE，1999，3744:188-199.

［6］ 金觀昌.計算機輔助光學測量［M］.2版.北京:清華大學出版社，2007.

JIN G CH.Computer-Aided Optical Metrology［M］.2rd edition.Beijing:Tsinghua University Press，2007.(in Chinese)

［7］ 宋凡峰.電子散斑相位檢測的濾波方法研究［J］.激光雜志，2007，28(3):50-51.

SONG F F.Investigation of filtering method for phase measurement in electronic speckle pattern interferometry(ESPI)［J］.Laser J.，2007，28(3):50-51.(in Chinese)

［8］ 高珊，馬艷會.基于邊緣保持的SAR圖像濾波算法研究［J］.液晶與顯示，2013，28(2):290-294.

GAO SH，MA Y H.Algorithm research of filtering for SAR images based on edges-preserving［J］.Chinese J.Liquid Crystals and Displays，2013，28(2):290-294.(in Chinese)

［9］ CAPANNI A，PEZZATI L，BERTANI D.Phase-shifting speckle interfereo-metry:a noise reduction filter for phase unwrapping［J］.Optical Engineering，1997，36(9):2466-2472.

［10］ AEBISCHER H A，STEPHAN W.A simple and effective method for filtering speckle-interferometric phase fringe patterns［J］.Opt.Commun.，1999，162(46):205-210.

［11］ QIN Y W，CHEN J L，FAN H B.The study and application of a new filtering method on electronic speckle pattern .interferometric fringe［J］.Optics and Lasers in Engineering，2003，39(4):449-456.

［12］ 楊磊，馮茜，王志剛，等.基于殘差點的干涉相位圖自適應濾波［J］.中國圖象圖形學報，2007，12(11):1976-1979.

YANG L，FENG Q，WANG ZH G，et al..Residues-based adaptive approach for phase image noise reduction［J］.J.Image and Graphics，2007，12(11):1976-1979.(in Chinese)

［13］ YU Q F，SUN X Y，LIU X L，et al..Span filtering with curve windows for interferometric fringe patterns［J］.Appl.Optics，2002，41(14):2650-2654.

［14］ 顧國慶，王開福.基于同態濾波的電子散斑干涉圖像處理［J］.激光技術，2010，34(6):750-797.

GU G Q，WANG K F.Electronic speckle interferometry image processing based on homomorphic filtering［J］.Laser Technology，2010，34(6):750-797.(in Chinese)

［15］ 李凱，張青川.基于Gabor濾波的散斑條紋圖平滑方法［J］.光學學報，2009，29(10):2751-2755.

LI K，ZHANG Q CH.Speckle fringe pattern smoothing method based on gabor filtering［J］.Acta Optica Sinica，2009，29(10):2751-2755.(in Chinese)

［16］ 丁玉美，高西全.數字信號處理［M］.西安:西安電子科技大學出版社，2007.

DING Y M，GAO X Q.Digital Signal Processing［M］.Xi'an:Xi'an University of Electronic Science and Technology Publishing House，2007.(in Chinese)

［17］ 岡薩雷斯.數字圖像處理［M］.3版.北京:電子工業出版社，2011.GONZALEZ.Digital Image Processing［M］.3rd edition.Beijing:Publishing House of Electronics Industry，2011.(in Chinese)