航空光電平臺機動目標跟蹤定位技術應用

劉 烜，胡倩影

（海軍裝備部航訂部，北京100841）

0 引言

隨著航空光電平臺的廣泛應用，利用航空光電平臺對機動目標進行實時偵察跟蹤定位，獲取目標位置及目標運動信息得到了各行業極大的關注。目前，在軍事領域利用航空光電平臺進行目標探測、目標指示等，在民用領域進行海面監控、海面搜救等方面。但是由于實飛過程中航空光電平臺和機動目標均處于運動狀態，且平臺運動速度遠遠大于機動目標的運動速度，對目標的跟蹤定位與航空光電平臺的姿態和動目標的運動狀態均有關，目標系統幾何校正精度存在一定的誤差，上述原因導致目標位置呈離散分布現象，無法正常解算目標的航向航速，所以在復雜的運動環境下實現對機動目標的跟蹤，提高目標定位及目標航向航速的精度就顯得尤為重要。為解決該問題，在計算目標航向航速前，利用卡爾曼濾波算法對目標位置進行濾波，提高對動目標的測量定位精度，均衡定位誤差，解決目標定位發散問題。并通過滑動加權方法進行目標航向解算，通過滑動平均方法進行目標航速解算，提高目標航向航速的精準度。最后通過實驗驗證本方法的可行性[1，2]。

1 目標位置濾波

卡爾曼濾波是以最小均方誤差作為估計的最佳準則，來尋求一套遞推估計的算法。其基本思想是:采用信號與噪聲的狀態空間模型，利用k時刻的估計值和k+1時刻的觀測值來更新對狀態變量的估計，求出k+1時刻的估計值[3，5]

1.1 系統建模

①系統矩陣

以機動目標的航跡點位置為例，系統矩陣可建立為四維矩陣，即經度、經度方向上的速度、緯度和緯度方向上的速度，它們分別用和表示，經度方向上的加速度和緯度方向上的加速度分別用ulon（k）和ulat（k）表示。

狀態方程為:

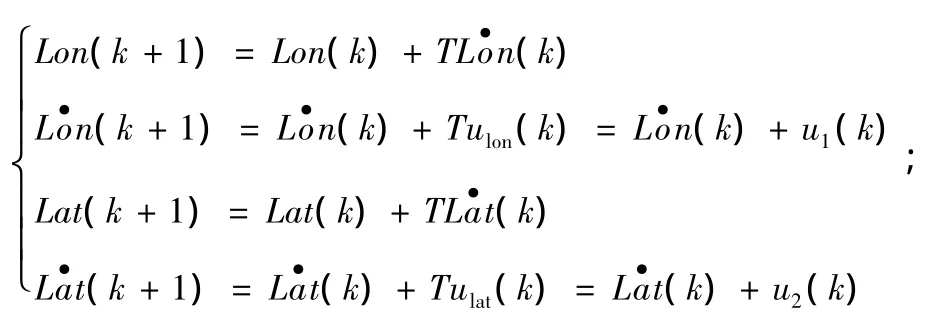
則系統方程為:

用標準符號x1、x2、x3和x4分別表示Lon和、Lat和。上式中，A為系統矩陣，W（k）為噪聲項，T為對目標的采樣周期。

②觀測矩陣

觀測值只有經度和緯度，即Lon和Lat，分別用z1和z2來表示。它們是由狀態值和測量噪聲組成的，且測量噪聲是相互獨立的零均值的白噪聲。

測量方程為:

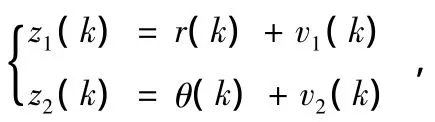
則觀測方程為:

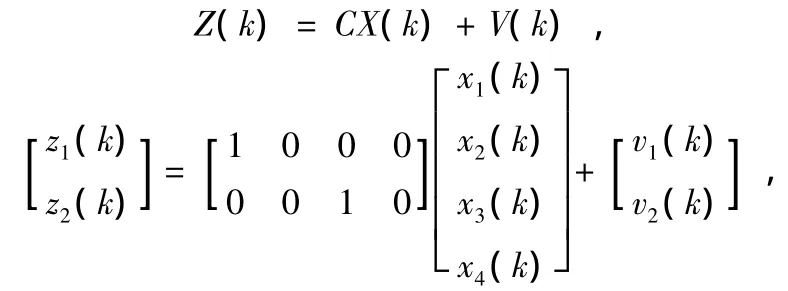
其中，x1（k）=r（k），x3（k）=θ（k）。

③系統噪聲協方差矩陣

假定機動目標從k時刻到k+1時刻做勻速運動，但由于大氣湍流等因素的影響，目標產生隨機加速度，在經度和緯度上都存在隨機擾動，于是有:

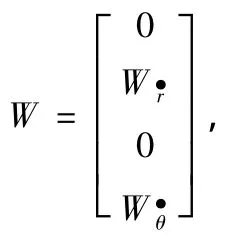
且

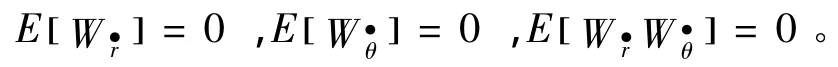
得輸入擾動的協方差矩陣:

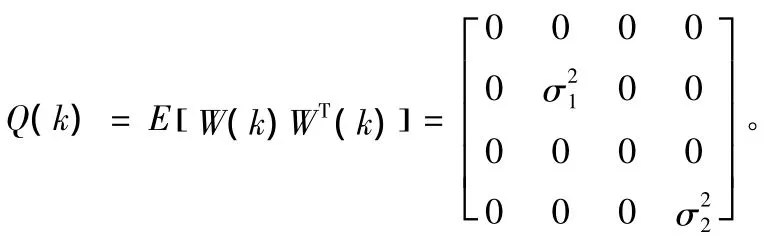
④觀測噪聲協方差矩陣

在計算濾波器增益時，需要知道觀測噪聲的協方差矩陣。由于只有兩個參數，因此:

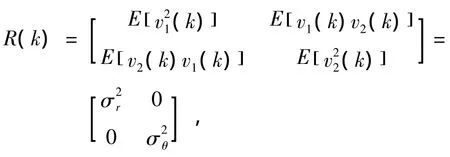
用了經度和緯度觀測噪聲相互獨立的條件，故左下角和右上角項為零。

⑤濾波器的初始值

在運算之前，必須對濾波器進行初始化。首先利用一種比較簡單的方法確定狀態估計值，可利用時刻1和時刻2兩點的經度和緯度測量值，即z1（1）、z1（2）、z2（1）和z2（2），建立，而忽略隨機加速度。

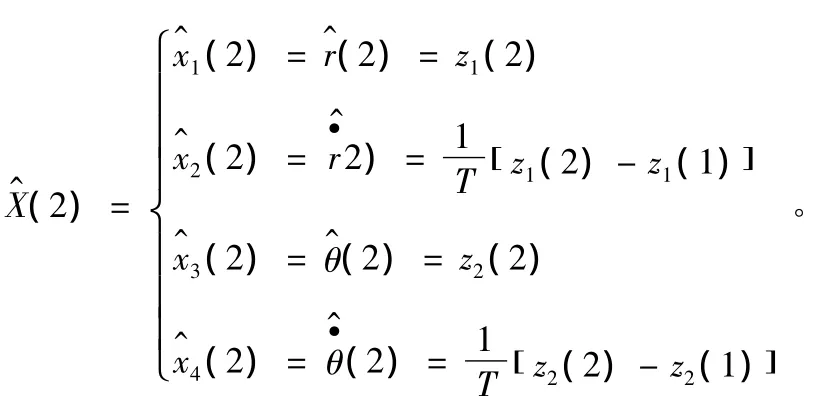
⑥均方誤差矩陣

由濾波器初值，有誤差矢量:

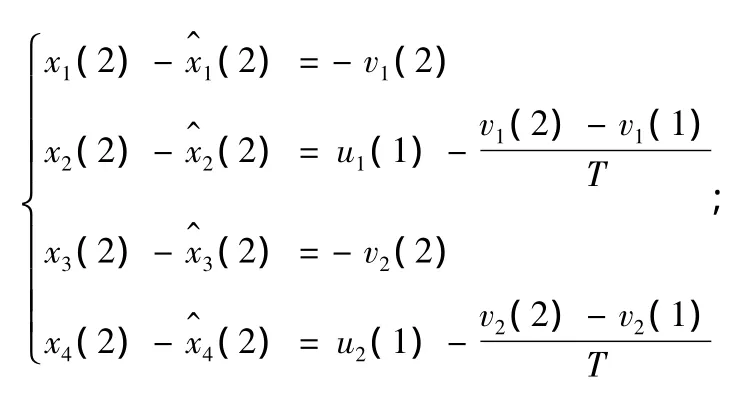
從而，

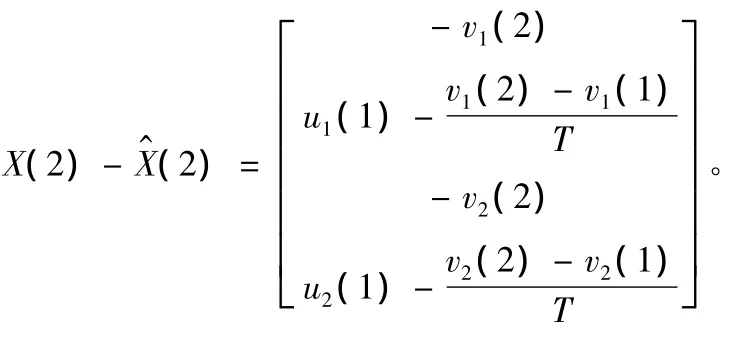
初始誤差的協方差矩陣:

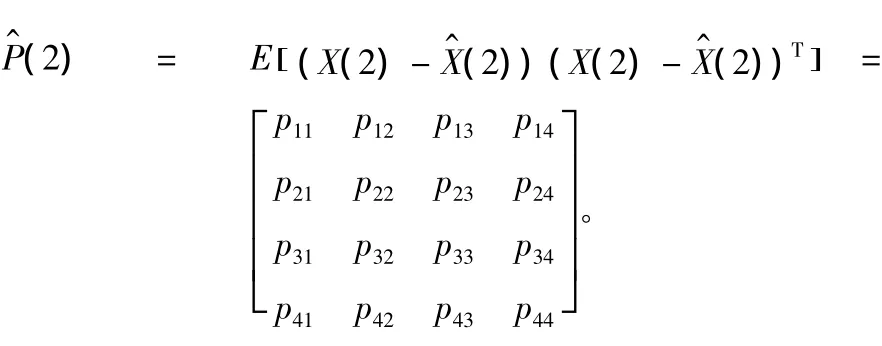
由于u和v相互獨立，且各噪聲采樣之間也獨立，則:

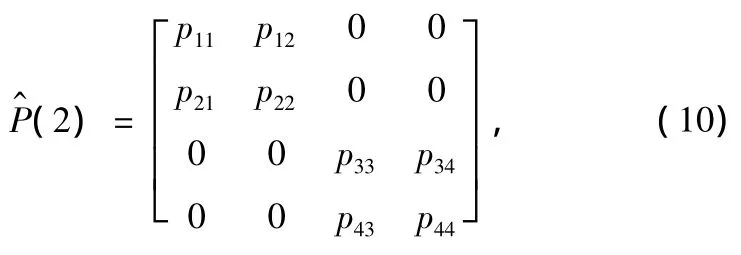
式中，

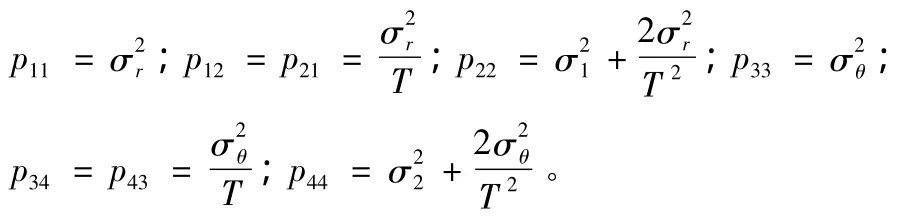
這樣，所需要的參數均已具備，可以進行迭代運算了。

1.2 卡爾曼濾波方程組

卡爾曼濾波算法采用遞推算法，計算步驟如下:

④由K（k+1）、Z（k+1）和，計算

其中，第③步和第④步計算順序可交換。

1.3 模型改進

該模型對于狀態值為連續的屬性項，濾波效果比較穩定。但是對于那些狀態值不連續的屬性項，比如機動目標航向角，當從360°（0°）連續變換到1°時，雖然對于目標的實際運動狀態來說是連續的，但對于濾波數據來說存在跳變，造成濾波效果不理想[6，7]。

為了解決該問題，將角度值進行了三角變換。記機動目標的航向角為θ，在直角坐標系中取單位圓上的點，則該點的橫坐標和縱坐標分別為x=rcosθ=cosθ，y=rsinθ=sinθ，x和y均為在[－1，1]區間連續變換的值。因此，對航向角θ的濾波計算轉換為對x和y的濾波計算。當計算出x和y的估計值和后，利用，可求得航向角的估計值。當然，該的范圍為[－90，90]，若要變換到[0，360]，可根據值和值的正負性，確定所在直角坐標系的象限，若為第一象限，則若為第二或第三象限，則若為第四象限，則

2 航向航速平滑解算

利用目標的大地位置坐標解算目標航向航速，目標的航向C和航速V的計算方法下面詳述[8，9]。

2.1 航向計算

通過上述計算方法獲取濾波后的目標坐標，由目標相鄰兩點坐標的連線方向確定目標航向，但由離散點坐標計算的目標航向呈不規則變化，跳動較大，不能真實地反映目標的航向，必須經過平滑處理才能進行分析計算。采用滑動加權方法進行航向平滑，取得較好的平滑效果。

滑動加權的具體方法是對于要計算的第n點的航向Cn，首先通過已知的第n點和第n－1點的位置坐標計算

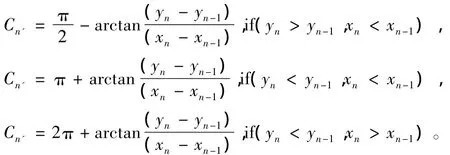
設定滑窗值為l，且已知n點前的l－1個點航向Ci+1，（i=0......l－2），滑窗內l個點對第n點的加權值分別為:，那么第n點的航向為:

2.2 航速計算

對于機動目標，一般來說其運動速度比航空光電平臺的運動速度小，為使目標航速逼近真實航速值，采用滑動平均的方法進行計算。具體方法是:假設目標在tk時刻的大地坐標為xk和yk，在tk+1時刻的大地坐標為xk+1和yk+1，設定滑窗值為l，對落入窗體內的l個動目標航跡點，從第1個開始，依次計算第k個與第k+1個值之間的距離，將窗體內的l－1個Vk值求和得，那么第n點的航速

3 定位精度分析

為了驗證本文濾波算法對目標定位精度的影響，以及驗證計算出的航向航速與真值的偏差，實驗在快艇上放置一套高精度GPS定位儀，用于記錄快艇的運動航跡及航向航速，通過航空光電平臺的遙測數據計算出的快艇位置及航向航速，將其與GPS獲取的位置及航向航速真值進行比對[5]。

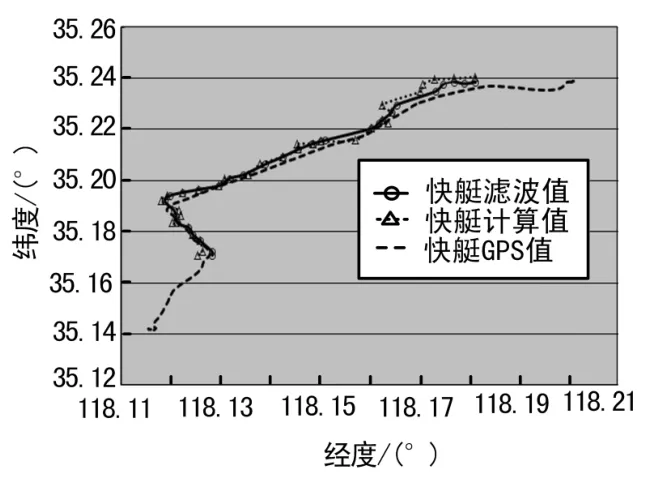
圖1 航空光電平臺動目標定位精度分析比對結果

其中:目標計算位置點坐標（x2，y2），GPS位置點坐標（x1，y1），按照經度方向1s距離約30m，緯度方向1s距離約27m進行計算，Δdi為測量值與真值間的偏差:

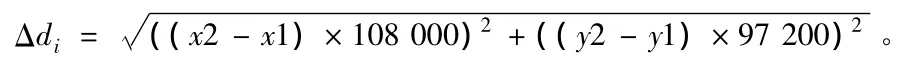
4 結束語

介紹了航空光電平臺動目標的跟蹤定位算法及在工程中的應用，以及動目標位置濾波算法及動目標航向滑動加權和航速滑動平均算法。在試驗中所用數據為光電平臺實時拍攝的視頻流及相應的平臺數據，機動目標搭載GPS定位數據，結果顯示目標位置更新頻率達到2次/s，濾波后目標定位誤差精度達到317.86m（均方根誤差），驗證了動目標位置濾波算法及動目標運動航向航速算法的可行性。

[1]高峰，馮碩，劉春華.高速幾何卡設計與實現[J].無線電工程，2010，40（5）:49－51.

[2]竇興川，王小東.基于DSP實現艦船目標檢測與跟蹤[J].無線電工程，2012，42（6）:32－34，38.

[3]李智生，余義德，杜寅峰，等.基于擴展卡爾曼濾波的水下目標測量系統[J].無線電工程，2011，41（4）:53－55.

[4]范洪達，李相民.卡爾曼濾波算法的幾何解釋[J].火力與指揮控制，2007，27（4）:48－50.

[5]俞卞章.數字信號處理[M].西安:西北工業大學出版社，2002:202－223.

[6]郭玲紅，李亞立.基于卡爾曼濾波的動目標運動參數跟蹤測量[J].自動化技術與應用，2012，31（8）:20－23.

[7]陳曦，殷華博.基于視覺運動目標跟蹤技術分析[J].無線電工程，2011，41（6）:22－24，39.

[8]梁民贊，黃子豪，曹占啟.曲線擬合與卡爾曼濾波器的濾波精度評估.無線電工程，2013，43（3）:36－39.

[9]李文靜.機動目標跟蹤算法[J].無線電工程，2012，42（1）:58－61.

[10]黃孟俊，陳建軍，趙宏鐘.海上目標航向航速解算新方法[J].信號處理，2011，27（7）:1034－1037.