基于專家經(jīng)驗(yàn)的振動(dòng)臺(tái)控制參數(shù)自整定方法研究1

紀(jì)金豹 孫麗娟 占鵬云 李 娜 張碩玉

（北京工業(yè)大學(xué) 工程抗震與結(jié)構(gòu)診治北京市重點(diǎn)實(shí)驗(yàn)室，北京 100124）

基于專家經(jīng)驗(yàn)的振動(dòng)臺(tái)控制參數(shù)自整定方法研究1

紀(jì)金豹 孫麗娟 占鵬云 李 娜 張碩玉

（北京工業(yè)大學(xué) 工程抗震與結(jié)構(gòu)診治北京市重點(diǎn)實(shí)驗(yàn)室，北京 100124）

地震模擬振動(dòng)臺(tái)控制系統(tǒng)的控制參數(shù)較多，其參數(shù)手動(dòng)整定費(fèi)時(shí)費(fèi)力，尤其對(duì)于多振動(dòng)臺(tái)臺(tái)陣系統(tǒng)，其手動(dòng)整定難度很大。基于上述問(wèn)題，根據(jù)專家進(jìn)行系統(tǒng)調(diào)試的經(jīng)驗(yàn)，提出了一種振動(dòng)臺(tái)控制參數(shù)自整定策略，分析了手動(dòng)整定中各參數(shù)對(duì)系統(tǒng)性能的影響，給出了自整定算法的整定規(guī)則，并通過(guò)Matlab仿真進(jìn)行振動(dòng)臺(tái)的控制參數(shù)自動(dòng)整定。通過(guò)比較自整定參數(shù)和理論計(jì)算參數(shù)下的時(shí)頻域特性，驗(yàn)證了本文所給出的自整定算法。結(jié)果表明，該方法具有簡(jiǎn)單實(shí)用及較好的實(shí)用價(jià)值，可供振動(dòng)臺(tái)參數(shù)自整定研究參考和借鑒。

地震模擬振動(dòng)臺(tái) 專家經(jīng)驗(yàn) 參數(shù)自整定

引言

地震模擬振動(dòng)臺(tái)是工程抗震領(lǐng)域主要的和可靠的試驗(yàn)設(shè)備之一。它在控制過(guò)程中面臨的最困難的問(wèn)題就是控制參數(shù)的整定問(wèn)題。振動(dòng)臺(tái)一般采用三參量控制算法，三參量控制參數(shù)的合理設(shè)置是振動(dòng)臺(tái)發(fā)揮控制性能的關(guān)鍵（Stoten等，2007）。合理的三參量控制參數(shù)組合可以拓寬系統(tǒng)有效的頻寬。反之，不但無(wú)法得到預(yù)想的控制效果，還有可能使振動(dòng)臺(tái)自激而損壞設(shè)備（范順成，2010）。振動(dòng)臺(tái)控制參數(shù)的整定主要有理論整定和經(jīng)驗(yàn)整定。其中，理論整定是基于被控對(duì)象的數(shù)學(xué)模型，通過(guò)理論推導(dǎo)計(jì)算得到控制器的控制參數(shù)；而經(jīng)驗(yàn)整定是專家通過(guò)實(shí)踐總結(jié)出來(lái)的調(diào)節(jié)參數(shù)的過(guò)程。楊志東（2009）采用根軌跡法描繪出振動(dòng)臺(tái)閉環(huán)系統(tǒng)極點(diǎn)與控制參數(shù)的數(shù)值關(guān)系，但實(shí)際系統(tǒng)模型與理論模型有較大差異，而且計(jì)算過(guò)程復(fù)雜繁瑣，得到的參數(shù)往往存在很大的誤差。韓俊偉（1997）利用實(shí)際頻率特性對(duì)振動(dòng)臺(tái)系統(tǒng)控制參數(shù)的匹配原理進(jìn)行了理論和試驗(yàn)研究，結(jié)果表明調(diào)節(jié)原則可保證振動(dòng)臺(tái)工作狀態(tài)最優(yōu)。但整定過(guò)程需要大量的反復(fù)調(diào)試，既耗時(shí)又費(fèi)力。對(duì)于某一特定控制系統(tǒng)，所整定的一組控制參數(shù)僅適用于某一工況，而實(shí)際工況總是隨著被控對(duì)象及環(huán)境因素等變化而改變。針對(duì)上述存在的問(wèn)題，筆者提出了一種基于專家經(jīng)驗(yàn)的參數(shù)自整定算法，該方法可快速得到最優(yōu)的三參量控制參數(shù)，使控制系統(tǒng)達(dá)到最優(yōu)。

1 地震模擬振動(dòng)臺(tái)系統(tǒng)分析

1.1 地震模擬振動(dòng)臺(tái)工作原理

地震模擬振動(dòng)臺(tái)的工作原理如圖1所示。地震波經(jīng)三參量發(fā)生器產(chǎn)生位移、速度和加速度三種信號(hào)，與通過(guò)傳感器采集的位移、加速度反饋信號(hào)，以及由兩種信號(hào)合成的速度反饋信號(hào)形成閉環(huán)控制系統(tǒng)，經(jīng)伺服閥將電信號(hào)轉(zhuǎn)換成液壓信號(hào)，從而驅(qū)動(dòng)液壓伺服缸，并推動(dòng)振動(dòng)臺(tái)臺(tái)面和模型試件按期望信號(hào)規(guī)律振動(dòng)（陳章位，2010）。

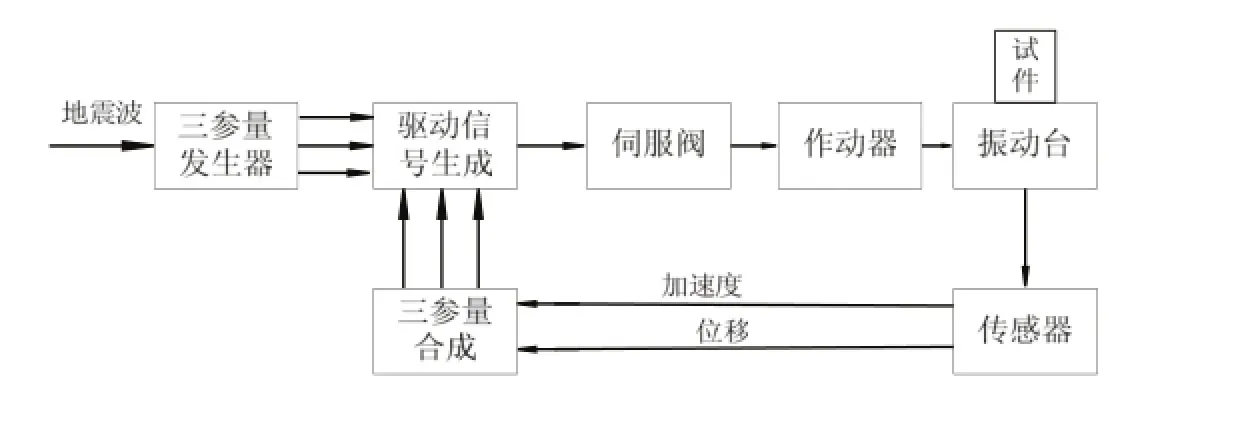
圖1 地震模擬振動(dòng)臺(tái)控制系統(tǒng)原理圖Fig. 1 Principle of shaking table control system

1.2 振動(dòng)臺(tái)系統(tǒng)模型

根據(jù)液壓控制理論，不考慮伺服閥動(dòng)態(tài)特性，振動(dòng)臺(tái)系統(tǒng)開(kāi)環(huán)傳遞函數(shù)如下：

式中，0n為液壓系統(tǒng)固有頻率；0D為液壓系統(tǒng)阻尼比；Kv為速度反饋增益；s為積分算子。

本文以北京工業(yè)大學(xué)工程結(jié)構(gòu)試驗(yàn)中心3m3m×的振動(dòng)臺(tái)為研究對(duì)象，其性能指標(biāo)如表1所示。

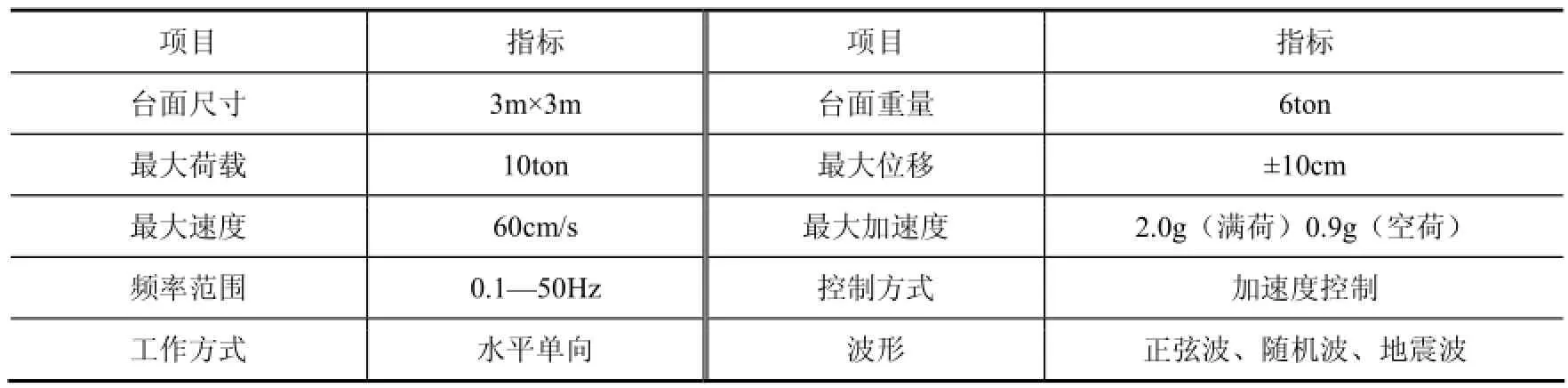
表1 地震模擬振動(dòng)臺(tái)系統(tǒng)性能指標(biāo)Table 1 The parameters of the shaking table

1.3 三參量控制原理

三參量控制器是地震模擬振動(dòng)臺(tái)控制系統(tǒng)的重要組成部分。三參量控制算法主要是為了補(bǔ)償?shù)卣鹉M振動(dòng)臺(tái)僅有位移控制時(shí)頻寬小、阻尼小的缺陷，從而更好地實(shí)現(xiàn)不同頻段的加速度、速度、位移控制。三參量控制中采用位移控制低頻段，速度控制中頻段，加速度控制高頻段，從而實(shí)現(xiàn)增大系統(tǒng)阻尼，拓寬系統(tǒng)頻帶的目的（李振寶，2010）。

控制器主要由三參量反饋控制器和前饋控制器組成。其中，三參量反饋控制器的作用是通過(guò)調(diào)節(jié)afk、vfk和dfk三個(gè)反饋系數(shù)提高系統(tǒng)阻尼比和共振頻率，擴(kuò)寬系統(tǒng)頻率適用范圍，增強(qiáng)系統(tǒng)穩(wěn)定性；而三參量前饋控制器的作用是通過(guò)調(diào)節(jié)ark、vrk和drk三個(gè)前饋參數(shù)抵消系統(tǒng)閉環(huán)傳遞函數(shù)中距離虛軸較近的極點(diǎn)，進(jìn)一步拓展系統(tǒng)的工作頻寬（于浩洋，2013）。三參量控制原理如圖2所示，圖中0d、0v為濾波器的兩參數(shù)，VelSyn為速度合成器模塊。

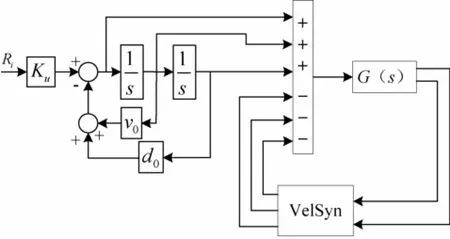
圖2 三參量控制原理圖Fig. 2 Schematic diagram of three-parametric control

2 專家經(jīng)驗(yàn)參數(shù)自整定方法的原理

基于專家經(jīng)驗(yàn)的參數(shù)自整定方法是總結(jié)專家的參數(shù)整定經(jīng)驗(yàn)，模擬專家手動(dòng)整定的過(guò)程，利用一系列的整定規(guī)則表示專家知識(shí)，使參數(shù)快速、精確地達(dá)到最優(yōu)值，有效解決地震模擬振動(dòng)臺(tái)手動(dòng)調(diào)整參數(shù)耗時(shí)存在的一些關(guān)鍵問(wèn)題。以下是根據(jù)手動(dòng)調(diào)整臺(tái)的經(jīng)驗(yàn)給出的調(diào)整規(guī)則（黃浩華，2008）。

（1）調(diào)節(jié)位移反饋增益dA′和位移前饋增益dA

由于振動(dòng)臺(tái)采用加速度控制方式，在開(kāi)環(huán)情況下系統(tǒng)無(wú)法定位，因此引入位移反饋形成閉環(huán)控制系統(tǒng)，可使系統(tǒng)受控。調(diào)節(jié)增益使加速度前饋aA、速度前饋vA、加速度反饋aA′、速度反饋vA′均為0，逐步調(diào)節(jié)位移增益。如圖3所示，系統(tǒng)的頻帶寬度隨著增益的增大而變寬，且能夠明顯地看到油柱共振峰，其對(duì)應(yīng)的頻率即為油柱共振頻率。

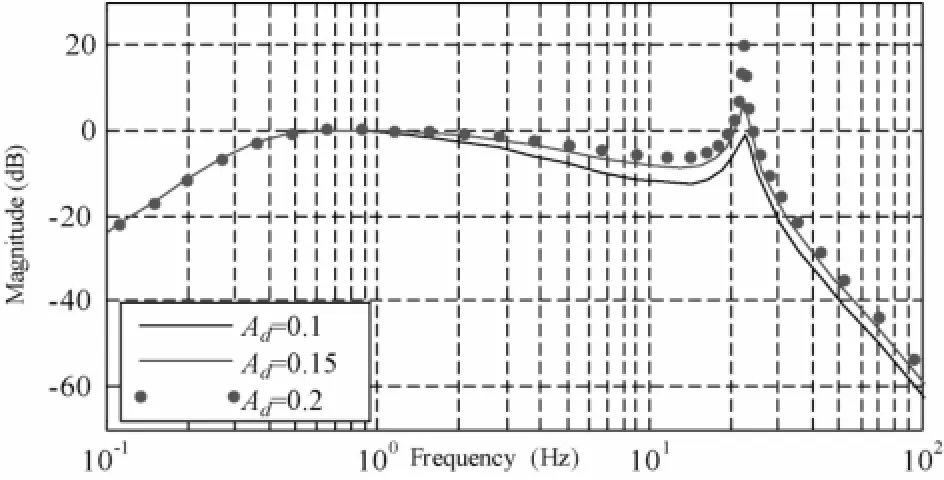
圖3 僅存在位移反饋時(shí)的系統(tǒng)頻響特性曲線Fig. 3 Frequency-response curve under displacement feedback

根據(jù)手動(dòng)調(diào)整臺(tái)的經(jīng)驗(yàn)，調(diào)節(jié)位移增益一般使平坦部分約在5Hz左右，取圖3中0.5—5Hz之間所有點(diǎn)幅值絕對(duì)值的平均值小于一個(gè)較小的值1ε，使得在此區(qū)間范圍內(nèi)的頻響曲線盡可能平坦。按式（2）原則對(duì)位移增益進(jìn)行調(diào)整：

（2）調(diào)節(jié)加速度反饋增益Aa′

調(diào)節(jié)加速度反饋參數(shù)可以增大系統(tǒng)的阻尼比，削平油柱共振峰。如圖4（a）所示可以看出，逐級(jí)增加加速度反饋控制量，油柱共振峰逐漸減小。算法中取油柱共振頻率n0左邊的上限值頻率n0?ω1和右邊的下限值n0+ω2頻率之間幅值的平均值小于頻率n0?ω3處的幅值，如圖4（b）所示。按式（3）原則對(duì)加速度反饋增益進(jìn)行調(diào)整：

式中，A(n0?ω1～n0+ω2)為頻響圖中頻率n0?ω1到n0+ω2之間幅值的平均值；A(n0?ω3)為頻率n0?ω3點(diǎn)的幅值。

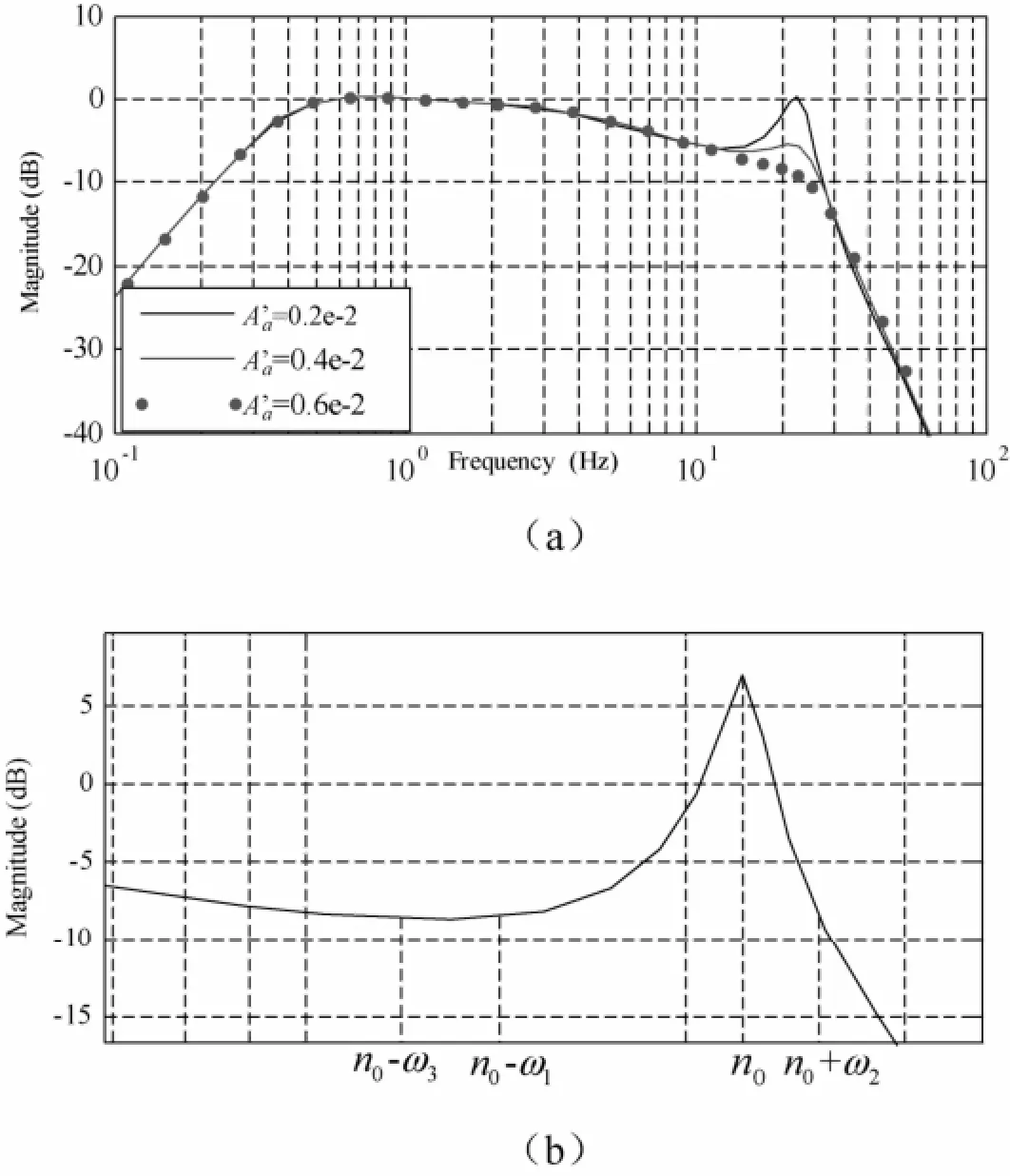
圖4 加速度反饋下頻響特性曲線Fig. 4 Frequency-response curve under acceleration feedback

（3）調(diào)節(jié)速度前饋增益vA

速度前饋增益可以調(diào)節(jié)系統(tǒng)的中頻段頻寬。如圖5所示，隨著增益值的增大，中頻段更為平坦，取頻響圖中5—10Hz之間所有點(diǎn)幅值絕對(duì)值的平均值小于一個(gè)較小的值2ε，使得在此區(qū)間范圍內(nèi)的曲線盡可能的平坦。由此給出速度前饋增益的調(diào)整規(guī)則：

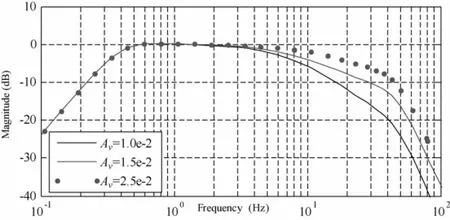
圖5 調(diào)節(jié)速度前饋下頻響特性曲線Fig. 5 Frequency-response curve under speed feedforward

（4）調(diào)節(jié)加速度前饋增益aA

調(diào)節(jié)加速度前饋增益可以擴(kuò)展系統(tǒng)的高頻段頻寬。如圖6所示，系統(tǒng)頻響特性曲線中的高頻部分隨著加速度前饋增益的增加呈上升的趨勢(shì)。取頻響圖中5—10Hz之間所有點(diǎn)幅值絕對(duì)值的平均值小于一個(gè)較小的值3ε，使得在此范圍區(qū)間頻響曲線盡可能接近0dB。由此給出加速度前饋增益的調(diào)整規(guī)則：式中，表示頻響圖（圖6）中，10—45Hz之間幅值絕對(duì)值的平均值。

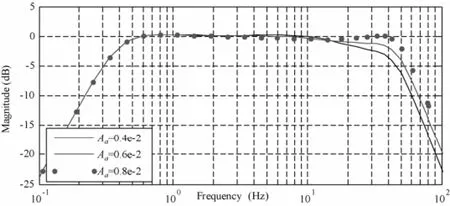
圖6 調(diào)節(jié)加速度前饋下頻響特性曲線Fig. 6 Frequency-response curve under acceleration feedforward

（5）如果頻寬未達(dá)到要求，可調(diào)節(jié)速度負(fù)反饋，且應(yīng)同時(shí)調(diào)節(jié)加速度負(fù)反饋，可達(dá)到提高油柱共振頻率的目的，且仍可保證不出現(xiàn)油柱共振峰點(diǎn)。然后調(diào)節(jié)速度和加速度前饋，可進(jìn)一步拓寬頻帶。

3 參數(shù)自整定算法仿真與對(duì)比驗(yàn)證

3.1 參數(shù)自整定算法仿真

由以上算法可得到如圖7所示的地震模擬振動(dòng)臺(tái)控制參數(shù)自整定流程圖。圖7中h1、h2、h3、h4和h5分別為位移增益、加速度反饋增益、速度前饋增益、加速度前饋增益和速度反饋增益的步長(zhǎng)，δ1、δ2為較小的固定值，其他參數(shù)與前文意義一致。自整定過(guò)程的輸入信號(hào)采用白噪聲序列，噪聲幅值為0.05g，信號(hào)采樣時(shí)間0.002s，振動(dòng)臺(tái)自身的參數(shù)取值如表2所示。

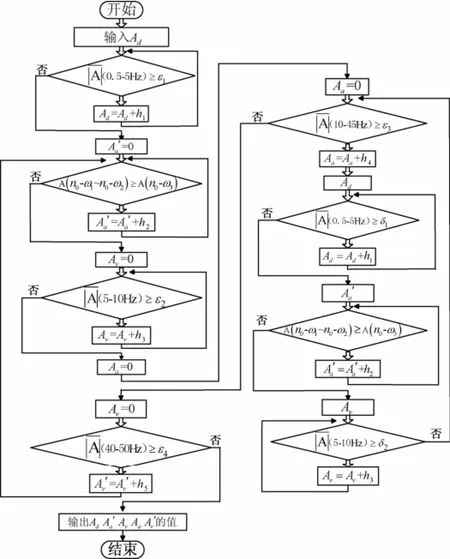
圖7 自整定算法流程圖Fig. 7 Flow diagram of auto-tuning algorithm

表2 地震模擬振動(dòng)臺(tái)仿真參數(shù)Table 2 The simulation parameters of shaking table

由振動(dòng)臺(tái)的輸入、輸出數(shù)據(jù)可得到系統(tǒng)的頻響特性，依據(jù)建立的規(guī)則自動(dòng)調(diào)節(jié)控制參數(shù)。由上述建立的振動(dòng)臺(tái)模型，并考慮伺服閥為二階振蕩環(huán)節(jié)，伺服閥傳遞函數(shù)如式（7）所示。采用自行編制的自整定程序得到的自整定參數(shù)值和采用黃浩華（2008）給出的控制參數(shù)計(jì)算公式得到的參數(shù)值如表3所示。

式中，qn為伺服閥二階系統(tǒng)固有頻率；qD為伺服閥二階系統(tǒng)阻尼比；s為積分算子。

表3 三參量控制器控制參數(shù)值Table 3 Control parameters of TVC

3.2 參數(shù)自整定算法對(duì)比驗(yàn)證

由表2可以看出，自整定值與理論值存在一定的差異，但其控制效果需通過(guò)時(shí)頻曲線對(duì)比才能下結(jié)論。以El-centro地震波為例進(jìn)行系統(tǒng)仿真，對(duì)基于專家經(jīng)驗(yàn)的自整定算法控制效果與理論計(jì)算參數(shù)的整定效果進(jìn)行比較，響應(yīng)曲線如圖8所示。由圖8（a）可以看出，系統(tǒng)頻響曲線在0.5—50Hz范圍內(nèi)較為平坦，基本保持在±3dB范圍內(nèi)；由圖8（b）可以看出，輸出信號(hào)時(shí)程曲線吻合較好，信號(hào)之間的相關(guān)系數(shù)可達(dá)到0.932，即在工作頻寬內(nèi)輸出信號(hào)能較好地復(fù)現(xiàn)輸入控制信號(hào)。這些都表明，利用基于專家經(jīng)驗(yàn)的控制參數(shù)自整定算法可以得到較好的控制參數(shù)。

4 結(jié)論

本文結(jié)合地震模擬振動(dòng)臺(tái)系統(tǒng)手動(dòng)整定參數(shù)的經(jīng)驗(yàn)，提出了一種基于專家經(jīng)驗(yàn)的自整定算法。分析了手動(dòng)整定過(guò)程中各參數(shù)對(duì)系統(tǒng)性能的影響，以頻率響應(yīng)曲線作為控制器參數(shù)自整定的依據(jù)，明確了自整定算法的設(shè)計(jì)步驟。通過(guò)Matlab進(jìn)行的仿真研究表明，此算法簡(jiǎn)單、有效，且容易被技術(shù)人員理解掌握，具有較好的實(shí)用價(jià)值。

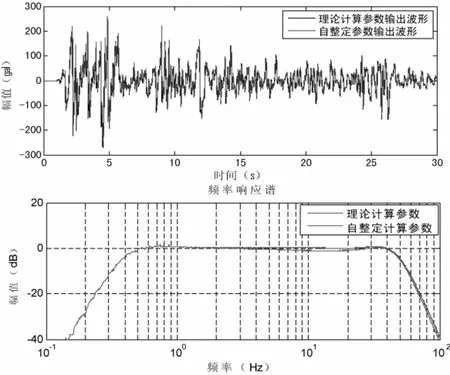
圖8 自整定參數(shù)下系統(tǒng)仿真結(jié)果對(duì)比曲線Fig. 8 The system simulation correlation curve with the Auto-tuning parameters

陳章位，2010. 液壓振動(dòng)臺(tái)控制策略的研究．汽車零部件，（8）：79—82．

范順成，2010．地震模擬振動(dòng)臺(tái)狀態(tài)控制參數(shù)配置的研究．天津：Scientific Research Publishing．USA．

黃浩華，2008．地震模擬振動(dòng)臺(tái)的設(shè)計(jì)與應(yīng)用技術(shù)．北京：地震出版社，57—76．

韓俊偉，1997．地震模擬振動(dòng)臺(tái)初始狀態(tài)調(diào)節(jié)和控制參數(shù)的匹配．地震工程與工程振動(dòng)，（1）：116—121．

李振寶，2010．地震模擬振動(dòng)臺(tái)三參量控制算法超調(diào)修正．振動(dòng)與沖擊，10（29）：211—215．

楊志東，2009．液壓振動(dòng)臺(tái)振動(dòng)環(huán)境模擬的控制技術(shù)研究．哈爾濱：哈爾濱工業(yè)大學(xué)．

于浩洋，2013．電液振動(dòng)臺(tái)加速度波形再現(xiàn)控制算法．黑龍江工程學(xué)院學(xué)報(bào)（自然科學(xué)版），227（1）：60—63．

Stoten D.P.，Shimizu N.，2007．The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables．Proceedings of the Institution of Mechanical Engineers，Part I． Journal of Systems and Control Engineering，221（3）：423—444．

Control Parameters Auto-Tuning Methods of Shaking Table Based on Expert Experiences

Ji Jinbao，Sun Lijuan，Zhan Pengyun，Li Na and Zhang Shuoyu

（Beijing Laboratory of Earthquake Engineering and Structural Retrofit，Beijing University of Technology，Beijing 100124，China）

The parameter setting manually for the control system is time-consuming，especially for many vibration tables．Based on the experience of expert system for debugging a vibration table control parameter self-tuning strategy，we proposed a method to control parameters setting automatically through Matlab for shaking table．It is proved that our algorithm is correct by setting parameters and theoretical calculation of the time and frequency domain properties．

Shaking table；Specialist experiences；Parameters auto-tuning

紀(jì)金豹，孫麗娟，占鵬云，李娜，張碩玉，2014．基于專家經(jīng)驗(yàn)的振動(dòng)臺(tái)控制參數(shù)自整定方法研究．震災(zāi)防御技術(shù)，9（4）：882

．

10.11899/zzfy20140416

1 ［基金項(xiàng)目］ 國(guó)家自然科技基金資助項(xiàng)目（51278013，51108428）

2014-04-14

紀(jì)金豹，男，生于1974年。高級(jí)實(shí)驗(yàn)師。主要從事結(jié)構(gòu)振動(dòng)控制、結(jié)構(gòu)試驗(yàn)技術(shù)方面的研究工作。E-mail：jinbao@bjut.edu.cn