基于Logit模型的商業銀行個人貸款業務風險成因實證研究

●張婧

基于Logit模型的商業銀行個人貸款業務風險成因實證研究

●張婧

文章運用logit模型對我國商業銀行個人貸款業務風險成因進行了實證研究，發現受教育程度與經濟狀況對個人貸款違約率有顯著影響，商業銀行在發放個人貸款業務前除了考察年齡、婚姻狀況等因素外，應重點考察這兩個因素。

個人貸款 logit 模型 風險成因

一、引言

改革開放以來，中國經濟得到了快速發展，尤其是金融市場的逐步放開，使得金融業逐漸成長為現代經濟的核心部分。隨著居民收入的不斷提高，消費觀念及水平的不斷變化，個人對信用消費的需求逐漸增加，再加上房地產業一直是國民經濟重要的增長點。商業銀行個人貸款業務，如個人住房按揭等得到快速發展。在銀行業大量進行重組、兼并、股份制化等改革后，保障銀行業的健康運行十分必要。然而我國金融市場上的融資行為主要還是依靠銀行間接融資，以證券、債券等為主的直接融資方式還很不成熟，這就導致銀行成為了風險聚集處。眾所周知，商業銀行主要的利潤來源是存貸款利差，主要業務是吸收存款和發放貸款，因此，商業銀行面臨的主要風險是貸款風險管理①。

在我國，隨著個人貸款業務市場的不斷擴大，許多商業銀行都表現出個人貸款業務粗放型風險管理與業務快速發展不匹配的現象，一些商業銀行的個人貸款業務風險管理體系已不能適應個人貸款業務風險防控管理的要求②③④。對商業銀行而言，個人貸款業務見效快、增長明顯。比如，2009年個人貸款增長率為40.01%，較企業貸款21.56%的增長率而言增長速度更顯著，但個人貸款業務風險的累積速度和程度也是極高的，因此能否很好地防范和化解個人貸款業務風險不僅關系到商業銀行的業績表現，更與其長遠發展有著不可忽視的聯系。因此商業銀行必須對現行的個人貸款業務風險管理體系進行有效地改進與完善，使之與蓬勃發展的個人信貸業務水平相匹配，以保持個人信貸業務穩健發展。

二、模型的選擇及變量的選取

1.模型的選擇。在本文所研究的問題中，個人貸款是否違約就是一種決策變量，由于需要研究個人特征如何影響個人貸款違約發生，所以選擇logit模型來模擬決策的發生。

對商業銀行個人貸款違約的風險進行模擬，該模型中因變量是二值變量，代表個人貸款違約是否發生，如果發生違約，則因變量取值為1；反之，因變量取值為0。解釋變量是個人特征變量，如個人受教育程度、經濟狀況、年齡和婚姻狀況等。我們在取得樣本數據后，運用SPSS統計軟件，將樣本數據帶入建立的logit線性回歸方程，得出解釋變量對于被解釋變量即個人特征變量對于個人貸款違約與否的影響與關系，評估出個人貸款違約的主要影響因素，從而達到對商業銀行個人貸款業務風險的主要影響因素進行判別的目的⑤。

Logit分布函數的表達式為：

設Zi=β1+β2Xi時，上式可寫為：

記Pi為事件發生的概率，則Pi不發生的概率為,

機會比率的定義為事件“發生”與“沒有發生”的概率之比

將（2）和（3）代入得到

對上式兩邊取自然對數：

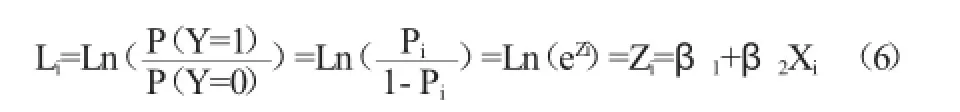
此模型稱為對數單位模型（logit模型），可見Xi變動一個單位，機會比率的對數平均變化β2個單位。

為對數單位，這里的對數單位Li是對Xi和β的線性函數。

2.Logit模型的參數估計方法——極大似然估計。在線性回歸中估計總體未知參數時，為使被解釋變量的觀測值與模型估計值之間的參差平方值為最小，通常采用最小二乘法的方法。最大似然估計方法在線性回歸分析中，可以得到與最小二乘法一致的結果⑥⑦。但與最小二乘法相比，最大似然估計法既可以用于線性模型，又可以用于非線性模型，由于logit回歸模型是非線性模型，因此選擇最大似然估計法對logit回歸模型進行估計⑦。

接下來我們以單變量為例，說明極大似然估計方法的原理。

設被估計的模型如下：

如果第一種選擇發生了n次，則第二種選擇發生了N-n次。設第一種選擇的概率是Pi，第二種選擇的概率是1-Pi。則n次觀察的似然函數為：

最大似然估計就是求解出能夠最大化似然函數的參數值和。上式也可表示為：

兩端取對數：

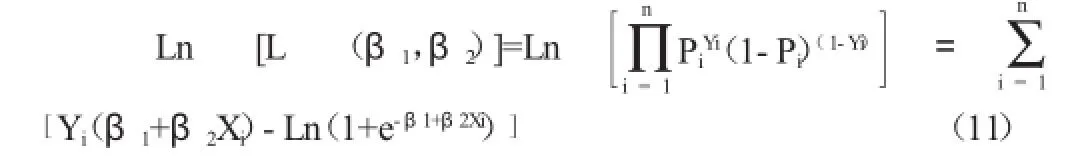
為了求出能夠使得似然函數最大化的參數，分別對和求偏導數，并令其為0，得

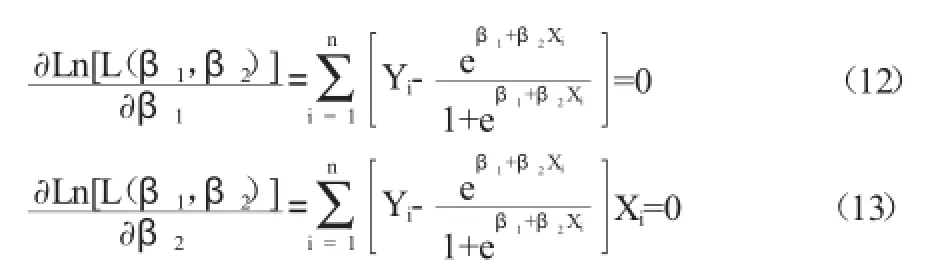
本文的風險評估模型中Logit分布函數是多變量函數，所以我們需講原模型進行轉化，假設Z為影響違約概率的因素的線性組合，即：a0+a1y1+a2y2+…amym，則p=1/（1+e-（a0+a1y1+a2y2+…amym）），通過取對數將其轉變成線性函數，得：Logitp=Ln（pi/（1-pi）），

其中，p是個人貸款發生違約的可能性，即違約概率，y1，y2，…，ym是個人特征變量，是待估計參數。

3.變量的選取。

（1）解釋變量的選取。影響個人貸款違約的特征因素非常多。本文選取受教育程度（用y1表示）、經濟狀況（用y2表示）、年齡（用y3表示）和婚姻狀況（用y4表示）作為模型的解釋變量。

對于受教育程度。通常受教育程度越高，信用狀況越好，貸款違約的可能性越低。本文將受教育程度分為5個等級。依次為：文盲、小學、初中（含技工學校）、高中（含中專）、大學及以上，依次賦值為1、2、3、4、5。

對于經濟狀況，一般來講，固定資產和年收入越高，貸款違約的概率越低。經濟狀況主要包括年收入水平和固定資產價值，這是一個量化指標，可以直接用原有的數據加總。

對于年齡，年輕人相對于中年人貸款違約的現象多。年齡主要劃分為4個等級18～30歲、30～40歲、40～50歲、50歲以上（考慮到法律責任的問題以及現實情況中的限制條件，18歲以下的年齡不予考慮），分別賦值為1、2、3、4。

最后是婚姻狀況，單身的人承擔風險的能力可能不足與一個家庭相比，因此，本文在這里也選取婚姻狀況作為衡量貸款違約狀況的一個指標。假定未婚為1，已婚為2。

（2）被解釋變量的測量：關于“違約”的界定。目前，許多商業銀行信貸管理采用了國際通用的“五級分類法”，該方法分為五個等級即“正常、關注、次級、可疑和損失”，后三者稱為“不良貸款”⑧。本文根據“五級分類法”對貸款進行分類，次級以上貸款定為高風險客戶（用1表示），其他貸款為低風險客戶（用0表示）。

三、基于Logit模型的商業銀行個人貸款業務風險成因實證研究

本文使用的數據來自某商業銀行數據庫中相關個人貸款數據資料，我們利用該數據庫使用logit模型來分析個人特征對于個人貸款違約概率的影響。

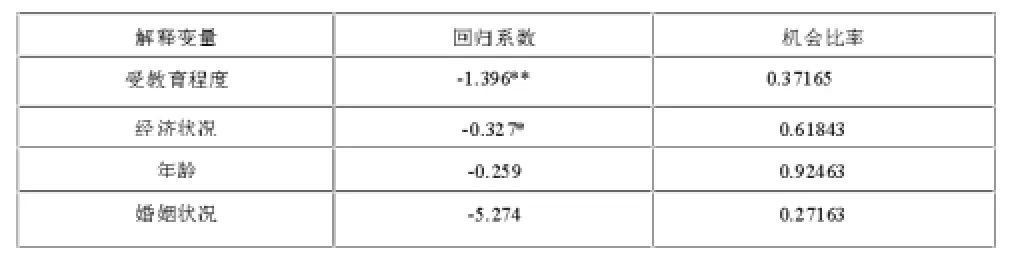
表1 Logit模型回歸結果

為了得到有代表性的數據，我們首先對原始數據進行加工。樣本選擇必須覆蓋全部指標，對于某項指標數值缺失的記錄，直接剔除該記錄。最后得到一個容量500的新樣本。500個樣本分為訓練組（350個）和預測組（150個）。依照“五級分類法“，定義的高風險客戶和低風險客戶標準。訓練組高風險客戶89戶，低風險客戶261戶。預測組中高風險客戶33戶，低風險客戶117戶。

然后將各變量值代入公式（16），經過SPSS計算得出

則

由表1可以看出，四個解釋變量中受教育程度與經濟狀況分別在5%與10%的顯著水平下顯著，這意味受教育程度和經濟狀況對個人信用貸款的違約風險具有顯著的影響。年齡和婚姻狀況兩個解釋變量：雖然不統計顯著，但其參數符號和機會比率符合我們的預期，對他們的解釋有一定的經濟學意義。受教育程度的顯著水平為5%，說明該因素對個人信用風險有著顯著影響，其系數為-1.396，機會比率為0.37165。這意味著受教育程度越高,違約風險越低。這一結論與之前的預測相符合。經濟狀況，其系數為-0.327，機會比率為0.61843。說明隨著經濟狀況的提升違約風險呈降低趨勢。年齡與婚姻狀況這兩個因素在統計上不顯著，其系數分別為-0.259,-5.274,機會比率分別為0.92463和0.27163。這表示年齡大的人的違約風險小于年輕人，已婚人士的違約風險遠小于未婚人士。由此模型可以得出結論：教育水平的提高、經濟狀況的提升個人違約風險降低；年長人士及已婚人士的違約風險小于未婚人士。從回歸方程中可以得知，受教育程度、經濟狀況、年齡和婚姻狀況等方面對個人是否違約的作用較大。

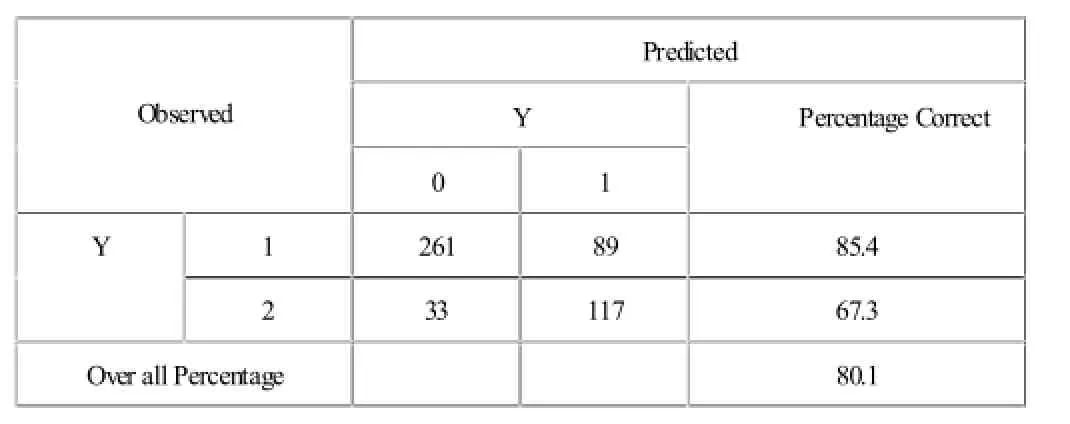
表2 模型預測結果表

基于極大似然估計方法對貸款風險進行評估，從表2易知，訓練組和預測組的判別正確率分別為85.4%和67.3%，最終模型正確率80.1%。從結果可以看出，此模型具有較強的實用性，對商業銀行的個人貸款信用風險評估有較好的指導意義。

四、研究結論

本文構造了我國商業銀行個人貸款風險的logit模型，并選擇某商業銀行500個客戶的信息和數據作為檢測樣本，通過構建的模型進行實證分析，計算出不同等級個人違約概率，并且進行信用風險判別和比較研究。通過分析論證得出以下結論：

1.商業銀行在個人貸款風險管理中，應充分重視信用風險度量模型和評級方法的使用。本文建立的違約概率logit預測模型，很大程度上證明了對預測商業銀行個人貸款風險評估中個人違約概率的有效性。

2.對我國商業銀行獲取的客戶個人信息和數據，利用所構建的違約概率logit預測模型，可以幫助商業銀行對貸款人的信用風險進行判定，從而為降低不良貸款率提供可信任的客觀依據。

3.個人特征信息，特別是受教育程度及經濟狀況等對貸款違約情況有顯著影響，故商業銀行在發放個人貸款前應重點考察這兩個因素。

注釋：

①柴建新.商業銀行貸款項目風險評價研究[D].華北電力大學,2008

②黃學軍.商業銀行個人貸款業務風險管理研究[D].湖南大學,2008

③鄭超.基于項目管理的商業銀行并購貸款風險管理[J].現代管理科學,2012(1)

④將亞利.中國商業銀行個人金融業務操作風險防控機制研究[D].廣西大學,2008

⑤曲秋實.基于logit模型的商業銀行個人信用風險評估[J].商業經濟,2010(12)

⑥丁穎麗.三層計算構架中Logistic回歸分析的設計與實現[D].東華大學,2008

⑦劉璐.廣義矩估計的理論與應用研究[D].天津大學,2002

⑧王云端.銀行信貸風險識別的五級分類法應用研究[D].東北大學, 2006

（作者單位：陜西師范大學國際商學院 陜西西安 710000）

F830.589

A

1004-4914（2014）05-166-03