自主定向系統快速對準方法研究

孟樂中，何 英

（貴州航天控制技術有限公司，貴陽550009）

自主定向系統快速對準方法研究

孟樂中，何 英

（貴州航天控制技術有限公司，貴陽550009）

摘要：提出了一種基于動基座、大傾角的初始對準方法，研究了粗對準數學模型、羅經回路精對準數學模型以及捷聯航姿解算數學模型,并實現樣機設計。仿真結果和樣機測試情況驗證了該方法的快速性與精度，可為車載系統自主快速對準提供理論借鑒,具有一定工程應用價值。

關鍵詞：自主定向系統；快速對準；仿真；試驗

0　引言

初始對準從控制角度上講就是施加一定的控制角速度把數學平臺轉向期望的位置（與地理坐標系重合），它是按誤差方程進行控制的。自主初始對準技術是慣性技術的運用，在工程實現上具有一定的挑戰性，并且現代戰爭對其測試精度、對準時間、使用環境以及工作可靠性等方面要求越來越嚴格，但由于與其它初始值測定方法相比具有較大優勢，因此自主初始對準技術的研究已成為國內外慣性技術領域的研究重點。國內外在捷聯慣導系統的初始對準方面已做了大量的工作。上世紀中葉，美國的Baziw和Leondes在研究主從傳遞對準方法時采用了卡爾曼濾波最優估計理論。80年代Porat和Bar-Itzhack針對發射車加速度對自主初始對準精度的影響進行了研究分析。90年代Goshen-Meskin和Bar-Itzhack從控制理論的角度出發，提出分段定常系統代替時變動態系統進行可觀測性分析的PWCS理論，給動基座初始對準的可觀測性分析提供了理論依據和分析。國內在對準方面也做了很多研究，北京航空航天大學研究了幾種可觀測性分析方法，并將這些方法應用于慣導初始對準的可觀測性分析中，得出了一種更有效的確定不可觀狀態的方法，提出了一種新的自適應濾波方案。上海交通大學在艦載武器的初始對準時采用了參數不確定系統的魯棒濾波方法，從產品測試精度得出魯棒濾波的性能優于卡爾曼濾波的結論。此外，南京航空航天大學首次在慣性導航系統使用BP神經網絡理論進行初始對準等研究。目前的國內外研究重點是在尋求顯著提高對準精度同時縮短對準時間的手段，導出更有效的慣導系統誤差模型及初始對準算法，以提高對準精度[1]。

自主定向系統安裝在某武器系統發射架的末端，3min內完成自主對準并進入導航狀態，對準后實時提供發射架的姿態角（即方位角、俯仰角和橫滾角），并將發射架的姿態角傳遞給導彈，即完成了導彈的初始方位和姿態裝訂。自主定向系統成功研制對提高武器系統的機動性來說具有重要意義。它實現了武器系統停車就打甚至邊打邊走的可能性。

發射車在野外使用，自主定向系統使用環境比較嚴酷。自主定向系統在使用過程中會受到各種外界干擾如發射車發動機的震動、測試人員的走動、在野外陣風沙擾動（自主定向系統在不大于20m/s的陣風條件下能夠正常工作）及發射車的機動等，這些干擾對自主定向系統對準產生影響，加大了自主定向系統的對準難度。根據自主定向系統使用環境，提出采用基于重力加速度作為參考矢量的解析粗對準算法和經典的羅經法精對準算法，并通過仿真和樣機實施驗證了算法的有效性。

1　自主定向系統對準技術模型

1.1基于重力加速度解析粗對準

1.1.1物理意義

基于重力加速度的解析式粗對準原理如下：在初始尋北計算過程中，選用慣性坐標系作為參考基準，同時將加速度計的輸出值在參考坐標系中投影。當發射車處于靜止狀態時，在導航坐標系中發射車位置不會改變；但在慣性坐標系中，由于地球自轉的原因，地球重力加速度會在以地球自轉軸為主軸的錐面內發生緩慢的變化，變化情況如圖1所示。因此，在不同時刻(間隔不為24小時的整數倍時)地球重力加速度在慣性坐標系內是不重合的。地球以恒定的角速度轉動，當對準時間測量準確時，重力加速度在慣性空間內的方向改變包含了地球北向信息，而基于重力加速度解析粗對準正是利用了這一基本原理。

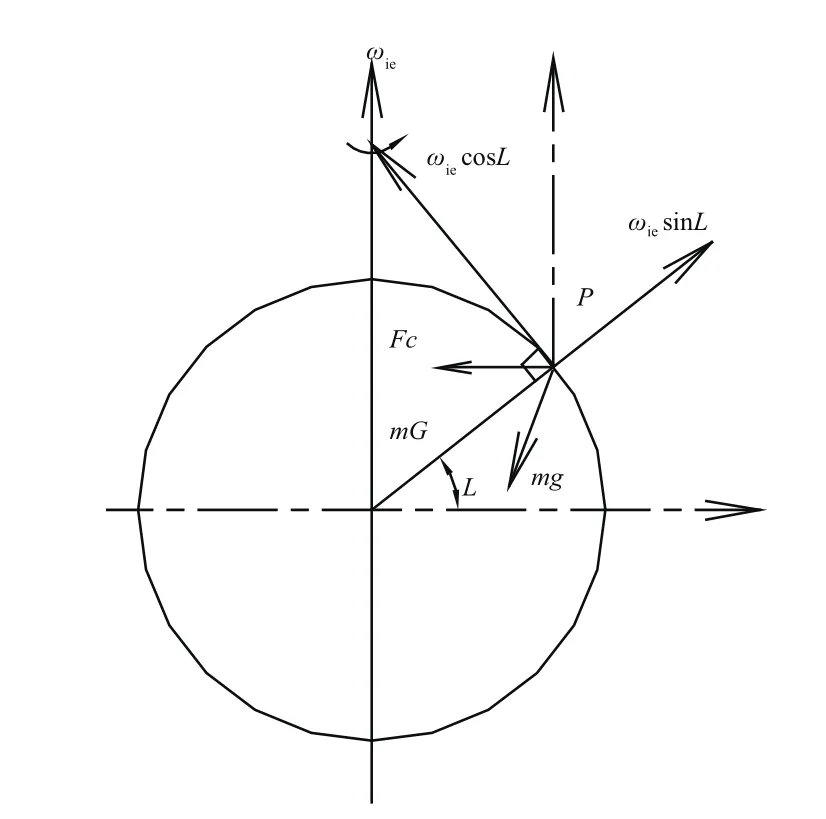
圖1　慣性坐標系中地球重力加速度矢量Fig.1 Gravity acceleration vector of the Earth in an inertial coordinate system

1.1.2對準算法

坐標系的定義：①經線地球坐標系(oxe0ye0ze0)，原點o在地球中心，ze0指向地球自轉軸，xe0在赤道平面內并指向發射車在初始對準時刻所在位置的經線，ye0滿足右手定則，該坐標系與地球固連，隨地球轉動；②經線地心慣性坐標系(oxi0yi0zi0)，在初始對準時刻將oxe0ye0ze0在慣性空間凝固后所得到坐標；③慣性坐標系(oxi0yi0zi0ib0)，它是在t0時刻將發射車坐標系b經慣性凝固后得到，其中t0為粗對準的起始時刻；④導航坐標系(oxnynzn),用于導航解算的參考坐標系，本文導航坐標系為東北天。通過轉換得到發射車坐標到導航坐標的轉換，表達式為：

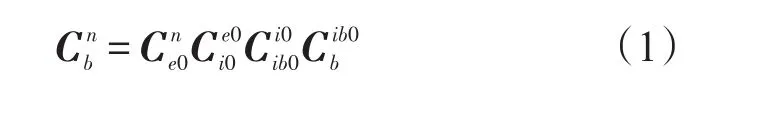
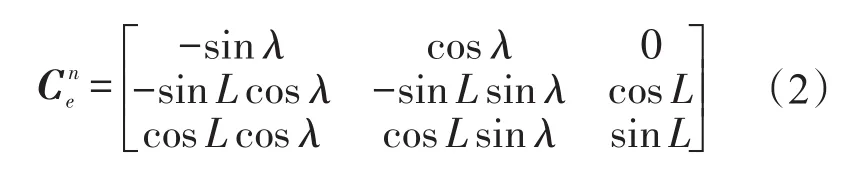
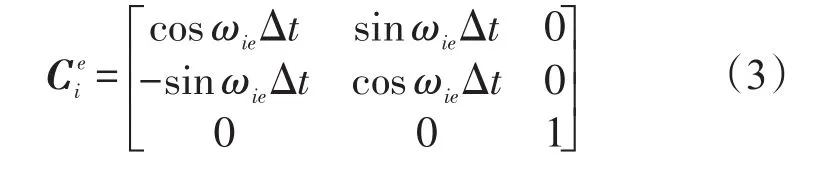
式中ωie為地球自轉角速度，為載體坐標系b和慣性基座坐標系ib0之間的方向余弦矩陣，這個矩陣可以利用陀螺輸出，通過四元數更新求解獲得。遞推更新計算的初始矩陣是單位矩陣I。

發射車在外部風擾的影響下，存在一定幅度搖擺和垂蕩、縱蕩、橫蕩運動。此時，加速度計的輸出投影到慣性基座坐標系ib0為：

當載體受線性位移運動干擾時，例如風擾引起的垂蕩、縱蕩、橫蕩運動，可以近似為周期變化，在一段較長時間段內這種干擾加速度的積分值為零。在時間段t0到tk內，真實的速度值為：

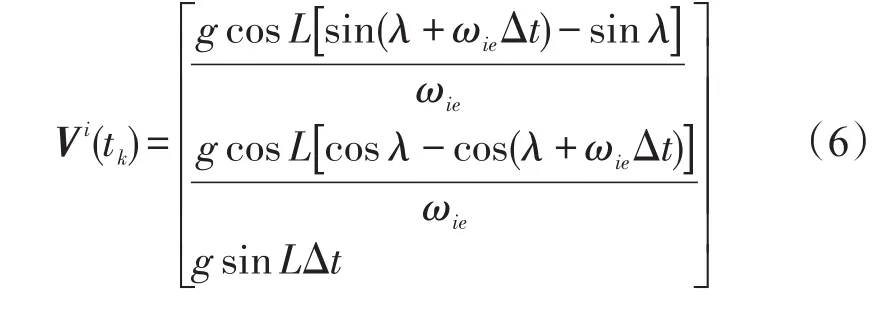
其中積分區間為Δt=tk-t0。

同時，對式（5）在時間段t0到tk內積分得到計算速度值為：

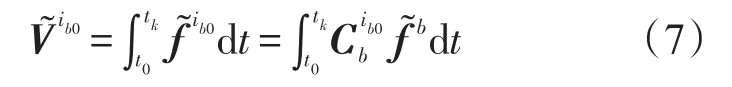
由真實的速度值與計算速度值可得：

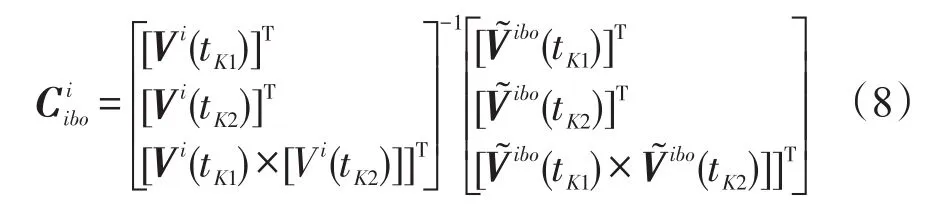
Vi可以通過式（6）計算得到，可以通過式（7）計算得到，再由式（8）可以計算出。通過式（2）和式（3）可以直接計算出和。利用四元數更新算法，可以遞推計算出，最后將它們代入到式（1）中計算出捷聯姿態矩陣。自主定向系統粗對準原理圖如圖2所示。

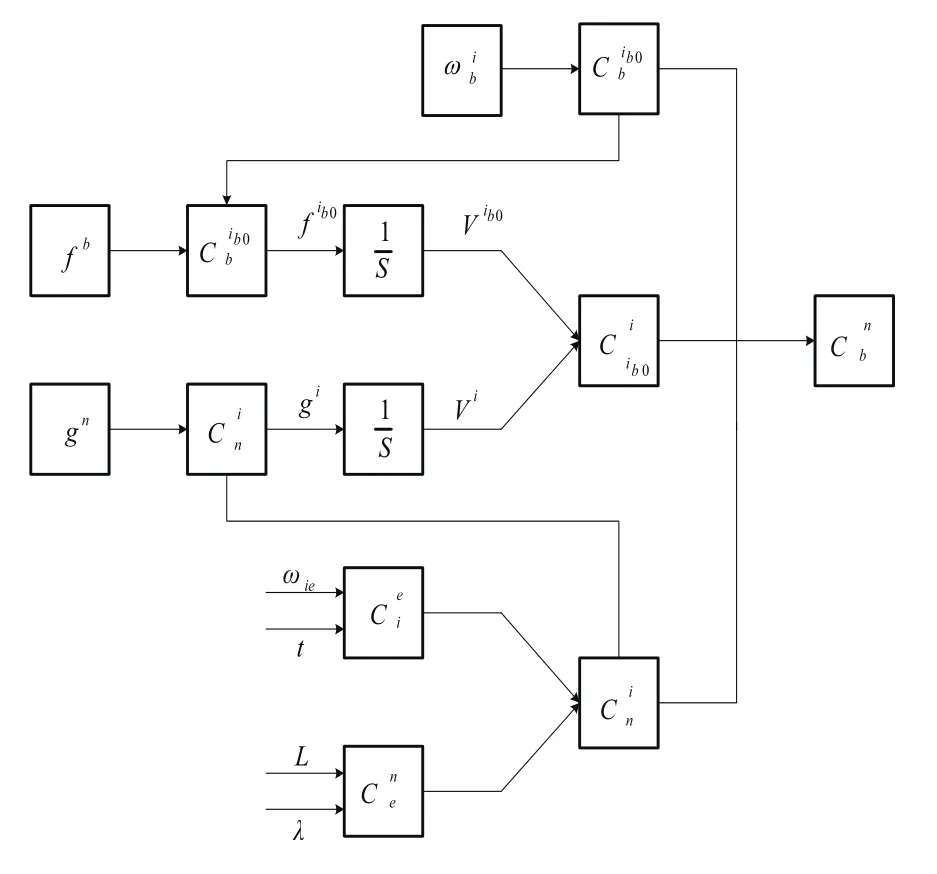
圖2　自主定向系統粗對準原理圖Fig.2 Coarse alignment schematic diagram of autonomous orientation system

1.2羅經回路精對準算法數學模型

羅經方位精對準是利用羅經效應尋北的原理來進行方位對準[2]。在水平對準的前提下，當平臺坐標系的北向軸與真實北向存在誤差角?z時，地球自轉角速度Ω在地理北向投影為ΩcosL，在平臺的東向也會出現投影，其值為ΩcosLsinφz。這個角速度引起俯仰誤差角?x。當俯仰誤差角的存在時，平臺的水平方向上就會出現重力加速度g的投影，進而引起速度誤差。這樣就可以通過速度誤差作為控制信號，來控制平臺的航向誤差角?z，使得?z減小到所需的范圍內，即構成所謂羅經效應[3]。圖3為應用羅經回路原理所設計的北向回路及羅經方位回路對準原理圖。

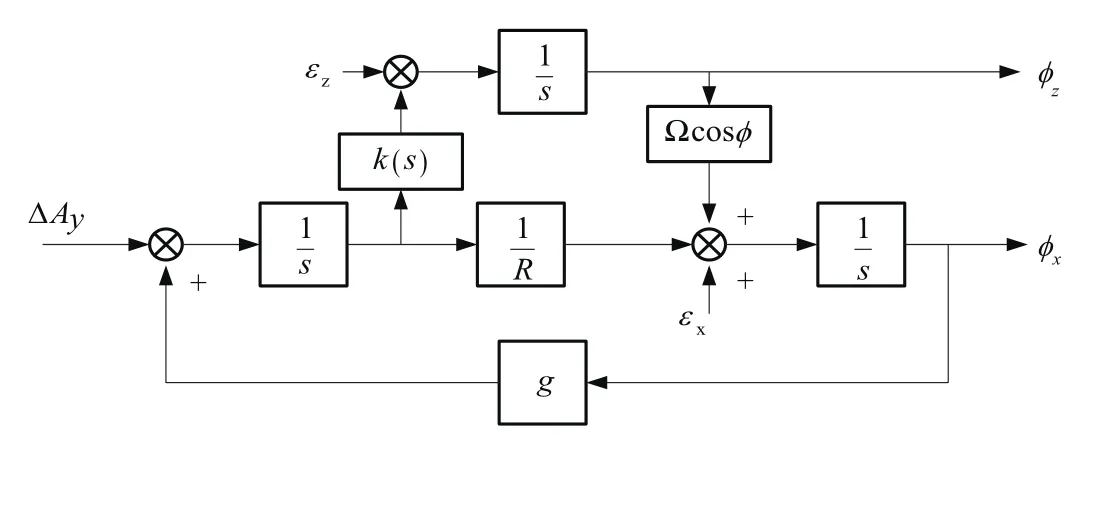
圖3　羅經回路原理圖Fig.3 Schematic diagram of compass loop

圖中R為地球半徑，εx、εy、εz表示等效的東向、北向和天向的陀螺漂移，ΔAx、ΔAy為等效東向和北向加速度計零偏，?x為平臺俯仰誤差角，?y為平臺橫滾誤差角，?z為方位誤差角。k(s)為速度控制環節。使用時針對系統的需要，合理的加入阻尼和增益，調整系統特性。

圖4為東向水平回路設計原理圖，圖5為北向水平回路和方位回路原理圖。

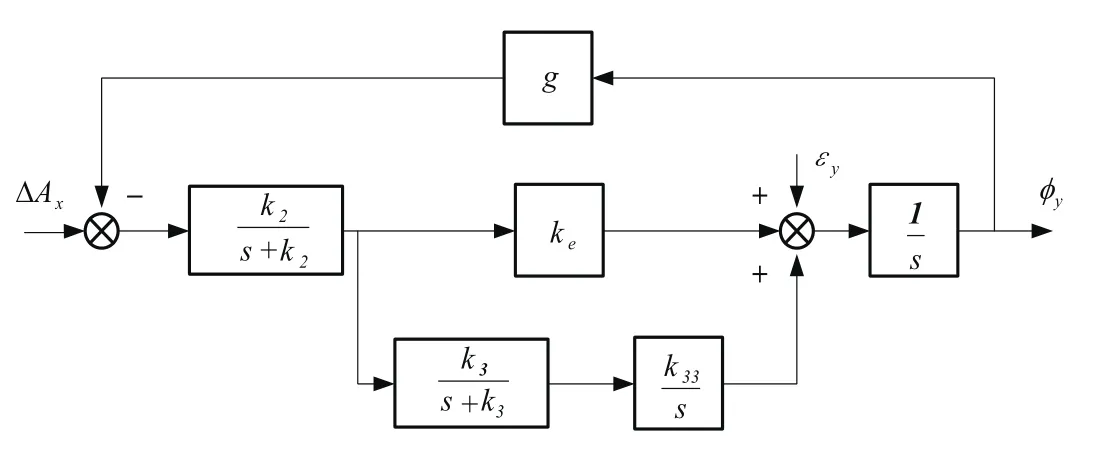
圖4　東向水平回路原理圖Fig.4 Schematic diagram of east loop

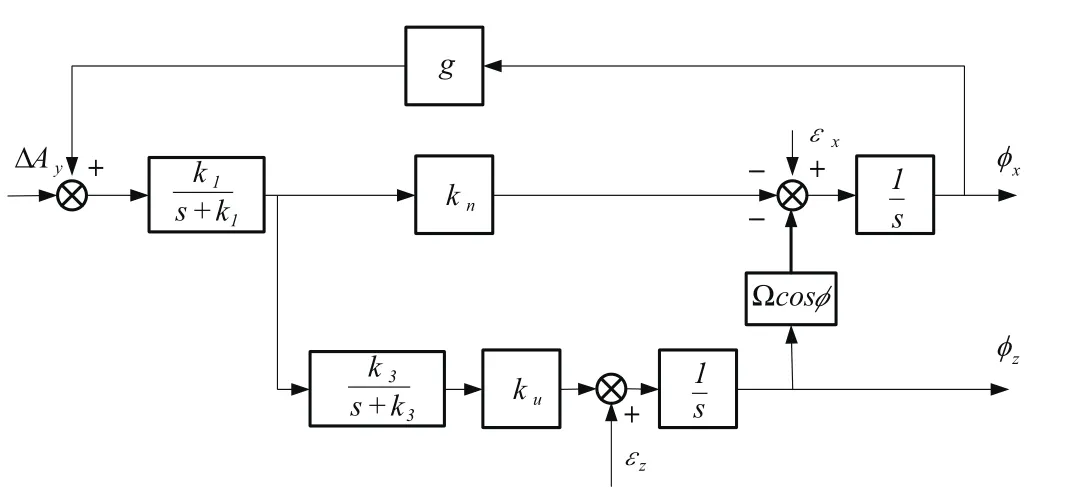
圖5　北向水平回路原理圖Fig.5 Schematic diagram of north loop

1.3姿態矩陣更新計算方法

在姿態解算過程中，由于剛體轉動的不可交換性而產生的圓錐誤差是不可避免的，為提高姿態解算精度必須采取相應措施減少誤差。旋轉矢量修正算法是克服圓錐誤差的有效途徑，本方法通常情況下使用陀螺測得的角增量信息來進行修正的；但目前國內使用的光纖陀螺輸出信號為角速率，如通過角速率積分得到角增量再進行修正將會帶來計算誤差。為了減少計算誤差，在姿態解算時直接利用角速率信號作為旋轉矢量算法的修正信號。本方法以角速率作為算法的輸入信號，用角速率表示旋轉矢量的微分方程，以角速率的叉乘項擬合圓錐誤差項，并且在典型圓錐環境中計算多項式的系數。基于角速率的圓錐誤差補償算法，應用于自主定向系統姿態矩陣的更新，有效得補償了高動態環境下的圓錐誤差，提高自主定向系統的姿態測量精度。

確定姿態更新周期H=tm-tm-1，H等于N倍的光纖陀螺采樣周期h=tl-tl-1。利用光纖陀螺輸出計算出發射車相對于慣性坐標系的角速度計算旋轉矢量增量Δ?。其具體步驟為：

由光纖陀螺輸出的輸出計算Δ?中的慣性可測項，即角增量α。每個姿態更新周期H內已知N+1個光纖陀螺采樣角速度ω0、ω1、...ωn；則姿態更新周期H內的角增量α為：

式中：

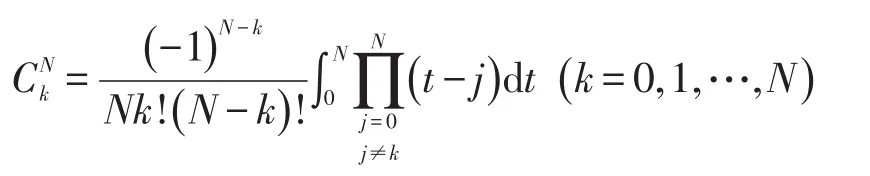
由光纖陀螺輸出的輸出計算Δ?中的非慣性可測項，即圓錐補償項β；每個姿態更新周期H內已知N+1個光纖陀螺采樣角速度ω0、ω1、...ωn。

在姿態更新周期H內，圓錐補償項β由光纖陀螺采樣角速度叉乘項的線性組合來計算。

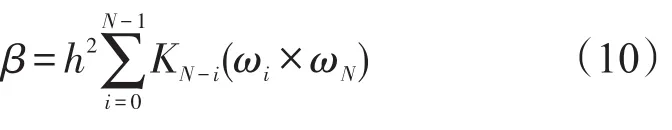
式中KN-i為優化系數，在典型圓錐環境中確定。

得到的姿態更新周期H內角增量α，與姿態更新周期H內圓錐補償項β相加，得到姿態更新周期H內旋轉矢量增量Δ?。

設置N=3，陀螺在t時刻采樣角速度ω0，并且每個姿態更新周期H，在t+H/3、t+2H/3、t+H時刻采樣ω1、ω2、ω3；得到姿態更新周期H內旋轉矢量增量Δφ為：

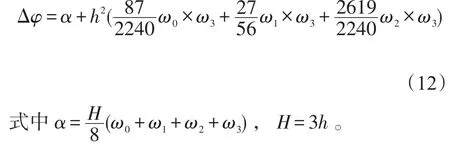
以上是基于角速度計算旋轉矢量增量的過程。

計算得到旋轉矢量的增量Δφ后，通過旋轉矢量與四元數的關系，得到姿態更新周期H內姿態更新四元數q(H)。

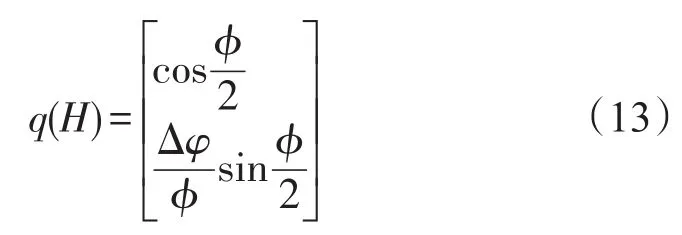
由姿態四元數更新方程更新姿態四元數。

式中Q(tm)、Q(tm-1)分別表示載體在tm、tm-1時刻的姿態四元數。

以光纖陀螺的角速度作為算法的輸入時，直接利用角速度計算旋轉矢量，計算四元數，避免了常規算法角速度到角增量的積分誤差，其性能優于傳統算法。

2　算法仿真分析

2.1仿真環境設置

為了驗證本方法的可行性，利用仿真軟件進行仿真，仿真條件如下：

1）地理位置：緯度L=26.5°、經度λ=106.5°，高度h=1070m；

2）陀螺常值漂移0.02(°)/h、隨機游走誤差0.01(°)h12；加速度計常值偏置1×10-4g；

3）基座晃動條件：在自主定向系統三個方向上加入頻率 f=1Hz，幅值A=3°的角振動；

4）姿態初始值：俯仰角為55°、橫滾角為0°，方位角0°。

仿真時間180s，其中，前30s進行粗對準，粗對準結束后，再轉入進行精對準。各姿態誤差角如圖6所示。

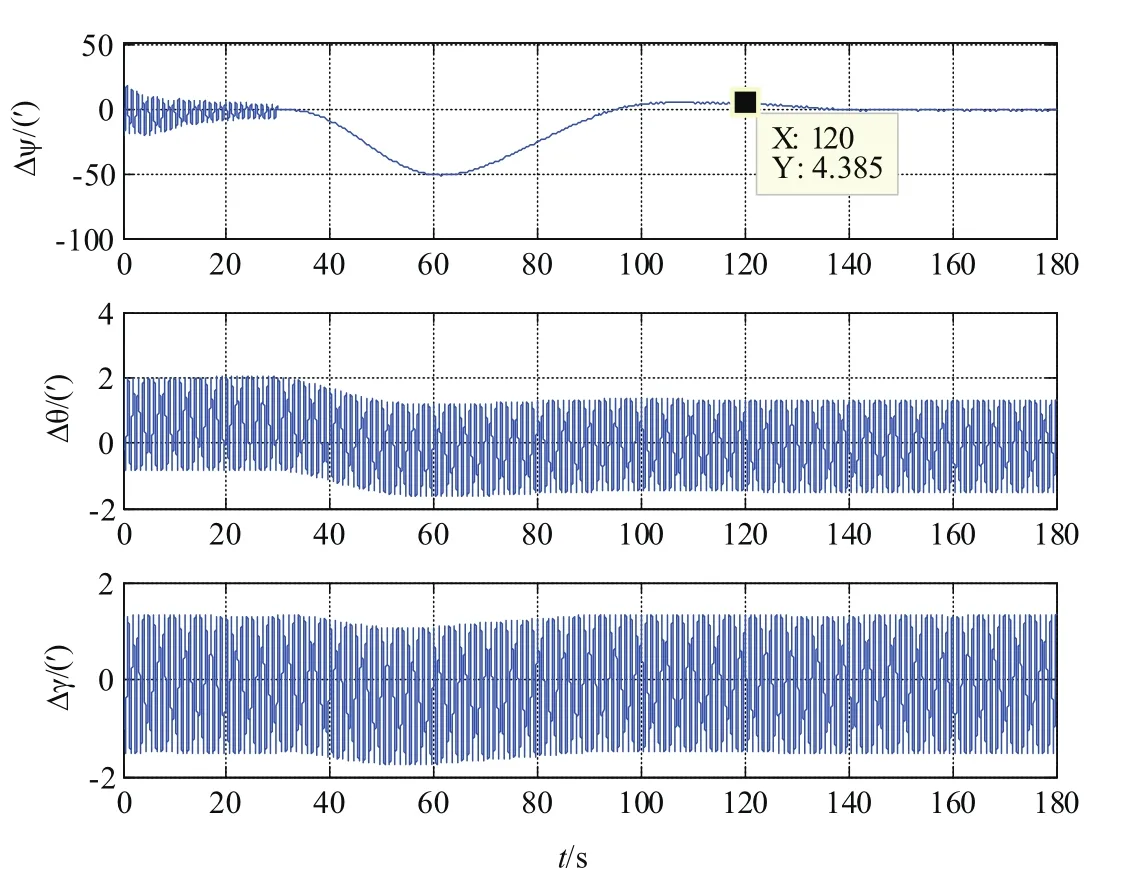
圖6　三軸搖擺時180s對準誤差Fig.6 Alignment error over 180 seconds upon three axes swaying

由仿真分析可知，對于姿態調平，羅經對準法具有較高的抗外界擾動能力，能夠在短時間內收斂至較高精度，在仿真時間60s后，東向誤差角和北向誤差角穩定在一定范圍之內，最大跳動量在0.05°以內。因此，羅經姿態調平在工程中被廣泛應用。

對于方位對準，抗外界擾動效果較差，在進入羅經方位對準時有一定的超調，但在120s時，航向誤差收斂到0.1°以內。在180s時，航向誤差收斂到0.05°以內。

3　試驗驗證

在完成了自主定向系統的方案論證和理論研究后公司開展了原理樣機研制工作。2014年3月在公司慣導試驗室對樣機進行性能測試：樣機測試測試條件為俯仰角初值為55°、橫滾角初值為0°、每隔60°進行一次對準，同時在航向和俯仰方向施加頻率 f=1Hz，幅值A=3°的角振動。測試數據見表1。

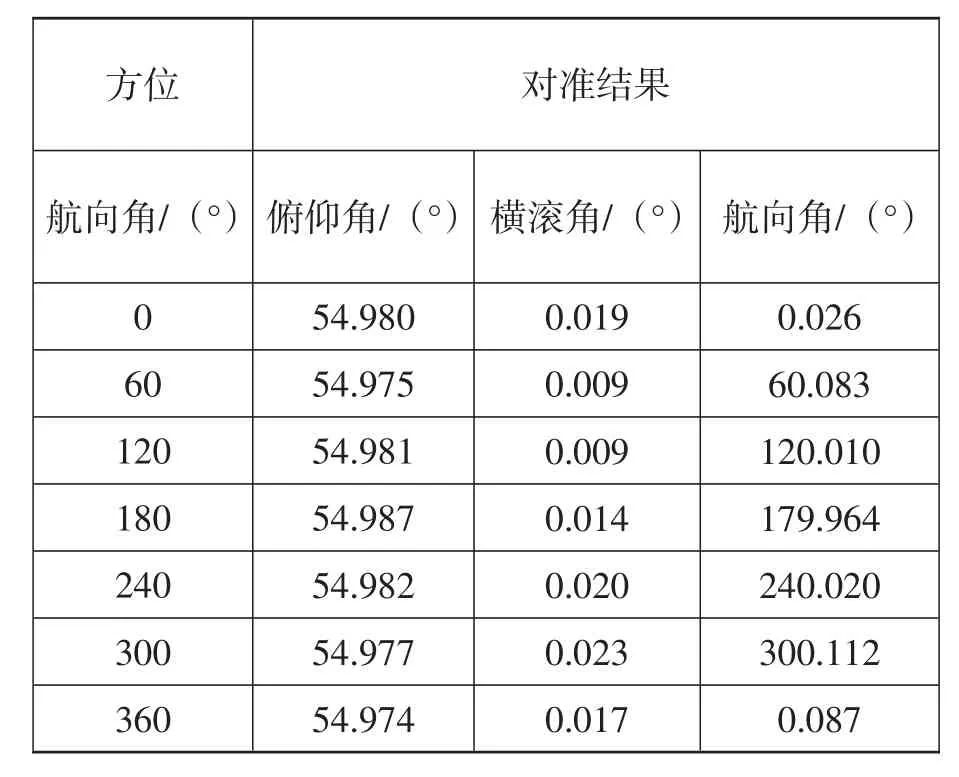
表1　測試結果Tab.1 Results of the test

從表中測試的數據可以得出，在上述的條件下，在3min內航向角最大誤差為0.112°、俯仰角最大誤差為0.02°、橫滾角最大誤差為0.023°，優于發射車的指標要求。

4　結論

本文首先對自主定向系統可能受到的干擾進行深入的分析，建立了新的動基座對準方法和姿態更新方法，該方法能夠完全不依賴任何外部信息自主實現了動基座初始對準功能。

仿真結果和樣機測試情況表明，該方案切實可行。利用光纖陀螺進行發射車的初始姿態測試在國內屬于首創，而且對準條件惡劣：要求在陣風等干擾條件下、俯仰角為55°、3min完成對準，該自主定向系統成功研制在慣性領域中是一項技術突破。

參考文獻

[1]聶莉娟.捷聯慣導系統初始對準濾波技術研究[D].工學碩士學位論文，哈爾濱工程大學,2004,1.

[2]王進,練軍想,吳美平.捷聯慣導系統初始對準方法比較[J].國防科技大學機電工程與自動化學院.

[3]秦永元.慣性導航[M].北京：科學出版社.

中圖分類號：TP273

文獻標志碼：A

文章編號：2095-8110（2014）03-0031-06

收稿日期：2014–05–16；

修訂日期：2014–09–27。

作者簡介：孟樂中（1975–），男，碩士，主要從事慣性導航技術方面研究。

Research on RapidAlignment Method forAutonomous Orientation System

MENG Le-zhong,HE Ying
(GuizhouAerospace Control Technology Ltd.,Guiyang 550009,China)

Abstract：The initial alignment method is proposed based on moving base and large inclination.It makes a study on the mathematical models of coarse alignment,compass loop fine alignment and strap-down attitude determination.And the prototype design is realized.The rapidity and accuracy of the proposed method is proven by simulation results and prototype tests.This provides a theoretical basis for the autonomous rapid alignment of the vehicle-mounted system and has a certain engineering value.

Key words:Autonomous orientation system；Rapid alignment Simulation；Test