帶落角約束的圓弧比例導引律和偏置比例導引律的研究

周 魯，宋建梅，黃 嵐

（飛行器動力學與控制教育部重點實驗室，北京理工大學宇航學院，北京100081）

帶落角約束的圓弧比例導引律和偏置比例導引律的研究

周 魯，宋建梅，黃 嵐

（飛行器動力學與控制教育部重點實驗室，北京理工大學宇航學院，北京100081）

摘 要：為了實現導彈以一定落角命中目標，研究了兩種帶有落角約束的圓弧比例導引律和偏置比例導引律。首先建立彈目相對運動數學模型和框架動力學數學模型，然后闡述了兩種導引律的基本原理，接著對導彈在三維空間內攻擊靜止與運動目標進行數學仿真試驗，仿真實驗證明兩種導引律都能以較小的脫靶量和期望落角命中目標，最后從原理上和仿真實驗上對兩種導引律進行了對比研究。

關鍵詞：圓弧制導；偏置比例導引；落角約束

0　引言

比例導引律形式簡單，技術上易于實現，其彈道比較平直，能對付機動目標，并且導引精度高，所以被廣泛應用[1-3]。然而很多導彈在命中目標時，不僅希望得到較小的脫靶量，還希望導彈能夠以最佳角度命中目標，以發揮戰斗部的最大效能，實現最佳毀傷。比如當目標為重裝甲的坦克或者攜帶危險載荷的飛行器時，導彈擊中目標的角度就顯得尤為重要。Kim Grider[4]首先對落角約束比例導引開展了研究，此后很多學者在不同的應用背景下，提出了多種具有落角約束的導引律[5]。迄今為止，研究較為廣泛的導引律有三類：一類是跟蹤某條特殊軌跡來控制末速度方向的幾何曲線導引律，例如圓弧導引律[6-8]；另一類是在傳統比例導引律的基礎上進行改進，例如變系數比例導引律和添加一個時變偏置項的偏置比例導引律[9]；第三類是以現代滑模變結構理論為基礎的變結構比例導引律[10]。

本文基于半捷聯尋的制導系統對圓弧比例導引律和偏置比例導引律進行研究，把俯仰平面內的落角約束擴展到三維空間中的命中速度方向約束。本文首先介紹了相關坐標系和它們之間的轉換關系，并建立了半捷聯尋的制導系統數學模型；然后給出了圓弧比例導引律和偏置比例導引律和推導過程，從機理和使用兩方面對兩種導引律進行了對比。最后以導彈攻擊三維空間內的地面靜止目標和低速運動目標為例，對兩種導引律數學仿真試驗，從彈道、法向過載、落角誤差、脫靶量等方面進行了比較。

1　相關坐標系的定義和轉換

1）地面坐標系Axiyizi：地面坐標系是與地球表面固連的坐標系。坐標系原點A選取在導彈初始位置的質心處；Axi軸指向可以是任意的，Ayi軸位于包含Axi軸的鉛垂面內，垂直于Axi軸，向上為正，Azi軸與其它兩軸構成右手坐標系。

2）彈體坐標系Oxbybzb：坐標系的原點O取在導彈的質心上；Oxb軸與導彈縱軸重合，指向頭部為正；Oyb軸位于導彈縱向對稱面內垂直于Oxb軸，向上為正；Ozb軸與其他兩軸構成右手坐標系。

3）外框坐標系Oxg1yg1zg1：原點O取在探測器中心，由于本文采用的彈體為質點模型，因此探測器中心即為彈體質心，Oxg1垂直于外框架平面，指向目標方向為正，Oyg1軸與彈體坐標系Ayb軸重合，Ozg1軸位于彈體坐標系Oxbzb平面內，與其他兩軸構成右手坐標系。

4）內框坐標系Oxgygzg：原點O取在探測器中心，Oxg軸與光軸指向相同，指向目標方向為正，Ozg軸與外框坐標系Ozg1軸重合，Oyg軸在外框坐標系Oxg1yg1平面內，與其他兩軸構成右手坐標系。內框坐標系又稱為光軸坐標系。

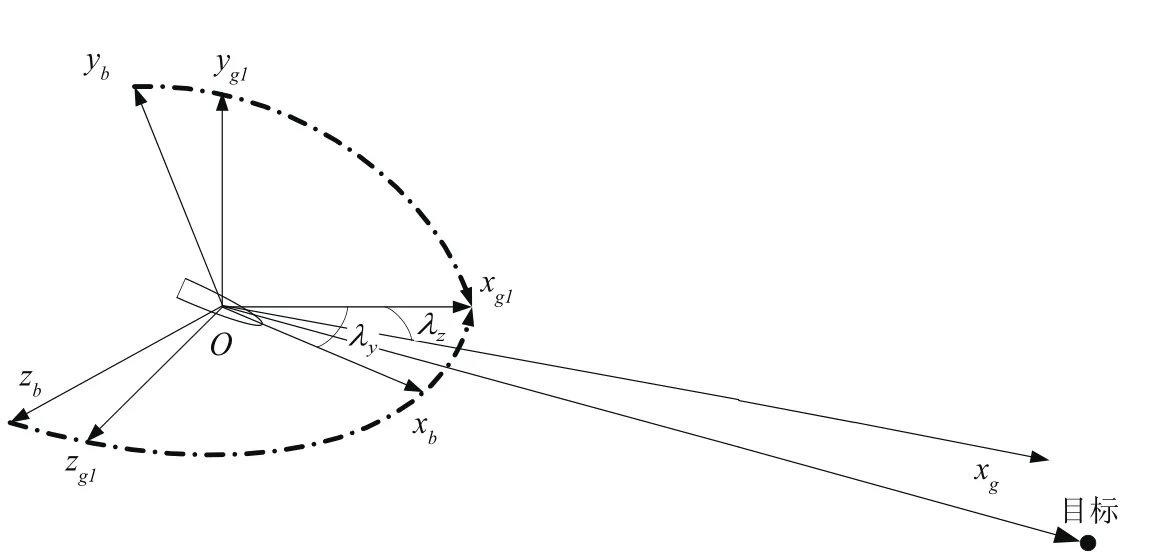
圖1　導引頭幾何示意圖Fig.1 Geometry of the seeker

彈體坐標系繞Oyb軸旋轉λy角，便可得到外框坐標系，則彈體坐標系到外框坐標系的轉換矩陣Tb→g1為：

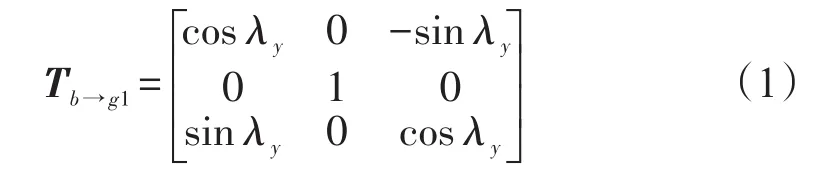
外框坐標系繞Ozo軸旋轉λz角，便可得到內框坐標系，則外框坐標系到內框坐標系的轉換矩陣Tg1→g為：

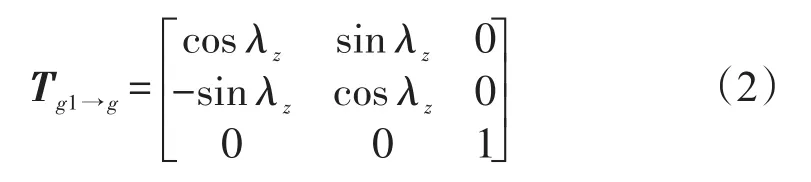
則彈體坐標系到內框坐標系的轉換矩陣Tb→g為：

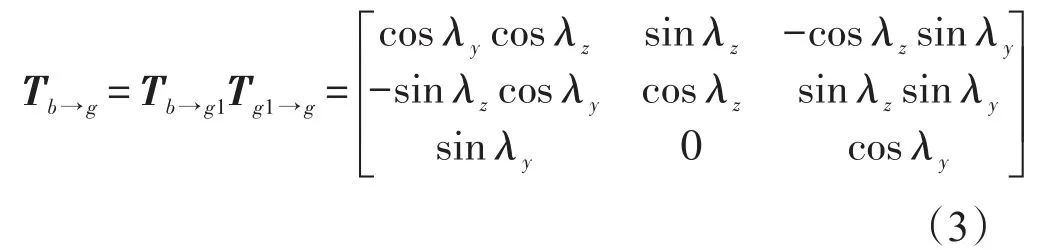
地面坐標系到彈體坐標系的轉換矩陣Ti→b為：

式中，?,ψ,γ分別為彈體俯仰角、偏航角與滾轉角。

2　彈目相對運動數學模型和框架動力學

2.1彈目相對運動數學模型

在慣性系下建立彈目相對運動模型如下：

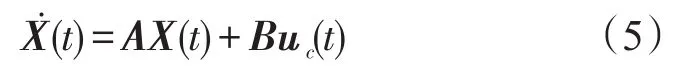
其中：

式中XR(t)∈R3為彈目相對位置，VM(t)∈R3為導彈的速度，VT(t)∈R3為目標的速度。 uc是導彈法向加速度指令，滿足如下約束：

2.2半捷聯尋的制導系統框架動力學模型

本文假設導引頭框架動力學模型如下所示：

式（8）中kg為常數，αz和αy為視覺傳感器的光軸需要轉動的俯仰角和偏航角，設為彈目相對位置在彈體坐標系下的投影，αz為與彈體系Oxbzb平面間的夾角，指向Oxbzb平面上方時αz為正，反之為負；αy為在Oxbzb平面內的投影與Oxb軸之間的夾角，迎Oyb軸俯視，若其投影位于Oxb軸左側，則αy為正，反之為負。將框架坐標系下的彈目視線轉化到彈體坐標系下可得：

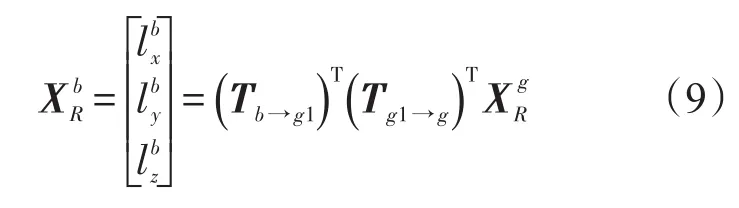
則αz與αy的計算公式為：

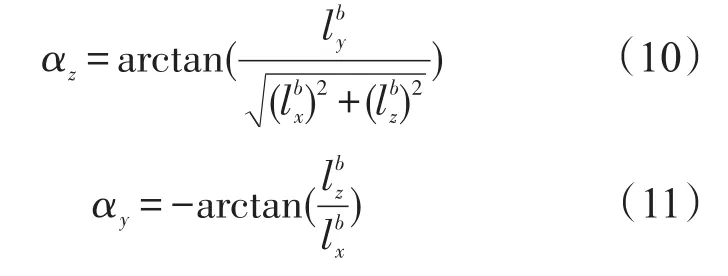
2.3導彈自動駕駛儀數學模型

假設自動駕駛儀為一階慣性環節，uc為導彈法向加速度指令， aM為導彈實際加速度，ρA=1TA，TA為一階慣性環節的時間常數，其動力學方程為：

3　圓弧導引律（CNG）

為了更好地闡述問題，定義運算符a|b為a在 b 方向上的投影，a|b⊥為a在b垂直方向上的投影。angle(a,b)表示a與b之間的夾角。

定義VD為導彈當前期望速度，VF為導彈最終期望的命中速度，VD和VF關于XR對稱，如圖2所示。ε表示VF與XR之間的夾角，λ表示VM與XR之間的夾角， fT表示視線角速度，eλ為VM和VD之間的夾角。假設目標固定，若能保證ε和λ嚴格相等，即VM與VD一致，那么導彈會以一個唯一確定的圓弧軌跡飛向目標，并以期望速度方向擊中目標[6]。

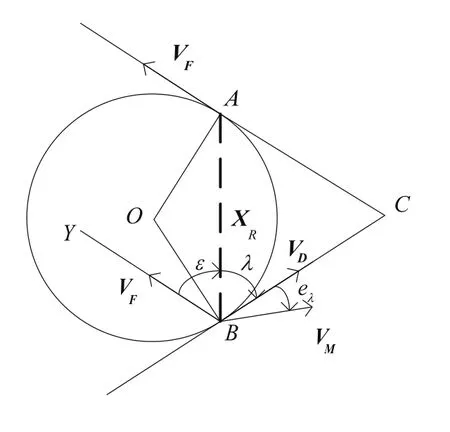
圖2　圓弧導引律示意圖Fig.2 Geometry of the CNG

式中：

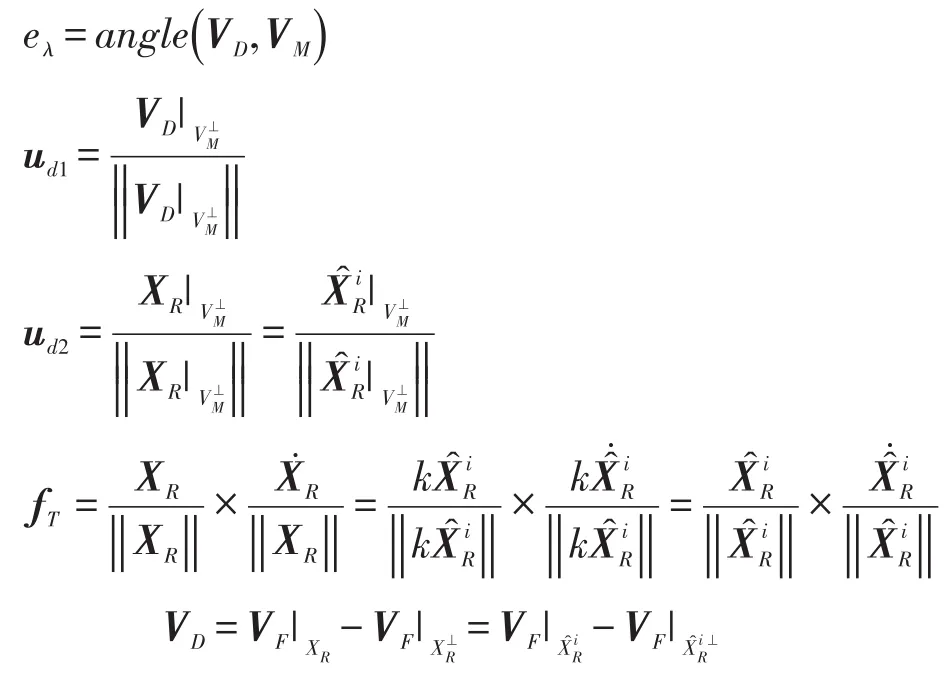
kp為比例系數，為在慣性坐標系下從攝像機光心指向目標成像點中心的向量，ud1，ud2為單位向量表示方向，式（13）中等號右邊第一項使VM轉向VD，第二項使導彈以圓弧軌跡逼近目標。

從圓弧導引律推導過程可以看出，圓弧導引律由兩部分項組成：第一部分是比例導引項，其作用是使導彈以較小的脫靶量命中目標；第二部分是導彈速度方向修正項，其作用是減小導彈當前速度方向與當前期望速度方向的偏差，使導彈最終以期望的角度命中目標。該導引律的主要優點是不需要知道彈目相對距離信息，只需要知道彈目視線的方向即可。

4　偏置比例導引律（BPNG）

BPNG的控制量由如下兩部分組成：

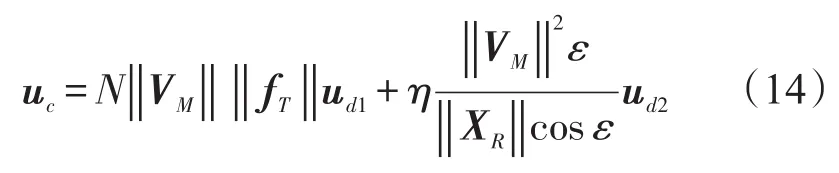
式（14）中η為設定的一個常數增益，ε為VF和 XR之間的夾角，λ為VM和 XR之間的夾角，N為一個時變增益，即：

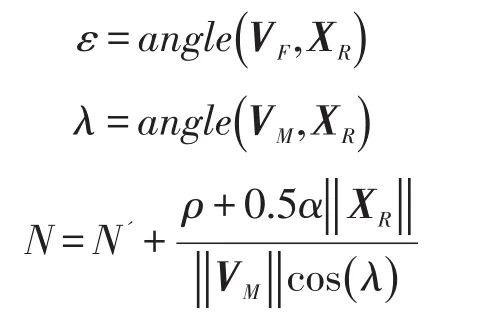
其中ρ為目標速度大小與導彈速度大小的比值，α和N'為設定的常數。由于比例導引項的作用是通過視線角速率信息使導彈命中目標，那么該控制量的方向ud1為：

偏置項的作用是修正導彈當前速度VM與彈目視線XR之間的夾角誤差ε，從而使導彈以期望的著角打擊目標，所以偏置項的控制量方向ud2為：

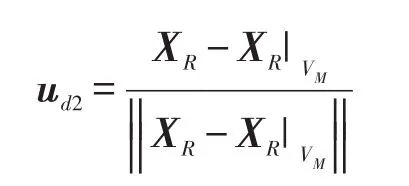
可見，偏置比例導引律是將傳統的比例導引系數改進為時變系數，同時添加了一個時變的偏置項，其作用是通過消除導彈速度與彈目視線方向之間的偏差來實現落角約束。偏置比例導引律與圓弧比例導引律的主要不同之處在于，偏置比例導引律需要知道彈目相對距離信息。

5　仿真驗證

5.1攻擊地面靜止目標

本節以導彈打擊三維空間內地面靜止目標為例，分別采用圓弧比例導引律和偏置比例導引律進行仿真實驗。假設導彈期望的命中速度方向為，即俯仰方向落角50.8°，偏航方向落角45°，自動駕駛儀時間常數TA=0.2s，框架角控制 器 增 益 kg=20， BPNG導 引參 數 為α=0.28,η=1.3,N'=2.9，圓弧比例導引律的導引參數kp=‖VM‖。仿真初始條件如表1所示。基于以上仿真條件得到的導彈各特征變量曲線如圖3～圖8所示。

表1　打擊地面靜止目標的系統初始狀態Tab.1 The initial state of system against ground target

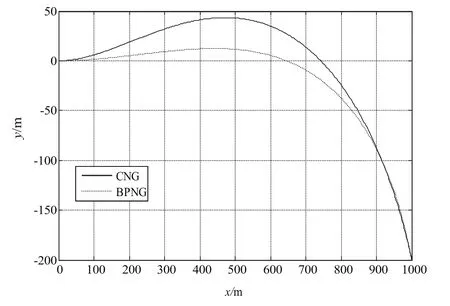
圖3　俯仰平面彈道曲線Fig.3 Trajectories in the pitch plane

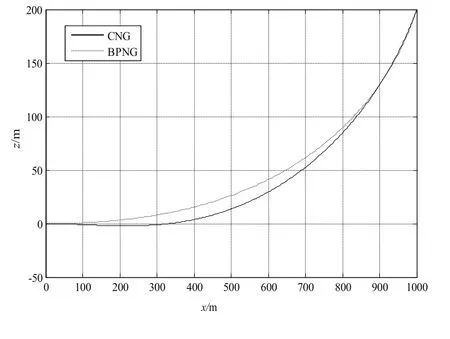
圖4　偏航平面彈道曲線Fig.4 Trajectories in the yaw plane

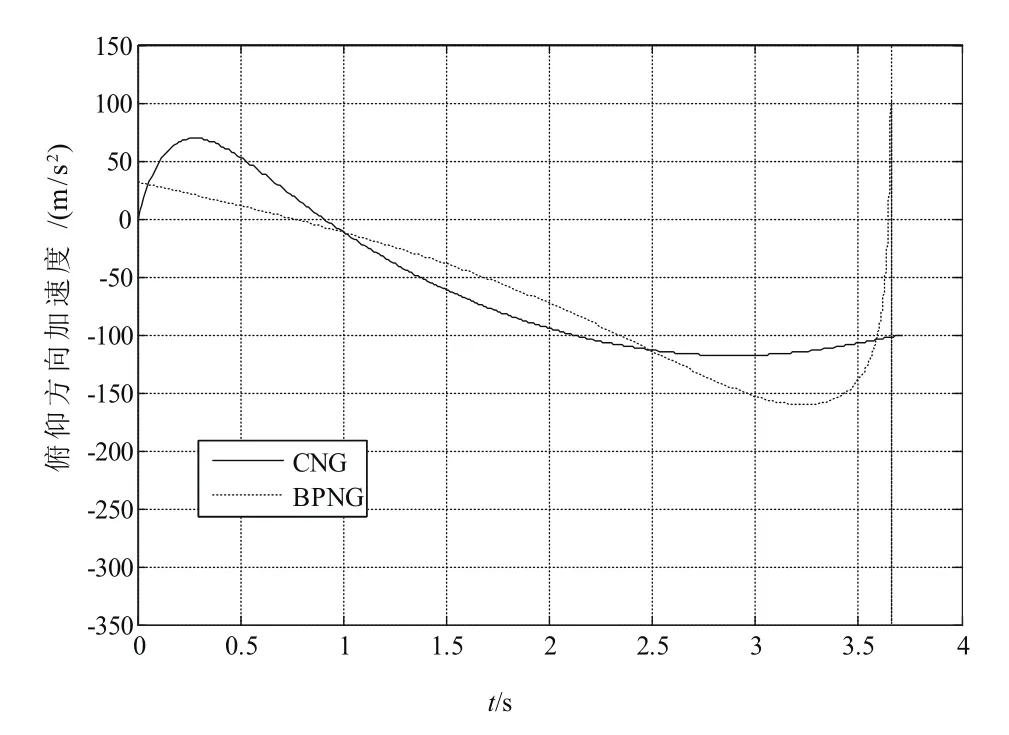
圖5　俯仰方向加速度Fig.5 Acceleration in the pitch plane

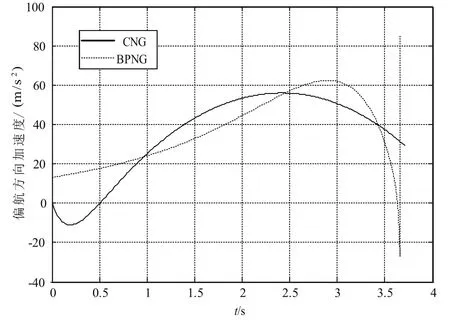
圖6　偏航方向加速度Fig.6 Acceleration in the yaw plane

圖7　俯仰落角曲線圖Fig.7 Attack angle in the pitch plane

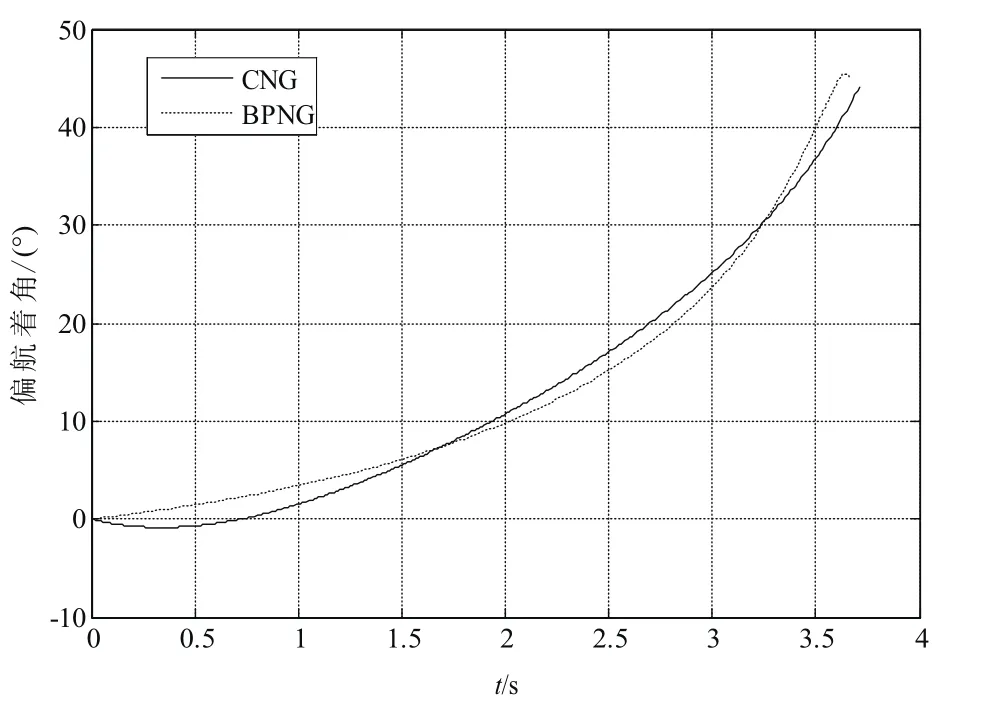
圖8　偏航著角曲線圖Fig.8 Attack angle in the yaw plane

由以上仿真結果可以看出，偏置比例導引律的彈道比圓弧導引律的彈道較平直。從過載上看，圓弧比例制導所需要的法向過載比偏置比例導引律較小，而且在末段偏置比例導引律的需用過載會急劇增加，在實際應用中會由于過載約束對制導精度產生影響。從制導精度上看偏置比例導引律的脫靶量為0.11m，俯仰方向的落角誤差為0.01°，偏航方向的著角誤差為0.02°；而圓弧導引律的脫靶量為1.11m，俯仰方向的落角誤差為0.72°，偏航方向的著角誤差為0.90°。

5.2攻擊地面運動目標

本小節假設目標在地面上以15m/s的速度沿x軸運動，其余仿真條件與5.1節相同。根據以上仿真條件得到的彈道曲線、過載曲線、VM與VF的夾角曲線分別如圖9～圖14所示。

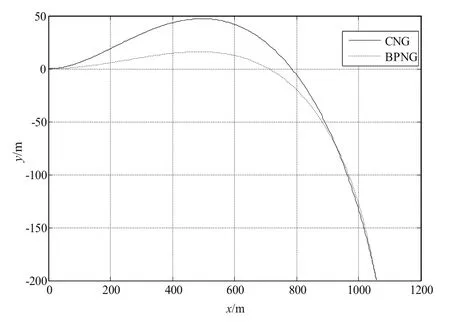
圖9　俯仰平面彈道曲線Fig.9 Trajectories in the pitch plane

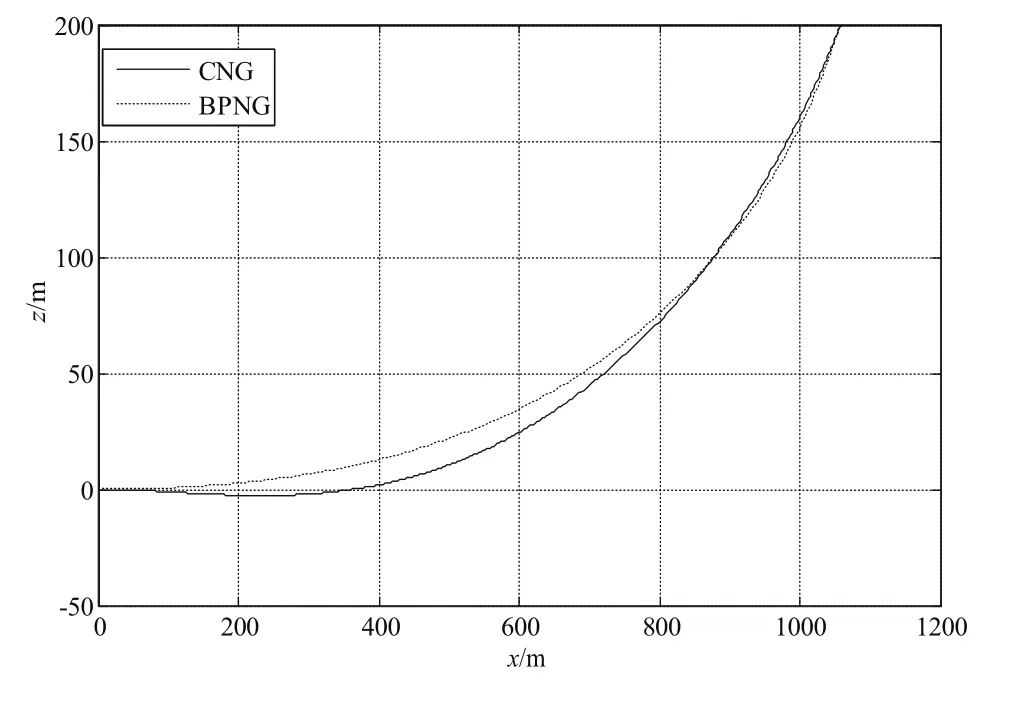
圖10　偏航平面彈道曲線Fig.10 Trajectories in the yaw plane

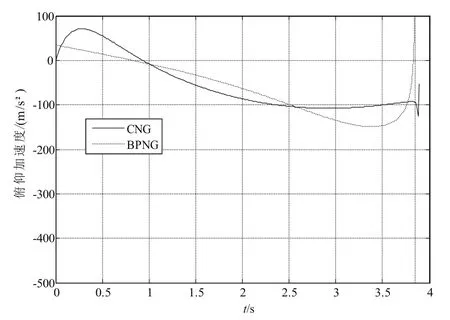
圖11　俯仰方向加速度Fig.11 Acceleration in the pitch plane

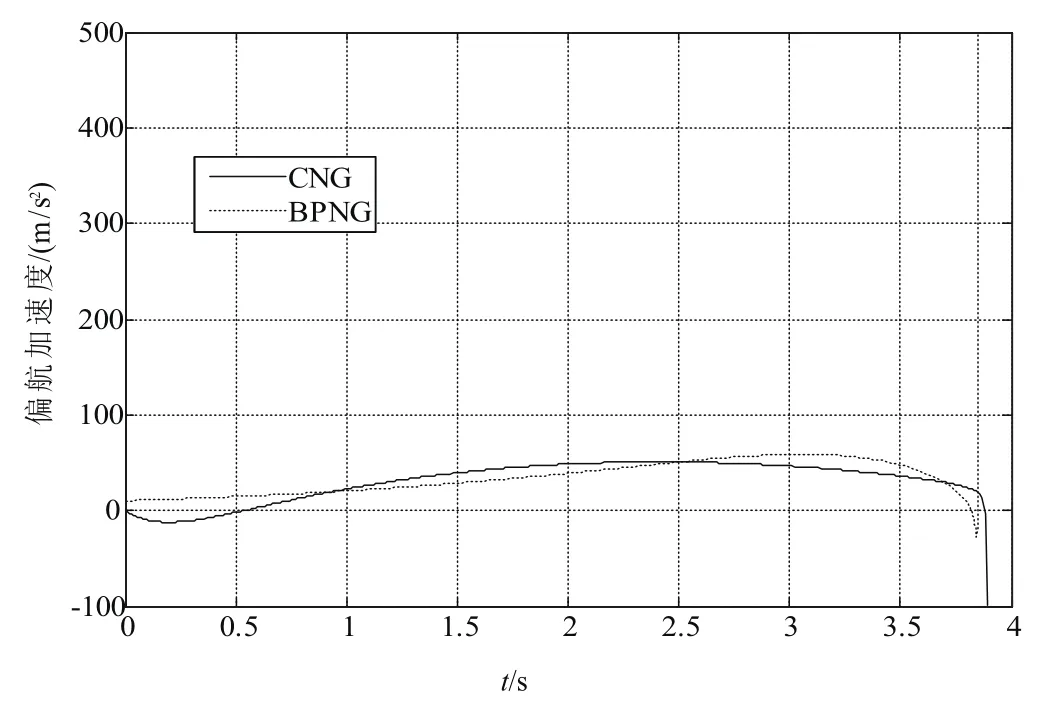
圖12　偏航方向加速度Fig.12 Acceleration in the yaw plane

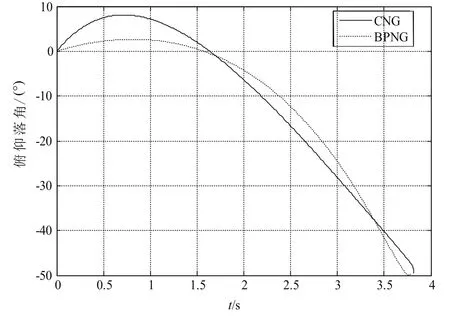
圖13　俯仰落角曲線圖Fig.13 Attack angle in the pitch plane

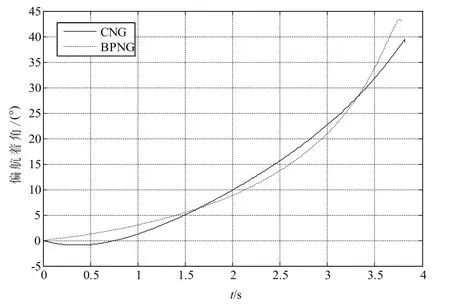
圖14　偏航著角曲線Fig.14 Attack angle in the yaw plane

根據以上仿真結果可以看出，偏置比例導引律的脫靶量為0.04m，俯仰方向的落角誤差為1.6°，偏航方向的著角誤差為3.1°。圓弧導引律的脫靶量為0.20m，俯仰方向的落角誤差為1.34°，偏航方向的著角誤差為6.17°。結合算例5.1，可以看出目標機動性對于圓弧比例導引律在精度上有很大的影響，而對偏置比例導引律的影響較小。

6　結論

本文針對半捷聯尋的制導系統，進行了帶落角約束的偏置比例導引律和圓弧比例導引律研究。研究表明，兩種導引律都能以較小的脫靶量和期望落角命中目標，其中圓弧比例導引律通過視覺導引頭提供的彈目視線方位信息來實現落角約束，彈目相對方位信息可通過成像平面中的目標成像位置間接獲取；偏置比例導引律則通過添加時變的偏置項來實現落角約束，需要已知彈目相對距離信息，但是半捷聯尋的制導系統不能提供此信息，只能通過其他方法獲取或者大致估算。從導彈三維空間內打擊目標的數學仿真可以看出：對于靜止目標，兩種導引律都能以很小的脫靶量和很高的落角精度命中目標；對于機動目標，目標的機動性對圓弧比例導引律的落角精度產生較大的影響，而對偏置比例導引律影響較小。從過載上看，偏置比例導引律需要的過載較大，并且在導引末端所需過載急劇增加，使得在實際情況中由于過載的約束會對脫靶量和落角精度產生影響。因此在實際情況中CNG比BPNG有更好的魯棒性，并且更便于在被動尋的制導系統上實現。

7　致謝

本項目由兵科院預研基金（9140A01010313B Q01002）支持，同時也感謝審稿人在提高論文質量上提出的寶貴意見。

參考文獻

[1]Murtaugh S A,Criel H E.Fundamentals of proportional navigation[C].IEEE Spectrum.1969,3:75-85.

[2]Guelman M.Proportional navigation with a maneuvering target[C].IEEE Transactions on Aerospace and Electronic Systems.1972,8:364-371.

[3]Yuan P J,and Hsu S C.Solutions of generalized proportional navigation with maneuvering and non-maneuvering targets[C].IEEE Transactions on Aerospace and Electronic Systems.1995,31:469-474.

[4]Kim M,Grider,K V.Terminal guidance for impact attitude angle constrained flight trajectories[C].IEEE Transactions onAerospace and Electronic Systems.1973,9(6): 852-859.

[5]蔡洪,胡正東,曹淵.具有終端角度約束的導引律綜述[M].宇航學報.2010,31(2):315-323.

[6]Anchester I R,Savkin A V.Circular navigation guidance law for precision missile target engagements[M].Journal of Guidance.Control,and Dynamics.2006,29(2): 314-320.

[7]Manchester I R,Savkin A V.Circular navigation guidance law with incomplete information and uncertain autopilot model[M].Journal of Guidance,Control,and Dynamics.2004,27(8):1078-1083.

[8]Song T L,Shin J S,Han H S.Impact angle control for planar engagements[C].IEEE Transactions on Aerospace and Electronic Systems.1999,35(4):1439-1444.

[9]Kim B S,Lee G L,Han H S.Biased PNG law for impact with angular constraint[C].IEEE Transactions on Aerospace and Electronic Systems.1998,34(1):277-288.

[10] 李志平,郭建國,周軍.基于終端角度約束的滑模制導律設計[M].飛行力學,2012,30(4):345-348.

中圖分類號：TJ765.3

文獻標志碼：A

文章編號：2095-8110（2014）03-0011-07

收稿日期：2014–06–19；

修訂日期：2014–10–09。

基金項目：兵科院預研基金(9140A01010313BQ01002)

作者簡介：周魯（1990–），男，碩士，主要從事基于視覺信息的飛行器制導與控制系統設計。E-mail：47707550@qq.com

Research on Circular Navigation Guidance Law and Biased Proportional Navigation Guidannccee Law with Impact Angle Constraiinntt

ZHOU Lu，SONG Jian-mei，HUANG Lan
（Key Laboratory of Dynamics and Control of Flight Vehicle，Ministry of Education，School ofAerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

Abstract：In order to intercept against a target with a certain impact angle,we study two angle constraint guidance laws called circular navigation guidance(CNG)and biased proportional navigation guidance(BPNG).Firstly we establish the relative motion dynamic model and the gimbaled dynamic model.Then we explain the basic principles of the two guidance laws and use computer simulations to test three-dimensional intercepts against a moving or stationary target.We prove that the two guidance laws have been shown to give perfect results in miss distance and desired impact angle.Finally we present a comparative research of the two guidance laws on principle and simulation experiment.

Key words:Circular navigation guidance;Biased proportional navigation guidance;Impact angle constraint