基于頻響函數法的路面激勵下車輪軸頭力的估計

靳 暢，周 鋐，慕 樂

(同濟大學新能源汽車工程中心，上海 201804)

前言

近年來，對于動力總成系統(tǒng)振動噪聲的研究及優(yōu)化日趨成熟，動力總成對車內振動噪聲的貢獻得到了有效控制。這使得其它振動源所引起的車內振動噪聲顯得突出，其中路面激勵是重要的一方面。在粗糙路面激勵下，輪胎和車輪既會衰減路面激勵能量又能產生新的激勵，從而成為新的激勵源。路面通過接觸面對輪胎不斷進行局部壓縮和釋放，同時不斷地發(fā)生滾擠和釋放，共同形成包括垂向力Fz、側向力Fy、縱向力Fx、翻轉力矩Mx、牽引力矩My和回正力矩Mz的車輪軸頭六分力載荷，引起車內的振動和噪聲。測量軸頭載荷對車內振動噪聲的預測和控制具有重要的作用［1－2］。目前普遍采用車輪力傳感器獲取軸頭載荷信號，但是設備價格十分昂貴，安裝較復雜，需要輪輞適配等裝置。本文中嘗試采用基于頻響函數載荷識別方法，結合剛體動力學理論來間接估計軸頭力載荷。

1 基本理論

本文中闡述了頻響函數法估計車輪軸頭六分力的基本理論。提出頻響函數法識別車輪軸頭載荷，借助于剛體動力學的基本理論，采用附加剛體質量的方法推導出響應點到軸頭六分力的頻響函數，為實車工況下車輪軸頭載荷的估計提供理論依據。

1.1 頻響函數法載荷識別

國內外研究人員對頻響函數法識別載荷的研究已進行多年。文獻［3］中首先采用頻域法通過加速度響應識別了直升機主軸的動態(tài)載荷;文獻［4］中用動應變測量作為已知信息并使用頻域方法識別動載荷，建立了較系統(tǒng)的頻域識別方法;文獻［5］中指出測量響應的數目超過待識別載荷數目能夠在一定程度上減輕頻響函數病態(tài)和平滑濾掉噪聲產生的誤差;文獻［6］中研究了載荷位置未知情況下的載荷識別問題，采用的是頻響函數直接求逆法，在求逆過程中利用了奇異值分解技術;文獻［7］中用頻域方法識別直升機的動載荷;文獻［8］中將隨機振動的虛擬激勵法做了逆向推廣，用確定性方式求解了平穩(wěn)隨機振動的荷載譜識別問題;文獻［9］中提出改進的頻響函數矩陣求逆算法使頻響函數由長方陣改為簡單的方陣形式，再將計算出的激勵力求平均;文獻［10］中用逆虛擬激勵法識別隨機載荷譜并用試驗進行了驗證。

對于振動噪聲的研究，在車輪軸頭載荷估計中，可以將懸架系統(tǒng)視為多輸入多輸出的線性系統(tǒng)［11］，輸入f是車輪作用在軸頭的力載荷，輸出X是懸架側的振動響應，懸架系統(tǒng)的特性［H(ω)］是懸架側振動響應到軸頭載荷的頻率響應函數(FRF)。對于線性時不變的系統(tǒng)，如果輸入是隨機且部分相關的，那么系統(tǒng)的響應也是隨機且部分相關的。根據隨機振動理論［1］，輸入和輸出信號用功率譜密度表示，分別為［Gf(ω)］和［Gx(ω)］，響應的自功率譜密度矩陣可以表示為

式中H表示共軛裝置。若已知響應的自功率譜密度矩陣［Gx(ω)］和懸架系統(tǒng)的特性［H(ω)］，可以得到軸頭載荷［Gf(ω)］:

式中+表示頻響函數的偽逆矩陣。

1.2 剛體動力學

從式(2)可知，獲取軸頭力載荷的關鍵是對懸架系統(tǒng)頻響函數［H(ω)］的識別。本文中利用附加剛體質量的慣性參數推導頻響函數［12］。以直角慣性坐標系(oxyz)為運動參考系，其原點o與靜止剛體的原點相重合。剛體的微振動可用質心的3個移動 xc、yc、zc和繞參考軸的 3 個微轉動 θxc、θyc、θzc來描述。剛體上任一點 qi(x¨i，y¨i，z¨i)的運動加速度可以看作是剛體模態(tài)的疊加［13］，可表示為

式中:［qi］為i點運動加速度向量;［Ψi］為在小角度擾動下的剛體模態(tài)線性變換矩陣;［K］為模態(tài)向量參與向量。

設剛體模態(tài)以原點o的x、y、z3個方向的平動和繞x、y、z3個軸的轉動來描述，若將o點的剛體模態(tài)轉化為單位位移，則模態(tài)參與向量［K］就等同于o點在 x、y、z3個方向的平動和繞 x、y、z3 個軸的轉動，可表示為

式中:xci、yci和zci為 i點相對于 o 點的幾何坐標;x¨c、y¨c、z¨c、θ¨

xc、θ¨

yc、θ¨zc為剛體的運動加速度。

若已知模態(tài)參與向量［K］，就可以確定剛體上任一點的運動。為計算模態(tài)參與向量，至少需要6個運動加速度，因此應至少獲得剛體上2個點的運動加速度向量。為提高數值計算的精度，使運動加速度響應數大于模態(tài)參與向量的6個自由度，產生的增廣系統(tǒng)為

式(5)還可表示為

通過式(6)求得的模態(tài)參與向量［K］代表了剛體的全部運動特性。為減少測量信號產生的誤差，提高估計的準確度，引入一個計權矩陣［W］:

式中［W］為一個對角元素有0的單位陣，在計算模態(tài)參與向量［K］時，測量信號差的通道被剔除。

設模態(tài)參與向量［K］是由測得的剛體上的實際加速度響應［qm］乘以線性變換矩陣［Ψ］的偽逆矩陣得到:

將計算得到的模態(tài)參與向量帶入式(6)，剛體上每一點的平動計算如下:

若每通道測量的信號都很理想，則計算得到的剛體上的響應與測量的相一致。但由于實際信號測量存在誤差，為剔除測量信號差的通道，定義測量信號在頻域內的歸一化誤差:

在所關心的頻率內，每通道信號誤差的均值可定為

式中n為譜線數。平均誤差大的信號在模態(tài)參與向量的計算中應予以剔除:

運用以上剛體動力學理論，在車輪軸頭處安裝一個已知質量和轉動慣量的剛體質量塊，通過剛體的慣性參數推導出懸架側加速度響應到作用于軸頭與剛體質量安裝面中心軸頭力的頻響函數。

若有力作用在剛體質量上m點，該點的隨體坐標轉化為作用于原點的廣義力［14］為

式中:［FTa］為原點o的6自由度合力向量;［Fam］為作用在剛體上m點的力向量;［Ωm］為小角度擾動下作用力和原點合力的線性變換矩陣。

式(13)可寫成如下形式:

式中:Fxm、Fym和Fzm為作用在剛體上m點的分力;xcm、ycm和zcm為m點相對于o點的幾何坐標。

當有多個力作用在剛體上時，原點合力的估計為

將式(15)寫成:

作用在原點的合力FTa與作用在剛體質量上的軸頭六分力FR可推出剛體的運動方程:

式中:［M］為6×6的慣性參數矩陣;［A］為原點的加速度向量;［FTa］為外力在原點產生的合力;［FR］為作用在剛體質量上的軸頭六分力。

式(17)展開寫為:

式中:M 為剛體的質量;Ixx、Ixy、Ixz、Iyx、Iyy、Iyz、Izx、Izy和Izz為剛體的轉動慣量參數。

1.3 懸架響應點到軸頭力的頻響函數估計

根據式(12)，剛體質量原點的加速度向量可以表示為

式中［am］為剛體質量上的作用力產生的加速度響應向量。

剛體上的作用力和加速度響應的關系為

式中［Hm］為剛體質量上響應點到作用力的頻響函數矩陣。

式中［Hc］為6×6的頻響函數矩陣，剛體質量原點的加速度響應到軸頭六分力的頻響函數。

作用力到懸架側加速度響應的頻響函數［Has］可以通過測量得到:

式中［s］為懸架側的加速度響應。

將式(23)代入式(25)可以得到:

將式(24)代入式(26)，得到軸頭力與懸架側加速度響應的關系式:

式中［Hs］為懸架側加速度響應到軸頭六分力的頻響函數。

通過式(28)估計出懸架側加速度響應到作用于軸頭與剛體質量安裝面中心的軸頭力之間的頻響函數，再根據式(2)可以確定軸頭六分力:

式中:［Gs］為實際工況下懸架側加速度響應自功率譜密度;［Hs］為計算的懸架加速度響應到軸頭力的頻響函數;［Gf］為待估計的軸頭六分力的自功率譜密度。

2 試驗過程

2.1 頻響函數的測量

根據式(24)和式(28)，需要測量剛體質量塊上加速度響應到剛體質量塊上激勵的頻響函數以及懸架側響應點到剛體質量塊上激勵的頻響函數，以此計算懸架側加速度響應到軸頭六分力的頻響函數。采用錘擊法測量頻響函數，根據安裝、試驗要求以及剛體假設，設計一質量塊如圖1所示，質量塊應避免與軸頭及懸架上其他部件產生干涉，非對稱及偏心的設計有利于角加速度的測量。另外，水平和垂直面保證加速度計的安裝和其坐標位置的準確性。為確保質量塊的剛體性質，材料選用鋁，厚度為20mm，慣性參數矩陣為

通過試驗得到其第一階固有頻率為1 672Hz。由于路面激勵引起的車內振動噪聲頻率主要集中在150Hz以內［15］，所以設計的質量塊在所關心的頻率范圍內滿足剛體的假設。拆除試驗車輛右前輪，通過5個車輪安裝螺栓將質量塊緊固在轉子上如圖2所示。為保持頻響函數測量的自由邊界條件，采用如圖3所示的空氣彈簧支撐右前懸架。

根據式(5)，為了求得質量塊原點的加速度和角加速度，需要質量塊上至少有6個加速度響應，為提高計算精度，在質量塊上布置15個響應點，位置如圖4中M1～M5所示。為了得到懸架側的加速度響應，在懸架側5個點布置三向加速度計。根據式(15)可以計算出外力作用在原點處的合力，包括縱向力、側向力、垂向力、繞X的力矩、繞Y的力矩和繞Z的力矩6個分力，因此至少需要6個激勵點，為提高測量及數值計算精度，選擇14個激勵點，包括4個X向、5個Y向和5個Z向，均勻分布在質量塊上，位置如圖5所示。試驗采用錘擊法，使用橡膠錘頭保證中低頻的激勵能量。每個激勵點敲擊5次，進行平均，得到質量塊以及懸架側的頻響函數。

2.2 路面激勵工況的信號采集

測量實車在路面激勵工況下懸架側的加速度響應自功率譜密度。同時安裝Kistler S635應變式車輪力傳感器，測量軸頭六分力，以驗證頻響函數法估計軸頭載荷的有效性。試驗在試車場進行，選取比利時道路作為路面激勵，車速為40km/h。由于車輪力傳感器所定義的坐標原點O'與本文中所定義的坐標原點O在Y向(車輛橫向)不重合，如圖6所示，驗證六分力結果須進行坐標變換:

3 軸頭六分力的估計

3.1 誤差通道的剔除

若在2.1節(jié)中剛體質量上M1～M5測點頻響函數的測量都很理想，那么根據式(9)，計算得到的剛體質量加速度響應應與測量所得的相一致。但實際條件下會導致測量誤差的存在。表1列出了根據式(11)計算的質量塊上響應點的測量誤差，其中大于0.1(即誤差大于10%)的信號在后面的計算中通過計權矩陣［W］被剔除。

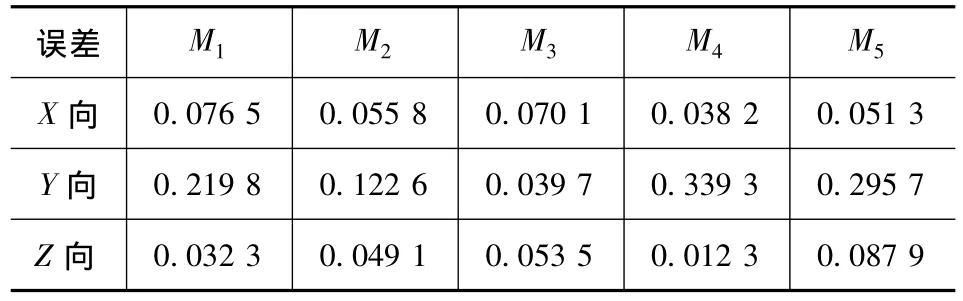
表1 質量塊上響應的平均測量誤差

3.2 頻響函數的計算

根據式(24)和式(28)并通過2.1節(jié)的試驗計算出懸架側加速度響應到車輪軸頭垂向力Fz、側向力Fy、縱向力Fx、翻轉力矩Mx、牽引力矩My和回正力矩Mz6個分力的頻響函數［Hs］。圖7和圖8為計算得到的懸架中3個響應點到軸頭縱向力Fx、牽引力矩My的頻響函數。

3.3 軸頭六分力的計算驗證

通過3.2節(jié)計算的懸架側加速度響應到軸頭六分力的頻響函數矩陣以及道路試驗得到的實車工況下懸架側加速度響應的自功率譜密度，根據式(29)估計出車輪軸頭六分力載荷，并與車輪力傳感器直接測量的軸頭力做了對比，如圖9～圖14所示。

計算結果中，側向力Fy、垂向力Fz和回正力矩Mz與實測值存在一定偏差，產生的原因如下:

(1)用頻響函數法進行載荷識別對于輸入輸出是基于線性關系的假設，在實際測量中，懸架系統(tǒng)存在一定的非線性導致識別產生誤差;

(2)實車道路試驗時懸架側加速度響應被重新布置，與測量頻響函數時的位置會有一些偏差，造成結果的偏差;

(3)在頻響函數測量過程中，由于空間限制，不能完全保證力錘每次激勵的位置與方向上的一致性，這會影響頻響函數測量的結果;

(4)在計算頻響函數［Hs］的逆時，對于非方陣只能求其廣義逆，會產生誤差，固有頻率附近頻響函數的病態(tài)和頻響函數的測量誤差，會出現數值計算的不穩(wěn)定性，當頻響函數矩陣階次較高時，常常由于矩陣的條件數較差造成病態(tài)，使誤差增大。

4 結論

闡述了頻響函數法估計車輪軸頭六分力的理論及試驗。提出頻響函數法識別車輪軸頭力載荷，采用附加剛體質量的方法推導出懸架響應點到軸頭六分力的頻響函數。設計了附加質量塊進行頻響函數的測量，并安裝車輪力傳感器在比利時道路進行實車工況懸架響應及軸頭力信號采集，驗證了所論述估計方法的有效性。發(fā)現部分估計結果有一定偏差，從頻響函數法識別載荷的假設前提、傳感器布置、頻響函數測量以及其求逆計算等方面闡述了可能導致偏差的原因，為進一步的研究提供了參考。

［1］ 龐劍，諶剛，何華．汽車噪聲與振動——理論與應用［M］．北京:北京理工大學出版社，2006．

［2］ 宋國民，崔硯宏．汽車虛擬測試系統(tǒng)的研究與發(fā)展［J］．世界汽車，2000(7):12－13．

［3］ Bartlett F D，Flannelly WG．Model Verification of Force Determination for Measuring Vibration Loads［J］．Journal of the American Helicopter Society，1979，24(4):10－18．

［4］ Hillary B，Ewin D J．The Use of Strain Gauges in Force Determination and Frequency Response Function Measurements［C］．Proceeding of the 2nd IMAC，Florida，USA，1984:627－634．

［5］ Stevens K K．Force Identification Problems-an Overview［C］．Proceedings of SEM Spring Conference on Experimental Mechanics，FL，USA，1987:838－844．

［6］ O’Callahan J，Piergentili F．Force Estimation Using Operational Data［C］．Proceedings of 8nd IMAC，1994，2768:1586 －1592．

［7］ 李萬新，張景繪．載荷確定方法和直升機六力素識別［R］．航空工業(yè)部飛行試驗中心科技報告，1884．

［8］ 林家浩，智浩，郭杏林．平穩(wěn)隨機振動載荷識別逆虛擬激勵法(一)［J］．計算力學學報，1998，15(2):127－136．

［9］ 田燕，王菁，鄭海起．多載荷識別頻響函數矩陣求逆的改進算法［J］．軍械工程學院學報，2002，14(4):13－17．

［10］ 李東升，郭杏林．隨機激勵下載荷譜識別［J］．大連理工大學學報，2003，45(5):561－566．

［11］ Park Joonhyung，Gu Perry．Operational Spindle Load Estimation Methodology for Road NVH Applications［C］．SAE Paper 2001－01－1606．

［12］ Park Joonhyung，Gu Perry．A New Experimental Methodology to Estimate Chassis Force Transmissibility and Applications to Road NVH Improvement［C］．SAE Paper 2003 －01 －1711．

［13］ Li Shumin，William Flagung，David Brown．Indirect Measurement of Rotation/Moments Impedance Functions［C］．SAE Paper 951271．

［14］ Declercq SM，Lazor D R，Brown D L．A Smart 6-DOFLoad Cell Development［C］．Proceedings of IMAC-XX:A Conference on Structural Dynamics，Vol．4753 I:844-853．

［15］ Bryan M E．A Tentative Criterion for Acceptable Noise Levels in Passenger Vehicles［J］．Journal of Sound and Vibration，1976，48(4):525－535．