輪轂驅動電動汽車垂向特性與電機振動分析

童 煒，侯之超

(清華大學，汽車安全與節能國家重點實驗室，北京 100084)

前言

隨著電動汽車的興起，輪轂電機驅動模式以其獨特的優勢成為當前的一個研究熱點。輪轂電機驅動因為省去變速器、傳動軸和差速器等傳動系統，使得傳動鏈縮短、效率增高、結構更緊湊。電機的位置與性能也使ABS、TCS和ESC等功能更易于實現［1］。

盡管輪轂電機驅動有諸多優勢，但應用于實際工程仍存在很多挑戰。首先，輪轂電機增加了車輛非簧載質量，惡化了車輛行駛的平順性［2］;其次，因直接或經過減速機構與車輪固連，電機易受路面激勵而產生較大振動，導致其機械部分的工作壽命縮短，加劇了定子與轉子間的磁隙波動;第三，因省去傳統內燃機車輛的傳動系統，電機轉矩波動直接作用于車輪，可能引起懸架前后方向共振以及整個驅動系統的振動。

文獻［3］中介紹了一種改進方案，創新設計用于輪轂驅動的盤式電機，將定子轉變為簧載質量，轉子通過長半軸驅動車輪，明顯改善了車輛的垂向性能。但電機轉子和定子會因來自路面或車身的沖擊而錯位，引起電機磁場變化，加劇電機轉矩波動。文獻［4］中對比分析了車輛被動懸架與主動懸架對車輛乘坐舒適性和安全性的影響，以結合電機轉矩特性選擇合適的懸架系統。文獻［2］中從汽車垂向性能和振動傳遞途徑等角度綜述了國內外抑制垂向振動影響的策略及其局限性。日本普利斯通公司開發的動態吸振型輪轂驅動系統［5］將電機懸置，電機既作為動力源又充當質量吸振器，能在較寬轉速范圍內提高車輛的平順性和安全性。文獻［6］和文獻［7］中對利用吸振器原理設計吸振機構或引入電機懸置以改善車輛垂向特性進行了探討。

本文中基于1/4輪轂驅動車輛模型，定義了車輛平順性和電機垂向振動的評價指標;并以某微型電動汽車為對象，分析了車身偏頻、懸架阻尼比、輪胎垂向剛度與懸架剛度比、車輛簧載質量與車輪系統質量比、電機系統與車輪系統質量比等關鍵設計參數對車輛及電機振動的影響，提出了相關參數選擇的建議。

1 動力學模型及性能指標

1.1 動力學模型

考慮車輛垂向振動，采用1/4車輛簡化模型，見圖1。

圖中:m1為除輪轂電機系統外的非簧載質量，即車輪系統質量(輪胎、車輪和制動片等);m2為車輛簧載質量;m3為輪轂電機系統質量(對于間接驅動，則含行星齒輪減速機構的質量);x0為路面不平度，x1和 x2分別為車輪和車身的垂向位移。

其車輛垂向振動方程為

式中:k1、c1分別為輪胎垂向剛度和阻尼(近似為零);k2、c2分別為懸架剛度和阻尼。

1.2 性能指標

選取車輪相對動載荷、電機垂向振動加速度、懸架動撓度和車身垂向振動加速度作為評價車輛和電機垂向振動特性的指標。對式(1)和式(2)作傅里葉變換，可得到各指標的幅頻特性。為反映路面影響，以路面速度x·0為參照，分別定義各指標相對值如下。

車輪靜載荷為G=(m1+m2+m3)g。按照汽車理論［8］約定，車輪動載荷為Fr=k1(x1－x0)+c1(x·1－x·0)。考慮路面輸入，車輪相對動載荷的幅頻特性可表示為

常規輪轂電機驅動，電機與車輪直接相連。電機垂向加速度的相對幅頻特性為

同理，懸架動撓度相對幅頻特性為

而車身垂向加速度的相對幅頻特性為

以上諸式中，

其中:γ=k1/k2為輪胎垂向剛度與懸架剛度比;ξ=為懸架阻尼比;λ=ω/ω0為路面激勵與車身圓頻率比簧載質量與非簧載質量比定義為μ=m2/(m1+m3)=μ21/(1+μ31)，其中，μ21=m2/m1，μ31=m3/m1，分別為簧載質量與車輪系統質量比、電機系統與車輪系統質量比;‘^’表示拉普拉斯變換，‘˙’表示速度，‘˙˙’表示加速度。

路面激勵下，對應上述各項指標的均方根響應［8］可表示為

式中:n0為參考空間頻率;Gq(n0)為路面不平度系數;u與f分別為車輛行駛速度與頻率。

值得注意的是，均方根響應僅反映各項指標在分析頻段內的平均值。結合均方根響應與相對幅頻特性，可更全面地對系統垂向振動特性進行評價。

2 參數影響分析

針對某微型輪轂驅動汽車［6］，首先分析車輛不同參數匹配組合下各指標對應的均方根響應，然后單獨分析主要參數 f0(=ω0/2π)、ξ、γ、μ21和 μ31對各指標幅頻特性的影響。

2.1 參數選取

對于乘用車，車輛偏頻f0常取0.8～1.6Hz，阻尼比取0.2～0.4［9］。各變量初值及其取值范圍見表 1。換算后得到車輛具體參數 m1、m2、m3、k1、k2和c2的取值，如表2所示。

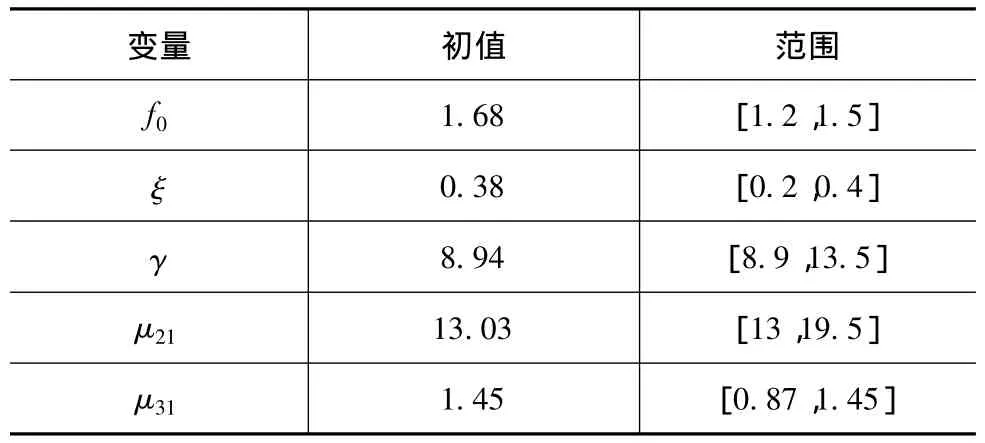
表1 變量初值及取值范圍

表2 車輛具體參數取值范圍

2.2 均方根響應分析

選取 B 級路面［8］，Gq(n0)=64 ×10－6，n0=0.1，并假設車速為10m/s，計算各指標對應的均方根響應，由此分析車輛具體參數組合的影響。

圖2為m2與k2匹配的影響，圖中曲面表示均方根值的三維視圖，底部平面曲線為其等高線。

圖3～圖6分別為c2與k2、k1與k2、m2與m1和m3與m1各組合匹配的影響。

由圖2可知，m2和k2對車輪動載荷、電機垂向振動加速度和車身振動加速度影響趨勢一致，即m2越大、k2越小，三指標對應均方根響應越小，此時對應車身偏頻也最小;但懸架動撓度會增大。

由圖3可知，c2和k2組合對車輪動載荷、電機垂向振動加速度和懸架動撓度3個指標影響趨勢一致，即增大c2利于減小均方根值;但車身振動加速度增大。

由圖4可知，降低k1和增大k2有利于減小車輪動載荷、電機垂向振動加速度和車身振動加速度響應均方根值。

由圖5可知，m2和m1的匹配關系對車輪動載

荷、懸架動撓度和車身振動加速度的影響情況與對應電機垂向振動加速度的相反，即增大m1和減小m2有利于降低電機振動，但會惡化其他性能。

由圖6可知，增加電機系統質量有利于降低電機振動但會惡化其他性能，這與減小非簧載質量以獲得較好乘坐舒適性和安全性相反。

2.3 相對幅頻特性分析

計算顯示，各參數對車身振動加速度、懸架動撓度和車輪相對動載荷幅頻特性影響趨勢與文獻［8］中所述一致，即減小車身偏頻f0、增大懸架阻尼比ξ、減小輪胎與懸架垂向剛度比γ、增大簧載質量與車輪系統質量比μ21=m2/m1，以及減小電機系統與車輪系統質量比μ31=m3/m1，有利于降低車身加速度、車輪相對動載荷及懸架動撓度響應高頻共振峰;減小f0甚至會降低全頻域內的幅值。下面將重點分析各變量對電機垂向振動加速度的影響(為便于分析影響趨勢，加大了部分變量取值范圍)，結果見圖7。

由圖7可知，電機共振頻帶在10～15Hz內，且共振峰值很大;隨著f0和γ減小，電機垂向振動加速度的幅頻特性共振峰向低頻移動，同時幅值降低;增大ξ共振峰幅值減低，共振峰幾乎不移動。值得注意的是，μ21和μ31對電機垂向振動加速度與其他性能的影響情況恰好相反:即減小μ21和增大μ31有利于降低電機振動而惡化其他性能，這點與響應均方根分析結論吻合。

綜上所述，響應均方根分析用于整體評估，頻域分析主要用于分析各指標性能的幅頻特性，能直觀了解性能惡化的局部頻帶。因此，匹配車輛各參數應根據各性能指標設計要求的側重點而合理選取分析方法，須特別注意電機振動的影響。以外轉子型輪轂電機為例，定子與轉向節固連，外轉子與輪輞通過螺栓連接。電機振動過大，不僅加速連接件損壞，且定子與轉子間振動波動會引起磁隙變化，進而影響電機輸出轉矩的平穩性。

3 結論

(1)依據1/4車輛垂向動力學模型，給出了包含車輪相對動載荷、輪轂電機垂向振動加速度、懸架動撓度及車身垂向振動加速度等用于評價車輛平順性和電機垂向振動的指標。

(2)分析了車輛具體參數 m1、m2、m3、k1、k2和c2的不同組合對各性能均方根響應的影響，并推薦了參數的選取區域。

(3)分析了車身偏頻f0、懸架阻尼比ξ、輪胎與懸架剛度比γ、簧載與車輪系統質量比μ21、電機系統與車輪系統質量比μ31對各指標的幅頻特性影響。其中減小μ21和增大μ31有利于降低電機振動，但會惡化其他性能。

［1］ Murata S．Vehicle Dynamics Innovation with In-Wheel Motor［C］．SAE Paper 2011－39－7204．

［2］ 寧國寶，萬鋼．輪邊驅動系統對車輛垂向性能影響的研究現狀［J］．汽車技術，2007(3):21 －25．

［3］ Hredzak B，Gair S，Eastham JF．Control of an EV Drive with Reduced Unsprung Mass［J］．IEEE Transactions on Electric Power Applications，1998，145(6):600 －606．

［4］ Rojas R A E，Niederkofler H，Willberger J．Comfort and Safety Enhancement of Passenger Vehicles with In-Wheel Motors［C］．SAE Paper 2010－01－1146．

［5］ Nagaya G，Wakao Y，Abe A．Development of an In-wheel Drive with Advanced Dynamic-damper Mechanism［J］．JSAE Review，2003，24(4):477 －481．

［6］ 梁銳，余卓平，寧國寶．基于吸振原理的輪邊驅動電動車垂向振動負效應的抑制［J］．機械設計，2008，25(1):28 －30．

［7］ 趙艷娥，張建武，韓旭．輪轂電機獨立驅動電動汽車動力減振機構設計與研究［J］．機械科學與技術，2008，27(3):395－398，404．

［8］ 余志生．汽車理論［M］．北京:機械工業出版社，2007．

［9］ 劉維信．汽車設計［M］．北京:清華大學出版社，2001．