一種基于多重分形特性檢測(cè)海面弱目標(biāo)的新方法
張 波 張丹婷 胡 沖
(1.西安市導(dǎo)航技術(shù)研究所,陜西 西安 710068;2.西安電子科技大學(xué) 雷達(dá)信號(hào)處理國(guó)防科技重點(diǎn)實(shí)驗(yàn)室,陜西 西安 710071)
0 引言
海雜波是雷達(dá)發(fā)射脈沖照射的局部海面的后向散射回波。對(duì)海雜波進(jìn)行特性分析和建模仿真對(duì)于設(shè)計(jì)有效的雷達(dá)檢測(cè)方案和評(píng)價(jià)雷達(dá)檢測(cè)性能至關(guān)重要。傳統(tǒng)的研究主要是研究其統(tǒng)計(jì)特性,建立統(tǒng)計(jì)分布模型,如典型的瑞利(Rayleigh)分布、對(duì)數(shù)正態(tài)(Log-normal)分布、韋布爾(Weibull)分布和K分布等[1]。然而,這些模型把海雜波視為某一隨機(jī)過(guò)程的樣本函數(shù),這在很大程度上并非因?yàn)楹ks波的物理本質(zhì),而是出于其看似隨機(jī)的波形。實(shí)際上,高分辨率雷達(dá)在低掠射角情況下測(cè)量的海雜波往往不具有高斯分布特性,海雜波并不是平穩(wěn)的,而是呈現(xiàn)為非線性的不平穩(wěn)性[2-4]。這樣經(jīng)典雷達(dá)目標(biāo)檢測(cè)所作的獨(dú)立、線性,平穩(wěn)等假設(shè)均不符合真實(shí)情況,基于這些假設(shè)而采用的經(jīng)典雷達(dá)目標(biāo)最佳檢測(cè)策略不可避免導(dǎo)致檢測(cè)性能下降。
分形理論[5]的發(fā)展不僅為數(shù)學(xué)和物理提供了全新的觀察視角和觀察深度,也為雜波建模和分析提供了新的動(dòng)力和方向:S.Haykin等人[6-7]對(duì)海雜波的研究表明,海雜波存在分?jǐn)?shù)維的混沌吸引子,且存在大于零的Lyapunov指數(shù),進(jìn)而表明,用非線性學(xué)科中的混沌與分形方法研究雜波模型比傳統(tǒng)的隨機(jī)方法更為有效。
已有很多學(xué)者對(duì)海雜波的分形特性進(jìn)行過(guò)不同方面的研究,也取得了不少成果[8-9]。本文從實(shí)測(cè)海雜波數(shù)據(jù)入手,首先計(jì)算了海雜波的盒維數(shù),又通過(guò)分析海雜波的統(tǒng)計(jì)特性,發(fā)現(xiàn)其偏離高斯分布并具有長(zhǎng)時(shí)相關(guān)性,且在較大的范圍內(nèi)具有尺度不變性,因此,利用多重分形模型可以較好的刻畫海雜波的復(fù)雜特性。本文從時(shí)間和空間上綜合考慮,利用雜波與含目標(biāo)單元多重分形譜的差別,提出一種新的檢測(cè)方法。對(duì)實(shí)測(cè)數(shù)據(jù)的分析表明該方法是有效的,并且具有較小的計(jì)算量,為海雜波背景下的目標(biāo)檢測(cè)提供了一條新的思路和有效手段。
1 分形維數(shù)(盒維數(shù))
分形是一類復(fù)雜性頗高的、沒(méi)有特征長(zhǎng)度,但具有一定意義下的自相似的圖形和結(jié)構(gòu)的總稱[10]。分形維數(shù)是分形對(duì)象的復(fù)雜度和不規(guī)則度的定量描述,分形維數(shù)是分形的極其重要的特征數(shù),是刻畫分形的不變量。當(dāng)海面上存在艦船目標(biāo)時(shí),會(huì)改變?cè)搮^(qū)域海面的運(yùn)動(dòng)狀態(tài),將在雷達(dá)回波信號(hào)的分?jǐn)?shù)維差異中體現(xiàn)出來(lái)。
對(duì)于分形維數(shù)有很多不同的定義,最好的理論定義是Hausdorf維。但由于Hausdorf維數(shù)計(jì)算復(fù)雜,實(shí)際中一般用其他定義來(lái)計(jì)算分形維數(shù)。在求解分形維數(shù)的方法中,盒維數(shù)是應(yīng)用最廣泛的維數(shù)之一。盒維數(shù)的計(jì)算方法如下[11]:
(1)選擇一個(gè)一定長(zhǎng)度的曲線F將其長(zhǎng)度與幅度歸一化后放入一正方形內(nèi)。
(2)選取邊長(zhǎng)為εm(m=1,2,…,M)的方格網(wǎng)(盒子)去覆蓋單位正方形,計(jì)算不同尺寸εm下與F交疊的盒子個(gè)數(shù)Nm(ε)。當(dāng)εm→0時(shí),則盒子恰好包含F(xiàn)的一個(gè)點(diǎn),亦可認(rèn)為此時(shí)盒子與點(diǎn)的形狀完全符合,正好填滿F。
(3)定義盒維數(shù) Db=lgNm(ε)/(-lgεm)。 分?jǐn)?shù)維是盒維數(shù)在 εm→0 時(shí)的極限值。實(shí)際中盒子尺寸不可能無(wú)窮小,但只要小到一定程度后,結(jié)果差距相當(dāng)微弱,就可以用盒維數(shù)來(lái)取代分?jǐn)?shù)維作為分析的對(duì)象.
(4)如果曲線是一種完全的分形,則對(duì)數(shù)比曲線Db=lgNm(ε)/(-lgεm)為一直線,盒維數(shù)Db就是該直線的斜率,如果對(duì)數(shù)比曲線不是理想直線,說(shuō)明該圖形分形特征不明顯,則用對(duì)數(shù)比曲線的最小方差擬合直線的斜率來(lái)代替。同時(shí),Mandelbrot有效維數(shù)的概念也說(shuō)明分形特征是有尺寸范圍的。所以實(shí)際處理盒維數(shù)時(shí),應(yīng)該從對(duì)數(shù)比值趨于穩(wěn)定,對(duì)數(shù)比曲線趨于直線的范圍內(nèi)開(kāi)始擬合。
本文使用的實(shí)測(cè)海雜波數(shù)據(jù)為本研究所采用的海雜波數(shù)據(jù)是某S波段雷達(dá)于2010年5月在某海灣采集到的,該雷達(dá)架設(shè)在海拔500m的山上,臨海。雷達(dá)的主要參數(shù)如下:
線性調(diào)頻信號(hào),中頻30MHz,帶寬5MHz,采樣頻率40MHz,脈寬46μs,錐形波束寬度 1.0°,天線固定不轉(zhuǎn),入射余角 1.0°。
圖1為某一段長(zhǎng)度為100的海雜波經(jīng)歸一化后,εm=0.10時(shí)的覆蓋情況,圖2為最小二乘擬合的情況,經(jīng)計(jì)算得Db=1.4756。當(dāng)數(shù)據(jù)長(zhǎng)度數(shù)增加時(shí),盒子越小越精確。
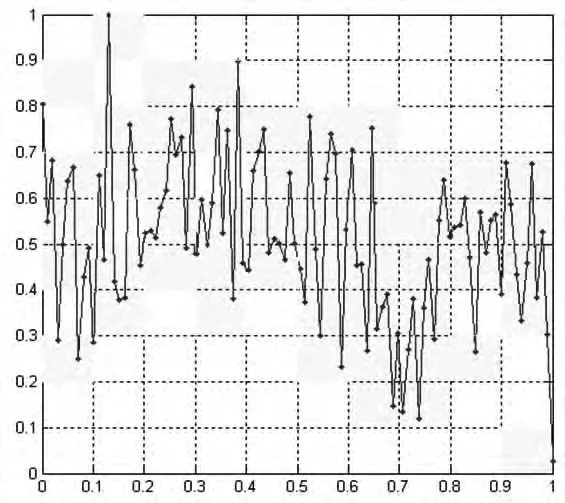
圖1 盒維數(shù)法圖示

圖2 lgNm(ε)/(-lgεm)
表1給出了實(shí)測(cè)海雜波數(shù)據(jù)與目標(biāo)數(shù)據(jù)在不同時(shí)刻的盒維數(shù)計(jì)算結(jié)果。由表1可看出含目標(biāo)時(shí)的海雜波的盒維數(shù)明顯大于不含雜波的情況。但在高海態(tài)等情況下,海雜波和目標(biāo)回波的分維值的平均值相差較小,而從整體上看兩者的分維值交疊在一起,僅用其進(jìn)行檢測(cè)是不可靠的[12]。

表1 海雜波的分形維數(shù)
2 多重分形的判定及譜函數(shù)的計(jì)算
分形盒維數(shù)能反映分形信號(hào)的幾何特征信息,對(duì)信號(hào)的復(fù)雜度、和全局性進(jìn)行定量的描述。但計(jì)盒維數(shù)法計(jì)算認(rèn)為只要盒子內(nèi)有圖形的像素這個(gè)盒子就被計(jì)進(jìn)來(lái),而不考慮盒子內(nèi)像素的多少,這樣得到的分維必然失去很多信息,這便是單一分形不夠細(xì)致之處;而多重分形考慮盒子內(nèi)像素或者其他物理量的差別,歸一化之后得到一個(gè)概率分布的集,再用一個(gè)多重分形譜進(jìn)行描述,得到的結(jié)果包含了許多被單一分形忽略的信息。
在計(jì)算海雜波的多重分形特性之前,首先應(yīng)判斷其偏離高斯分布并具有長(zhǎng)時(shí)相關(guān)性,且在較大的范圍內(nèi)具有尺度不變性[13]。
為了檢驗(yàn)海雜波是否具有非高斯特性,計(jì)算其偏度系數(shù)Cs和峰度系數(shù)Ck:

其中μk=E(X-EX)k,k=2,3,4。偏度系數(shù)刻畫分布函數(shù)的對(duì)稱性,鋒度系數(shù)刻畫不同類型分布的集中和分散的程度。對(duì)于正態(tài)分布來(lái)說(shuō),Cs=0,Ck=3。 經(jīng)計(jì)算,本文采用的實(shí)測(cè)雜波數(shù)據(jù),其 Cs>0,Ck>3,與高斯分布有一定差距,因此海雜波數(shù)據(jù)具有非高斯特性。
下面采用對(duì)數(shù)方差—時(shí)間圖法[14]分析海雜波的長(zhǎng)時(shí)相關(guān)性。圖3中作出了對(duì)數(shù)方差—時(shí)間曲線,如果海雜波數(shù)據(jù)的對(duì)數(shù)方差—時(shí)間曲線斜率大于-1,則具有長(zhǎng)時(shí)相關(guān)性。有圖顯然可以得到肯定的結(jié)論。

圖3 海雜波的對(duì)數(shù)方差—時(shí)間曲線


如果上式在一定的m區(qū)間內(nèi)成立,則序列具有分形特性。此外,如果質(zhì)量指數(shù)τ(q)不是q的線性函數(shù),那么稱被觀察序列在這一區(qū)間存在多重分形特性;否則,就為單一分形[15]。利用上述方法對(duì)一段實(shí)測(cè)海雜波進(jìn)行分析,結(jié)果如圖4所示。圖4給出了不同q值下的log2(m)~log2(Sm(q))曲線,可以看出式(4)在較大范圍內(nèi)均成立,這表明海雜波具有多重分形特性。
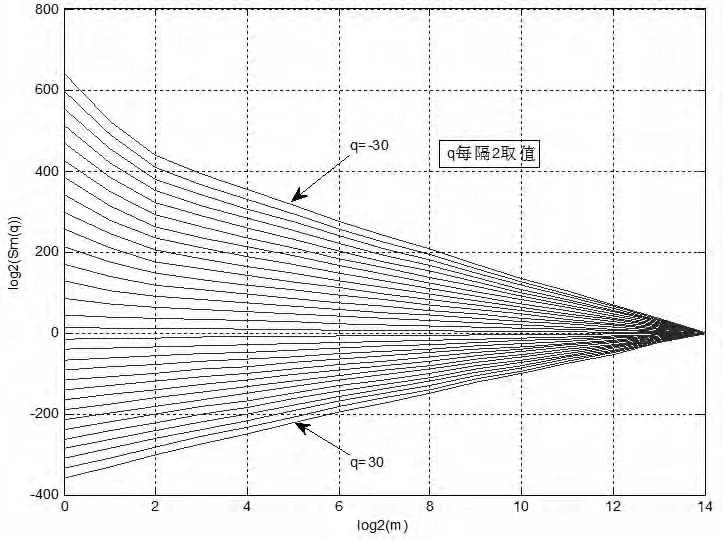
圖4 海雜波的log2(m)~log2(Sm(q))曲線
下面給出多重分形譜的計(jì)算方法。在式(4)的線性區(qū)間內(nèi),利用最小二乘法求解下式得到:
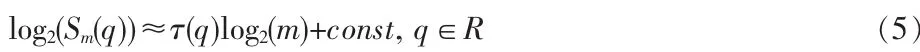
對(duì) q~τ(q)進(jìn)行如式(6)、(7)所示的 Legendre 變換即可得到多重分形譜。

式中:τ(q)為標(biāo)度指數(shù);f(α(q))即為多重分形譜函數(shù)。
由圖5以看到質(zhì)量指數(shù)τ(q)不是q的線性函數(shù),圖中有一個(gè)明顯的折點(diǎn)。圖6給出了標(biāo)度指數(shù)α(q)隨q變化情況,可以看到在零附近有一次驟降。
綜上,根據(jù)上文中提到的判定準(zhǔn)則,認(rèn)為本批數(shù)據(jù)是多重分形的,多重分形譜如圖7所示,并且其在其在q=0處取得最大值1。
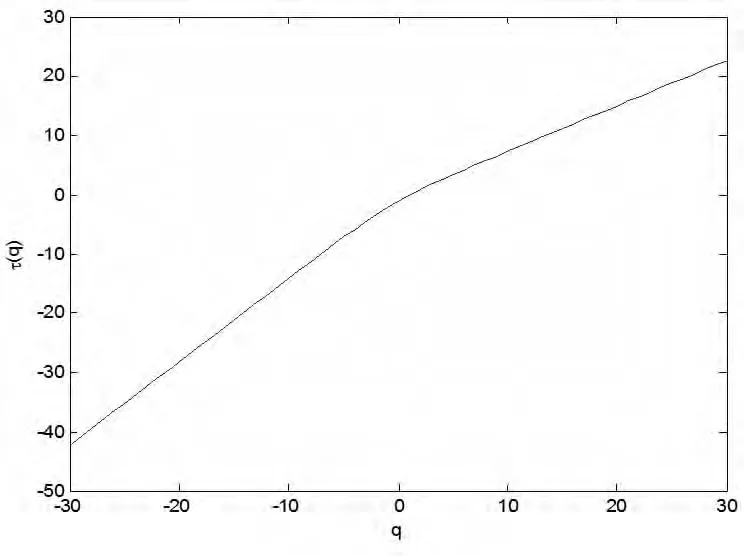
圖5 q~τ(q)曲線

圖6 q~α(q)曲線
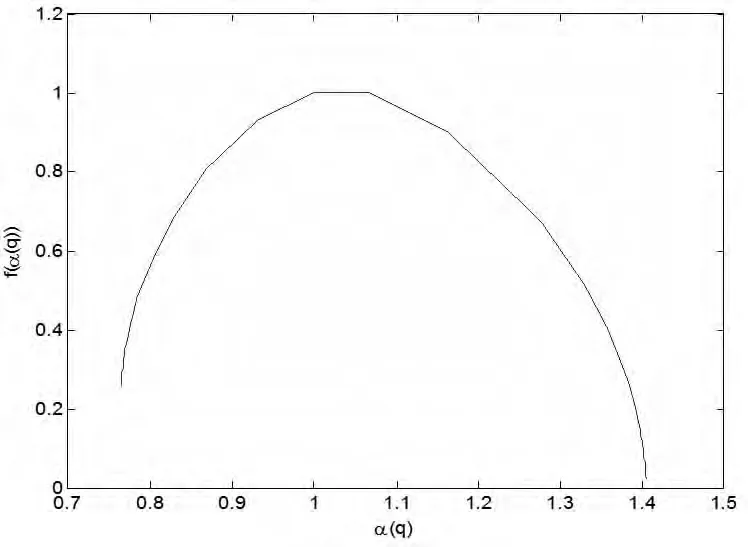
圖7 海雜波的多重分形譜函數(shù)
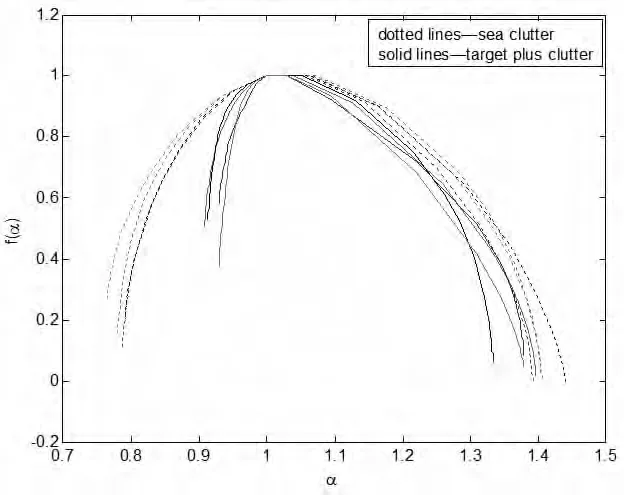
圖8 多重分形譜對(duì)比
圖8分別給出了含目標(biāo)與不含目標(biāo)的距離單元在不同時(shí)刻的多重分形譜。從該圖可以看到,海雜波數(shù)據(jù)在存在目標(biāo)時(shí),譜寬變窄,而多重分形譜寬的大小反映了整個(gè)分形結(jié)構(gòu)上概率測(cè)度分布不均勻性的程度和過(guò)程的復(fù)雜性,譜寬越寬,譜的結(jié)構(gòu)越豐富,過(guò)程相對(duì)越復(fù)雜,這表明海雜波比目標(biāo)復(fù)雜。這一差別在譜的左邊尤其明顯,這表明α較小(大概率)的部分差別更大。而目標(biāo)與目標(biāo)、雜波與雜波在不同時(shí)刻的差別較小,這表明多重分形譜較為穩(wěn)定,適合用于檢測(cè)。
為了利用這種差別來(lái)判別海面某一區(qū)域是否出現(xiàn)目標(biāo),我們計(jì)算f(α)對(duì)α的積分,表2列出了積分的結(jié)果。從表2可看出含目標(biāo)的距離單元相應(yīng)的積分結(jié)果明顯小于不含目標(biāo)的情況,這與圖8一致。如果設(shè)定合適的門限,則可根據(jù)積分值判斷目標(biāo)的出現(xiàn),而且文獻(xiàn)[6]表明在數(shù)據(jù)長(zhǎng)度達(dá)到2000點(diǎn)時(shí),分形估計(jì)就趨于穩(wěn)定,因而使用分形方法進(jìn)行的檢測(cè)計(jì)算量小于傳統(tǒng)的基于統(tǒng)計(jì)建模的方法,時(shí)效性也更好。圖9為檢測(cè)方案。

表2
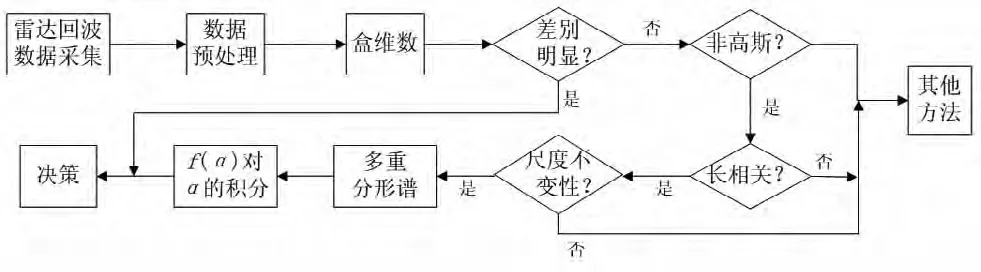
圖9 檢測(cè)方案圖
3 結(jié)束語(yǔ)
本文分析計(jì)算了海雜波的分形維數(shù)及多重分形特性。由本文的分析,可以看出實(shí)測(cè)的海雜波序列具有多重分形特性,利用多重分形譜可以較好的描述復(fù)雜不規(guī)則的海雜波序列。在此基礎(chǔ)上,利用雜波包含與不包含目標(biāo)時(shí)多重分形譜的差別,提供了一種檢測(cè)海上目標(biāo)的新方法,該方法具有計(jì)算量小的優(yōu)點(diǎn)。由于本文所用的數(shù)據(jù)有限,還有待于利用更多數(shù)據(jù)進(jìn)一步詳細(xì)地評(píng)估該方法。
[1]H C.Chan.Radar sea-clutter at low grazing angles[J].IEE Proceedings,1990,137:102-112.
[2]S.Haykin,R.Bakker,B W.Currie.Uncovering nonlinear dynamics-the case study of sea clutter[J].IEEE Proceedings,2002,90:860-881.
[3]S C.Guedes,Z.Cherneva,E.M.Antao.Steepness and asymmetry of the largest waves in storm sea states[J].Ocean Engineering,2004,31:1147-1167.
[4]E.Conte,A D.Maio.Mitigation techniques for non-Gaussian sea clutter[J].O-ceanic Engineering,2004,29:284-302.
[5]B.B.Mandelbrot,W.H.Freeman.The Fractal Geometry of Nature[J].W.H.Freeman,San Francisco,CA,1982.
[6]T.Lo,H.Leung,J.Litva and S.Haykin.Fractal characteristics of sea scattered signals and detection of sea-surface targets[J].IEE Proceedings,1993,140:243-50.
[7]S.Haykin,S.Puthusserypady.Chaotic dynamics of sea clutter[J].Chaos,1997,7:777-802.
[8]F.Berizzi,E.Dalle-Mese.Fractal analysis of the signal scattered from the sea surface[J].Antennas Propagation,1999,7:324-338.
[9]J.Chen,K Y.Lo,H.Leung and J.Litva.The use of fractals for modeling EM waves scattering from rough sea surface[J].Geoscience and Remote Sensing,1996,34:966-972.
[10]英林,謝勝利,等.信號(hào)處理新方法導(dǎo)論[M].北京:清華大學(xué)出版社,2004.
[11]W D.Hu,W X.Yu,A.Luo.Fractal detection of radar weak targets[J].IEEE Proceedings,1995,1:140-144.
[12]杜干,張守宏.分形模型在海上雷達(dá)目標(biāo)檢測(cè)中的應(yīng)用[J].電波科學(xué)學(xué)報(bào),1998,13:377-381.
[13]石志廣,周劍雄,付強(qiáng).基于多重分形模型的海雜波特性分析與仿真[J].系統(tǒng)仿真學(xué)報(bào),2006,18:2289-2292.
[14]W.Leland,M.Taqqu,W.Willinger and D.Wilson.On the self-similar nature of Ethernet traffic(extended version)[J].IEEE/ACM Transactions on Networking,1994,2:1-15.
[15]J.Hu,W W.Tung,J B.Gao.Detection of Low Observable Targets Within Sea Clutter by Structure Function Based Multifractal Analysis[J].IEEE Transactions,2006,54:136-143.

