利用非線性規(guī)劃方法最優(yōu)化灰色預測模型

陳友軍，何洪英，魏 勇

CHEN Youjun,HE Hongying,WEI Yong

西華師范大學 數(shù)學與信息學院，四川 南充 637009

College of Mathematics and Information,China West Normal University,Nanchong,Sichuan 637009,China

1 引言

鄧聚龍教授20世紀70年代末、80年代初提出灰色系統(tǒng)理論[1]以來，該理論已廣泛地應用于石油、地質、醫(yī)學、工業(yè)控制、管理、農業(yè)等眾多領域；作為該理論核心之一的灰色GM（1，1）預測模型，它建立在研究少數(shù)據(jù)、貧信息的不確定性問題基礎上，已在各方面顯示出它比很多其他預測方法更具優(yōu)越性。傳統(tǒng)的GM（1，1）模型參數(shù)辨識方法[1-2]和其他一些參數(shù)辨識新方法[3-9]，如灰色相對關聯(lián)度方法、折扣最小一乘法、目標規(guī)劃法、線性規(guī)劃法等在建模的過程中都用ε(k)=x(0)(k)-(-az(1)(k)+b)作為實際值與模擬值的殘差來建模。然而在評價模型優(yōu)劣時都采用實際值與依據(jù)白化微分方程解的還原值x^(0)(k)的相對誤差或者絕對誤差平方和來判斷的，所以建模方法與評價標準存在一定差異，即并不是所有的模型都滿足只要殘差平方和最小則其模擬精度最高，這就為進一步優(yōu)化模型留下了空間。

從文獻[1-2]可知，在檢驗一個GM（1，1）模型的模擬精度時，一般采用

計算得到模擬精度，其中 ε(avg)指 GM（1，1）模型的平均相對誤差，且

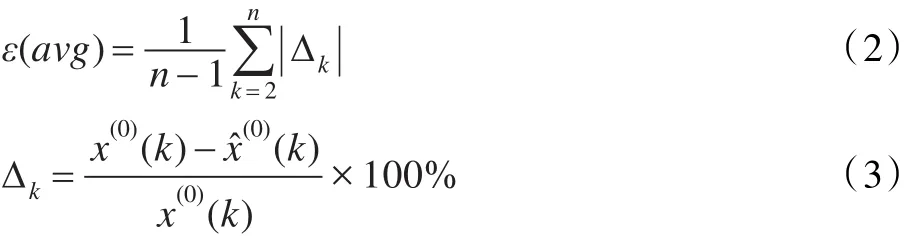
而模型的模擬值指通過GM（1，1）模型的時間響應序列[1-2]計算得到的還原值序列[1-2]，只是針對 GM（1，1）模型白化微分方程的初值選擇方法不同，其時間響應式的計算方法也略有差異[3-9]。

很明顯，要使GM（1，1）模型取得最大的模擬精度，則式（2）應當取得最小值，即GM（1，1）模型的平均相對誤差應當取得最小值。本文就通過直接建立一個非線性規(guī)劃模型，目標是使式（2）取得最小值，使用數(shù)學軟件LINGO 11.0，可以直接求解得到這個模型的全局最優(yōu)解[10]。通過大量的數(shù)據(jù)分析發(fā)現(xiàn)，采用這種方法建立的最優(yōu)化GM（1，1）模型的模擬精度及預測精度都有了相當大的提高，并且新模型具有白指數(shù)重合律。

2 最優(yōu)化GM（1，1）模型的建立

2.1 灰色GM（1，1）模型

定理1[1-2]設為非負原始數(shù)據(jù)序列，為X(0)的1-AGO序列，其中；灰色模型 x(0)(k)+az(1)(k)=b的背景值序列為Z(1)={z(1)(2),z(1)(3),…,z(1)(n)}，則

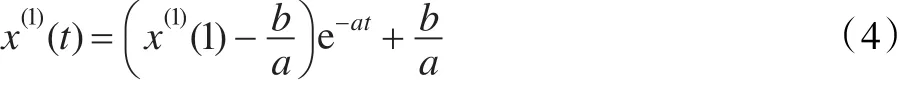
（2）GM（1，1）模型 x(0)(k)+az(1)(k)=b的時間響應序列為：

（3）還原值

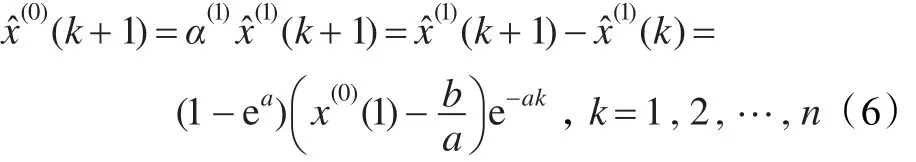
在上述GM（1，1）模型中，參數(shù)a為發(fā)展系數(shù)，b為灰作用量。

2.2 平均相對誤差最小的非線性規(guī)劃模型

針對GM（1，1）模型檢驗的一般方法，即一般使用最終模型的模擬值序列與原始數(shù)據(jù)序列間的平均相對誤差的大小來評價GM（1，1）模型的好壞，最終模型的模擬值序列可以由上面的式（6）得到，故可以建立一個平均相對誤差最小的非線性規(guī)劃模型：

其中x(0)(k)為待建立GM（1，1）模型的原始值序列，x^(0)(k)為由式（6）得到的模擬值序列。上面模型中涉及到取絕對值及e-ak等形式，故它是一個非線性規(guī)劃模型。

2.3 使用LINGO建立最優(yōu)化模型

LINGO軟件包是由美國Lindo系統(tǒng)公司（Lindo System Inc.）研制開發(fā)的，用于求解大型數(shù)學規(guī)劃問題的軟件包，它可以求解線性規(guī)劃、整數(shù)規(guī)劃、二次規(guī)劃和非線性規(guī)劃等問題，以及圖論與網(wǎng)絡中的組合優(yōu)化問題[10]。對上面的模型（式（7）），本文就使用該軟件來建模并求解，模型（式（7））轉換成LINGO 11.0的模型如下：

上面模型求解結果中的A和B即為最優(yōu)化GM（1，1）模型的發(fā)展系數(shù)和灰作用量。在對某一問題具體建模時，將原始數(shù)據(jù)序列放在上面模型最后的數(shù)據(jù)區(qū)，即“x0=”的后面，各數(shù)據(jù)間以空格分開，并在模型的最前面和中間指明數(shù)據(jù)個數(shù)，在LINGO 11.0中，可求得該模型的全局最優(yōu)解。另外，上述模型中發(fā)展系數(shù)及灰作用量的變化范圍，可根據(jù)實際情況設為一個較大的范圍，而發(fā)展系數(shù)的變化范圍一般應在內，最終的計算結果應在范圍的中間而不應當取到范圍的邊界，否則，應當擴大相應的范圍。

2.4 以x(1)(m)為初值的最優(yōu)化模型

在文獻[1-2]都提到了以x(1)(n)作為灰色模型微分方程的初值條件，其主要思想是基于灰色系統(tǒng)中充分利用新信息的原則；另外，文獻[1-2]中也提到了選擇最佳的x(1)(m)作為初值條件。在上面的非線性規(guī)劃模型中再加上一個參數(shù)m，并且m的可取值為1到最大數(shù)據(jù)個數(shù)，改變后的模型如下：

模型中其他參數(shù)的意義與上面模型相同，但這樣卻可以得到在各種不同初值條件下的最優(yōu)化模型，經大量數(shù)據(jù)分析發(fā)現(xiàn)，取任意初值得到的最優(yōu)化GM（1，1）模型的模擬精度同樣有了很大的提高。

3 數(shù)據(jù)模擬精度的比較

下面分別以文獻[1]的原GM（1，1）模型、文獻[6]中優(yōu)化初始條件的模型、文獻[9]的改進無偏模型與本文的最優(yōu)化模型對白指數(shù)序列進行模擬。

（1）原始值序列

以白指數(shù)序列x(0)(k+1)=eAk為例進行模擬分析，取k=0，1，…，5，原始序列值如表1。

（2）以表1原始序列分別建立原模型，文獻[6]模型，文獻[9]模型和本文的最優(yōu)模型，并得到它們的模型參數(shù)如表2。

表2中本文模型的數(shù)據(jù)是以x(0)(1)作為初值得到的。分析表2中的數(shù)據(jù)，當 A分別取0.1、0.5、1.0、3.0時最優(yōu)化GM（1，1）模型的還原式分別為：

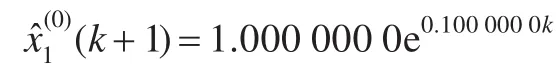
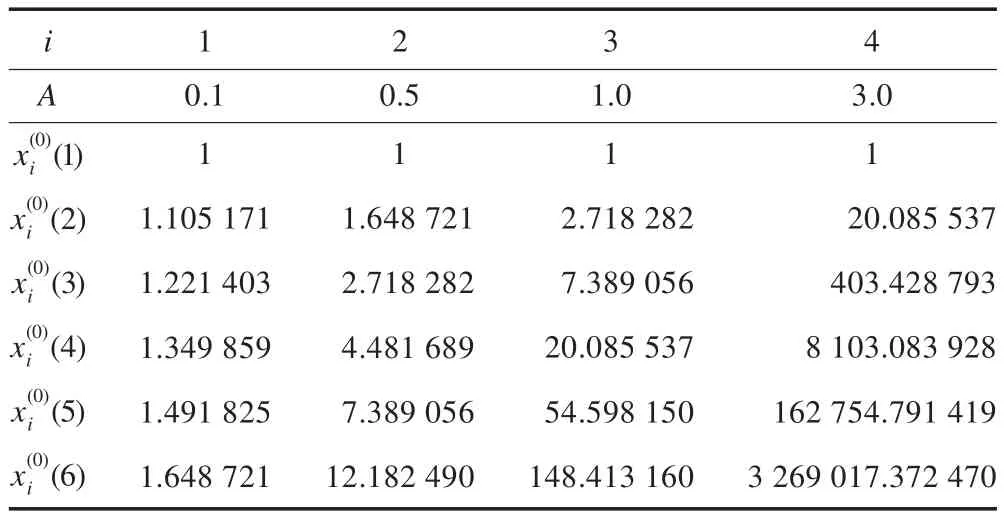
表1 原始值序列

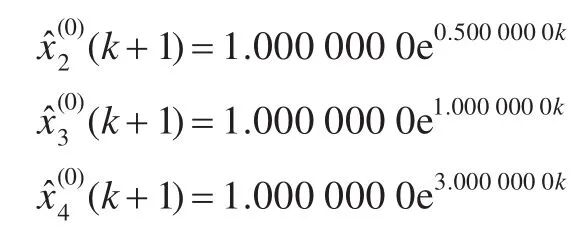
因此，采用本文所述方法建立的最優(yōu)化模型基本上是等于原始白指數(shù)序列的，所以無論是從模擬精度上還是從預測精度上來看，都是新模型優(yōu)于其他模型。

從數(shù)值上看，新模型可能具有白指數(shù)重合律。事實上，根據(jù)前面的非線性規(guī)劃最優(yōu)化模型，有如下的定理。

定理2采用非線性規(guī)劃模型參數(shù)建立的最優(yōu)化GM（1，1）模型具有白指數(shù)重合律。

證明 根據(jù)式（7），當一個模型的實際值與模擬值相等時，最優(yōu)化非線性規(guī)劃模型取得最小值0，此時得到的解也是模型的最優(yōu)解。對白指數(shù)序列：

由定理1，其模擬值序列為：

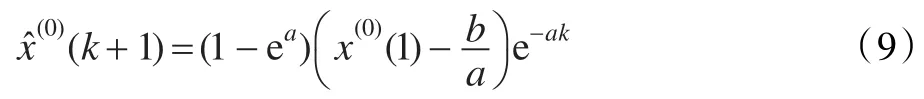
其中，a為GM（1，1）模型的發(fā)展系數(shù)，b為灰作用量。

由式（8）等于式（9）可得：

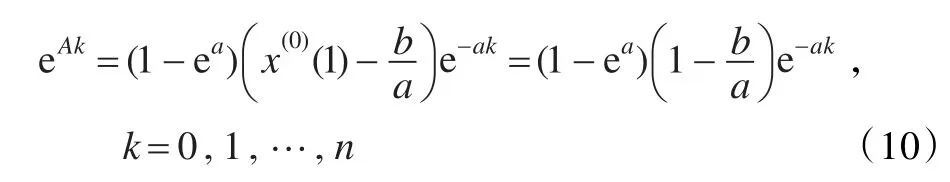
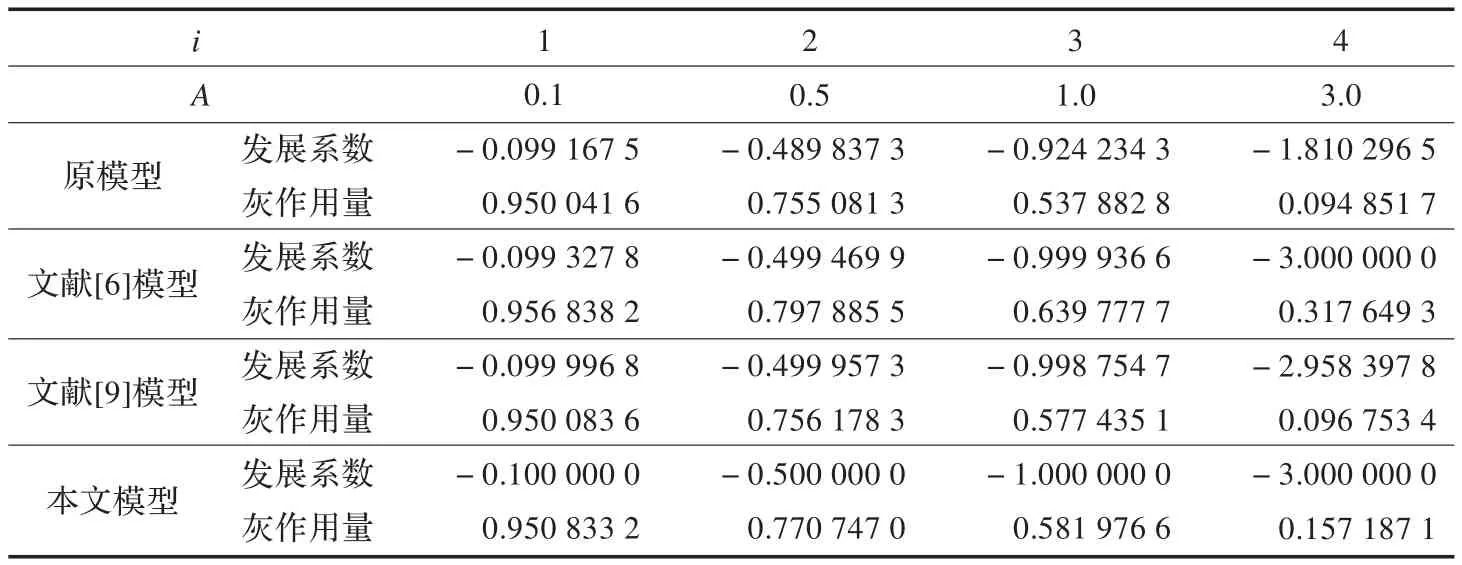
表2 各模型參數(shù)對比

綜上，對白指數(shù)序列 x(0)(k+1)=eAk，當時，由式（7）建立的最優(yōu)化非線性規(guī)劃模型取得最小值0，其對應的最優(yōu)化GM（1，1）模型的模擬值與實際值相等，所以采用新方法建立的最優(yōu)化GM（1，1）模型具有白指數(shù)重合律。

4 實例分析

例1數(shù)據(jù)來源于文獻[6]，其原始數(shù)據(jù)序列為（2.9836，4.4511，6.6402，9.9061，14.7781，22.0464，32.8893）。

利用文獻[1]中鄧聚龍先生的原始灰色建模方法，文獻[6]的改進初始條件建模方法，以及本文的方法分別建立給定數(shù)據(jù)的GM（1，1）模型，得到的時間響應式分別為：

原始建模方法：

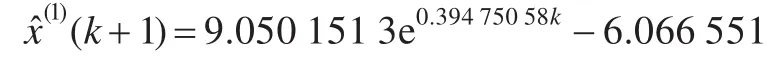
文獻[6]建模方法：

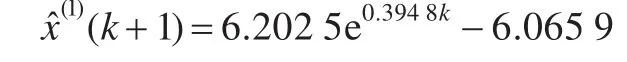
本文方法：

上面各模型具體計算結果如表3。

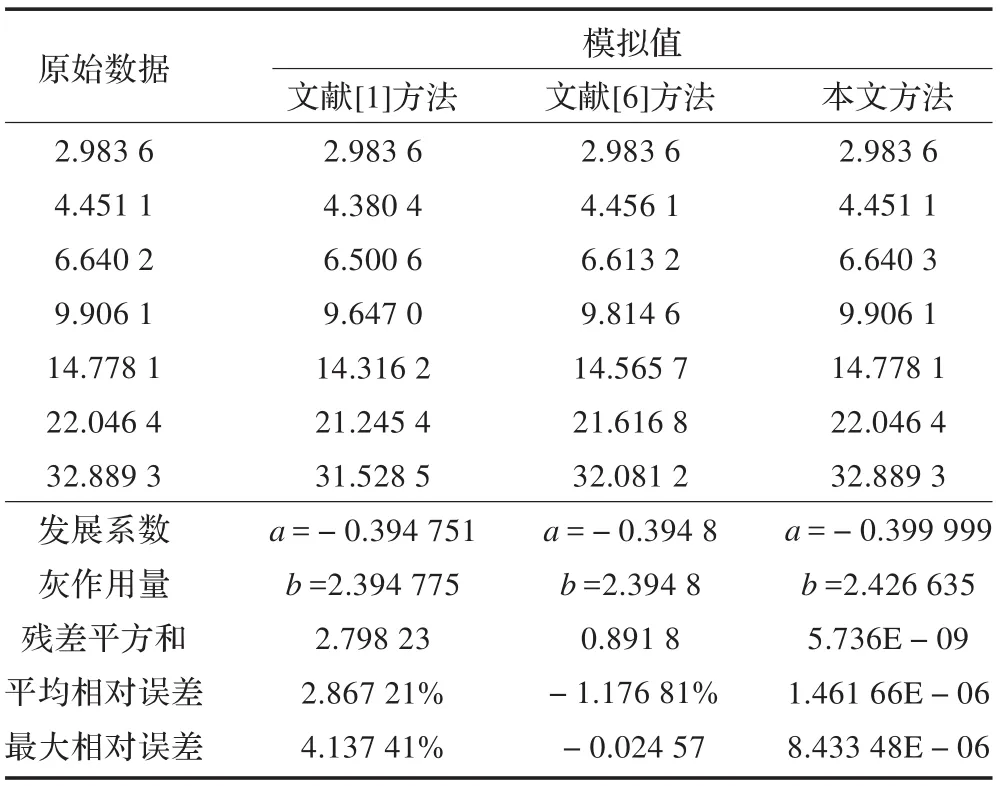
表3 各種建模方法計算結果對比

從表3可以得出以下幾點結論：

（1）采用本文所述方法建立的最優(yōu)化GM（1，1）模型的平均相對誤差和最大相對誤差比其他兩種模型的都要低很多。

（2）對比表3的殘差平方和發(fā)現(xiàn)，本文所述方法和文獻[6]的建模方法的殘差平方和都比原始模型小，這說明采用傳統(tǒng)最小二乘法所得模型即使按誤差平方和最小原則也不是最優(yōu)。

平常中所說的模擬、預測精度高等價于“平均相對誤差小”，筆者認為其合理的原因在于它將“實際值為0.1誤差為0.2”與“實際值為100誤差為0.2”嚴格區(qū)別開來，而“殘差平方和最小”把它們視為同等誤差。

綜合分析上述兩個例子可知，采用本文的新方法建立的GM（1，1）模型的平均相對誤差是最小的，但是發(fā)展系數(shù)及殘差平方和卻各有千秋，這也充分說明，在建立GM（1，1）模型時，應當根據(jù)實際需要來選擇一種最優(yōu)的建模方法，而在評價一個GM（1，1）模型時，應當綜合分析各種因素，并最終確定GM（1，1）模型的利用價值。當然，正如文獻[1]所說，對于一個GM（1，1）模型，一般應當要求每個數(shù)據(jù)的相對誤差小于20%，但最好是小于10%；要求模型的平均相對誤差小于20%，但最好是小于10%。這也是評判一個GM（1，1）模型好壞的基本標準。

5 結束語

本文給出了一種利用建立非線性規(guī)劃模型的方法來建立基于平均相對誤差最小的最優(yōu)化GM（1，1）模型的方法。對比其他很多的優(yōu)化方法，該方法具有如下的一些優(yōu)越性：

（1）采用這種方法建立最優(yōu)化GM（1，1）模型對任何形式的數(shù)據(jù)序列都是有效的；不會像其他方法那樣對某些數(shù)據(jù)序列有效，而對另一些數(shù)據(jù)優(yōu)化效果卻不明顯，甚至起不到優(yōu)化效果。

（2）由于LINGO是一套設計用來使構建和求解線性、非線性和整數(shù)優(yōu)化模型更快、更容易和更有效的功能強大的工具，利用本文的建模方法建立的非線性規(guī)劃模型，可直接利用LINGO 11.0求其全局最優(yōu)解，操作簡單，易于理解，而不必像其他方法那樣經過麻煩的處理過程后才能得到相應的解。

（3）本文建立的最優(yōu)化GM（1，1）模型是針對平均相對誤差最小這個目標建立的，當然在建立非線性規(guī)劃模型時還可以附加上其他的一些約束條件，如要求最大相對誤差達到什么樣的水平，或者殘差平方和達到什么樣的水平等，但是正如文章引言部分述的，一般人們所說的“殘差”有兩種，一種是另一種是前者一般應用于根據(jù)GM（1，1）模型估計發(fā)展系數(shù)a和灰作用量b，而后者主要應用于分析所建立的GM（1，1）模型的模擬精度及預測精度，事實上，按模型殘差平方和最小的評價標準建立的最優(yōu)模型也不是原始灰色模型，應是由后者導出的最優(yōu)化模型，此處不再贅述。

[1]劉思峰，黨耀國，方志耕，等.灰色系統(tǒng)理論及其應用[M].5版.北京：科學出版社，2010：146-197.

[2]黨耀國，劉思峰，王正新，等.灰色預測與決策模型研究[M].北京：科學出版社，2009：101-180.

[3]Yang Shan，Wei Yong.Direct discrete grey model based on non-homogeneous exponential sequence[J].Journal of Grey System，2011，9（4）.

[4]曾波，劉思峰.近似非齊次指數(shù)序列的DGM（1，1）模型直接建模法[J].系統(tǒng)工程理論與實踐，2011，2（31）：297-301.

[5]Xie Naiming，Liu Sifeng，Yang Yingjie，et al.On novel grey forecasting modelbased on non-homogeneousindex sequence[J].Applied Mathematical Modeling，2013，37（7）：5059-5068.

[6]Wang Y H，Dang Y G，Li Y Q，et al.An approach to increase prediction of GM（1，1）model based on optimization ofthe initialcondition[J].ExpertSystemswith Applications，2010，37：5640-5644.

[7]Li J J，Wei Y，Zhou R.The optimized background value of the GM（1，1） model which based on non-homogenous index series[J].Journal of Systems Science and Information，2010（9）：149-156.

[8]徐華峰，方志耕.優(yōu)化白化方程的GM（1，1）模型[J].數(shù)學的實踐與認識，2011，41（7）：163-167.

[9]Ji P R，Zhang J，Zou H B，et al.A modified unbiased GM（1，1）model[J].Grey Systems：Theory and Application，2011，1（3）：192-201.

[10]薛毅.數(shù)學建模基礎[M].北京：北京工業(yè)大學出版社，2004：80-184.