隔振器動力學參數的測試方法研究

王 杰， 趙壽根, 吳大方， 羅 敏

(1.北京航空航天大學航空科學與工程學院， 北京 100191； 2.中國空間技術研究院，北京 100086)

引 言

近年來，國內外航天技術取得了快速的發展，航天器種類和功能日趨多樣化，結構形式日趨復雜。目前，以高分辨率遙感衛星為代表的高精度航天器是研究熱點之一，其具有嚴格的定位指向精度和分辨率要求，如美國最近發射的KH-13 偵查衛星地面分辨率高達0.05 m，這使得航天器各擾動部件傳遞到光學有效載荷的振動量級需衰減到微米甚至納米量級，從而使得該類型的振動控制具有非常大的挑戰性[1，2]。常用的振動控制方法有吸振、隔振和阻尼減振，為了使得動量輪、CMG的低頻姿態控制力矩傳遞到航天器本體結構上而衰減其高頻擾動，隔振是較為適合的一種方法。

從上世紀90年代初美國第一次將三參數微振動隔振器應用到哈勃望遠鏡以來，微振動隔振技術已經發展了20多年，隔振類型也從單一的被動隔振發展為主被動一體化的新技術[3～8]。其中以霍尼韋爾公司的Davis等人為代表發展了多種高性能的微振動隔振器，分析了其內在的隔振機理，給出了阻尼系數和剛度系數的試驗機械阻抗曲線擬合獲取方法，該方法能得出單一的阻尼、剛度數值，擬合誤差較大，沒有考慮粘性流體的阻尼、剛度系數隨頻率的變化規律及其對隔振性能的影響[9～11]。阻尼系數傳統的測試方法有半功率帶寬法、自由衰減法等[12,13]，這些方法的前提假設均為小阻尼，因此并不適合測試大阻尼隔振器的阻尼系數。常用的阻尼系數測試設備有萬能材料試驗機、凸輪試驗系統和高頻疲勞試驗機等，由于微振動隔振器的振幅為微納米量級，上述測試方法和測試設備也很難滿足精度要求。此外，大多數的微振動隔振器均為多參數模型，內含多個結構組件，因而很難直接測量得到內部組件的阻尼系數，從而給隔振器的設計、測試和性能優化增加了難度。

為解決上述難題，本文采用機械阻抗等效的方法，將多參數模型簡化為等效兩參數模型，并設計了相應的測試平臺，采用遲滯環法測試等效兩參數模型的動力學參數，進而反推出多參數模型中的剛度和阻尼系數。在試驗得到各組件動力學參數的基礎上，建立測試對象的Simulink仿真模型，將測試結果與仿真結果進行比對，以驗證本文方法的有效性。

1 機械阻抗等效理論

1.1 五參數模型

如圖1所示為一種航天器流體微振動隔振器的五參數模型，其包含剛度系數k1,k2,k3,k4和阻尼系數c。其中剛度系數k4與阻尼系數c串聯，然后與剛度系數k3并聯，組成一個三參數模型塊，其整體與剛度系數k2串聯，然后與剛度系數k1并聯。三參數模型塊代表樣機的內芯，k2代表樣機的內筒剛度，k1代表樣機的外筒剛度。阻尼系數c主要由內芯油腔內的硅油因受擠壓作用通過小孔，進而產生剪切效應耗散能量而產生，由于流體具有可壓縮性，在流動過程中將同時產生與阻尼系數c串聯的體積剛度k4。因隔振器的質量較小，故在計算時可忽略其質量，如圖2所示。

圖1 五參數模型

圖2 簡化五參數模型

由機械阻抗理論可知，彈簧元件的機械阻抗為Zk=k，阻尼元件的機械阻抗為Zc=jωc；并聯系統的總阻抗等于各要素阻抗之和，總的力為各要素力的和，串聯系統各要素所受到的力相等，總阻抗的倒數等于各要素阻抗倒數之和[14]。由圖2可知，三參數模型塊的機械阻抗Z1為

(1)

式中 拉普拉斯算子s=jω，ω為振動圓頻率，又因其整體與剛度系數k2串聯，然后與剛度系數k1并聯，因此五參數模型的總機械阻抗為

(2)

令

(3)

(4)

(5)

由此式(2)可簡寫為

(6)

1.2 模型等效

為了設計、使用和性能參數測試方便，五參數模型可進一步簡化為如圖3所示的三參數模型，其物理參數有剛度系數kA，kB和阻尼系數cA，kB與cA串聯，然后與kA并聯。

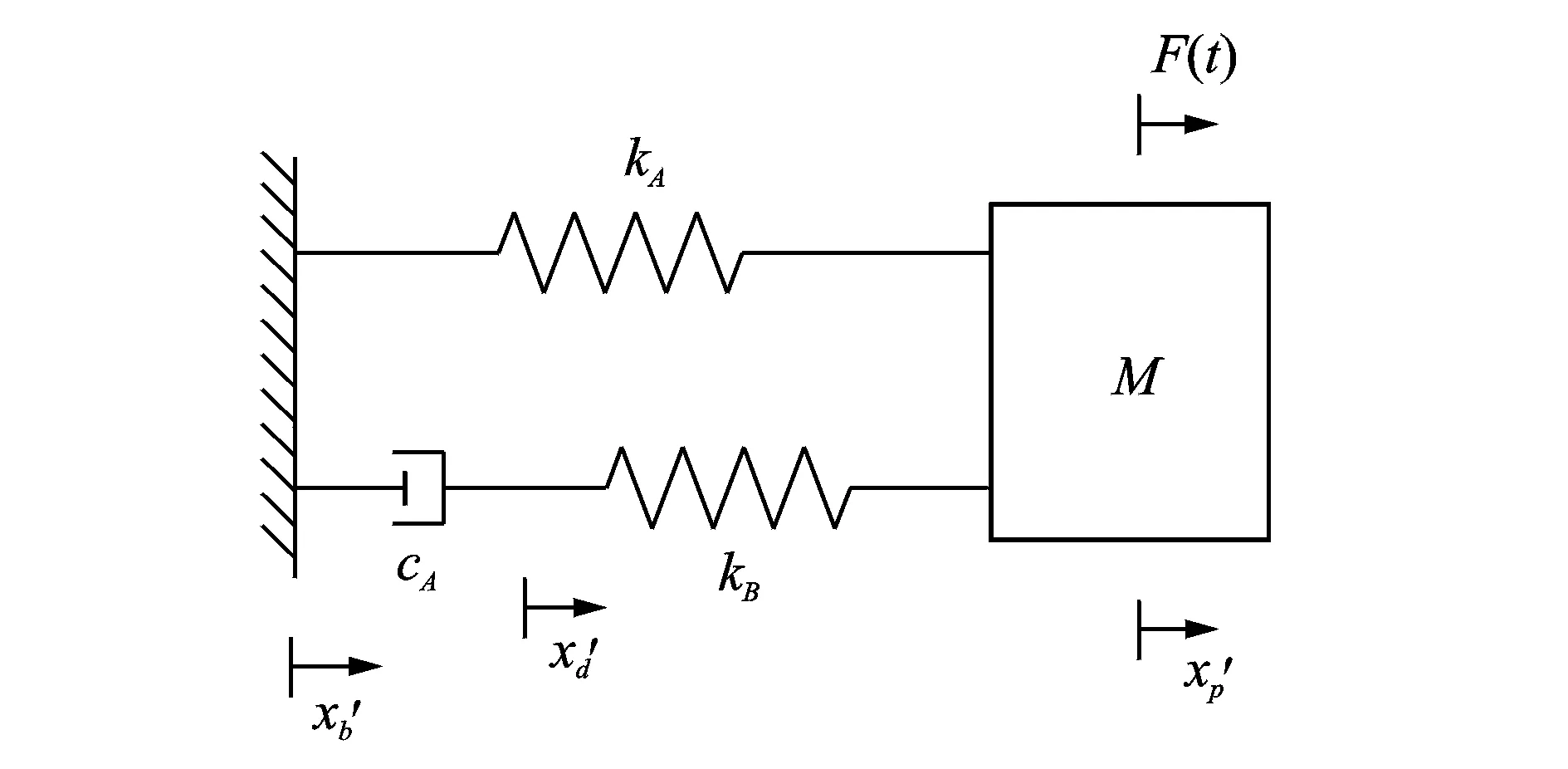
圖3 三參數模型

同理，在計算時略去其質量，由機械阻抗理論可得其機械阻抗ZT的表達式，如下式所示

(7)

上式可進一步化簡為：

(8)

(9)

(10)

由式(6)，(8)可知，二者形式相同，因此令對應項相等，如下式所示

(11)

求解方程則可得到

(12)

由上式可知，將五參數模型等效為三參數模型時，等效參數由式(12)獲得。

1.3 等效兩參數模型

圖4 等效兩參數隔振器模型

同樣，圖3所示三參數模型可進一步等效為如圖4所示的等效兩參數模型，其剛度系數k與阻尼系數c′并聯。由機械阻抗理論可知，等效兩參數模型的機械阻抗Z2為

Z2=k+sc′

(13)

令式(8)，(13)相等可得

(14)

解出cA，kB的表達式為

(15)

(16)

通過以上步驟，就將隔振器整體動力學參數與各組件性能參數聯系起來。

2 試驗測試

2.1 等效動力學參數c′和k的測試原理

對于如圖4所示的隔振器整體等效兩參數模型，依據微振動隔振器的特點，本文采用遲滯環法測試其等效阻尼系數c′和等效剛度系數k。測試原理如下：阻尼力與位移之間因阻尼作用而形成遲滯環[15]，如圖5所示。

在圖5(a)中，其關系可由如下橢圓方程表示

圖5 遲滯環曲線

(17)

式中Fc′為阻尼力，y為振動位移響應，A為振動位移幅值。由其數學表達式可知，橢圓的短軸包含等效阻尼系數c′的信息，如下式所示

(18)

式中L為橢圓短軸的長度。L可由橢圓的面積S得出，如下式所示

(19)

綜合式(18)，(19)可得等效阻尼系數c′的表達式為

(20)

由于實際測試的力包含系統剛度引起的彈性力，即Fc′+ky，故測試的遲滯環將旋轉一定的角度，如圖5(b)所示。由于彈性力在振動循環中不消耗能量，故橢圓面積不變。在實際應用中，由數值積分可得到橢圓的面積Sk，式(20)變為

(21)

由斜橢圓的斜率可得等效剛度系數k為

k=tanθ

(22)

進而由式(15)，(16)可得cA，kB的數值，由式(12)可得阻尼系數c和剛度系數k4的表達式為

(23)

2.2 等效動力學參數c′和k的測試裝置

如圖6所示為測試裝置示意圖，主要包括承力工裝、力傳感器、激光位移傳感器、激振器、數據采集與分析系統、控制系統、功率放大器等。在試驗過程中，控制系統首先發出定頻正弦信號經功率放大器放大后傳輸到激振器，進而激勵隔振器。隔振器右端與激振器連接，端部為激光位移傳感器(采用德國Polytec激光位移測量系統，型號為psv-200，其位移精度為0.1 μm)，左端通過力傳感器與承力工裝連接。數據采集與分析系統采集力傳感器與位移傳感器的力信號與位移信號，從而得到該頻率下力與位移之間的遲滯環。改變激勵頻率后，重復上述步驟，即可得到各個頻率下的遲滯環曲線。在試驗過程中，整個系統接地線去除電噪聲的影響，并采用帶通濾波濾掉直流分量和其他干擾頻率。圖7所示為測試裝置的實物圖，圖8所示為測試得到的遲滯環曲線。

圖6 等效阻尼系數測量裝置示意圖

圖7 測試裝置實物圖

圖8 測試遲滯環

2.3 剛度系數的測試裝置

如式(12)，(15)，(16)，(23)所示，式中剛度系數k1，k2，k3是由等效阻尼系數c′和等效剛度系數k計算隔振器動力學參數cA，c，kB，k4時所必需的參數，本文采用附加質量法獲取各個組件的剛度系數值。測試裝置如圖9所示，主要包括控制系統、功率放大器、激振器、大質量塊、承力工裝、隔振器、力傳感器、數據采集與分析系統等，其中大質量塊與激振器采用懸掛方式安裝。控制系統首先發出正弦掃頻信號經功率放大器放大后傳輸到激振器，進而激勵整個系統。大質量塊與激振器通過力傳感器B連接，其左側與隔振器連接。隔振器的左端通過力傳感器A與承力工裝連接，約束其端部位移。數據采集與分析系統采集兩個力傳感器的力信號，通過數據處理，可得系統的傳遞率曲線，如圖10所示為測試外筒剛度k1時所得的傳遞率曲線。

圖9 剛度系數測試裝置示意圖

圖10 力傳遞率曲線

試驗中剛度系數測試步驟如下:

(1)測試樣機外筒剛度系數k1。

(2)測試樣機內筒剛度系數k2。

(3)測試樣機內芯無油時的剛度系數k3。

各個組件的剛度測試結果如表1所示。

由式(12)可得等效三參數模型的剛度系數kA=9.085×106N/m。

表1 剛度系數測試結果

3 Simulink仿真分析

由式(12),(15),(16)可知，kB與k4,cA與c為一一對應關系，cA,kB和等效參數c′,k為單值關系。此外，由圖1,3可知，微振動隔振器內含粘性流體，阻尼系數c,cA分別與剛度系數k4,kB串聯耦合，由于流動狀態的復雜性，較難從理論上獲得其數值隨頻率的變化規律。為驗證采用機械阻抗等效的方法測試多參數模型中阻尼系數和剛度系數的正確性，將計算得到的振動模型各剛度系數與阻尼系數輸入到仿真模型中，得到隔振器整體的等效阻尼系數c′和等效剛度系數k，將其與試驗結果進行對比，由于各數值的唯一性，通過比較二者誤差的大小即可判斷方法的有效性。在仿真過程中，采用Simulink軟件建立系統的仿真模型，其以系統的運動方程為基礎[16～19]。

如圖3所示，在其右端部施加簡諧力，系統的運動方程為

(24)

將上式兩邊同時作Laplace變換可得

(25)

圖11 三參數時域仿真模型

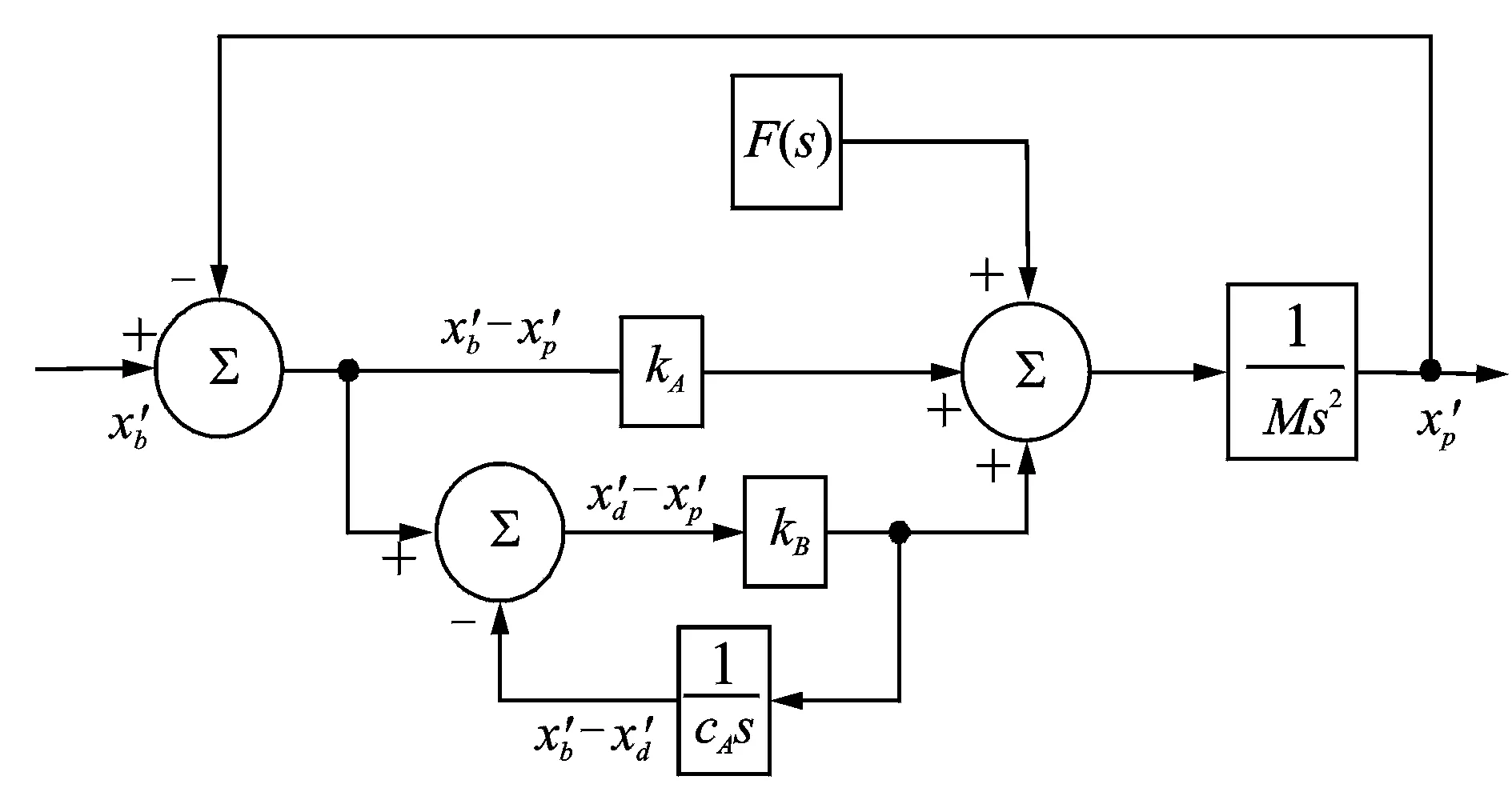
圖12 三參數頻域仿真模型

同理，如圖1所示，系統的運動方程為

(26)

將上式兩側作Laplace變換可得

(27)

由式(26),(27)建立的Simulink仿真模型分別如圖13,14所示，其中xb=0。

圖13 五參數時域仿真模型

圖14 五參數頻域仿真模型

4 試驗、仿真結果及討論

如圖15所示為阻尼系數c，cA曲線圖。由式(12)可知，二者為線性關系，由試驗結果計算得知

cA=0.896c

(28)

隨著頻率的增加，阻尼系數先急劇下降，隨后趨于平穩，且最小的阻尼系數也可達1 500 N·s/m，屬于大阻尼范圍。通過曲線擬合，阻尼系數c近似與頻率成如下函數關系

c=a×fb

(29)

式中a=2.389×106，b=-0.714，f為橫軸頻率坐標。圖16所示為剛度系數kB，k4的曲線圖，隨著頻率的增加，剛度系數緩慢增大。通過曲線擬合可得如下表達式

(30)

式中A1=6.410×106，B1=127 897.600，C1=-955.470，D1=2.050；A2=7.640×106，B2=160 851.530，C2=-1 131.900，D2=2.310。

圖15 阻尼系數曲線圖

圖16 剛度系數曲線圖

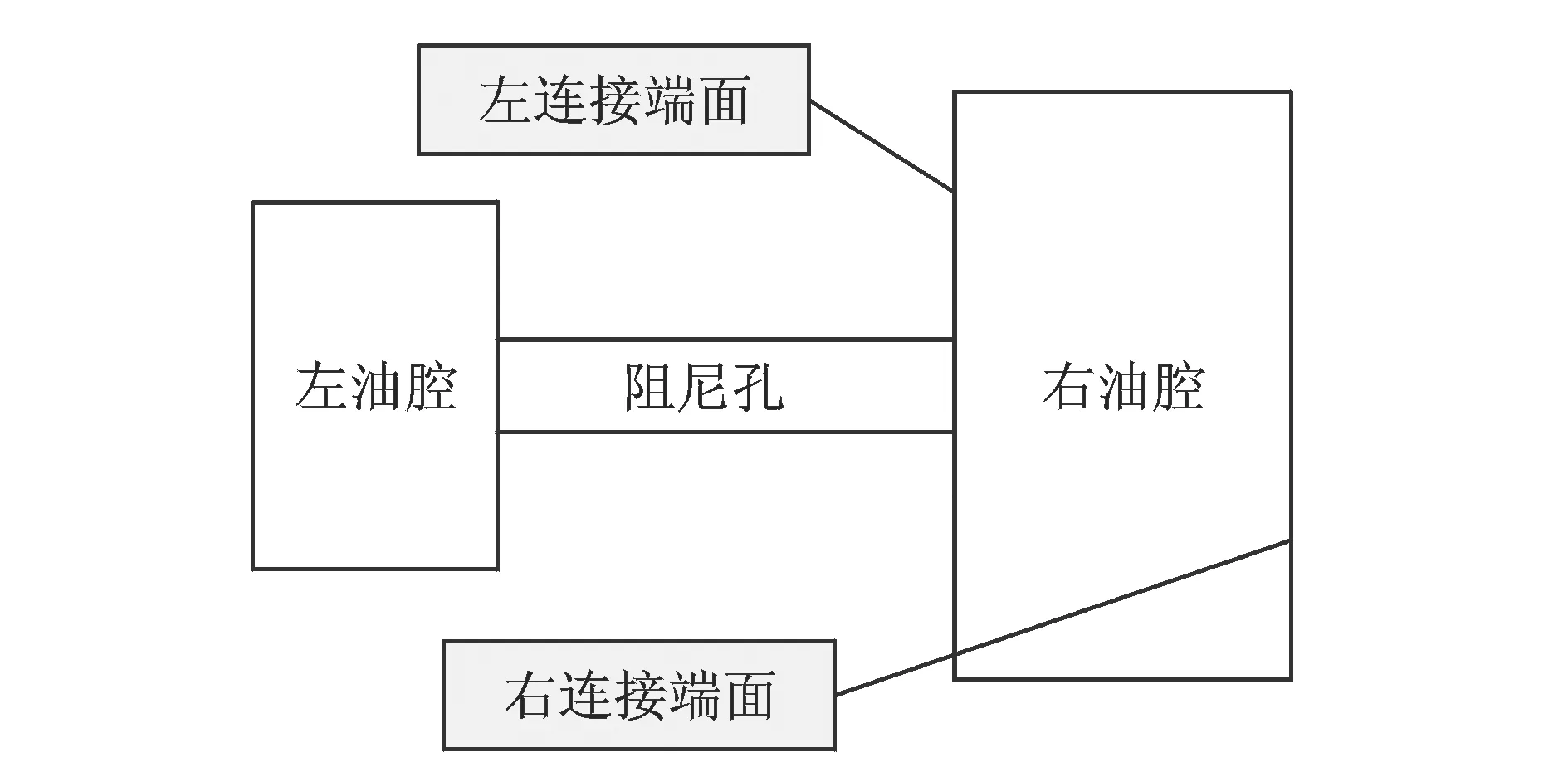
圖17 油腔結構示意圖

圖17所示為隔振器內芯油腔結構示意圖，其內含硅油粘性流體，通過左、右連接端面分別與內筒、外筒相連接，組成隔振器整體樣機。當隔振器受到外力激勵產生彈性變形時，驅動左、右油腔內的流體通過細長阻尼孔往復運動[20]。在低頻時，整個阻尼孔內的流體可充分流動，因此粘性流體的剪切耗能作用強，產生的阻尼系數大。由于流體具有可壓縮性，隨著頻率的增加，阻尼孔內流體的實際流動長度會縮短，中間一段流體幾乎不能為左右油腔內的流體所替代，因此其剪切耗能作用下降，阻尼系數降低。同時由于阻尼孔內流體的流動效應隨著頻率的增加而下降，左右油腔內的流體可抵抗更多的外力，其彈性效應增加，剛度系數增大。

圖18(a)，(b)所示為測試、仿真得出的整體等效阻尼系數c′的對比曲線圖。由圖可知，二者具有較好的一致性，每個頻率點的相對誤差均在5%以內，且最小阻尼系數也可達1 000 N·s/m。圖19(a)，(b)所示為測試、仿真得出的整體等效剛度系數k的對比曲線圖，同樣地，試驗結果與仿真結果的相對誤差均在5%以內，顯示出較好的一致性。仿真輸入力的幅值有50和100 N，從圖中可以看出結果沒有顯著變化。以上結果有效地驗證了采用機械阻抗等效的方法測試阻尼系數和剛度系數的正確性，針對大阻尼粘性流體微振動隔振器，能夠有效地測試出其內在的阻尼和剛度特性，對于隔振設計具有重要的參考價值。

圖18 試驗與仿真所得等效阻尼系數

圖19 試驗與仿真所得等效剛度系數

5 結 論

本文主要針對航天器所用的粘性流體微振動隔振器進行研究。根據該類型隔振器具有大阻尼且振動位移為微米量級的特點，提出采用機械阻抗等效的方法測試其動力學特性參數。應用機械阻抗等效理論將五參數模型轉化為三參數模型，再將其進一步等效為兩參數模型，在此基礎上，自行設計了試驗測試系統，采用遲滯環法測試隔振器整體等效阻尼系數和等效剛度系數。根據系統的物理模型，建立了Simulink仿真模型，將數據處理所得振動模型數據輸入到仿真模型中，得到隔振器整體等效阻尼系數和等效剛度系數，并將其與試驗測試結果相比較，二者具有良好的一致性，有效地驗證了本方法的正確性與可行性。本方法還可得到阻尼系數和剛度系數隨頻率的變化規律，對于隔振設計具有重要的參考價值，其可推廣應用于一般的隔振器阻尼系數和剛度系數的測量。

參考文獻：

[1] 黃文虎, 曹登慶, 韓增堯. 航天器動力學與控制的研究進展與展望[J] . 力學進展, 2012,42(4):367—394.Huang Wenhu, Cao Dengqing, Han Zengyao. Advances and trends in dynamics and control of spacecraft[J]. Advances in Mechanics, 2012,42(4):367—394.

[2] 張振華, 楊雷, 龐世偉. 高精度航天器微振動動力學環境分析[J]. 航天器環境工程, 2009,26(6):528—534.Zhang Zhenhua, Yang Lei, Pang Shiwei. Jitter environment analysis for micro-precision spacecraft[J]. Spacecraft Environment Engineering, 2009,26(6):528—534.

[3] Davis L P, Carter D R, Hyde T T. Second-generation hybrid D-strut[A].Smart Structures & Materials′95[C]. International Society for Optics and Photonics, 1995:161—175.

[4] Hyde T T, Anderson E H. Actuator with built-in viscous damping for isolation and structural control [J]. AIAA Journal, 1996,34(1):129—135.

[5] Vaillon L, Philippe C. Passive and active microvibration control for very high pointing accuracy space systems[J]. Smart Materials and Structures, 1999,8(6):719—728.

[6] Cobb R G, Sullivan J M, Das A, et al. Vibration isolation and suppression system for precision payloads in space[J]. Smart Materials and Structures, 1999,8(6):798—812.

[7] Sullivan J M, Gooding J C, Idle M K, et al. Performance testing for an active/passive vibration isolation and steering system[A].AIAA Dynamics Specialists Conference[C]. Salt Lake City， 1996:87—97.

[8] Vaillon L, Petitjean B, Frapard B, et al. Active isolation in space truss structures: from concept to implementation[J]. Smart Materials and Structures, 1999,8(6):781—790.

[9] Davis L P, Cunningham D, Bicos A S, et al. Adaptable passive viscous damper: an adaptable D-StrutTM[A].1994 North American Conference on Smart Structures and Materials[C]. International Society for Optics and Photonics, 1994:47—58.

[10] Davis P, Cunningham D, Harrell J. Advanced 1.5 Hz passive viscous isolation system[A].35th AIAA SDM Conference[C]. Hilton Head, South Carolina， 1994:1—11.

[11] Davis L P, Workman B J, Chu C C, et al. Design of a D-strutTMand its application results in the JPL, MIT, and LARC test beds[A].AIAA/ASME/AHS/ASC Structures, Structural Dynamics and Material Conference[C]. Dallas, USA, 1992:1 524—1 530.

[12] 戴德沛. 阻尼減振降噪技術[M]. 西安: 西安交通大學出版社, 1986:53—107.Dai Depei. Damping Vibration and Noise Reduction Technology[M]. Xi′an: XI′AN JIAOTONG UNIVERSITY PRESS, 1986:53—107.

[13] 陳奎孚, 張森文. 半功率點法估計阻尼的一種改進[J]. 振動工程學報, 2002,15(2):151—155.Chen Kuifu, Zhang Senwen. Improvement on the damping estimation by half power point method[J]. Journal of Vibration Engineering, 2002,15(2):151—155.

[14] Anderson E, Trubert M, Fanson J, et al. Testing and application of a viscous passive damper for use in precision truss structures[A].AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference[C]. Baltimore,USA，Apr. 1991:8—10.

[15] Oh H U, Izawa K, Taniwaki S. Development of variable-damping isolator using bio-metal fiber for reaction wheel vibration isolation[J]. Smart Materials and Structures, 2005,14(5):928—933.

[16] Putnam D, Eraker J H, Mohl J B. Vibration isolation module for exposed facility payloads[A].Conference and Exhibit on International Space Station Utilization[C]. Cape Canaveral, 2001.

[17] Wilson G W, Wolke P J. Performance prediction of D-Strut isolation systems[A].Smart Structures and Materials′97. International Society for Optics and Photonics[C]. 1997:236—250.

[18] Liu K C, Blaurock C, Mosier G E. Pointing control system design and performance evaluation of TPF coronagraph[A].Astronomical Telescopes and Instrumentation[C]. International Society for Optics and Photonics, 2004:437—448.

[19] Boyd J, Hyde T T, Osterberg D, et al. Performance of a launch and on-orbit isolator[A].SPIE′s 8th Annual International Symposium on Smart Structures and Materials[C]. International Society for Optics and Photonics, 2001:433—440.

[20] Rittweger A, Albus J, Hornung E, et al. Passive damping devices for aerospace structures[J]. Acta Astronautica, 2002,50(10):597—608.