一種盲源提取方法及其在滾動軸承故障特征提取中的應用
王宏超, 陳 進, 董廣明
(上海交通大學機械系統與振動國家重點實驗室, 上海 200240)
引 言
由于各種干擾源和噪聲的影響,來自現場傳感器的軸承故障信號非常復雜,直接對這些信號進行故障特征提取是非常困難的。盲源提取(Blind source extraction,BSE)技術的出現為這個問題的解決提供了新的技術和手段。BSE技術是近10年來新興并引起廣泛重視的一類信號處理方法,有時也叫盲信號抽取,它源于盲源分離(Blind source separation, BSS)技術。BSS技術在語音、通訊和醫學工程等領域都有著成功的應用[1~3],但其在旋轉機械故障診斷中的應用有著較大的局限性,其原因可歸結為如下[4]:瞬時混合模型的幅值不確定性和順序不確定性;適用于振動信號的多通道卷積混合盲分離算法迄今仍沒有令人滿意的解決方案;源物理相關性的不確定性;源數的估計存在偶然性;盲源分離要求系統具有可逆性,但實際工程中很多機械系統是不可逆的。BSE相對于BSS有以下優點[5]:充分利用被提取對象的先驗信息;僅僅提取感興趣的信號;無需估計源的數目;計算量小;特別適用于源數較多而感興趣信號較少的情況(如機械系統)。綜上所述,BSE在某種程度上彌補了BSS的缺點。在既有的BSE技術中,約束獨立成分分析最具代表性,其最先由Wei Lu等人于2000年提出[5]。隨后Wei Lu分別將CICA用于圖像盲分離與醫學信號盲分離[6,7],相對于傳統獨立成分分析(Independent component analysis, ICA)方法取得了不錯的效果。Zhang Z L將CICA方法加以改進,提出了基于形態的CICA方法并將其用于微弱腦電信號的盲源提取[8],通過仿真合成信號和實際腦電信號驗證了所提出方法的正確性及實際應用價值。在旋轉機械故障診斷方面,CICA也取得了一定的應用[9],在文獻[9]中Wang Z Y等將CICA用于滾動軸承的故障診斷中,并通過仿真信號和滾動軸承全壽命加速疲勞實驗信號驗證了CICA在旋轉機械盲信號提取中的有效性。然而,上述CICA在盲源提取中的成功應用都需要以下兩個前提條件:用于構建參考信號的目標源信號基本周期的精確估計;正確參考信號的構建。如文獻[9]所驗證,不正確參考信號的選取會造成誤判或漏判的結果。此外,用于構建參考信號的目標源信號基本周期的估計值也會對提取結果造成很大的影響。然而在滾動軸承的實際工程應用中由于安裝精度、制造誤差及滾子相對于滾道的隨機滑動等影響,都會造成目標源故障信號的實際基本周期與理論計算基本周期的偏差。這樣就限制了CICA方法在旋轉機械故障診斷中的應用。在文獻[10]中,Barros等提出了一種基于最佳估計延時的能快速提取周期信號的盲提取方法。但所述方法本質上還是以目標信號的基本周期或基本周期的整數倍作為最佳延時。本文首先用基于二階統計量的自相關函數算法估計目標源信號基本周期[10],再與基于高階統計量的固定點算法相結合的盲提取方法成功用于復雜運行環境下滾動軸承故障信號的盲提取[11,12],此種方法在某種意義上來講是對文獻[10]所述方法的改進。此外,此種方法相對于CICA方法具有較強的魯棒性:只需要大致估計目標信號的基本周期并將其作為所述方法相關步驟的基本周期即可。同文獻[9],將所述方法用于滾動軸承全壽命加速疲勞實驗故障信號的盲提取,并與文獻[9]CICA在滾動軸承全壽命加速疲勞故障信號盲提取中的應用作以比較,得出前者相對于后者具有更強的目標源信號基本周期估計誤差的容錯性。
1 問題的提出
假設有一多維觀測信號矢量x(t)可表示為
x(t)=As(t)+n(t)
(1)
式中s(t)=[s1(t),s2(t),…,sn(t)]T是n×1滿足統計獨立性的源信號矢量,x(t)=[x1(t),x2(t),…,xm(t)]T是m×1的混合信號矢量,矩陣A={aij}是由混合參數aij構成的m×n階的混合矩陣。n(t)=[n1(t),n2(t),…nm(t)]T是與源信號矢量統計獨立的加性噪聲矢量。

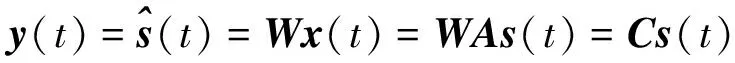
(2)
式中 矩陣C=(ci,j)n×n被稱為混合-分離復合矩陣,該矩陣的每一行與每一列有且僅有一個非零元素。瞬時混合模型的混合和分離過程如圖1所示。
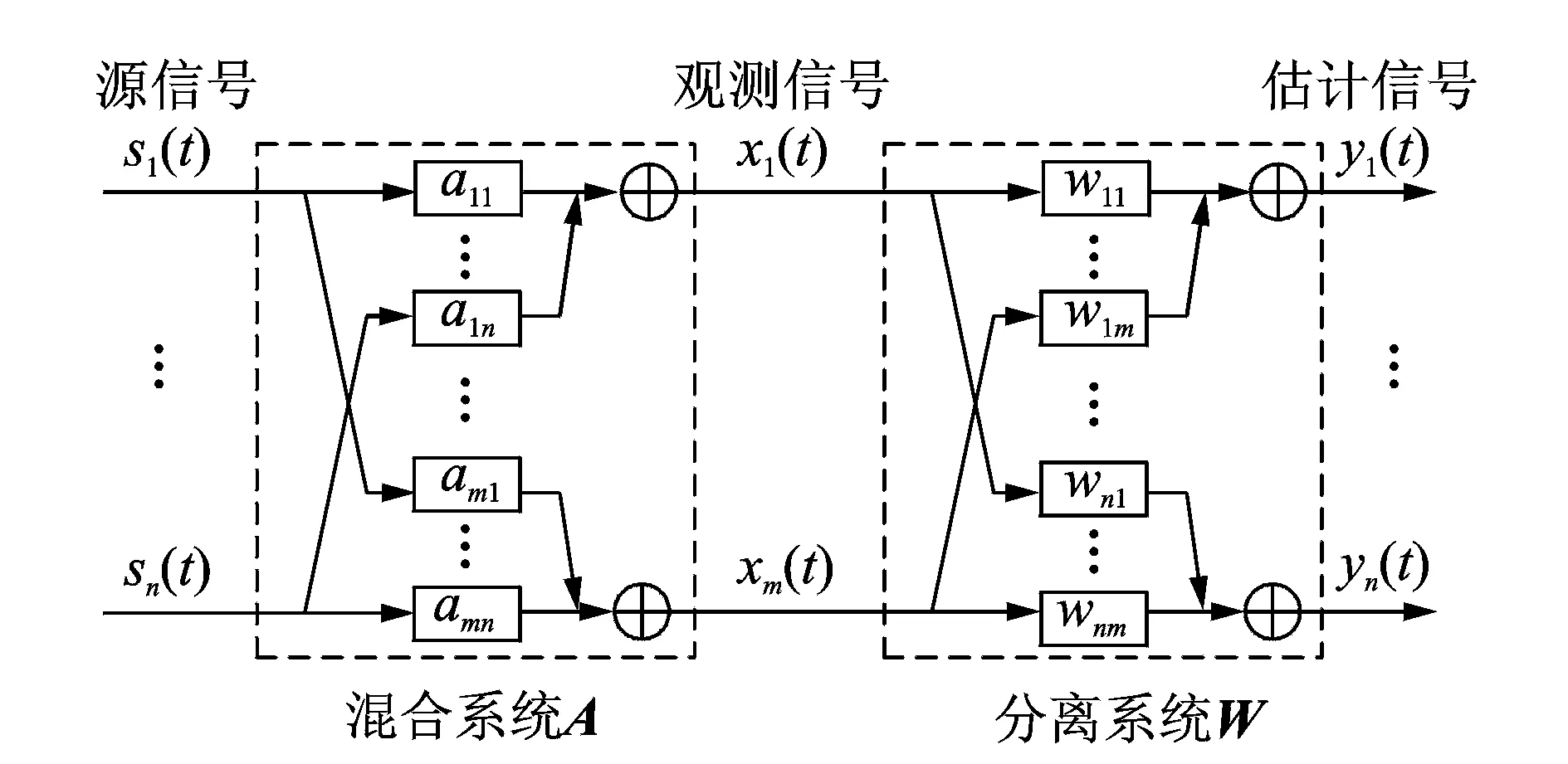
圖1 瞬時混合和分離模型示意圖
根據傳感器數m和源數n的關系,瞬時ICA模型可劃分為3種:
當m=n時,此時混合矩陣A是方陣,稱為平方ICA模型;
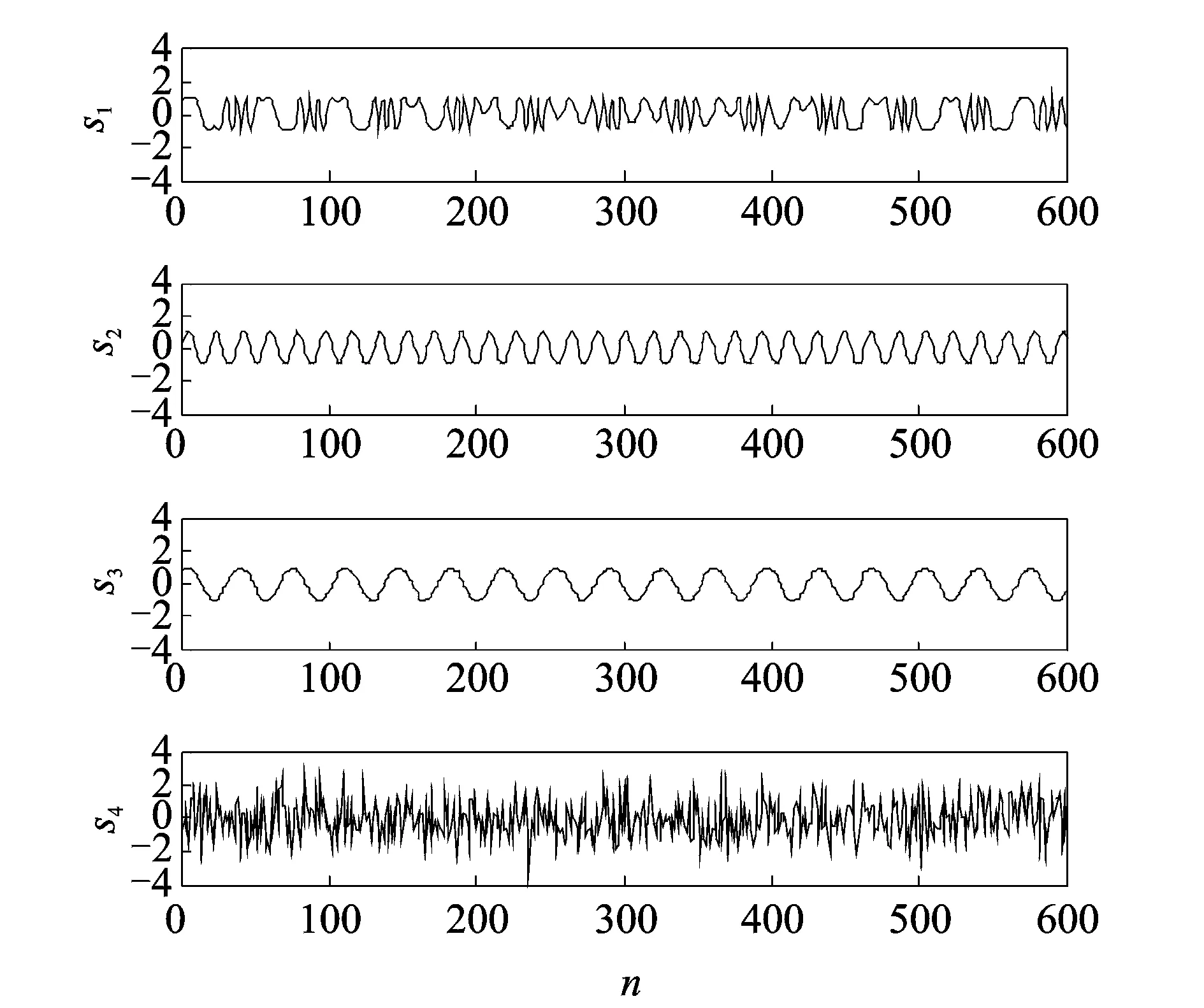
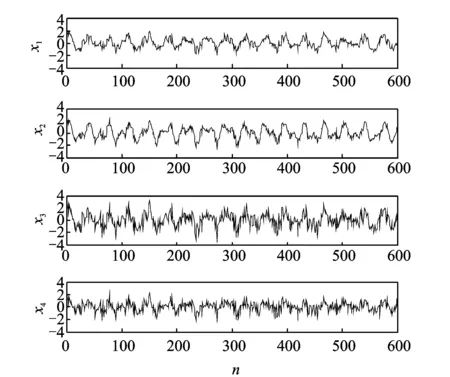
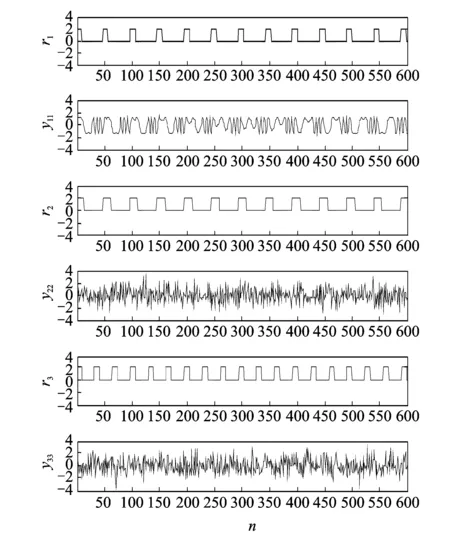
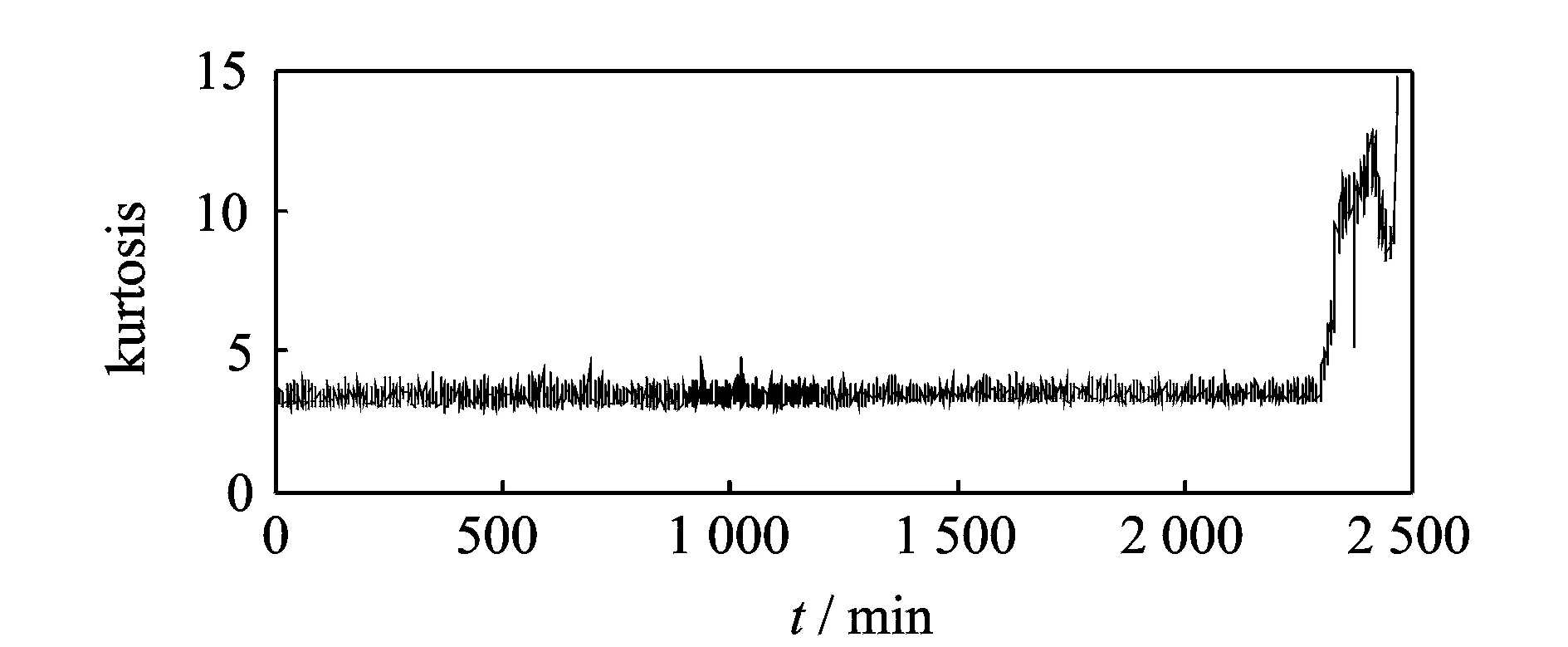
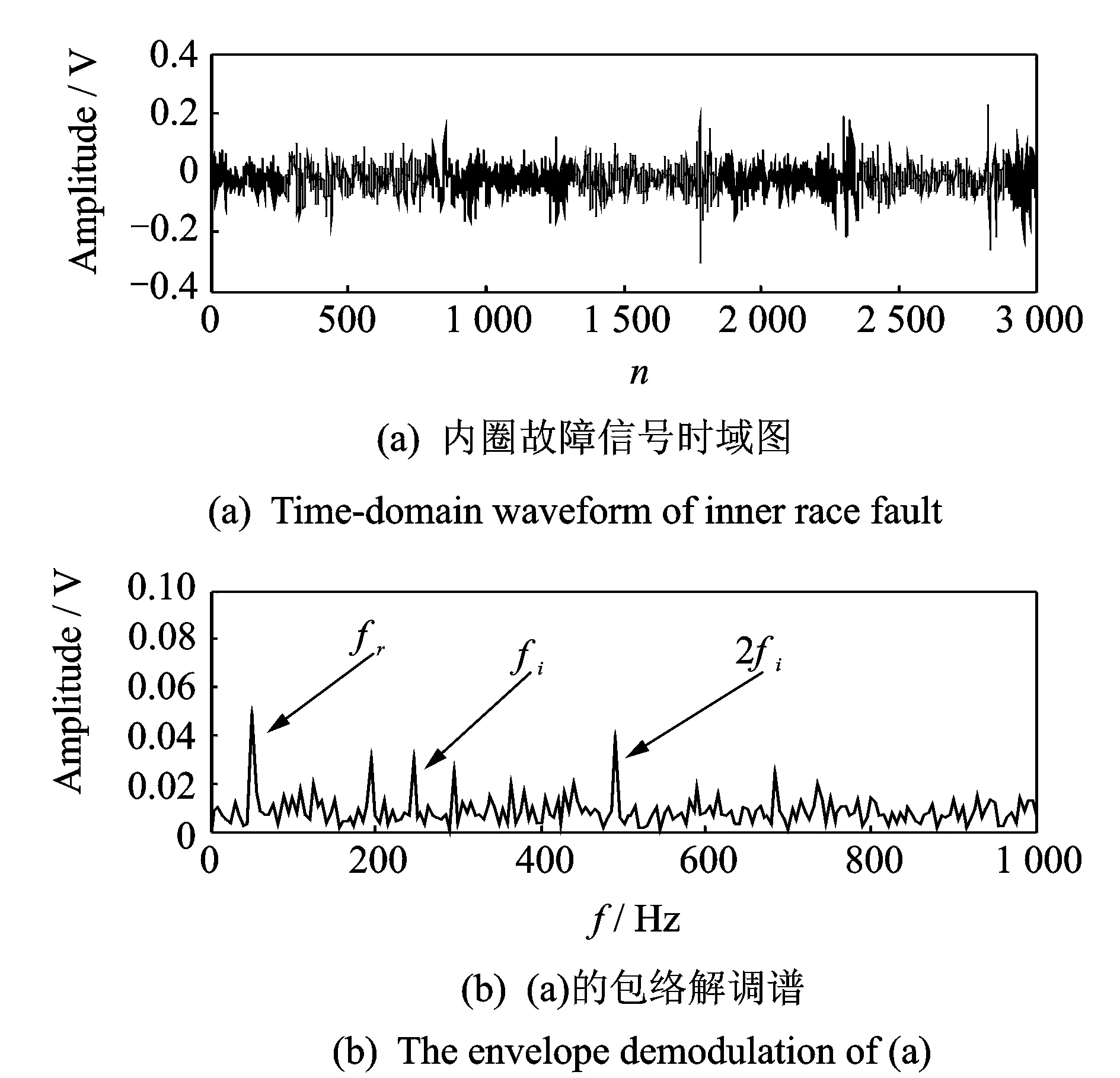
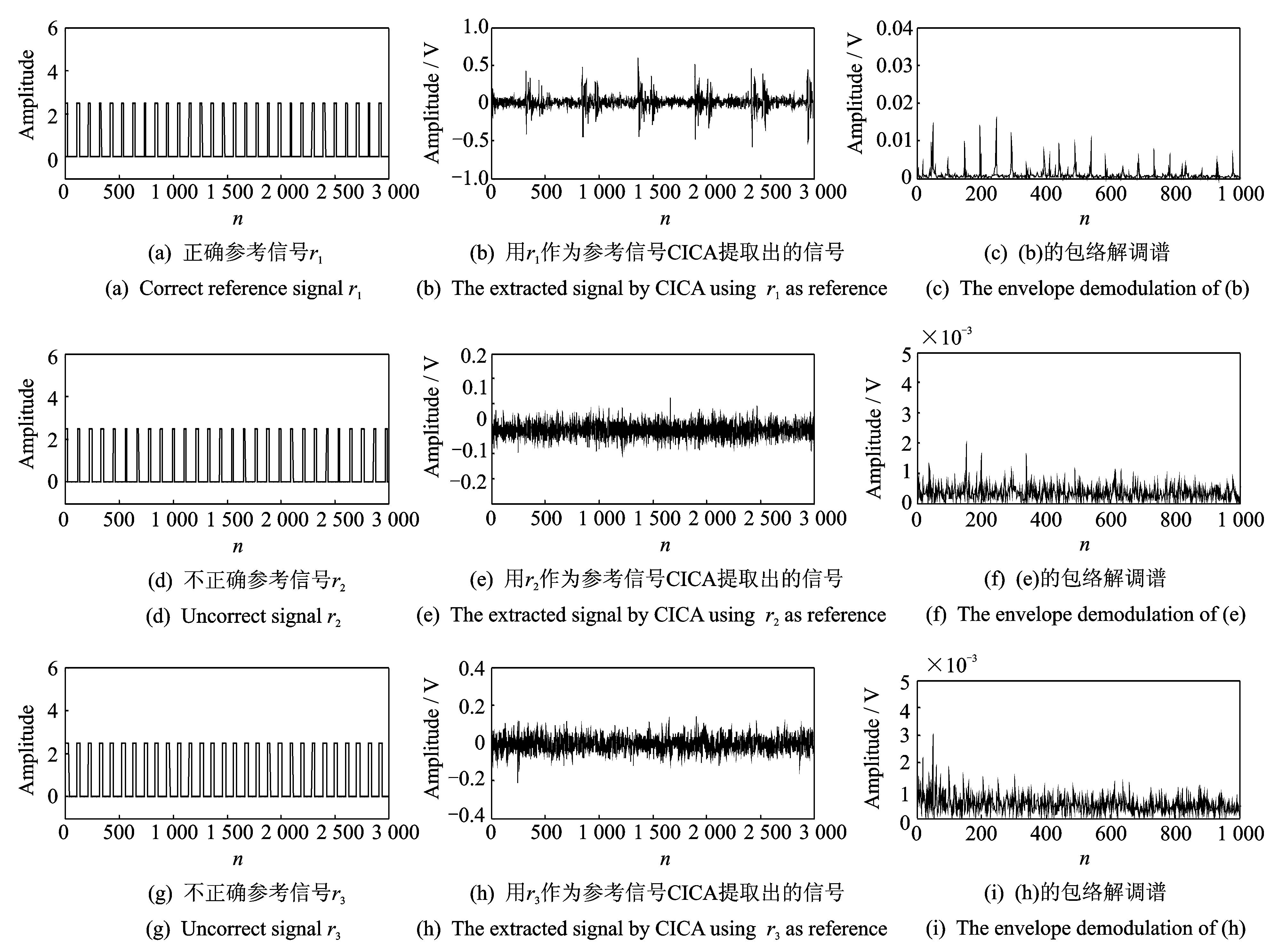
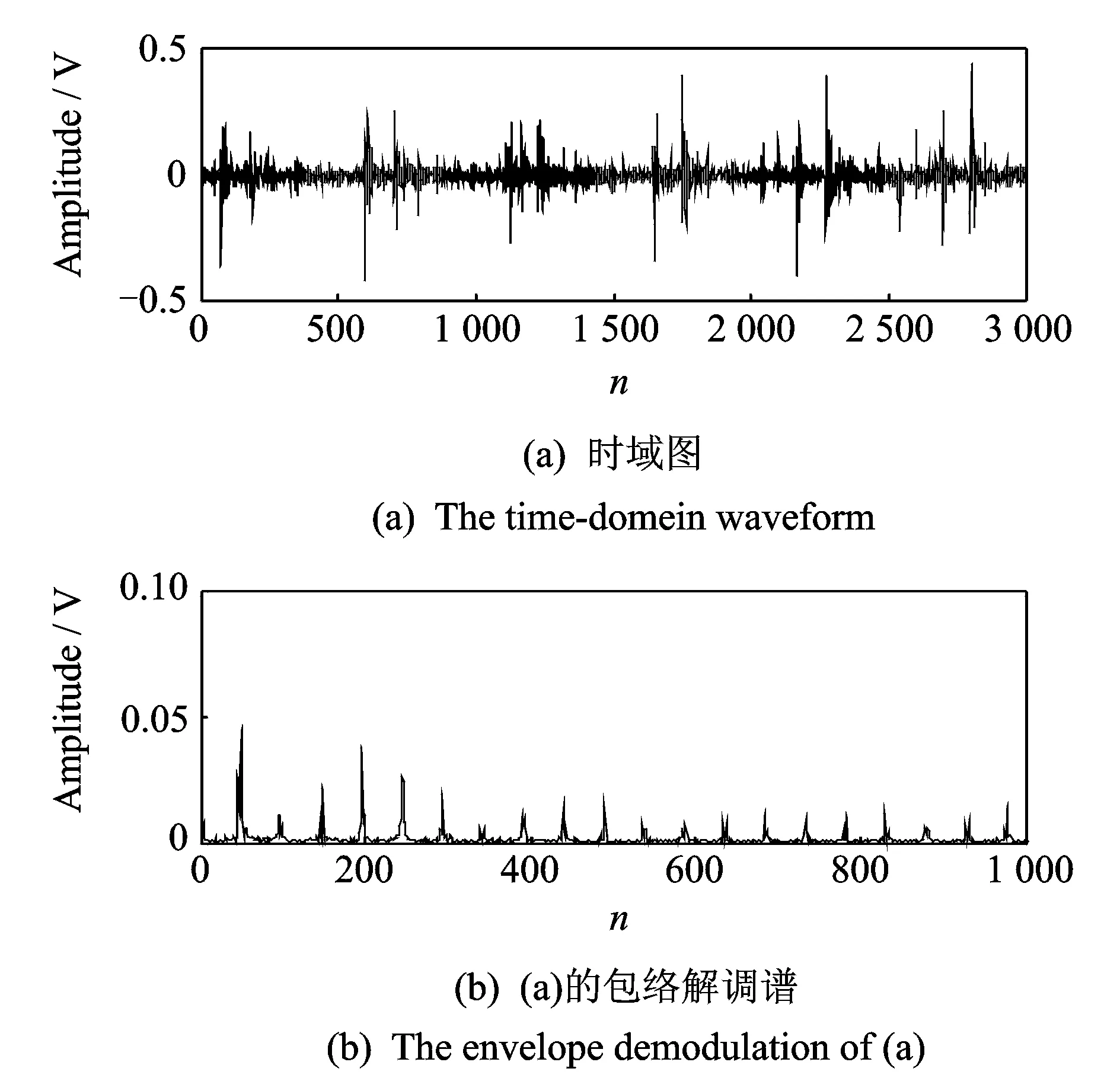
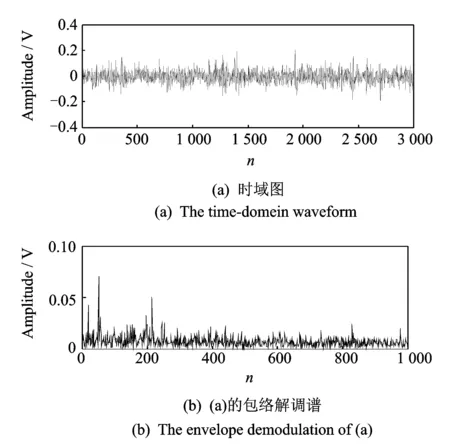
當m 當m>n時,稱為超定ICA模型。 本文是基于平方ICA模型展開討論的。 此外,為提高計算速度及簡化本文算法,首先對觀測信號x(t)進行白化處理,即 (3) 式中V稱為白化矩陣。以下所述所有觀測信號x(t)均為白化信號。 對于要提取的目標源信號si,假設對一特定整數τ*有以下關系式成立 (4) 式中sj為其他非目標源信號,k代表時間,τ*即為最佳時間延時[10]。 J(W)=E{y(k)y(k-τ*)}=WTE{x(k)x(k-τ*)T}W (5) 在約束條件‖W‖=1下,最大化公式(5)所示的目標函數就可以提取出目標函數si。因為對于目標函數si,其關于延時為τ*的延時自相關函數是一個大于0的正值,而其他非目標源函數sj關于τ*的延時自相關函數都將為0。 忽略Rx(τ*)與Rx(τ*)T的微小差距,利用標準梯度算法,可得出文獻[10]的算法 (6) 式中Rx(τ*)=E{x(k)x(k-τ*)T}。盡管文獻[11]所述方法具有算法簡潔、計算速度快等優點,但是其具有以下缺點: (1)即使目標源信號si關于τ*的時延自相關函數E{si(k)si(k-τ*)}>0,但不能保證其他所有非目標源信號sj關于τ*的時延自相關E{sj(k)sj(k-τ*)}=0(j≠i); (2)即使所有源信號嚴格獨立不相關,但是在實際計算中由于用源信號有限點數的算術平均來代替源信號的數學期望,就會造成源信號的自相關計算值不為0[15,16],即:即使有下式成立 (7) 但也極有可能下式成立 (8) 綜上所述,文獻[10]所述基于二階統計量的盲提取方法受上述兩點限制,其盲提取性能的穩定性及精確性就受到了很大的影響,甚至會提取出非目標源信號。由于本文的研究是基于瞬時線性ICA基礎上的,也就是假設源信號在物理意義上是相互獨立的,所以可以用高于二階統計量的更高階的統計量去改善文獻[10]所述的方法。以下是所述方法的介紹。 所用的方法大概分為3個步驟,如圖2所示。 圖2 所述方法流程圖 各個步驟的具體計算過程如下: (1)目標源信號基本周期的估計:當滾動軸承發生故障時,其故障基本周期可以由理論計算頻率的倒數得出; (2)初始目標源信號及分離矩陣計算: 式(5)所示的目標函數 (9) (10) (11) 由式(10)可得出式(11)的相應算法如下 (12) (3)初始分離矩陣W的進一步優化: (13) 為提高算法對野點和沖擊噪聲的魯棒性,可以采用文獻[11]的改進固定點算法 (14) 式(13)或(14)收斂時,即可得到最佳分離矩陣W。以下的仿真及實驗結果均取式(13),(14)二者之間效果最好的。 圖3 原始信號 圖4 觀測信號 圖5 不同盲提取方法得到的結果 圖3為4個信號,其中圖3中的s1為準周期信號,s2為正弦信號,s3為余弦信號,s4為隨機高斯白噪聲。在Matlab中任意產生一隨機4×4階的矩陣A對4個信號進行混合。圖4為混合后的觀測信號。提取目標信號是s1。圖5為用不同方法得到盲抽取結果。其中圖5中的y1為文獻[10]所述方法的盲抽取結果,得到了錯誤的抽取結果;圖5中y2為文獻[15]所述方法的提取結果;圖5中的y3為本文所述方法的提取結果。雖然直觀上看y2與y3要都為正確的目標源信號s1。可以用下式來對提取結果y2和y3的盲抽取精度進行比較 (15) 將s1和y2,s1和y3分別代入式(15)得到的PI值分別為22.4和47.6 dB,由此,所述方法相對于文獻[15]所提出的方法具有更高的提取精度。 圖6 基于不同參考信號的CICA抽取結果 圖6是CICA方法用不同參考信號對觀測信號的盲抽取結果。其中參考信號r1為正確的參考信號,將其與觀測信號一起輸入到CICA算法中,y11為抽取的結果。從y11可以看出CICA在正確輸入參考信號的情況下可以很好地抽取出目標信號s1;不改變參考信號r1的方波周期,而改變方波的寬度即得到參考信號r2,將r2與觀測信號一起輸入到CICA算法中,y22為抽取的結果,可見抽取不出目標信號。同樣不改變r1方波的寬度,而改變方波的周期得到參考信號r3,將r3與觀測信號一起輸入到CICA算法中,y33為抽取的結果,可見仍抽取不出目標信號。由此,CICA算法的能否成功應用在某種程度上取決于參考信號的能否正確設計,其使用受到了很大的限制。而分別將r1,r3的周期作為所述方法的基本估計周期(或基本周期的整數倍),均能提取出目標源信號s1。限于篇幅限制在此不再給出抽取結果。 同樣采用文獻[9]中的滾動軸承全壽命加速疲勞實驗數據。實驗具體實施步驟及數據采集參數均可見參考文獻[9]。選用和文獻[9]同一個故障軸承進行分析,文獻[9]給出了故障軸承的全壽命周期的均方根值(Root mean square, RMS)值曲線圖。本文給出故障軸承全壽命周期的峭度指標曲線圖,如圖7所示,因為峭度指標對滾動軸承發生故障時的沖擊特征更為敏感。 圖7 實驗軸承全壽命周期的峭度值 對第2 304組數據進行分析。將3個加速度傳感器采集到的信號作為觀測信號,其時域圖如圖8所示(注:文獻[9]的時域圖縱坐標單位為加速度,而本文的縱坐標單位為電壓)。 圖9為圖8所示信號相對應的包絡解調譜,從圖9中均無法很好地提取出滾動軸承內圈故障通過頻率fi=246 Hz及其諧頻:圖9(a)雖然能大致提取出內圈故障通過頻率,但其諧頻及調制頻率即轉頻提取效果并不好;圖9(b),(c)的提取結果會造成誤判或漏判。 將本文所述方法用于上述觀測信號,提取出的信號的時域圖及其包絡解調譜圖如圖10所示,由包絡解調譜可以看出其很好的提取出內圈故障通過頻率fi=246 Hz及其諧頻。在用所述方法對觀測信號進行處理時,估計目標信號的基本周期設置為T=(1/fi)×fs=104(用點數表示,可參考文獻[9])。 圖11是基于不同參考信號的CICA盲提取結果,其中圖11(a)的r1是正確參考信號:周期為T=104(采用點數表示,可參考文獻[9]);方波寬度為20(點數),圖11(b)為盲抽取的信號,圖11(c)為11(b)的包絡解調譜,由此看見,CICA很好地提取了內圈故障通過頻率;改變圖11(a)的周期,即T′=106,方波寬度不變,得到參考信號r2如圖11(d);圖11(e)為盲提取結果的時域圖,圖11(f)為圖11(e)的包絡解調譜,提取不出內圈故障頻率;同樣,不改變圖11(a)的周期,而改變方波寬度(方波寬度由20設置為30)即得到參考信號r3如圖11(g);圖11(h),(i)分別為盲提取結果的時域圖及包絡解調譜,同樣提取不出內圈故障特征頻率。可見,CICA能否正確地提取故障特征頻率,對精確參考信號的設計有著苛刻的要求(參考信號的周期及方波形狀的微小改變都會對CICA提取結果造成很大的影響)。在工程實際應用中,由于設計精度、安裝誤差及滾動體的隨機滑動都會造成滾動軸承理論計算故障頻率與實際故障頻率的誤差。而本文所述的方法只需要大致估計目標源信號的基本周期即可。圖12為將T=106作為目標源信號的估計周期,用本文所述方法得到盲提取信號的時域圖及其相應的包絡解調譜,仍可以提取出內圈故障特征頻率。說明了本文所述方法相對于CICA方法有較強的目標源信號周期誤差的容錯性。 圖8 實驗觀測信號 圖9 實驗觀測信號的包絡解調譜 圖10 所述方法的盲提取結果 圖13為文獻[15]所述方法的提取效果,從其包絡解調譜中無法提取中滾動軸承內圈故障通過頻率。 圖11 用不同參考信號CICA的提取結果 圖12 用所述方法以T=106作為估計基本周期的提取結果 圖13 用文獻[15]所述方法的盲提取結果 本文將一種盲提取方法用于復雜運行環境下滾動軸承故障信號的盲提取中,取得了不錯的結果。并通過仿真驗證了所述方法相對于其他盲提取方法有較高的精度;通過仿真和實驗驗證了所述方法相對于CICA方法具有目標源信號基本周期誤差容錯性的優點;此外,所述方法只需要估計目標源信號的基本周期即可,而CICA方法不但需要目標源信號基本周期的精確估計,而且還需要構建準確的參考信號,其使用相對于所述方法具有較大的局限性。 參考文獻: [1] Hyvarinen A, Oja E. Independent component analysis:algorithms and applications[J]. Neural Networks, 2000, 12:411—430. [2] Choi S J, Cichocki A, Park H M, et al. Blind source separation and independent component analysis:A review[J]. Neural Information Processing-letters and Reviews, 2005, 6(1):1—57. [3] James C J, Gibson O J. Temporally constrained ICA:An application to artifact rejection in electromagnetic brain signal analysis[J]. IEEE Transaction on Biomedical Engineering, 2003, 50(1):1 108—1 116. [4] Antoni J. Blind separation of vibration components:rinciples and demonstrations[J]. Mechanical Systems and Signal Processing 2005, 19:1 166—1 180. [5] Lu W, Rajapakse J C. Constrained independent component analysis, in:Advance in Neural Information Processing Systems, vol.13(NIPS 2000)[M]. MIT Press, Cambridge, MA, 2000:570—576. [6] Lu W, Rajapakse J C. Approach and applications of constrained ICA[J]. IEEE Transaction on Neural Networks, 2005, 16(1):203—212. [7] Lu W, Rajapakse J C. ICA with reference[J]. Neurocomputing, 2006, 69:2 244—2 257. [8] Zhang Z L. Morphologically constrained ICA for extracting weak temporally correlated signals[J]. Neurocomputing, 2008, 71:1 669—1 679. [9] Wang Z Y, Chen J, Dong G M, et al. Constrained independent component analysis and its application to machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011, 25:2 501—2 512. [10] Barros A K, Cichocki A. Extraction of specific signals with temporal structure[J]. Neural Computation, 2001, 13(9):1 995—2 003. [11] Cichocki A, Amari S I. Adaptive Blind Signal and Image Processing. Learning Algorithms and Applications[M]. New York:John Wiley & Sons,2002. [12] Hyvarinen A, Oja E. A fast fixed-point algorithm for independent component analysis[J]. Neural Computation, 1997, 9(7):1 483—1 492. [13] Sabri K, Badaoui M E, Guillet F, et al. A frequency domain-based approach for blind MIMO system identification using second-order cyclic statistics[J]. Signal Processing, 2009, 89:77—86. [14] Belouchrani A, Meraim K A, Cardoso J F, et al. A blind source separation technique using second-order statistics[J]. IEEE Transactions on Signal Processing, 1997, 45(2):434—444. [15] Zhang Z L, Zhang Y. Robust extraction of specific signals with temporal structure[J]. Neurocomputing, 2006, 69:888—893. [16] Bermejo S. Finite sample effects in higher order statistics contrast functions for sequential blind source separation[J]. IEEE Signal Processing Letters,2005, 12(6):481—484.2 方法的提出
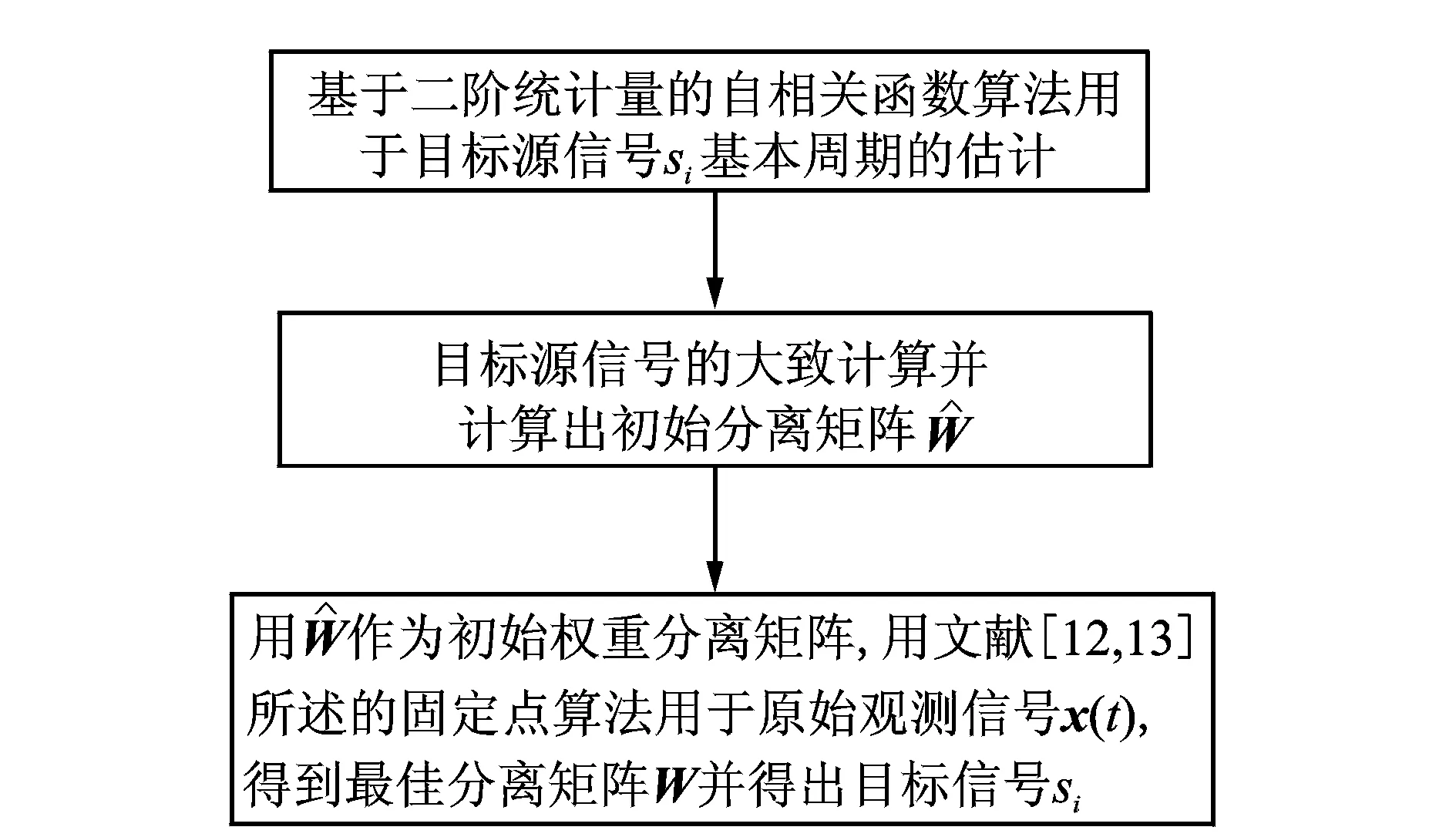
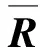
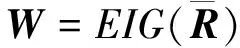
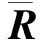


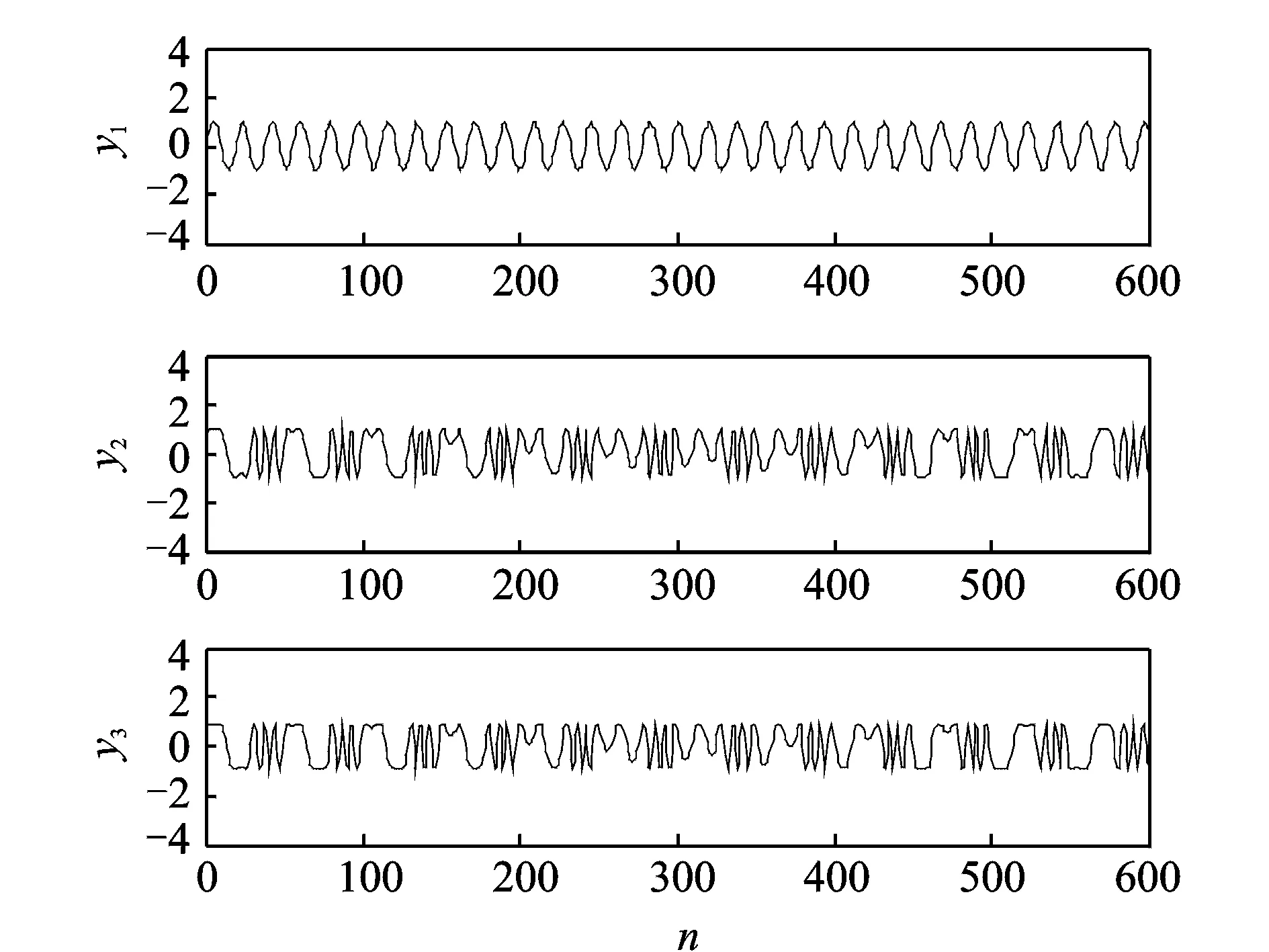
3 仿 真
4 實 驗
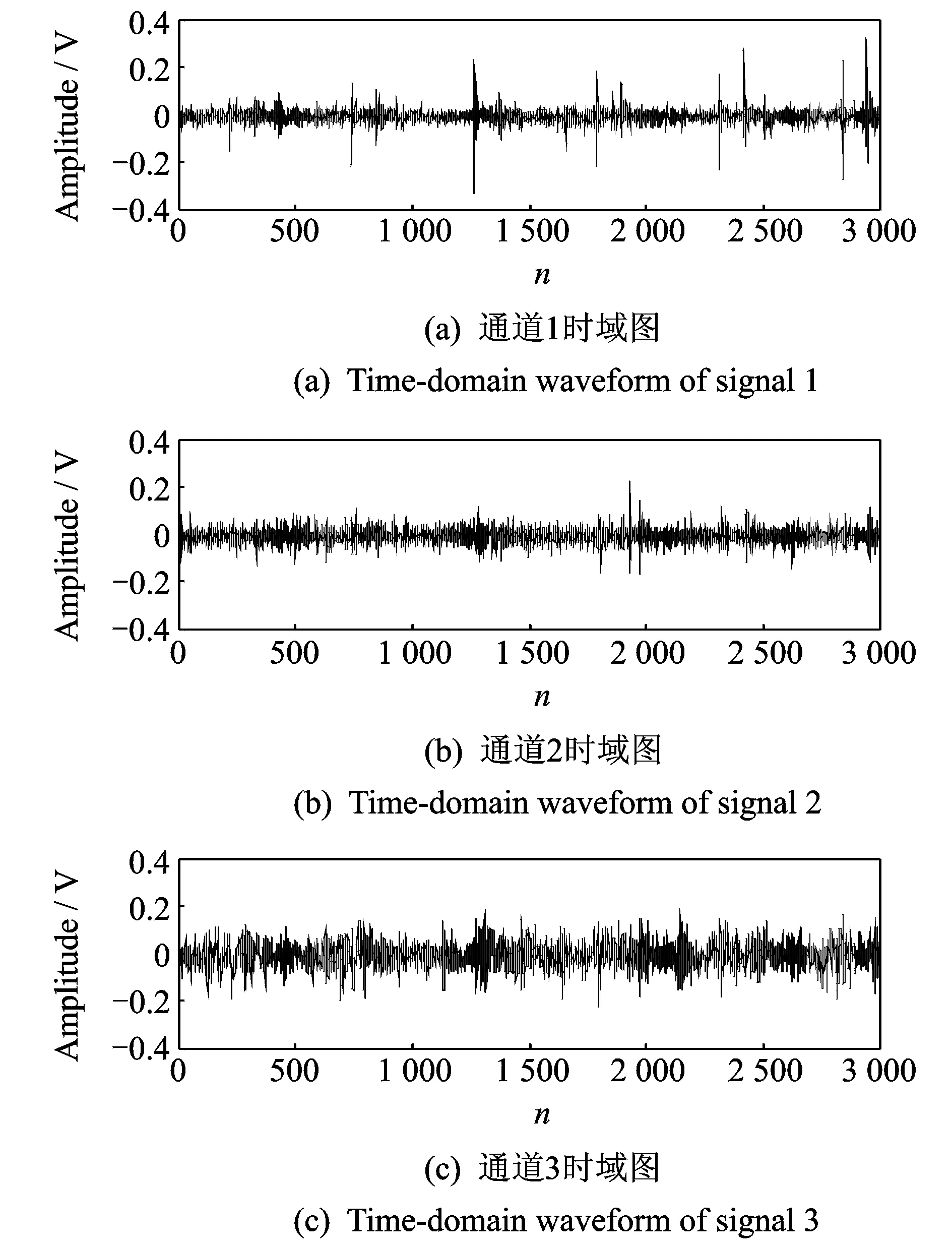

5 結 論

