均值與偏度約束下CVaR最小投資組合優化模型研究

大連交通大學 吳 雷 姜昱汐 李博達 東北大學秦皇島分校 李 剛

一、引言

投資組合問題是現代金融理論研究的起源和熱點，其核心思想可概括為：如何把財富配置到不同的資產中，以達到確保收益、分散風險之目的。自1952年Markowitz建立均值-方差模型定量研究資產組合選擇問題后，人們相繼提出許多其他的投資組合模型。現有模型側重于對收益前兩階矩（均值和方差）的關注，大多忽視了收益的三階矩（偏度）風險。Arditi（1975）指出偏度越大意味著低收益率出現的概率越小而高收益率發生的概率越大，忽略偏度得出的最優組合可能是一個無效的組合，但未予實證。張樹斌等（2004）對構建的均值-方差-偏度模型進行靈敏度測試，進一步證實了偏度的引入極大改變投資組合的選擇。高岳林等（2010）構建了均值和VaR約束下偏度最大的多期投資組合模型。遲國泰等（2009）、吳灝文（2011）在均值-方差模型基礎上引入偏度大于等于零約束，建立了正態分布下的均值-方差-偏度的貸款組合優化模型，實證表明偏度的引入能降低貸款組合的風險，但沒有討論非正態分布下的情形。

在上述帶有偏度的模型中，仍然使用方差或VaR來度量組合的風險。由于方差將收益的向上波動和向下波動都視為風險，不符合實際，夸大了組合的風險；VaR雖是當前備受推崇的風險測度方法，但Artzner（1997）證明了VaR不滿足風險測度一致性公理中的次可加性，且對尾部風險關注不足，因此方差和VaR均不是完善有效的風險度量方法。Rockafellar和Uryasev于2000年在VaR的基礎上首次提出CVaR概念，并將其與VaR比較后發現：CVaR滿足次可加性、具有凸性等優點，且證實CVaR更能反映投資組合風險。林東旭等（2004）討論了正態分布下的均值-CVaR模型及其有效前沿。但肖甲山（2008）對我國股票收益率檢驗后發現其不服從正態分布，進而討論了非正態分布下的均值-CVaR模型，并對CVaR加以離散化和線性化處理后將模型轉化為線性規劃問題，且在求解CVaR的同時得到了VaR，實證表明其比均值-方差模型更能降低極端風險。

在綜合考慮以上因素后，本文選用CVaR來測度組合的風險，引入偏度大于等于0約束來降低組合的風險，構建均值和偏度約束下CVaR最小的投資組合優化模型，并利用股票市場數據對模型加以驗證。

二、模型構建

（一）目標函數建立 CVaR的全稱是ConditionalValueatRisk，一般譯為條件在險價值，其含義是：在一定的置信水平下，損失超過VaR的條件均值，反映了超額損失的平均水平，又可稱為尾部VaR或平均超額損失。相對于方差和VaR，CVaR有顯著的優點：對尾部風險考慮更為充分，滿足次可加性，具有凸性等。故CVaR也被認為是當前較為完善有效的一種風險測度方法。因此，本文選用CVaR度量投資組合風險，目標函數就是使CVaR最小Uryasev，即：

根據CVaR的定義，可以得到：

其中，f（x，r）表示投資組合的損失函數，θ代表置信水平。

通過式（2），很難直接得到CVaR，因為式中含有VaR這個內生參數。本文根據Roclcafellar（2002）設計的方法，通過構造輔助函數，并對CVaR進行離散化處理，得到CVaR的近似表達式：

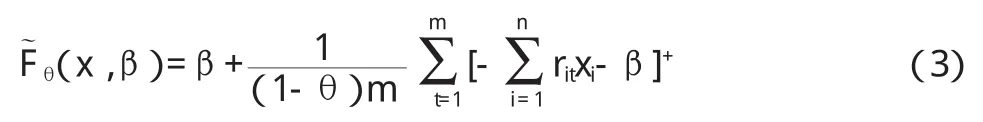
由式（3）得到的β值就是VaR，這把VaR和CVaR兩者有效的聯系起來，在求解CVaR的同時順便得到VaR。

綜合（1）式和（3）式，目標函數可轉化為：

（二）約束條件的建立 具體如下：

（1）收益率約束。理性投資者追求在既定的收益下使風險最小，對于投資組合的收益，一般使用收益率的數學期望（均值）表示，即

（2）偏度約束。偏度（skewness）定義為收益與均值之差三次方的數學期望與標準差三次方的比值，其計算公式為：

其中：σ為收益率的標準差，ri為收益率的第i個樣本數據，r為平均收益率。

圖1 不同偏度的收益率分布

偏度一般用來衡量收益率概率分布的偏斜方向和偏斜程度。如圖1所示，實曲線C與虛曲線D是期望值相同的兩個概率分布，但其偏度不同。實曲線C的偏度大于0，

左尾薄而右尾厚，低收益率發生的概率較小，而高收益率出現的機會較大，這是令投資者滿意的。而虛曲線D的偏度小于0，左尾厚而右尾薄，低收益率發生的概率較大，而高收益率出現的幾率較小，這是投資者所不希望的。

正態分布是無偏分布，其偏度為0。但大量研究表明，投資組合的收益率不服從正態分布，而是呈現“尖峰厚尾”的形狀。收益率概率分布的“左尾”表示實際收益率低于預期收益率的概率，是投資者面臨的真正風險。因此，用偏度大于等于0來控制風險，既可以從整體上減少低收益率發生的概率，同時增加高收益率發生的幾率，符合投資者的心理。

要使組合收益率的偏度大于等于0，等價于使組合收益率的三階矩大于等于0，即

（3）投資比例和非負約束。組合中所有資產投資比例之和應等于 1，即

同時，組合中所有資產通常不允許賣空，即：

（三）模型建立 綜合（4）-（8）式，可以建立均值和偏度約束下CVaR最小的投資組合優化模型，即：

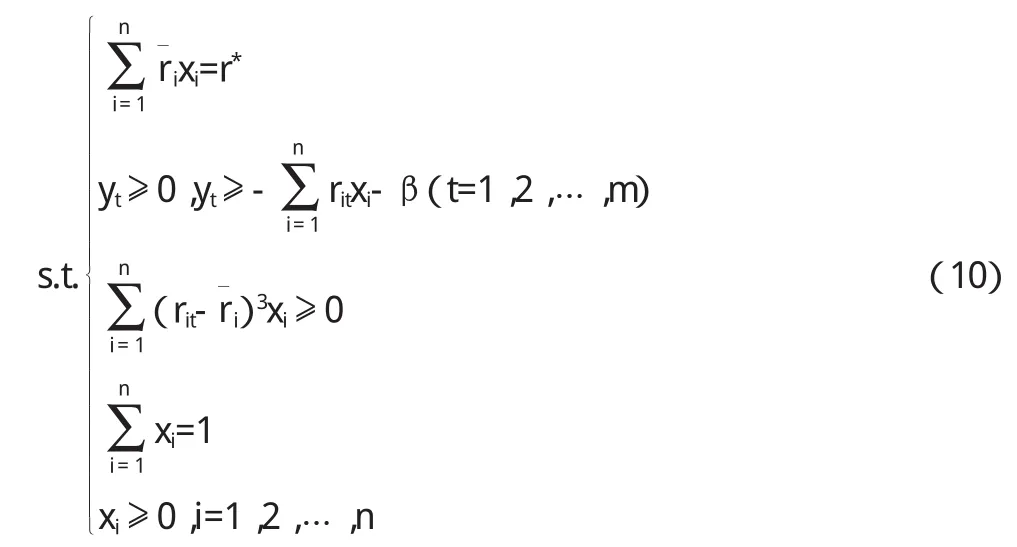
岳瑞峰等（2003）證明了在求解優化問題時將CVaR加以離散化和線性化處理后最優解不變，因此，（10）式中的模型與（9）式中的模型有相同的最優解。對（10）式中的模型進行求解后，目標函數值就是CVaR值，值就是VaR值。

由此可見，對CVaR加以離散化和線性化處理，不僅降低了優化模型的求解難度，而且在求解CVaR的同時順便得到VaR。同時，此模型不需要假定組合收益率服從某一具體分布就能求出投資比例，這使模型的適用范圍進一步拓寬，模型的實用價值也得以提升。

（四）模型特色 首先，在傳統的均值-CVaR模型中，引入偏度大于等于0的約束，既可以減少低收益率發生的概率，同時也增加高收益率出現的機會，進而降低了投資組合的風險，提高了模型的合理性。其次，對CVaR作離散化和線性化處理，將模型轉化為一般的數學規劃問題，不僅降低了模型的求解難度，而且使模型適用于求解任何形式的投資組合問題，提升了模型的實用性。

三、實證分析

（一）數據收集與統計分析 為分散組合風險，從我國滬深兩市不同行業隨機選取10只股票，時間從2012年1月6日到2012年7月6日，采集每周末的股票收盤價，使用表達式 計算股票周收益率，其中Pi，t和Pi，t-1分別表示第i只股票第t周和第t-1周的周末收盤價。通過計算可以獲得25周的數據，樣本描述性統計結果見表1：

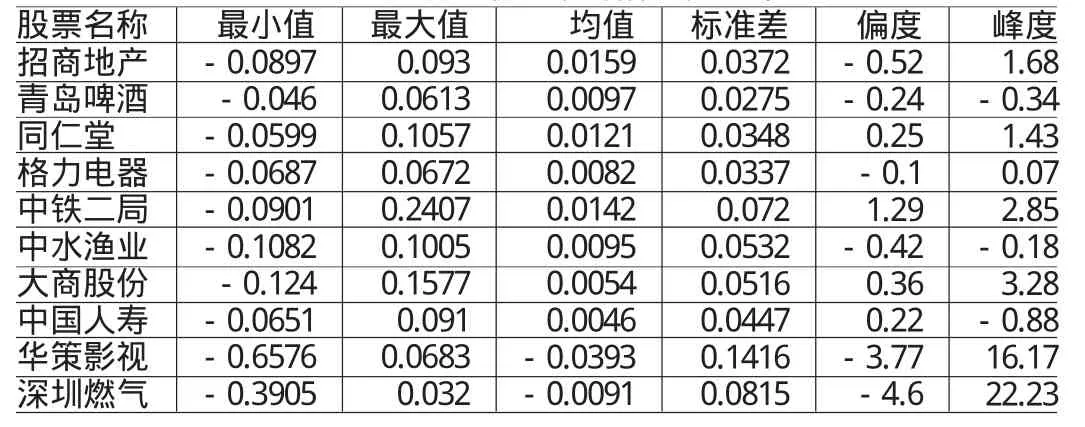
表1 10只股票收益率的描述性統計

由表1可知，10只股票收益率的偏度和峰度均不為0，不符合正態分布。其中，華策影視和深圳燃氣這兩只股票收益率的偏度分別為-3.77和-4.6，峰度分別高達16.17和22.23，其分布明顯帶有“尖峰厚尾”，發生極端損失的可能性較大。如果對負偏度產生的風險不予考慮，投資者遭受較大損失的可能性就會上升。

（二）模型求解與分析 將m=25，n=10等數據代入（10）式模型中，置信水平θ取95%，建立優化模型，并利用數學軟件MATLAB進行求解，計算結果如表2所示。由表2可以看出：在給定三種不同期望收益率下，投資的股票種類保持不變，始終為青島啤酒、格力電器、大商股份、中國人壽和深圳燃氣這五只股票，只是投資的比例有所調整。當周期望收益率設定為0.55%，投資者承擔的風險值CVaR和VaR分別為3.55%和4.17%，這意味著有95%的把握可以保證，上述五只股票的組合收益率在未來一周內，因市場波動而導致的正常損失不超過3.55%，極端損失不超過4.17%。同時也不難發現，在三種不同期望收益率下，CVaR值比VaR值均要大，這說明風險度量方法CVaR比VaR更能捕捉投資組合所面臨的極端風險。伴隨著期望收益率逐步提高，VaR和CVaR也同時增高，這表明投資者要求的報酬越高，承擔的風險也相應越高。

表2 模型的求解結果

四、結論

首先，本文使用組合收益率偏度大于等于零控制重大損失發生的概率，在既定的期望收益率水平下使組合的風險值CVaR最小，構建了均值和偏度約束下CVaR最小的投資組合優化模型，并利用股票市場數據對模型進行實證檢驗。其次，在傳統的均值-CVaR模型的基礎上引入偏度大于等于零約束，既減少低收益率發生的概率，同時也增大高收益率出現的機會，進而降低了投資組合的風險，提高了投資的合理性。最后，對CVaR進行離散化和線性化處理，不僅降低了模型的求解難度，而且使模型適用于任何概率分布的投資組合問題，提高了模型的實用性。

［1］ 張樹斌、白隨平、姚立：《含有交易成本的均值-方差-偏度資產組合優化模型》，《數學的實踐與認識》2004年第2期。

［2］ 高岳林、孫瀅、安曉會：《基于偏度的多期組合投資調整模型》，《商業研究》2010年第2期。

［3］ 遲國泰、遲楓、閆達文：《貸款組合的“均值-方差-偏度”三因素優化模型》，《運籌與管理》2009年第4期。

［4］ 林東旭、鞏前錦：《正態條件下均值-CVaR有效前沿的研究》，《管理科學》2004年第3期。

［5］ 肖甲山：《CVaR風險度量方法及在投資組合優化中的應用研究》，中南大學出版社2008版。

［6］ 吳灝文：《基于高階風險防范的銀行資產負債組合優化模型研究》，大連理工大學出版社2011版。

［7］ 岳瑞峰、李振東、楊曉萍：《風險管理的CVaR方法及其簡化模型》，《河北省科學院學報》2003年第3期。