一種新穎的第二類Stirling數公式證明

李新社， 姚俊萍

（西安高新技術研究所，陜西西安 710025）

0 引 言

Stirling數在資源分配、微積分應用、有限集合劃分等方面都有著廣泛的應用，所以諸多學者在論文或編著中都研究和討論Stirling數，但由于Stirling數復雜，計算公式難以推導，所以證明過程難以掌握接受。文獻［1］通過7個引理和數學歸納法完成了第二類Stirling數公式的證明，篇幅長達兩個版面，推導變化異常復雜；文獻［2］通過不完全歸納法進行猜想Stirling數公式，然后，通過大量的組合計算變換完成了第二類Stirling數公式的證明，關鍵是猜想的邏輯難以論述，不易閱讀、理解和掌握；文獻［3］給出了一些特殊情況下的Stirling數計算公式，缺乏普遍性，難以推廣使用；文獻［4］通過數學歸納法完成了第二類Stirling數公式的證明，但證明過程長，而且只回答了公式的正確性，未回答公式的模型構造過程。文中根據函數定義、滿射函數特性、容斥原理、逐步淘汰原理、排列組合理論等，討論分析了滿射函數與有限集合劃分的關系，基于逐步淘汰原理給出了有限集合間滿射函數個數的計算公式，最后由滿射函數個數計算公式推導出含有m個元素的有限集合劃分成n個非空子集的種類數計算公式，從而完成了第二類Stirling數公式的一個既簡單又易接受的證明過程。

1 基本概念與基本原理

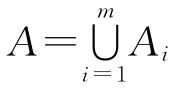
定理1 設π是非空集合A上的劃分，R是A上的等價關系，那么π誘導出R當且僅當R誘導出π。

定理2（容斥原理） 設A1，A2，…，An為有限集合，則

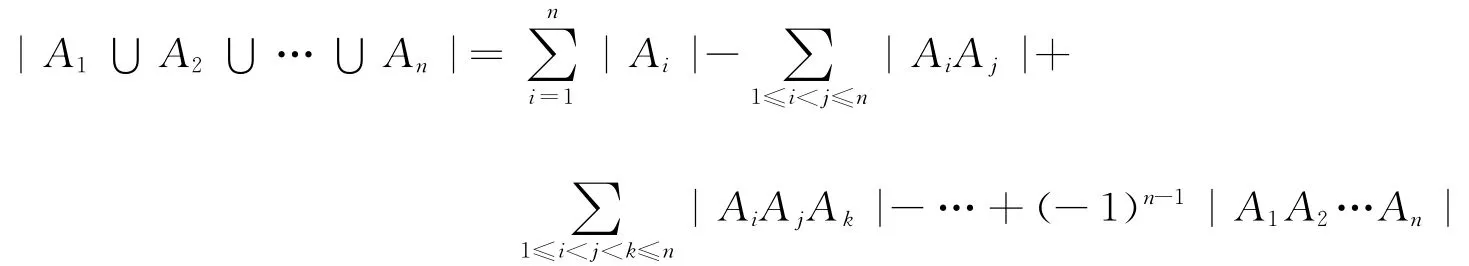
定理3（逐步淘汰原理） 設A1，A2，…，An為有限集合S的子集，則

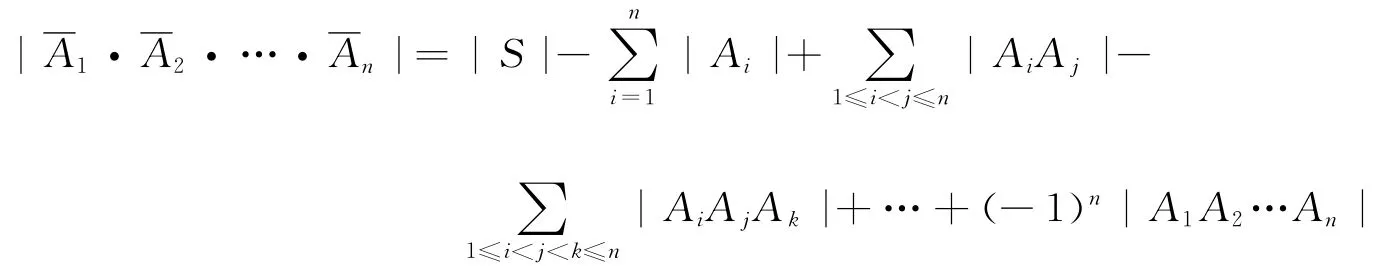
定義2 設A，B是兩個集合，如果按照某種對應法則f，對于集合A中的任何一個元素，在集合B中都有唯一的元素和它對應，這樣的對應叫作從集合A到集合B的映射。記作：f：A→B。

定義3 設f是A到B的一個映射，若對B中的每一個元素y，都存在x∈A使得y＝f（x），則稱f是A到B的一個滿射。

根據文獻［6-7］，Stirling數的本質在于求解有多少種方法可將一個含有m個元素的有限集合劃分成n個非空的子集，記為S（m，n）。根據這一含義顯然有

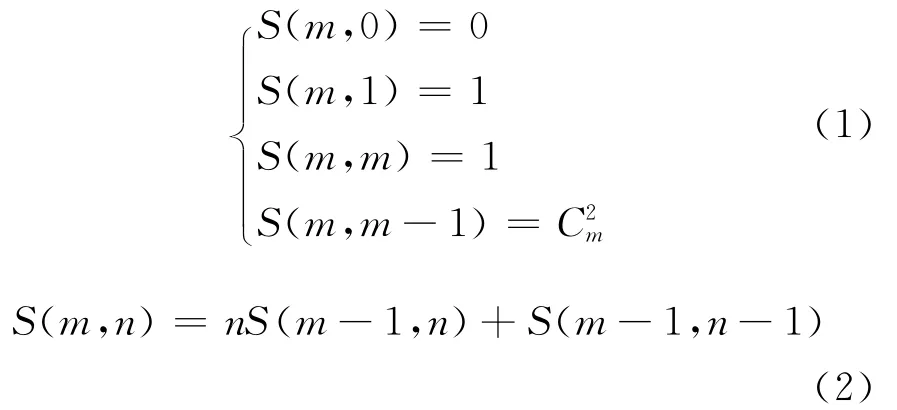
S（m，n）數列通項計算公式為

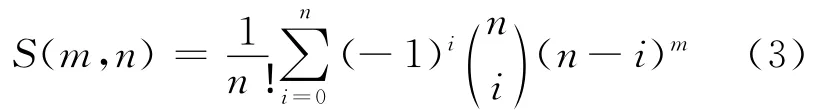
現在的問題是上面這個通項計算公式是否正確？如何得來？正如引言所論述，文獻［1-4］的作者和其他一些國內外學者都給出了一些研究成果，但推導過程復雜，難以理解和掌握。下面基于定義1、定義2、定義3、定理1、定理2、定理3等展開研究。

2 有限集合劃分與有限集合間滿射函數的關系

設f：A→B為A到B的任意一個滿射函數，其中，｜A｜＝m，｜B｜＝n，m＞n，規定A上的二元關系R為

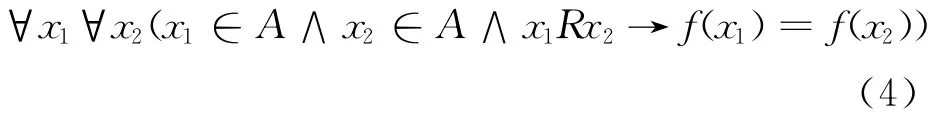
不難證明R具有自反性、對稱性和傳遞性，是A上的一個等價關系。這樣由一個滿射函數就確定了一個等價關系，而基于這個等價關系正好將A可劃分成n個非空子集。又根據有限集合上的等價關系與有限集合的劃分是一一對應的（定理1），所以滿射函數與劃分之間有對應關系，但注意到等價關系定義中強調的是函數值相同，未強調對應的具體值，也就是說函數值之間可以互換并不改變劃分結果，因此，根據函數定義和排列組合原理可以得出n！個函數對應一個劃分。換句話說，如果求得A到B的滿射函數個數，就可求得將一個含有m個元素的有限集合劃分成n個非空子集的方法數。

3 有限集合間滿射函數個數的計算公式

同上，仍然設f：A→B為A到B的任意一個滿射函數，｜A｜＝m，｜B｜＝n，m＞n。

根據滿射函數定義，B中每個元素都要被映射到，直接求出所有滿射函數個數有困難。但從A到B的所有函數中除去B中至少有一個元素未被映射到的函數，就可得到A到B的所有滿射函數。而這正是容斥原理（定理2）和逐步淘汰原理（定理3）解決問題的思路和方法。

首先根據定義2易知，A與B之間可構造的函數有nm個，其次B中有一個元素未被映射到的函數個數為（n－1）m個；B中有2個元素未被映射到的函數個數為（n－2）m個；…；B中有i個元素未被映射到的函數個數為（n－i）m個；B中元素都未被映射到的函數個數顯然為0，即（n－n）m。由定理3得可構造的滿射函數個數為

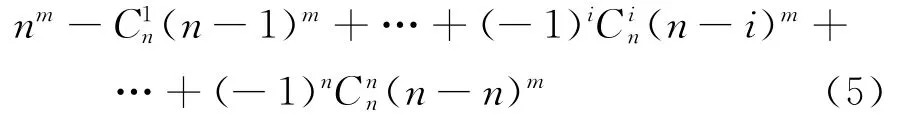
即

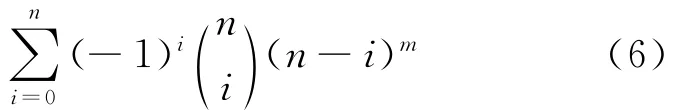
4 第二類Stirling數公式與驗證

根據“2”和“3”的討論，立即可以得出

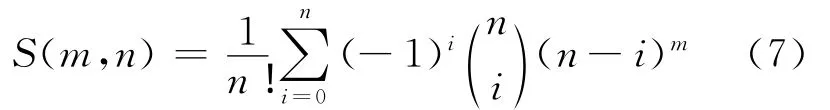
對于得出的公式，顯然S（m，0）＝0，S（m，1）＝1，S（m，m）＝1，S（m，m－1）＝是成立的，符合Stirling數的含義。

至于S（m，n）＝nS（m－1，n）＋S（m－1，n－ 1），結合

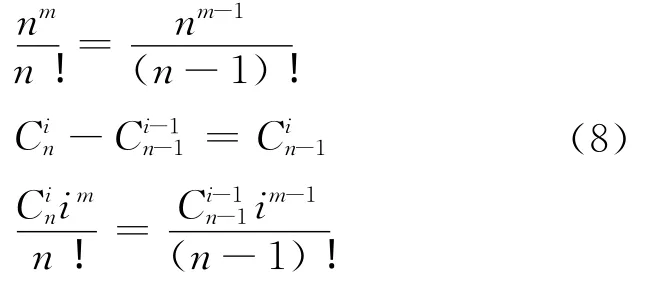
也可驗證是成立的。

5 結 語

通過滿射函數、等價關系、劃分、逐步淘汰原理等的相互聯系，給出了第二類Stirling數公式證明過程。該證明過程不僅揭示了第二類Stirling數公式的來源，而且從另一個方面回答了其正確性，有助于對第二類Stirling數本質含義的理解和大力推廣使用。

［1］ 任逸.第二類Stirling數的一個計算公式及其證明［J］.數學通報，2008，47（3）：59-60.

［2］ 楊雅琴.第二類Stirling數計算公式的一種證明［J］.青島科技大學學報：自然科學版，2009，30（4）：91-93.

［3］ 王紅，楊雅琴，王艷輝.第一類Stirling數和第二類Stirling數的關系式［J］.高師理科學刊，2008，28（6）：37-39.

［4］ 吳學澄.計算第二類Stirling數的公式的證明［J］.東南大學學報：自然科學版，1987，17（3）：159-161.

［5］ 方世昌.離散數學［M］.西安：西安電子科技大學出版社，2005.

［6］ 盧開澄.組合數學［M］.北京：清華大學出版社，1999.

［7］ Danie I A Cohen.Basic techniques of combinatorial theory［M］.［S.l.］：John Wiley ＆Sons Inc，1979：107-119.