時變競爭種群模型的反射函數及其周期解
潘穎昕, 劉文俊
(1.如皋高等師范學校 數理與信息技術系, 江蘇 如皋 226500;2.揚州大學 數學科學學院, 江蘇 揚州 225002)
我們知道時變競爭種群模型可以用來刻畫生物種群的變化規律,對于自治的時變競爭種群模型,通過廣大數學家的深入研究已取得了豐富的成果[1-4].然而對于非自治的情形,由于模型的復雜性,往往很困難.在本文中我們首次應用MIRONENKO[5-7]反射函數法來研究時變競爭種群模型周期解的形態,由于方法的新穎,因此必將得出許多新的成果.為方便起見,我們首先簡單介紹有關反射函數的概念.
1 基本概念及基本定理
假設微分系統
x′=X(t,x),t∈R,x∈Rn
(1)
右端連續可微,滿足解的存在唯一性定理的條件.
定義1[5]設F(t,x)為n維連續可微的向量函數,并滿足
(2)
則稱F(t,x)為微分系統(1)的反射函數.
引理1[5]若X(t+2ω)=X(t),且F(t,x)為式(1)的反射函數,則式(1)的Pincaré映射為T(x)=F(-ω,x),從而式(1)在[-ω,ω]有定義的解x=φ(t;-ω,x0)為2ω-周期解當且僅當F(-ω,x0)=x0.
定義2[5]若函數F(t,x)滿足F(-t,F(t,x))=F(0,x),則稱微分系統
x′=-(Fx(t,x)+E)-1Ft(t,x)
(3)
為以F(t,x)為反射函數的簡單微分系統.由文獻[5]知,微分系統
(4)
與微分系統(3)具有相同的反射函數F(t,x),從而當它們為t的2ω-周期系統時,這些微分系統(4)的周期解的形態相同,這里R(t,x)為任意連續可微函數.
考慮時變競爭種群模型
(5)
這里ai(t),i=0,1,2,bj(t),j=0,1,2,3,4,5為連續可微函數,并保證微分系統(5)的初值問題的解存在唯一.由于a2(t)≡0時,系統(5)為可積系統,從而其解的形態是已知的,所以這里假設a2(t)不恒為零.
假設F(t,x,y)=(F1(t,x,y),F2(t,x,y,))T為微分系統(5)的反射函數.我們首先討論當微分系統(5)為以F(t,x,y)為反射函數的簡單微分系統時,函數F(t,x,y)的結構形式,接著討論微分系統(5)具有某些函數為反射函數的充分條件,并應用所得結論討論微分系統(5)的周期解的形態.
2 主要結果
若微分系統(5)為簡單系統,則由文獻[5]得
(6)
(7)
這里及下文中記

F1∶=F1(t,x,y),F2∶=F2(t,x,y).
由假設a2(t)≠0,則由式(6)得
(8)
將式(8)代入式(7)得
(9)
式中
引理2若微分系統(5)為以F(t,x,y)為反射函數的簡單微分系統且A6≠0,則F(t,x,y)為x,y的有理分式.
證明因為A6≠0,所以式(9)可改寫為
(10)
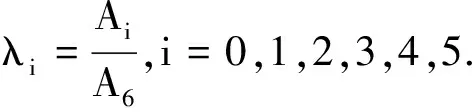
(11)
式中
B0=Dλ0+λ1P,B1=Dλ1-2λ2P,B2=Dλ2-3λ3P,
B3=Dλ3-4λ4P,B4=Dλ4-5λ5P,B5=Dλ5-6P,
Dλi=λit+λixP+λiyQ,i=0,1,2,3,4,5.
由于λ5為t的函數,而P為關于t,x,y的函數,故B5≠0,則式(11)可改寫為
(12)

(13)
式中
C0=λ0-λ5μ0+μ0μ4,C1=λ1-λ5μ1+μ1μ4-μ0,C2=λ2-λ5μ2+μ2μ4-μ1,
情形1若C4≠0,則由式(13)得
(14)
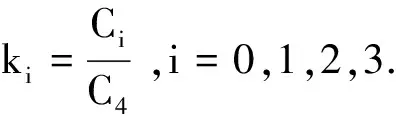
(15)
式中
D0=Dk0-k1P,D1=Dk1-2k2P,D2=Dk2-3k3P,D3=Dk3-4P,
Dki=kit+kixP+kiyQ,i=0,1,2,3.
1)若D3≠0,則式(15)可改寫為
(16)
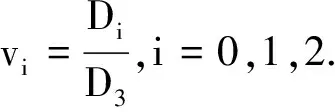
(17)
式中
(1)若E2≠0,則由式(17)得
(18)
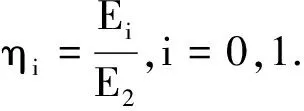
G0+G1F1=0
(19)
式中
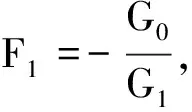
(b)若G1≡0,則由式(19)得G0≡0,整理得
(20)
又對方程(16)作變換F1=Z-v2可得
(21)
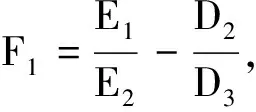
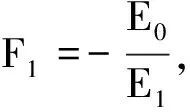
(3)若E2≡0,E1≡0則由式(17)得E0≡0,整理得
(22)
對式(14)作變換F1=G-k3可得
(23)
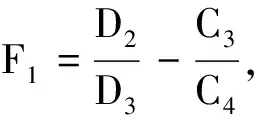
2)若D3≡0,D2≠0或D3≡0,D2≡0,D1≠0,易得定理結論成立.
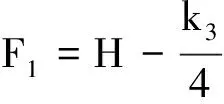
δ0+δ1H+δ2H2+H4=0
(24)
式中
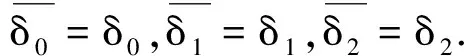
因此,將式(24)中t用-t替代可得
(25)
情形2若C4≡0,與情形Ⅰ同理可得定理的結論成立.
與引理2同理可得
引理3若微分系統(5)為以F(t,x,y)為反射函數的簡單微分系統且A6≡0,則F(t,x,y)為x,y的有理分式.
由引理2及引理3可得
定理1若微分系統(5)為以F(t,x,y)為反射函數的簡單微分系統,則F(t,x,y)為x,y的有理分式.
下面我們討論微分系統(5)何時具有線性和一次有理分式形式的反射函數.
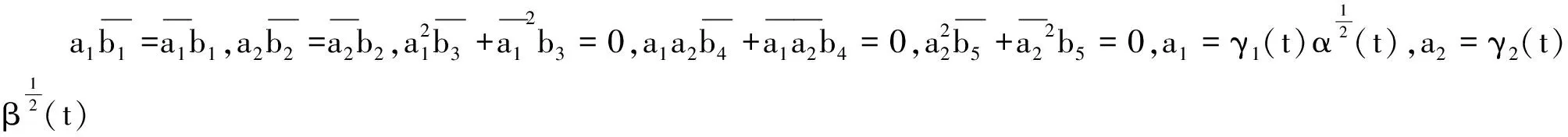
F(t,x,y)=(α(t)x,β(t)y)T
(26)
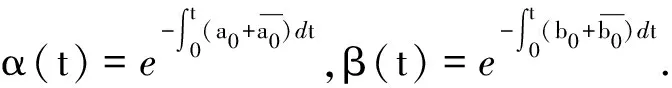
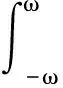
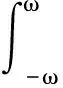
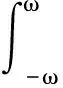
證明在定理的條件下容易驗證函數(26)為Cauchy問題(2)的解,從而函數(26)為微分系統(5)的反射函數.再由引理1及文獻[5]可得定理的結論成立.
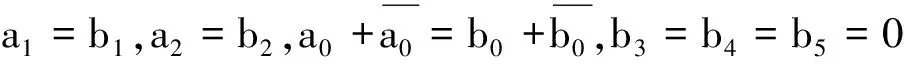
(27)
式中
此外,若微分系統(5)為t的2ω-周期系統,則
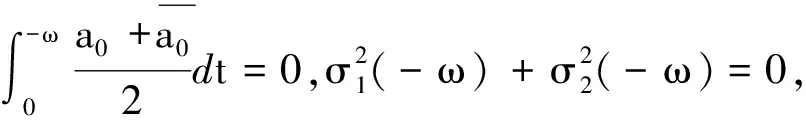
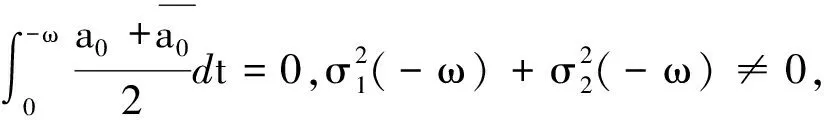

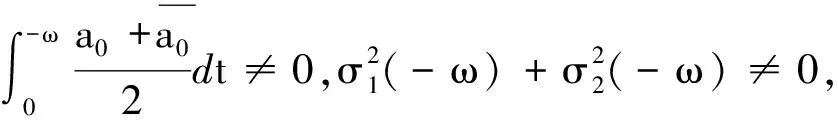
證明在定理的條件下容易驗證函數(27)為Cauchy問題(2)的解,從而函數(27)為微分系統(5)的反射函數.當微分系統(5)為2ω-周期系統時,由文獻[5]知,此時該周期系統的Poincaré映射為T(x,y)=F(-ω,x,y),由引理1可得該定理的結論成立.
例1微分系統
以F(t,x,y)=(x,y)T為反射函數,由于F(-π,x,y)=(x,y)T,故該微分系統在[-π,π]上有定義的解皆為2π-周期解.
例2微分系統
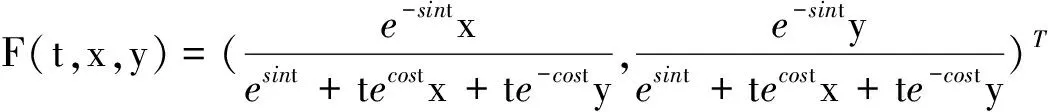
[1] 陳蘭蓀,宋新宇,陸征一.數學生態學模型與研究方法[M].四川:四川科學技術出版社,2003.
[2] Takeuchi Y. Global dynamical properties of Lotka-Volterra systems[M]. [S.l.]:World Scientific Publishing Company,1996.
[3] Zhou Z X. On the Poincar mapping and periodic solutions of nonautonomous differential system [J]. Commun Pure Appl Anal, 2007, 60(2): 541-547.
[4] Zhou Z X. The structure of reflective function of polynomial differential systems [J]. Nonlinear Anal, 2009, 71(1-2):391-398.
[5] Mironenko V I. The reflecting function and research of high-dimensional differential systems[M]. Belarus: Gomel University Press,2004.
[6] Mironenko V I, Mironenko V V. Time symmetries and in-period transformations[J]. Applied Math Letters, 2011, 24(10):1721-1723.
[7] Mironenko V I, Mironenko V V.How to construct equivalent differential systems [J]. Applied Math Letters, 2009, 22(9):1356-1359.

